Финансовые данные не только флуктуируют во времени, но и являются многомерными.
Из наблюдений за несколькими факторами рынка важно увидеть момент формирования тенденции рынка, необходимо следить за поведением различных игроков, привлекать дополнительную информацию, т.е. наблюдать рынок в многомерном пространстве.
В системе STATISTICA имеются широкие возможности анализа многомерных данных: канонический анализ, дисперсионный анализ, множественная регрессия, многомерное шкалирование, кластерный анализ, дискриминантный анализ, факторный анализ и его новейшее развитие — методы структурного исследования, — SEPАTH.
Классической задачей канонического анализа является построение такой линейной комбинации индексов производства, которая позволяет наиболее точно предсказать общий индекс цен; дискриминантный анализ позволяет классифицировать игроков на бирже или использоваться при назначении кредитных ставок тем или иным клиентам.
Следующий пример работы в модуле многомерного шкалирования является типичным для диалога в других модулях.
Предположим, вы имеете несколько типов акций и просите оценить экспертов степень их близости, например, в 10 бальной шкале. В итоге располагаете следующей матрицей:
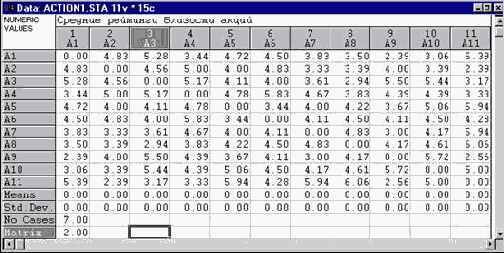
Такого рода матрицы называют матрицами сходства.
Чем выше сходство, тем больший рейтинг выставляет эксперт паре акций, например, степень близости акций А7 и А1 имеет рейтинг 3.83, а акций А7 и А10 рейтинг 5.91. Экспертов несколько, их показания усредняются. Каждый из них работает, т.е. выставляет рейтинги в соответствии со своими собственными представлениями. Вопрос состоит в том, можно ли таким образом получить объективное знание и на основании его рационально строить стратегию своих действий?
Очевидно, глядя на эту матрицу, трудно понять, насколько близки те или иные акции в общей совокупности. Конечно, хотелось бы рассмотреть эти данные на общем плане, например, представить их на плоскости в естественно интерпретируемых шкалах. Эту задачу можно решить в модуле многомерное шкалирование.
Содержание раздела
