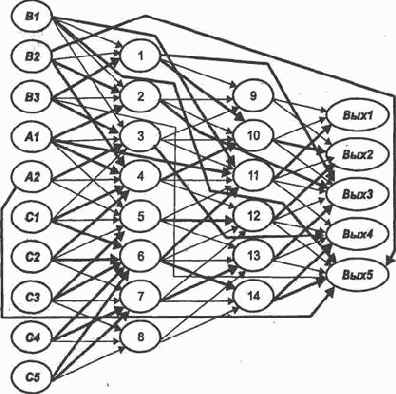
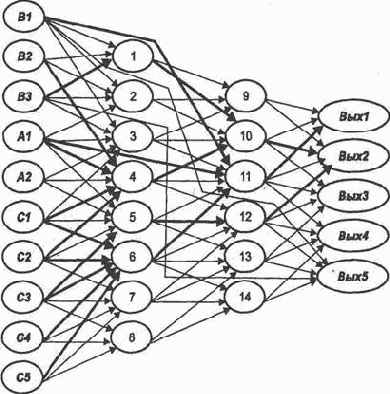
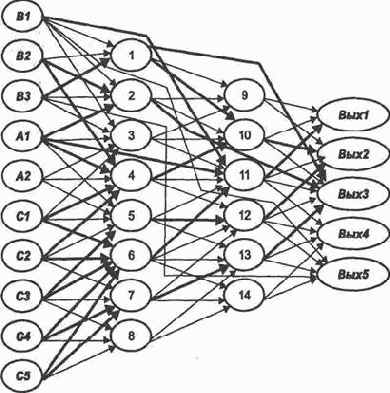
Выберем нейросеть, отражающую все особенности, необходимые для построения алгоритма трассировки, и возьмем тот же пример, который выглядит теперь следующим образом:
Задавая обобщенный эталон на входе, например, из тех, что приведены выше, необходимо наиболее рациональным образом построить пересекающиеся пути возбуждений, ведущие от каждого возбужденного входного нейрона к соответствующему нейрону выходного слоя. Пути должны быть максимально объединены, совмещены согласно стратегии слияния и общего выхода.
Ори этом разрабатывается эвристический алгоритм, с минимальным использованием ресурсов сети — ее нейронов и связей, а также с минимальным развитием, если связей недостаточно.
Пусть выбрана нейросеть (рис. 3.1), где первоначально заданные связи обозначены тонкими стрелками. Строим соответствующую матрицу следования S и в ней транзитивные связи (рис. 3.2). Проверяем, все ли нейроны выходного слоя достижимы из любого нейрона входного слоя? Если нет, считаем, что сеть составлена некорректно.
Из нейрона В\ не исходит ни одной статической цепочки, заканчивающейся нейроном Вых5, в связи с тем, что в строке, соответствующей нейрону Вых5, нет даже транзитивной связи в столбце, соответствующем нейрону В\. Это относится и к нейрону В3.
Введем непосредственные синапсические связи В1
3.2 — весами элемента матрицы.
Сформируем (см. подразд. 2.5) статический путь возбуждения [В1,А1, С1, СЗ, С4, С5]
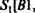
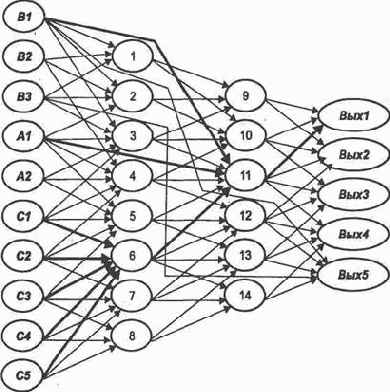
Вых\\ (рис. 3.3, а). Имитируя прокладываемые пути возбуждений, первоначально присваиваем нейронам входного слоя, отображенным нулевыми строками этой матрицы, признак «возбужден».
Найдем входы матрицы
Рис. 3.3. Матрица следования при обучении первому эталону:
а — общий вид; б — первый шаг преобразования матрицы следования;
в — после исключения нейронов В1,А1, и 6;
г — после исключения «невозбужденных» входов
Присвоим нейрону 6 признак «возбужден», а также значение
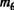
Исключим из матрицы
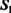
Вновь выделим столбцы, соответствующие «возбужденным» входам матрицы, т. е. нейронам В\, А\, 6. Находим строку в выделенной совокупности столбцов с максимальным числом нулей. Строка соответствует нейрону 11. Заменяем в этой строке нули единицами, т. е. максимально увеличиваем веса. Присваиваем нейрону 11 признак «возбужден» и значение
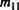
Последовательное исключение сверху вниз динамически учитывает появление таких нейронов и гарантирует полное исключение за один проход. Матрица
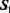
Теперь в первом столбце имеется единственная строка с нулем, соответствующая нейрону Вых\. Изменим нуль на единицу, окончательно получим возможный динамический путь возбуждения по заданному эталону.
Изменения отразим в матрице S.
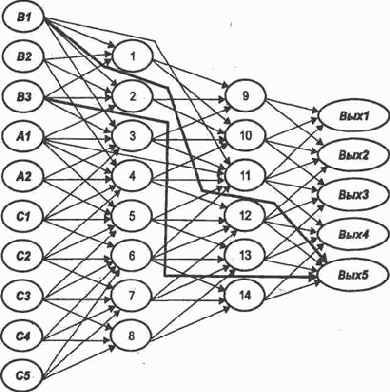
Не будем приводить новый вид матрицы следования S, а на изображении самой сети (рис. 3.4) выделим построенную трассу (опорный или динамический путь возбуждения по предполагаемому эталону).
В результате имеем сеть, обученную реакции на эталон одной комбинации событий.
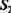
Составим обобщенный эталон ситуации {А\, В2, 53, С\, С2, СЗ}, требующий решения R2. Свяжем это решение с нейроном Вых2.
Вых2]
По сети, представленной на рис. 3.4, или по матрице (см. рис. 3.2), построим с учетом частичного обучения матрицу статического пути возбуждения(рис. 3.5).
На нейроне 6 ранее суммировалось возбуждение пяти нейронов: С1,С2, СЗ, С4, С5. Таким образом, и соответствующая строка матрицы S содержит пять единиц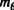 
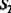
Исключим из данной матрицы строки и столбцы, соответствующие нейронам 6 и 11. Матрица примет вид, приведенный на рис. 3.6.
Объединим столбцы множества входов матрицы, обладающих признаком «возбужден», в данном случае первые шесть столбцов. Найдем в них первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 4.
Изменим в ней все нули на единицы, положим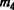 
Исключим из матрицы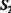 
Вновь объединим столбцы множества входов, обладающих признаком «возбужден», соответствующие нейронам ВЗ, С3, 4. В совокупности столбцов выберем первую строку, содержащую максимальное число нулей, — строку, соответствующую нейрону 1.
Заменим нуль на единицу, положим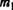 
Исключим из матрицы строку и столбец, соответствующие нейрону ВЗ, передавшему энергию возбуждения нейрону 1, а также исключим строки и столбцы, соответствующие образовавшимся входам — «не возбужденным» нейронам 2 и 3.
В столбцах, соответствующих нейронам — входам с признаком «возбужден», найдем строку с наибольшим числом нулей. Такая строка соответствует нейрону 10. Заменим нули на единицы, присвоим нейрону признак «возбужден», полагаем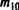 
В матрице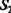 
Нейрон 9, не обладающий признаком «возбужден», образует вход матрицы. Исключим соответствующие ему строку и столбец.
Выделим столбцы, соответствующие нейронам С3 и 10, и в них находим строку с максимальным числом нулей. Такая строка соответствует нейрону 5. Заменяем в ней нуль единицей, полагаем 
Исключим из матрицы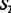 
В совокупности выделенных столбцов, соответствующих нейронам 5 и 10, строка, соответствующая нейрону 12, имеет единственный нуль. Заменим его на единицу, присвоим нейрону 12 признак «возбужден», положим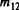 
строку истолбец, соответствующие нейрону 5. И наконец, на последнем шаге, заменив нули в строке, соответствующей нейрону Вых2, единицами, окончательно получим искомый путь возбуждения (рис. 3.7).
Обучим сеть ситуации, требующей решения R3. Пусть этому решению соответствует нейрон ВыхЗ. Матрица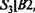 
изображен на рис. 3.8, б. Присвоим всем нейронам, образующим входы матрицы, признак «возбужден». Выделим и объединим столбцы, соответствующие входам матрицы Однако вследствие ранее выполненных построений — в результате частичного обучения — появляются новые особенности. Поэтому расширим последующие действия.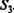 
В выделенных столбцах найдем строку, содержащую максимальное число единиц.
Строка представляет тот нейрон, который приобрел энергию возбуждения одного или нескольких нейронов, образующих входы матрицы. Эти нейроны могут быть исключены из рассмотрения. Так, нейрон 1 возбужден единственным нейроном, принадлежащим текущему множеству входов матрицы, — нейроном В3, который может быть исключен из рассмотрения. Матрица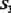 
, уничтожив веса в его строке.
Вновь найдем множество входов матрицы и выделим соответствующие столбцы. Отыщем строку, содержащую единицы в этих и только этих столбцах. Таковых больше нет.
Рис. З.8. Шаги преобразования матрицы следования для обучения третьему эталону: а — общий вид; б — матрица следования после исключения неиспользованных нейронов.
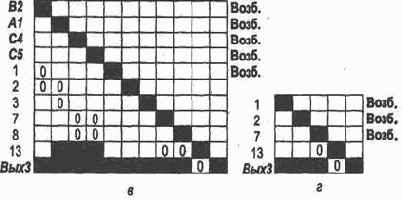
Тогда найдем строку, содержащую максимальное число нулей. Первая такая строка соответствует нейрону 2. Заменим нули единицами, положим = 2, исключим нейроны B2 и A1 из рассмотрения, присвоим нейрону 2 признак «возбужден». Отразим сделанные изменения весов в матрице S.
Исключим входы, не обладающие признаком «возбужден», — нейроны 3 и 5.
Выделим столбцы, соответствующие входам. В них нет строк, содержащих единицы. Тогда найдем строку, содержащую максимальное число нулей. Такая строка соответствует нейрону 7. Заменим нули (в выделенной совокупности столбцов) на единицы, положим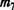
Выделим столбцы, соответствующие «возбужденным» входам и не находим строк, содержащих единицы. Тогда найдем первую строку с максимальным числом нулей. Это строка, соответствующая нейрону 13. Заменим нуль на единицу, нейрону 13 присвоим признак «возбужден», полагаем
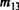
Выделим столбцы, соответствующие множеству «возбужденных» входов. В них нет строки с единицами, но единственная строка с максимальным числом нулей соответствует нейрону ВыхЗ. Заменим нуль на единицу. Однако статус этого нейрона особый, и значение т, как и признак «возбужден», ему не присваивается.
Исключим нейрон 13 из рассмотрения.
Выделим множество столбцов, соответствующих «возбужденным» входам, т. е. нейронам 1 и 2. Ищем в этих столбцах строку с единицами, затем с максимальным числом нулей, но таковых нет. Следовательно, необходимо ввести дополнительные связи. Для этого в каждом столбце найдем первую сверху транзитивную связь и заменим ее на единицу. Тогда данная сеть дополнится динамическими цепочками возбуждения 1
ВыхЗ.
Построение трассы решения R3 закончено, и сеть имеет вид, представленный на рис. 3.9.
Приступим к обучению следующему обобщенному эталону — решению А2 & В3 & С1 & С2 & С3 & С4 & С5 
[В3, А2, С1, C2, С3, C4, C5 
Исключим из рассмотрения те нейроны, для которых количество единиц в строках меньше т. Такими нейронами являются 4 и 11. Матрица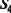 
Присвоим всем нейронам входам признак «возбужден». Выделим столбцы, соответствующие входам, это первые семь столбцов. Найдем строку с максимальным числом единиц в этих столбцах при отсутствии единиц в других. Строка соответствует нейрону 6. Теперь нейрон 6 представляет нейроны С\, С2, С3, С4, С5, передавшие ему энергию возбуждения. Присвоим ему признак «возбужден», исключим из рассмотрения перечисленные нейроны, матрица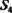 
Для «невозбужденных» нейронов исключим в матрице строки (и столбцы), число единиц в которых меньше т. Они соответствуют нейронам 5 и 7. Повторим этот щаг до полного исключения таких нейронов исключаются нейроны 12 и 13. Матрица примет вид, представленный на рис. 3.10, г. 
Исключим из рассмотрения множество «невозбужденных» входов. К таковым относится нейрон 8. Выделим множество столбцов, соответствующих входам матрицы. В их совокупности найдем первую строку с максимальным числом нулей (единиц нет во всей матрице). Такую строку образует нейрон 3. Нули в ней соответствуют нейронам ВЪ и А2. Исключим эти нейроны из рассмотрения, положим
Вновь выделим множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, найдем строку с максимальным количеством нулей, соответствующую нейрону 14. Заменим в ней нуль на единицу, положим 
Выделим множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, найдем строку с максимальным количеством нулей. Эта строка соответствует нейрону Вых4. Заменим в ней нуль на единицу. Поскольку это нейрон выходного слоя, не станем присваивать ему признак «возбужден» и значение т. Исключим нейрон 14 из рассмотрения. Вид матрицы представлен на рис. 3.10, е.
В этой матрице множество «возбужденных» входов представлено единственным нейроном 3. Однако в соответствующем ему столбце нет ни единичных, ни нулевых элементов. Введем в сеть дополнительную связь, найдя в этом столбце первую сверху транзитивную связь и положив ее вес равным единице. Эта связь порождает динамический путь возбуждения 3 
Теперь приступим к трассировке последнего пути возбуждения А2 & В1 & В2 & С1 & С2 & СЗ & С4 & С5 
На основе текущей матрицы S построим матрицу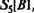 
Вых5] путем исключения «ненужных» строк и столбцов с сохранением транзитивных связей. Исключим из рассмотрения нейрон 4, для которого количество единиц в строке меньше 
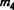
представлена на рис. 3.12, а.
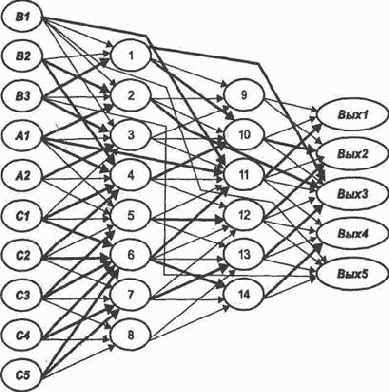
Присвоим всем входам признак «возбужден». Выделим столбцы, соответствующие «возбужденным» входам. В совокупности этих столбцов найдем строку, содержащую максимальное число единиц в этих и только этих столбцах. В данном случае такая строка соответствует нейрону 6. Присвоим ему признак «возбужден» и исключим из рассмотрения нейроны С1,..., С5.
Далее исключим из рассмотрения нейроны 5 и 7, так как в соответствующих строках отсутствуют единицы при отличных от нуля значениях т, после чего придется исключить по той же причине нейроны 12 и 13. Получившаяся матрица представлена на рис. 3.12, б.
Исключим из рассмотрения «невозбужденный» вход, соответствующий нейрону 8.
Выделим столбцы, соответствующие «возбужденным» входам, и в их совокупности найдем строку, содержащую наибольшее число единиц при отсутствии единиц в других столбцах. Строка соответствует нейрону 14. Исключим из рассмотрения нейрон 6, как передавший свое возбуждение нейрону 14, присвоим нейрону 14 признак «возбужден». Матрица примет вид, представленный на рис. 3.12, в.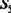 
Выделим столбцы входов, соответствующие «возбужденным» нейронам, и в их совокупности найдем строку, соответствующую нейрону выходного слоя Вых5, содержащую максимальное число нулей (строк с единицами больше нет). Заменим нули на единицы. Исключим нейроны В1 и 14 из рассмотрения. Отразим введенные изменения в матрице S. На рис. 3.12, г приведена полученная матрица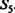 
Выделим множество столбцов — входов матрицы. В этих столбцах не находим строк, содержащих единицы, а также строк, содержащих нули. Тогда в каждый столбец занесем единицы на места транзитивных связей, т. е. введем связи В2 
Трассировка нейросети закончена. Окончательный ее вид представлен на рис. 3.13, где единичные веса соответствуют жирным стрелкам.
