В подразд. 2.9 указывалось, что любой предикат алгебры логики может быть записан в виде дизъюнктивной нормальной формы как дизъюнкция конъюнкций значений предиката и утверждений, принимающих значения ИСТИНА — ЛОЖЬ, а также их отрицаний. Поэтому будем считать, что каждый предикат системы, на основе которого строится нейронная сеть для принятия решений, представляет собой дизъюнкцию конъюнкций событий, приводящих к общему решению. Например, система предикатов (2.1) в записи на Алголе имеет вид:

Тогда трассировка нейросети заданной структуры по каждому предикату производится в два этапа. На первом этапе формируются термы — конъюнкции событий, за которыми закрепляются нейроны. Эти нейроны «собирают» возбуждение нейронов входного слоя. На втором этапе исключаются из рассмотрения нейроны входного слоя, на основе которых сформированы термы. Входным слоем нейронов становятся нейроны входного слоя сети, соответствующие событиям, не вошедшим в состав термов, а также нейроны, реализующие термы. Формируется связь этих нейронов с нейроном выходного слоя, закрепленным за решением.
Как ранее говорилось, для выполнения такой трассировки достаточно взять двухслойную сеть.
Однако в такой сети первоначально может быть недостаточно заданных связей, поэтому целесообразно дополнить сеть необходимыми связями. Ведь из сказанного выше следует, что могут понадобиться связи «через слой», т.е. возможен отход от традиционной «слоистости» сети.
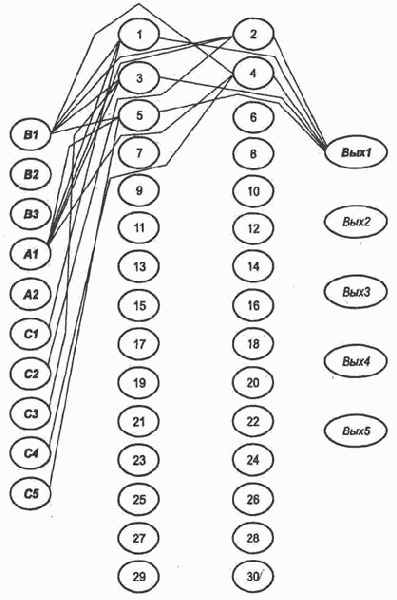
На рис. 3. 14 показана трассировка двухслойной сети, реализующей систему предикатов (3.2). Связи между слоями первоначально заданы по принципу «каждый с каждым». Выделены связи с весами, равными единице.
В дополнение к сказанному отметим следующее.
Если ситуация, приводящая к некоторому решению, поглощается обобщенным эталоном, приводящим к другому решению, то нейросеть не сводится к однослойной и дает неоднозначный ответ (см. подразд. 2.9). При этом правильное логическое описание системы принятия решений состоит из описания логических функций, каждая из которых представляет собой скобочную запись с единственным вхождением переменных. Трассировка должна производиться в соответствии с вложенностью скобок.
Таким образом, необходимо обобщение предлагаемого здесь алгоритма трассировки.
