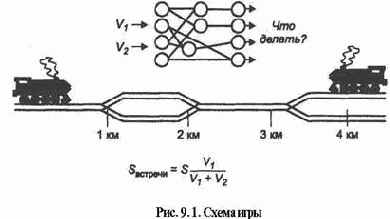
Построение обученной нейросети. Рассмотрим увлекательную детскую игру «железнодорожная рулетка», основанную на известной задаче о встрече. Помните: «Из пунктов А и В двигаются навстречу друг другу..»?
Начальник станции Кукуевка (ведущий) и начальник станции Пырловка одновременно выпускают навстречу друг другу два паровоза (рис. 9.1) со скоростью либо 60, либо 80 км/ч. Длина перегона составляет 4 км. Проблема заключается в том, что пути перегона то сходятся в один на протяжении одного километра, то расходятся. И тогда в зависимости от точки встречи со станции Кукуевка надо выслать на соответствующий километр либо линейного с приветственным флажком, либо линейного с подстилочной соломкой. Ситуация усложняется помехами при передаче данных, в связи с чем достоверность сообщения о скорости паровозов меньше единицы. Кроме того, необходимо учесть ожидаемые денежные затраты на единовременную добавку к пенсии линейных.
Начальник станции Кукуевка хочет добиться определенности по принципу «если — то», а в случае недостоверных данных — «на что это похоже, и что делать?».
Ясно, что без элементов искусственного интеллекта не обойтись. Необходимо что то похожее на табличный метод, но с автоматической интерполяцией, что то связанное с ассоциативным мышлением...
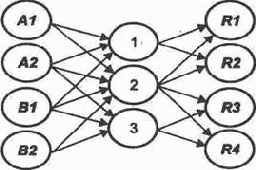
Представим себе все варианты будущего поведения нашей системы принятия решений для ее обучения. Графическая структура логического функционирования создаваемой системы приведена на рис. 9.2.
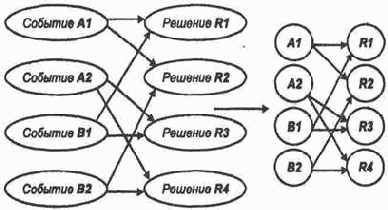
1. Скорость кукуевского паровоза — 60 км/ч (событие AY). Скорость пырловского паровоза — 60 км/ч (событие В\). Одновременное выполнение этих событий обозначим А1&B1. Тогда точка встречи находится как раз посредине перегона, что скорее всего требует помощи линейного с соломкой. Но возможен и другой исход за счет неточного определения скоростей. Тогда на всякий случай потребуется линейный с флажком. Решение, согласно которому оба линейных отправляются на границу второго и третьего километров, обозначим R1. С ним связаны расходы на единовременное пособие Ml.
2. Скорость кукуевского паровоза — 60 км/ч (событие АХ), скорость пырловского — 80 км/ч (событие B2). Выполняется условие АХ&В2. Тогда точка встречи находится на втором километре пути, и, следовательно, требуется решение R2: «Отправить линейного с флажком на второй километр!» В активе указанного линейного появляется сумма М2 условных единиц.
3. Скорость кукуевского паровоза 80 км/ч (событие А2), скорость пырловского — 60 км/ч (событие В\). Выполняется условие А2&В1. Тогда точка встречи находится на третьем километре пути, что требует сочувственного вмешательства линейного с соломкой (решение R3), с оплатой труда в М3 условных единиц.
4. Скорость кукуевского и пырловского паровозов — 80 км/ч (событие А2&В2), что ввиду высокой скорости перемещения линейных требует решения R4 с затратами М4.
А теперь оживим эту структуру, заставим ее действовать так же, как, по видимому, на логическом уровне действуют структуры нашего мозга. Представим себе, что на месте каждого овала (далее кружочка, см. рис. 9.2) действует нейроподобный элемент или просто нейрон. Нейроны рецепторы приходят в возбужденное состояние (подобно сетчатке глаза) в соответствии с той ситуацией, которая задана на входе системы. Рассмотрим, например, ситуацию А1&В2. Положим величины возбуждения нейронов А1 и B2 равными единице и запишем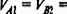
Подчеркнем тот факт, что возбуждение нейроноврецепторов осуществляется в результате ввода информации.
Для «принимающих» возбуждение нейронов (направление распространения сигналов возбуждения указано стрелками) в результате выполнения передаточной функции формируется величина возбуждения V.
Пусть в нашем случае эта функция имеет вид
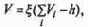
где i индекс нейрона, передающего свое возбуждение, h — порог.
Следует учесть, что функция 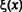
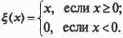
Положим А = 1 и рассчитаем величины возбуждения нейронов выходного слоя R\ — R4 для ситуации А\& В2:
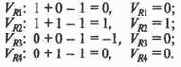
Таким образом, при точном знании ситуации получаем предусмотренное решение. Проверим, что наша сеть так же правильно работает и по остальным эталонам, по которым мы ее обучили, наметив направления распространения возбуждений от каждой исходной посылки к следствию.
Теперь поэкспериментируем.
Задавая события по принципу «да — нет», «1—0», мы предполагали булевский тип исходных данных. А что если обобщить тип исходных данных, допустив рассмотрение значений, интерпретируемых как достоверность? Или каких то других взаимных оценок, используемых людьми, не сведущими в теории вероятности и не знакомыми с понятием «полное множество событий»?
Например, в результате искажения информации начальник станции Кукуевка пребывает в раздумье: скорость пырловского паровоза равна не то 60 км/ч, не то 80 км/ч, но скорее всего 60 км/ч. Он по наитию набирает: А1 = 1, В1 = 0,7, В2 = 0,4. На какую ситуацию это похоже и какое решение принять?
Считаем:
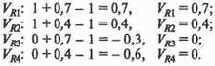
Мы видим, что максимальной величины возбуждения достиг нейрон R1, определивший главное решение. Но мы вправе учесть и решение R2 с меньшим приоритетом, дав линейному с флажком дополнительные указания. По известной формуле математического ожидания оценим, на сколько облегчится карман начальника станции Кукуевка:

Таким образом, сформирована уже обученная нейросеть.
А что если объединить решения R1 и R4, отличающиеся только скоростью передвижения линейных? Следуя рассмотренному выше принципу, мы получили бы сеть на рис. 9.3.
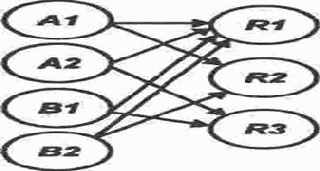
Легко видеть, что максимальное возбуждение, соответствующее решению /И, достигается всегда, когда задана ситуация, требующая максимального возбуждения только лишь нейронов R2 или R3. Сеть дает побочный эффект, что требует корректировки решения. Она заключается в том, что если максимально и одинаково возбудились два нейрона выходного слоя и один из них R1, то верное решение соответствует второму. Если максимально возбудился только нейрон R1, то он представляет правильное решение.
В данном случае происходит коллизия при замене операций конъюнкции л и дизъюнкции v одной операцией &. Ведь логический предикат возбуждения решения R1 имеет вид
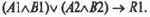
Благодаря этому справедлива гипотеза о минимальной длине статической цепочки в разд. 2.9.
Тогда легко провести коррекцию, построив обученную сеть так, как показано на рис. 9.4, введя так называемые скрытые нейроны 1 и 2.
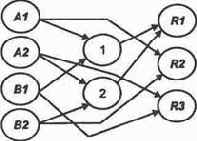
Рис.9.4. Обученная нейросеть
Выбор нейросети, обучение, трассировка. Мы построили нейросеть, пользуясь приемами, известными специалистам схемотехникам, разрабатывающим устройства компьютера. Мы соединили элементы связями — «проволочками», произведя трассировку для правильного распространения сигнала в соответствии с желаемой функцией. Как неоднократно указывалось выше, все это относится к уже обученной сети. Причем из рассмотрения полностью исключен тот параметр, настройка которого позволяет обучить сеть, в частности, проложить нужные "проводочки" и перекусить ненужные.
Нейрон в данном случае только выполняет передаточную функцию, один из видов которой и был рассмотрен. Более полная модель нейрона заключается в следующем. Нейрон имеет несколько входов — дендритов, каждый из которых обладает весом синапсической связи. В результате выполнения передаточной функции возбуждение нейрона через ветвящийся аксон передается дендритам других, связанных с ним нейронов. Дендрит воспринимает сигнал, пропорциональный своему весу. Таким образом и формируется сеть, в которой различаются входной и выходной слои. Передаточная же функция с учетом синапсических весов для нашего простейшего случая (при компьютерном моделировании чаще всего другого и не требуется) имеет вид
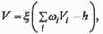
В результате весь смысл построения и обучения нейросети заключается в том, что синапсические веса регулируются, обусловливая пути прохождения возбуждений в сети.
В частности, представив некоторую абстрактную сеть и построив на ее основе сеть для игры в рулетку, положим некоторые веса связей, равными единице (наличие "проводочков"), а некоторые (или все оставшиеся) — равными нулю (отсутствие «проводочков»). Но ведь допустимы и некоторые промежуточные значения весов, хотя для практических целей наш подход оправдан.
Подойдем к построению нейросети для игры в железнодорожную рулетку иначе. Ранее сеть создавалась по известным условиям игры, теперь пусть нам задана нейросеть, а мы обучим ее для игры в рулетку.
Изобразим некоторый ориентированный ациклический граф (рис.9.5) и придадим ему смысл нейросети, поставив в соответствие его вершинам — нейронам (кроме предполагаемых рецепторов) все ту же передаточную функцию. Вот только как заставить сеть так реагировать на очевидные эталоны, чтобы максимального возбуждения достигали нейроны выходного слоя, соответствующие решениям? Для этого необходимо, полагая первоначально все веса нулевыми (или минимальными), увеличить некоторые из них до максимального значения или до единицы. Проще всего именно так и действовать: сначала все веса нулевые ("проводочки" есть, но их сопротивление чрезвычайно высоко), затем выбранные нами веса положим равными единице. Вышесказанное равносильно тому, что какието "проводочки" оставлены, а какието перекушены. Описанное действие по обучению нейросети мы называем трассировкой.
Продемонстрируем алгоритм трассировки, введя упрощения по сравнению с рассмотренным в разд. 3.
Компьютерная обработка нейросети значительно облегчается, если сеть представлена матрицей следования S (рис. 9.6, а), где наличие связи обозначается ее весом.
1. Произведем трассировку возбуждений нейронов [А\,
Исключим из матрицы S строки и столбцы, соответствующие не интересующим нас нейронам входного и выходного слоев. Матрица примет вид 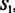
Присвоим нейронам, соответствующим нулевым строкам — входам матрицы 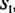
![]() = 2. Таким образом обеспечивается возможность повторного использования нейронов при получении других решений. Исключаем из матрицы
= 2. Таким образом обеспечивается возможность повторного использования нейронов при получении других решений. Исключаем из матрицы
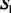
![]() принимает вид, приведенный на рис. 9.6, в.
принимает вид, приведенный на рис. 9.6, в.
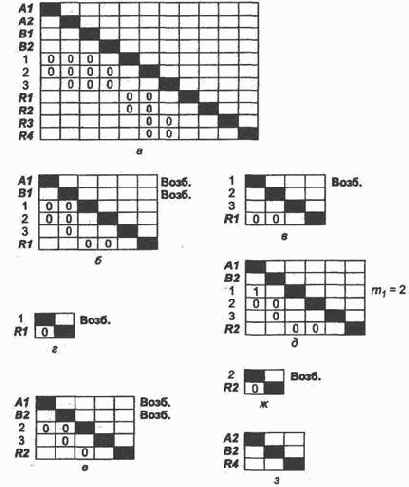
Рис. 9.6. Матрица следования для игры:
а — общий вид; б для трассировки первого решения;
в — первый шаг преобразования;
г — второй шаг преобразования;
д для трассировки второго решения;
е первый шаг преобразования матрицы следования для обучения второму эталону;
ж — второй шаг преобразования матрицы следования для обучения второму эталону;
