Проанализировав сказанное выше, попытаемся собрать некоторую универсальную модель нейросети с входным и выходным слоями. Картина возбуждений выходного слоя при подаче изображения на входной слой после аппроксимации в непрерывную область определения из дискретной будет представлять собой непрерывную функцию, максимум которой определяет необходимое заключение. Однако на этапе обучения, а также в рабочем режиме с удовлетворительной достаточно малой вероятностью по ряду предъявляемых эталонов этот максимум не совпадает с нужным ответом. Следовательно, путь распространения возбуждений внутри сети необходимо скорректировать изменением синапсических весов задействованных нейронов.
Как было упомянуто выше, предварительная локализация максимума величины сигнала производится в результате взаимодействия нейронов в области или некоторой окрестности выходного слоя или коры. Области возбуждений «закрепляются» за типами объектов — за буквами, цифрами, продуктами питания и т.д. В развитой сети с актуальным понятием коры нейроны отдельных ее областей через нейроны внутренних слоев вновь порождают пути прохождения возбуждений в другие области коры и т.д.
Пытаясь проанализировать и воспроизвести универсальную нейросеть, видим, что отдельный нейрон может взаимодействовать с огромным числом нейронов (нейрон имеет до 10 тыс. дендритов), но это взаимодействие носит локальный характер. А именно, несмотря на случайность связей, вероятность связи с «близким» нейроном значительно выше вероятности связи с нейроном «далеким». Об этом свидетельствуют исследования длины дендритов и аксонов: длина дендрита достигает миллиметра, а длина аксона — сотни миллиметров. При этом применяется, повидимому, усредненная характеристика, вряд ли отражающая нейроны только головного мозга.
Такой принцип локальности, пронизывающий всю структуру сети, в сочетании с принципом иерархии — возможностью построения новых выводов на основе сделанных, позволяет реализовать связи «каждый с каждым». Никакой вывод не остается недоступным и неиспользованным при построении сложных умозаключений.
Принцип локальности обеспечивает минимизацию входной информации, существенное влияние лишь значимых признаков на заключение, контролируемое и диагностируемое пофункциональное разбиение областей нейросети, определение и выделение той области нейросети, в синапсические веса которой необходимо внести поправки в процессе обучения.
Данный принцип не отвергает существования маловероятных связей «каждого с каждым». Эта вероятность может быть высокой вследствие аномалий генетического характера. Например, некий уникум способен «видеть» кожей: нейроны, воспринимающие кожные ощущения, сильно связаны с нейронами выходного слоя, «отвечающими» за зрение. При слабых связях распространение возбуждения от кожных рецепторов в сторону «зрительных» нейронов гаснет. В данном же случае оно становится результативным, поскольку в целом все нейроны устроены одинаково.
Большое число связей способствует высокой надежности мозга. Ведь ежедневная гибель огромного числа нейронов, подхлестнутая алкоголем и наркотиками, а также травмы компенсируются другими путями прохождения возбуждений, иногда даже связанными с Необходимостью переобучения. Впрочем, ограниченный ресурс возможного не спасает в конце концов от деградации.
Рассмотрим теперь более подробно процесс локализации максимальной величины возбуждения на выходном слое, заключающейся в выделении того нейрона некоторой малой области, величина возбуждения которого максимальна. Он основан на подавлении тех сигналов, которые не соответствуют нейрону с максимальным возбуждением т.е. концентрация сигнала и выделение нейрона с максимальной величиной возбуждения достигаются с помощью подавляющих связей «соседних» нейронов выходного слоя.
Пусть нейронам выходного слоя, условно расположенного на плоскости (х,у), соответствует непрерывная функция возбуждения Р(х,у) (рис. 1.7), обусловленная прохождением сигналов возбуждений в сети на основе предъявленного эталона. Будем считать, что эта функция имеет один или более максимум. Пусть
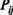
Каждый нейрон (i,j), действуя в своей окрестности, рассылает соседним нейронам, на их дендриты с отрицательными, не обязательно регулируемыми весами первоначальную величину возбуждения
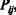
![]() с разными значениями величин возбуждения. Пусть
с разными значениями величин возбуждения. Пусть 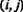
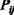
![]() Тогда в течение очередного периода тактовой частоты на входе нейрона
Тогда в течение очередного периода тактовой частоты на входе нейрона
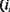
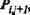
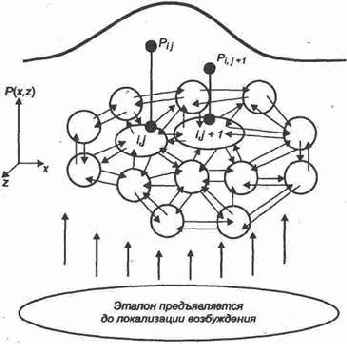
Рис.1.7. Локализация возбуждения нейронов выходного слоя
При предъявлении на входном слое эталона, т.е. при существовании в некоторый период времени характера и величины возбуждений, обусловливающих возбуждение выходного слоя, между нейронами (i,j) и (i,j+1) происходит перераспределение величины возбуждения. А именно значение
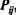
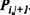
Рассматривая этот процесс в рамках взаимодействия всех нейронов области выходного слоя, можно сделать вывод о постепенной концентрации высокого уровня возбуждения, присущего одному или нескольким нейронам и определяющего один или несколько локальных максимумов.
При таком взаимодействии нейронов области возбуждения выходного слоя происходит усиление сигнала наиболее возбужденного нейрона. Полное подавление сигнала возможно только на границе этой области. Если гдето внутри области возбуждение некоторого нейрона окажется подавленным полностью (сигнал не преодолевает порога), то в следующем такте этот нейрон не сможет подавить сигнал того нейрона, который прежде имел более слабый сигнал возбуждения. Тогда возможно появление в указанной области возбуждения нового локального максимума. Таким образом, веса отрицательных связей должны способствовать максимизации возбуждения того нейрона, который первоначально продемонстрировал максимальное возбуждение при затухании возбуждения нейронов в сторону периферии.
Но всегда ли следует на выходном слое локализовать величину возбуждения?
Повидимому, такое усиление возбуждения используется для того, чтобы единственный нейрон выходного слоя преодолел некоторый порог, будучи ответственным за сделанный вывод или решение.
Локализация и максимизация возбуждения на выходном слое особенно важны тогда, когда действительно необходима высокая степень определенности, например в том случае, если получаемый вывод (решение) немедленно участвует в цепочке последующих выводов.
В конце концов все обусловлено назначением сети решаемой задачей. Можно представить себе аттракцион — реакцию фантастического чудовища на изображение, как это показано на рис.
По виду изображения инициируются те или иные программы — радости, гнева, поднятия лап, виляния хвостом и т.д. Возбуждение определенных нейронов выходного слоя связывается с запуском соответствующих программ, где основным параметром является величина возбуждения. Программы не исключают друг друга и могут запускаться в одном такте. При этом предпочтителен запуск только тех программ, значение параметра которых превышает некоторый порог.
В большинстве частных случаев, когда нейросеть обучается с помощью «учителя», т.е. на основе действий извне при ее настройке, присутствует элемент принудительного закрепления нейронов выходного слоя за выводами. В процессе последующего обучения преимущественно с помощью весов синапсических связей добиваются адекватной реакции сети.
Отметим в заключение, что научный аспект проблемы развития и внедрения нейросетевых технологий базируется на философско математическом представлении задач ИИ , выражающемся в формализации процесса мышления.
В работе Д. А. Поспелов, в частности, исследует теорию Аристотеля силлогистику и предлагает принципы ее моделирования. Тем самым указывается важность формализации механизма мышления. Этим механизмом уже давно, со времен Лейбница и до появления булевой алгебры (вплоть до наших дней), является математическая логика, отображенная во многих работах выдающихся математиков.
Математическая логика, ее важный раздел «Алгебра высказываний», действительно соединили принципы мышления и их автоматизированное воплощение.
Однако для реализации мышления природа не создала ничего лучшего, чем человеческий мозг. Он является гигантской нейросетью, фиксирующей причинноследственные связи, создающей базу знаний и владеющей процедурами логического вывода.
Таким образом, нейронные сети реально являются основой формализации средств мышления. Поэтому справедливо считать, что исследование нейронных сетей опирается на достижения математической логики.
