В работе рассматривается возможность моделирования электрически коротких длинных линий связи при помощи математического пакета Mathematica.
Пакет Mathematica был выбран потому, что он содержит мощное и универсальное ядро, способное работать на различных компьютерных платформах; ориентированное на математические расчеты и приложения; современный пользовательский интерфейс, обширные пакеты применения и расширения системы, представление графики , в том числе динамической, мультимедиа - воспроизведение динамических (анимационных) изображений и синтез звуков с поддержкой звуковой платы. Система обладает способностью адаптироваться - обучаться новым математическим законам и закономерностям, пополняться новыми функциями. Его применение весьма перспективно в инженерной практики.
Опишем математические модели короткой и длинной линий [1].
Короткая линия . Обобщённая модель линии связи состоит из совокупности сосредоточенных элементов цепи, как изображено на рис. 1.
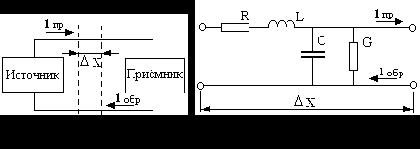
Два вентиля соединяются короткой линией связи, которая может быть представлена в виде двух моделей: ёмкостной и индуктивной. Независимо от характера модели, качественно форма сигнала имеет одинаковый вид для обоих вариантов. Качественно короткая линия проявляется в затягивании фронта информационного сигнала (рис. 2), что приводит к снижению системного быстродействия.
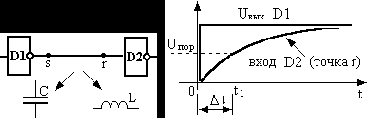
Рис. 2. Искажения сигнала в короткой линии
Проведём более детальную оценку снижения быстродействия. Начнём с линии, имеющей ёмкостной характер. Учтем, что: Rвых<<Rвх и постоянная времени линии tл=RC =RвыхCл. Теперь запишем конечную формулу изменения напряжения на входе микросхемы 2, которое фактически есть выражение заряда емкости линии связи Сл:
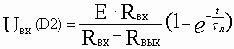
Учитывая, что Rвых << Rвх, получаем формулу для расчета входного напряжения через постоянную времени линии
где E, Rвых, Сл - известные параметры.
Рассмотрим теперь короткую линию индуктивного характера. Вместо параллельной ёмкости появилась последовательная индуктивность. Постоянная времени линии:
Помним, что Rвых << Rвх. Таким образом, нам известна постоянная времени tл. Эта постоянная времени используется при расчёте напряжения. В инженерной практике на предварительных этапах проектирования задаются значением порога срабатывания микросхемы: Uпор=0,5U1, при этом снижение системного быстродействия определяется как Dt=0,7tл. Для повышения быстродействия системы, следует всегда стремиться к уменьшению Dt.
Длинная линия. Режим переключения из 0 в 1. .
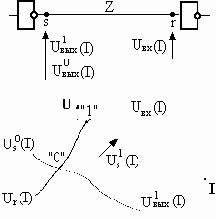
Рис. 3. Граничные условия задачи при расчете длинных линий
Пусть Z - волновое сопротивление линии, Т - время пробега (сигнала) от начала до конца линии. Решение задачи будем проводить методом характеристик [1]. Исходные данные:
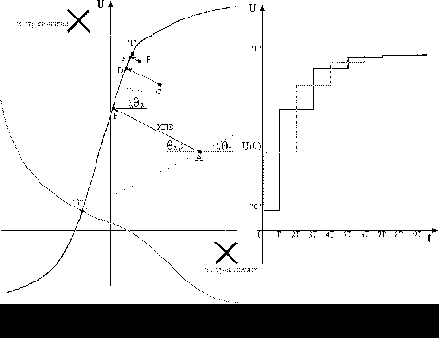
· Граничные условия задачи: вольтамперные характеристики U1вых(I), U0вых(I) и Uвх(I), и параметры генератора - Uг(t) (рис. 3).
· Начальные условия: напряжение на входе линии в начальный момент
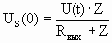
Алгоритм решения иллюстрируется графически (рис.4). Решим эту задачу пошаговым продвижением.
Шаг первый. Наносим граничные условия задачи. На рисунке они изображены для ТТЛ-схем. Если на концах линий стоят сопротивления, то граничные условия являются прямыми и их угол наклона берется равным:
qZ=arctgZЧM, где Z=(L/C)1/2- волновое сопротивление, M = mU/mI = масштаб по оси U/масштаб по оси I = A/B. (целесообразно выбирать масштаб, чтобы при Z=75 Ом угол равнялся 450).
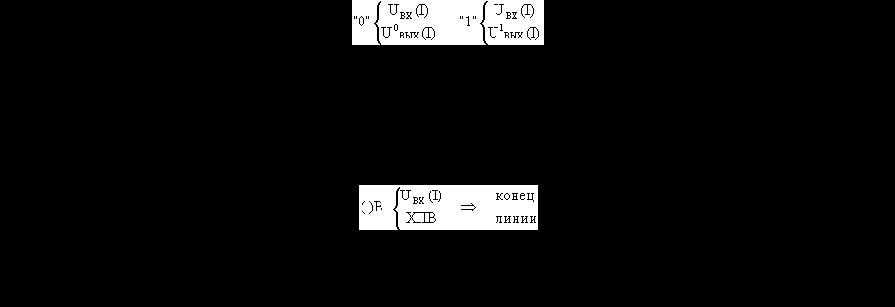
Расчёт формы сигнала при переключении МС из единицы в ноль (1 > 0) . Методика расчёта прежняя, как и при переключении из 0 в 1. Решение задачи ведётся обычным образом. В данном случае рассматриваем ТТЛ-схемы. Итак, на первом шаге строим нагрузочную прямую под углом qz из точки статического состояния лог. 1. Точка А соответствует входному напряжению на линии при t = 0. Таким образом, начальные условия (уровень сигнала, поступающий на линию) определяется точкой А. Далее строим ХПВ из точки А под углом -qz. Полученная точка B - конец линии. Следующий шаг - построение ХОВ из точки B под углом +qz. И так далее, далее… Сделаем некоторые замечания.
Замечание 1. При решении задачи необходимо оговаривать некоторое поле d в окрестностях статического режима, при попадании в которое задача считается решённой. Каково значение d? - Это зависит от конкретной задачи, которую предстоит решить. В зависимости от опасности нестыковки, назначения аппаратуры, и прочего, и прочего… d составляет около 3...5%.
Замечание 2. При наличии последовательности импульсов помехи отражения от одного перепада (фронта или спада) накладываются на помехи следующего перепада. При проектировании необходимо добиваться, чтобы помехи, вызванные одним импульсом (перепадом) не влияли бы на другой импульс. Важно добиваться прекращения помех отражения до наступления следующего импульса.
Содержание раздела
