Числа Фибоначчи - золотая пропорция
После первых нескольких чисел в последовательности, отношение любого числа к следующему старшему равна примерно 0.618 к 1, а к соседнему младшему – приблизительно 1.618 к 1. Чем дальше вдоль последовательности, тем ближе отношение приближается к фи, которое является иррациональным числом 0.618034… Соотношение между числами, расположенными через одно в последовательности, приблизительно равно 0.382, что является инверсией от 2.618 (1:2.618*). Обратитесь к таблице соотношений всех чисел Фибоначчи от 1 до 144 (рис.3-2).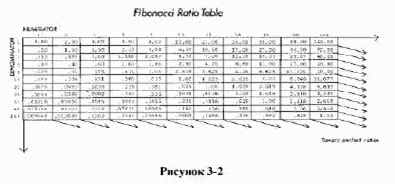
Фи является единственным числом, которое после сложения с 1 дает свою же инверсию:
0.618+1=1:0.618. Такой альянс аддитивных и мультипликативных свойств порождает следующую последовательность равенств:
0.6182 = 1 - 0.618,
0.6183 = 0.618 - 0.6182,
0.6184 = 0.6182 - 0.6183,
0.6185 = 0.6183 - 0.6184, и т.д.
или, альтернативно:
1.6182 = 1 + 1.618,
1.6183 = 1.618 + 1.6182,
1.6184 = 1.6182 + 1.6183,
1.6185 = 1.6183 + 1.6184, и т.д.
Некоторые формулировки из взаимосвязанных свойств этих четырех соотношений могут быть представлены следующим образом:
1) 1.618 - 0.618 = 1,
2) 1.618 * 0.618 = 1,
3) 1 - 0.618 = 0.382,
4) 0.618 * 0.618 = 0.382,
5) 2.618 - 1.618 = 1,
6) 2.618 * 0.382 = 1,
7) 2.618 * 0.618 = 1.618,
8) 1.618 * 1.618 = 2.618.
Кроме 1 и 2, любое число Фибоначчи, умноженное на 4 и добавленное к некоторому выбранному числу Фибоначчи, дает еще одно число Фибоначчи:
3 * 4 = 12; + 1 = 13,
5 * 4 = 20; + 1 = 21,
8 * 4 = 32; + 2 = 34,
13 * 4 = 52; + 3 = 55,
21 * 4 = 84; + 5 = 89, и т.д.
Так как развивается новая последовательность, третья последовательность начинается с тех же чисел, которые добавлялись к произведению на 4. Это соотношение возможно, потому что коэффициент между числами Фибоначчи, отстоящими друг от друга через две позиции равен 4.236, где 0.236 является и инверсией этого коэффициента, и разностью с числом 4. Это непрерывное рядообразующее свойство отражается и в других соотношениях по этим же причинам.
1.618 (или 0.618) известно как Золотая пропорция или Золотое сечение. Его гармония приятна для глаз и является важным явлением в музыке, искусстве, архитектуре и биологии. Вильям Хоффер, написал для декабрьского номера 1975 года журнала Smithsonian Magazine:
«…пропорция 0.618034 к 1 является математической основой для формы игральных карт и Пантеона, подсолнухов и раковин улиток, греческих ваз и спиральных галактик открытого космоса. Греки многое сделали в своем искусстве и архитектуре по этой пропорции. Они называли это «золотым сечением».
Абсурдные кролики Фибоначчи всплывают в самых неожиданных местах. Эти числа, бесспорно, являются частью мистической естественной гармонии, которая приятно осязается, приятно выглядит и даже приятно звучит. Музыка, например, основана на 8-ми нотной октаве. На фортепьяно это представлено 8 белыми клавишами и 5 черными – всего 13. Не случайно, что музыкальная гармония, которая, как кажется, приносит уху величайшее удовольствие, является мажорным шестизвучием. Нота Е (ми*) звучит как соотношение 0.625 к ноте С (до*). Всего лишь на 0.006966 больше точного Золотого сечения, соотношения мажорного шестизвучия вызывают приятные колебания в улитке внутреннего уха – органа, который как раз имеет форму логарифмической спирали.
Непрерывное нахождение чисел Фибоначчи и золотой спирали в природе точно объясняет, почему пропорция 0.618034 к 1 так привлекательна в искусстве. Человек видит изображение жизни в искусстве, которое основано на золотом сечении.
Природа использует Золотое сечение в своих наиболее сокровенных строительных блоках и в наиболее продвинутых образцах, от таких мелких форм, как атомные структуры, микрокапилляры мозга и молекулы ДНК до таких огромных, как планетарные орбиты и галактики. Оно касается таких разнообразных явлений, как расположение квазикристаллов, планетарных расстояний и периодов обращения, отражения световых лучей от стекла, мозг и нервная система, музыкальная аранжировка и строение растений и животных. Наука быстро доказывает, в природе действительно существует основной закон пропорций. Между прочим, вы удерживаете предмет двумя из пяти ваших отростков (две руки, две ноги и голова*), которые имеют три шарнирно соединенных части (плечо, предплечье и кисть*), пять отростков на концах (пальцы*) с тремя шарнирно соединенными частями (фаланги пальцев*). (Авторы намекают на волновую последовательность 5-3-5-3.*)
