Е. Расширения в 5-волновой фигуре

При анализе расширений в 5-волновой фигуре требуется допол­нительный параметр, основанный на ряде суммирования Фибо­наччи, подтверждающий расчет ценовой цели для расширений 3-волновой фигуры, основанных на ФИ Фибоначчи.
Чтобы проанализировать 3-волновую фигуру, мы умножали ве­личину первой импульсной волны на отношение Фибоначчи 1,618. Полученное произведение прибавляли к размеру колебания первоначального движения. Таким образом, вычислялась линия ценовой цели Фибоначчи. Именно на этой линии мы ожидали разворота третьей волны.
Поскольку обычно мы имеем на трендовом рынке более трех волн, наш подход к вычислению ценовой цели Фибоначчи следует слегка модифицировать. Наиболее распространенная ценовая фигура имеет, по крайней мере, пять волн, три из которых им­пульсные волны, а две — корректирующие (рисунок 3.24).



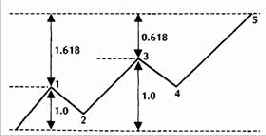
Рисунок 3.24 Расчет ценовой цели Фибоначчи в правильном 5-волновом движении.

В правильном 5-волновом движении восходящего тренда ли­ния ценовой цели конца волны 5 рассчитывается умножением амплитуды волны 1 на отношение Фибоначчи ФИ = 1,618 и затем умножением амплитуды от основания волны до вершины волны 3 на обратное значение отношения Фибоначчи ФИ (ФИ' = 0,618). В нисходящем тренде также умножаем первоначальный размер колебания на 1,618 и умножаем амплитуду от максимума волны 1 до минимума волны 3 на отношение 0,618.
Объединив два эти расчета — использующие отношения 0,618 и 1,618 — можно заранее точно вычислить цену окончания волны 5 при условии, что рынок движется в рамках правильной ценовой фигуры, описанной выше.
На практике, однако, в большинстве случаев дело обстоит не так. Вместо того, чтобы в результате расчета с применением обоих отношений получить один и тот же уровень цен, мы имеем две различные цены. Они могут быть удалены друг от друга на боль­шее или меньшее расстояние, в зависимости от амплитуды волны 1 и волны 3. Мы видим верхнюю и нижнюю ценовые цели, опре­деляемые как полоса ценовых целей Фибоначчи.
Можно ли знать, будет ли когда-либо достигнут наш ценовой прогноз? Абсолютно нет. Но мы знаем заранее, будет ли узкой или широкой ценовая полоса, рассчитанная умножением 1,618 на раз­мер волны 1 и 0,618 на расстояние от вершины или основания волны 1 до основания или вершины волны 3.
Если верхний и нижний уровни полосы целевых цен Фибонач­чи близки друг к другу относительно величины базового колеба­ния первоначального движения первой импульсной волны, поло­су ценовых целей стоит принять во внимание.


Ценовые цели, построенные из расширений в правильных 3-волновых фигурах, обычно связаны с "мягкими" биржевыми товарами типа сои, апельсинового сока или свиной грудинки. Они (цены) могут совершать значительные движения, вызывае­мые докладами о состоянии урожая, складских запасов, а также прогнозами погоды. Расширения на рынках этих продуктов мо­гут достигаться в пределах пары дней. Однако работа с расшире­ниями на рынках этих продуктов опаснее, потому что ценовые цели имеют тенденцию не достигаться с небольшим разрывом, превышаться с небольшим отрывом или даже превышаться со значительным отрывом.
Ценовые цели Фибоначчи в расширениях наличных валют, финансовых продуктов, фьючерсов, фьючерсов фондовых Инде­ксов или акций в 3-волновых движениях достигаются очень ред­ко. Обычно требуется пять или более волн, прежде чем будет достигнута ценовая цель. Поэтому могут пройти недели и месяцы, прежде чем мы доберемся до нашей ценовой цели. Точное время в значительной степени зависит от амплитуды первоначальной им­пульсной волны.
Когда в этой главе мы анализировали коррекции, то не реко­мендовали анализировать графики на недельной основе. Напро­тив, используя расширения как инструменты Фибоначчи, мы вы­бираем комбинацию дневного и недельного анализа. По сравне­нию с дневным подходом недельный анализ расширений дает бо­лее определенную картину потенциальных точек разворота на рынках, даже несмотря на то, что 5-волновой отсчет может ока­заться не столь четким, как на дневных графиках.
Поскольку расширениям нужно больше времени для развития и они инструменты, более ориентированные на среднесрочный анализ, нас будут главным образом интересовать важные измене­ния тренда и важные движения на рынках. Мы часто видим пять главных волн на недельной основе, когда достигается ценовая цель. Важные колебания на недельной основе, конечно, состоят из многих меньших дневных волн, которые могут показывать формирование расширений. Эти волны, однако, не используют­ся, потому что размер их колебания для проведения прибыльных сделок слишком мал.
Анализ Эллиота отдал приоритет 5-волновому отсчету на днев­ной основе. При идентификации 5-волновых фигур для расчета расширений мы сначала изучаем дневной график. Если не нахо­дим конфигураций пик/впадина в колебании соответствующего размера, проверяем недельные данные и выполняем отсчет волн оттуда.
Анализ расширений 3-волновых фигур заставил нас сомне­ваться в возможности многократного подтверждения ценовых целей дополнительными отношениями Фибоначчи. Если те­перь интегрирование 5-волновых движений позволит нам вы­числять коридоры целевых цен Фибоначчи, инвесторы получат очень хорошее указание, какую ценовую цель использовать. Пока верхняя и нижняя границы ценовой полосы находятся близко друг к другу, можно использовать их как достоверные це­новые индикаторы.
Решение о том, находятся ли ценовые полосы достаточно близко друг к другу, зависит от типа базового продукта торговли. Индекс DAX30 представлен в качестве первого примера успешно­го применения расширения в 5-волновых фигурах. Для Индекса DAX30 мы считаем полосу целевых цен Фибоначчи достаточно узкой, пока расстояние от ее нижней до верхней границы состав­ляет менее 200 пунктов (например, от 6,500.0 до 6,700.0).
Индекс DAX30 проанализирован за период с января 2000 года по декабрь 2000 года с сочетанием дневного и недельного подхо­дов. Коридор целевых цен Фибоначчи рассчитан на недельной ос­нове. Затем проанализирован дневной график, чтобы определить пункты входа и выхода для сигналов, возникавших, когда движе­ния цены Индекса DAX30 достигали коридора цен.
Если мы установим коридор целевых цен Фибоначчи на 200 пунктов, то сможем рассчитать ценовую полосу Индекса DAX30 для соответствующего периода (рисунок 3.25).





Величина колебания импульсного движения от максимума на рисунке 3.25 на уровне 8,136.0 до минимума на 7,412.0, умножен­ная на 1,618, дает нам верхнюю границу коридора ценовых целей 6,305.0. Нижняя граница ценовой полосы рассчитывается умно­жением на 0,618 расстояния от максимума волны 1 на 8,136.0 до минимума волны 3 (на рисунке 3.25 от пика №3 до впадины №4) на 6,937.0, что дает 6,197.0. Расстояние от 6,305.0 до 6,197.0 мень­ше, чем 200 пунктов, принятые в качестве максимально допусти­мого размера коридора ценовых целей Фибоначчи.



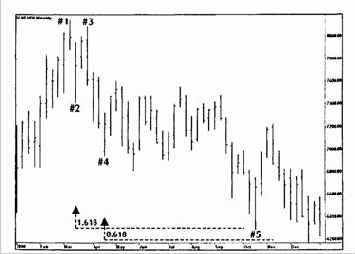
Рисунок 3.25 График Индекса DAX30 с января по декабрь 2000 года. Ко­ридор ценовых целей рассчитан с использованием ФИ Фи­боначчи = 1,618 и ФИ' = 0,618.

Работа с ценовыми полосами важна, потому что мы не приме­няем дополнительные правила входа к нашей стратегии, как дела­ли это при анализе коррекций и расширений 3-волновых фигур. Вместо этого, когда достигается ценовая полоса, мы сразу же вхо­дим на рынок по цене закрытия дня.

Дополнительные параметры для генерации сигналов для Индекса DAX30 при использовании расширений в сочетании с ценовыми полосами на основе 5-вол-нового движения:
• минимальный размер колебания 300 пунктов (например, движение от 6,500.0 до 6,800.0); целевая прибыль в 50% пол­ного расстояния от максимума волны 1 до минимума волны 5 для сигнала покупки (для сигнала продажи — наоборот);
• плавающий стоп на четырехдневном максимуме или мини­муме; уровень стоп-лосса на пике или впадине перед входом; правило повторного входа после срабатывания стоп-лосса на закрытии, которое выше или ниже цены закрытия при пер­воначальном входе.

Как объяснялось ранее, ценовые цели, рассчитанные на не­дельных данных, интегрируются и превращаются в сигналы на дневных графиках. Рисунок 3.26 иллюстрирует сигнал покупки для Индекса DAX30 при выходе из коридора ценовых целей Фи­боначчи.
При подсчете прибылей/убытков оказывается, что длинная позиция в Индексе DAX30, открытая на 6,534.5, дает прибыль в почти 700 пунктов. Что касается правила выхода, мы рассматрива­ем только уровень целевой прибыли, вызывающий продажу пози­ции на уровне 7,222.0, как раз перед разворотом рынка в нижнюю сторону. При использовании плавающего стопа позиция была бы продана четырьмя днями позже со слегка меньшей прибылью.


Чтобы доказать, что прибыльная длинная сделка на Индексе DAX30 не исключительный случай и можно применять 5-волно-вой отсчет для вычисления расширений на дневных данных (если можно использовать достаточно большое первоначальное колеба­ние), мы рассчитаем подобный коридор ценовых целей, основан­ных на отношениях Фибоначчи 1,618 и 0,618, для дневной налич­ной японской иены.



Рисунок 3.26 График Индекса DAX30 с января по декабрь 2000 года. Мо­делирование торговых сигналов на основе расширений и це­новых целей Фибоначчи.

Начав с максимума волны 1 (110,03) и соответствующего ми­нимума (107,72), умноженных на 1,618, получаем ценовую цель 103,99. Подтверждение от максимума волны 1 до минимума волны 3, умноженное на 0,618, приводит нас ко второй ценовой цели 104,08 (рисунок 3.27).
Получившаяся полоса цен Фибоначчи чрезвычайно узка и идеальный пример того, что мы ищем на рынках. Наличная япон­ская иена упала до 103,94 и затем немедленно развернула направ­ление своего тренда вверх.



После создания полос ценовых целей Фибоначчи из 5-волно-вых движений, многократное подтверждение ценовых целей на расширениях откроет горизонты для прогнозирования важных изменений цены на рынке. Ценовые полосы — наиболее важный параметр анализа расширений 5-волновых движений. Мы нико­гда не сможем знать наверняка, дойдет ли цена рынка до ценовых целей, но, если она вошла в коридоры, они могут быть очень мощ­ными и надежными торговыми инструментами Фибоначчи.



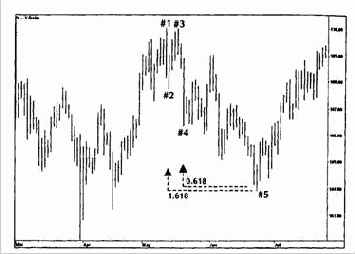
Рисунок 3.27 График наличной японской иены с марта по июль 2000 года. Коридор ценовых целей рассчитан с использованием ФИ Фибоначчи = 1,618 и ФИ' = 0,618.

Мы определили отношение Фибоначчи ФИ и его производные как воплощения закона природы и человеческого поведения. За­крывая эту главу, мы свяжем наши результаты по расширениям 5-волновых фигур с рядом суммирования Фибоначчи и проанали­зируем оба инструмента, используя интегрированный подход.


Содержание раздела

---