Нормальное и логнормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
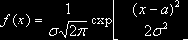
Нормальное распределение определяется двумя параметрами: математическим ожиданием


и на графике представляет собой симметричную колоколообразную кривую Гаусса, имеющую максимум в точке, соответствующей значению
и


от центра распределения. Изменение параметра


кривая вытягивается в центре и быстрее приближается к оси абсцисс при удалении от центра.
Часто вместо случайной величины Х целесообразно рассматривать нормированную случайную величину
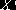
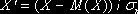
. Нормированная величина имеет математическое ожидание, равное нулю и дисперсию, равную единице. При а=0 и
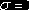
Ее уравнение:
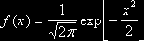
Между абсциссами
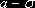

расположено 68,27% всей площади кривой нормального распределения. Это означает, что 68,27% всех измеренных единиц отклоняется от среднего значения не более чем на


. Площадь, заключенная между ординатами, проведенными на расстоянии
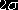
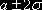
. И наконец, 0,9973 или 99,73% всех единиц находятся в пределах
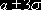
находится не более 0,27% всех значений величин, иными словами, 27 реализаций на 10 тыс. испытаний. Исходя из принципа невозможности маловероятных событий такие события можно считать практически невозможными. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
В технических приложениях принято при оценке результатов измерений работать с долями площади кривой нормального распределения, равными 95, 99 и 99,9%. Этим значениям соответствуют ординаты, равные следующим долям среднего квадратического отклонения: +/-1,96; 2,576 и 3, 291.
Условия широкого применения нормального распределения связаны с центральной предельной теоремой Чебышева, которая утверждает, что распределение какого-либо признака (параметра) при действии на него большого числа независимых причин сводится к нормальному независимо от вида исходного распределения. Согласно неравенству Чебышева при любом типе распределения не менее 88% его значений будут в диапазоне +\- 3SD.
Логнормальное распределение - это распределение, в которой нормальное распределение имеет логарифм случайной величины:
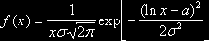
Изменение цены актива в будущем - случайный процесс, который в принципе должен описываться нормальным распределением. В то же время для целей вероятностной оценки стоимости актива в теории пользуются не нормальным, а логнормальным распределением. Это обусловлено следующими причинами. Во-первых, нормальное распределение симметрично относительно ее центральной оси и может иметь как положительные, так и отрицательные значения; однако цена актива не может быть отрицательной. Во-вторых, нормальное распределение говорит о равной вероятности для значений переменной отклониться вверх или вниз. В то же время на практике, например, имеет место инфляция, которая оказывает давление на цены в сторону их повышения, а также сама временная сущность денег: стоимость денег сегодня меньше, чем стоимость денег вчера, но больше, чем стоимость денег завтра. Кривая логнормального распределения всегда положительна и имеет правостороннюю скошенность (асимметрично), т.е. она указывает на большую вероятность цены отклониться вверх. Поэтому если, допустим, цена актива составляет 50 долл., то кривая логнормального распределения свидетельствует о том, что опцион пут с ценой исполнения 45 долл. должен стоить меньше опциона колл с ценой исполнения 55 долл., в то время как в соответствии с нормальным распределением они должны были бы иметь одинаковую цену. Хотя нельзя надеяться, что приведенные исходные предположения в точности выполняются во всех реальных рыночных ситуациях, тем не менее принято считать, что логнормальное распределение достаточно хорошо как первое приближение в случае активов, которыми торгуют на конкурентных рынках аукционного типа для длинных рассматриваемых периодов.
Содержание раздела
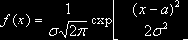

 и на графике представляет собой симметричную колоколообразную кривую Гаусса, имеющую максимум в точке, соответствующей значению
и на графике представляет собой симметричную колоколообразную кривую Гаусса, имеющую максимум в точке, соответствующей значению 
 и
и 
 от центра распределения. Изменение параметра
от центра распределения. Изменение параметра
 кривая вытягивается в центре и быстрее приближается к оси абсцисс при удалении от центра.
кривая вытягивается в центре и быстрее приближается к оси абсцисс при удалении от центра.
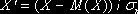 . Нормированная величина имеет математическое ожидание, равное нулю и дисперсию, равную единице. При а=0 и
. Нормированная величина имеет математическое ожидание, равное нулю и дисперсию, равную единице. При а=0 и
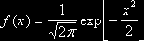
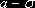
 расположено 68,27% всей площади кривой нормального распределения. Это означает, что 68,27% всех измеренных единиц отклоняется от среднего значения не более чем на
расположено 68,27% всей площади кривой нормального распределения. Это означает, что 68,27% всех измеренных единиц отклоняется от среднего значения не более чем на
 . Площадь, заключенная между ординатами, проведенными на расстоянии
. Площадь, заключенная между ординатами, проведенными на расстоянии 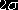
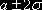 . И наконец, 0,9973 или 99,73% всех единиц находятся в пределах
. И наконец, 0,9973 или 99,73% всех единиц находятся в пределах 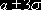
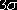 находится не более 0,27% всех значений величин, иными словами, 27 реализаций на 10 тыс. испытаний. Исходя из принципа невозможности маловероятных событий такие события можно считать практически невозможными. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
находится не более 0,27% всех значений величин, иными словами, 27 реализаций на 10 тыс. испытаний. Исходя из принципа невозможности маловероятных событий такие события можно считать практически невозможными. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.