Расчет годовых ставок процента
Очевидно, что при одинаковых условиях (одинаковый срок, простой или сложный процент) выгоднее та инвестиция, у которой выше процентная ставка. Однако зачастую сроки инвестиций и периоды выплат по ним не совпадают. В этом случае для того, чтобы сравнивать инвестиции, необходимо рассчитывать их процентные ставки, приведенные к одному и тому же временному периоду. Как правило, в качестве такого периода выбирается год.Пример 3 Сравнить, какой из банковских вкладов выгоднее:
а) вложение 1000 рублей в банк на месяц под 3% в месяц;
б) вложение 500 рублей в банк на 6 месяцев под 12% за полгода.
Можно вычислить, каков доход в процентном выражении за месяц во втором случае, и сравнить с уже данным показателем в первом случае. Однако традиционно в качестве такого периода берется один год.
При этом говорят, что ставка составляет Х процентов годовых.
Вычисление ставки в годовом исчислении можно производить по формуле простого или сложного процента.
Пример 4
По банковскому вкладу ежеквартально начисляют 2% от первоначальной суммы вклада. Найти годовую ставку процента.
Процентную ставку в периоде начисления умножают на число периодов в году:
Годовая ставка процента =ГхП=2% х4 квартала = 8% годовых
Пример 5 Вклад в банке дает 1°о за 14 дней. Найти годовую ставку процента.
Годовая ставка процента
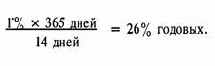
В общем случае она вычисляется из формулы (4) простого процента:
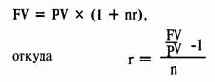
Если мы используем формулу сложного процента, то на единицу вложений годовая процентная ставка составит (1 + процентная ставка в периоде начисления в долях единицы), возведенная в степень, равную числу периодов начисления, минус единица:
(1 + r) n - 1.
Пример 6
По банковскому вкладу ежеквартально начисляют доход 2°о от первоначальной суммы вклада. Найти ставку процента (в годовых) с учетом реинвестирования полученного дохода.
(1 + 0,02)^ - I = 1,082432 - I = 0,0824.
Сравнивая результат примеров 1 и 3, можно сделать вывод,. что при прочих равных условиях инвестирования годовая процентная ставка с учетом реинвестирования выше.
В общем случае вычисляется из формулы (3):
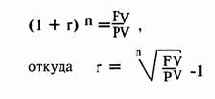
С учетом необходимости приведения процентных ставок к одному временному периоду их общие формулы расчета видоизменяются в зависимости от того, в каких единицах (днях, месяцах, кварталах) выражен период инвестирования.
Например, если инвестиция имеет срок, выраженный в днях, то число периодов п =-365/х, где х — число дней, то по формуле (6) процентная ставка равна:
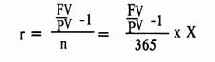
По формуле (7) процентная ставка равна:

Будучи рассчитана на основе одного временного периода (т. е. п = 1), формула приобретает совсем простой вид:
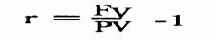
Содержание раздела