Достойно ли смиряться под ударами судьбы, иль надо оказать сопротивленье? he секрет, что настоящий профессионализм спекулянта проверяется не на восходящем тренде, а наоборот. Управлять рисками - почти то же самое, что управлять судьбой.
Поэтому риск-менеджмент, несмотря на свою молодость, очень быстро стал базовой парадигмой современных финансов.
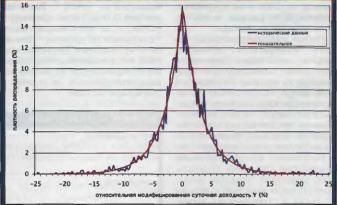
РИСУНОК 1 ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ АКЦИЙ РАО ЕЭС НА ММВБ С 22 08.97 ПО 31 08.2004 И ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Большую роль в развитии риск-менеджмента сыграли Базельский комитет по надзору за банками и финансовая компания J.P. Morgan.
В 1994 г. она первой раскрыла свою систему управления рисками - RiskMetrics, справедливо получившую широкое признание и распространение.
Во многом благодаря усилиям этих учреждений, основной мерой рыночного риска сейчас стал показатель VAR (Value At Risk) - предельная величина убытков по заданному портфелю активов, превышение которой на выбранном горизонте времени не может произойти с определенной вероятностью. Эту вероятность также называют доверительным уровнем и выбирают обычно в диапазоне 95-99%.
Впервые использование технологии VAR было рекомендовано The Global Derivatives Study Group (G30) в 1993 г. в исследовании Derivatives: Practice and Principles. Затем Европейский Совет в директиве ЕЕС 6-93 предписал определять резервирование капитала для покрытия рыночных рисков с использованием технологии VAR. В 1994 г. The Bank of International Settlements рекомендовал банкам раскрывать VAR по своим позициям.
В 1995 г. Базельский комитет одобрил технологию и предложил банкам использовать ее для расчета резервов капитала, а в 1996 году его поддержал Федеральный резервный банк США.
Прозрачность и относительная простота вычисления VAR, в свою очередь, во многом обусловлена возможностью использования семейства так называемых параметрических методов: дельта-нормалыюш метода, разработанного и реализованного в RiskMetrics, и многочисленных последующих модификаций. В основе этих методов лежит предположение о том, чтодоходность свободно торгуемого актива имеет логнормальное распределение вероятностей.
Но это не совсем так. В частности, всем известен эффект тяжелых хвостов реальных плотностей распределения.
Тем не менее, считается, что базисную гипотезу о логнормальности функции распределения всегда можно технично подправить с достаточной степенью точности.
Однако иногда это принципиально не так - функция распределения является совершенно другой.
В статье приводятся конкретные примеры того, что функция распределения доходности рыночного актива с очень высокой степенью достоверности подчиняется показательному закону распределения.
Итак, немного математики - без нее обойтись невозможно. По определению:
VAR = F^(l4x) (I)
где F^T(AV) - функция распределения вероятностей доходности Д? портфеля А на горизонте времени Т: AV=V(t+T)-V(t), где V(t) - стоимость портфеля в произвольный момент времени t, a F1 - обратная к ней функция, а - доверительный интервал. В дельта-нормальном методе делается предположение о нормальном (гауссовском) распределении случайной величины X log(V(t+T)/V(t)), которую можно
интерпретировать как доходность при непрерывном начислении процентов.
В этом случае реальная доходность портфеля Д? на интервале времени от t до t+T с высокой точностью равна XV(t) (при условии, что Д?/? много меньше 1). В случае, если математическим ожиданием X можно пренебречь, VAR(T) = -V(t)klnoT, где klo - (I-)% квантиль стандартного нормального распределения, от - среднеквадратичное отклонение нормального распределения Х(Т).
В данной работе в качестве альтернативы дельтанормальному методу предлагается использовать параметризацию функции распределения следующей случайной величины Y(T) (назовем ее модифицированной относительной доходностью):
r_ V(t + T)-V(t) min(F(/ + T),V(i))
Функция min (минимум) используется для того, чтобы сделать распределение Y симметричным и несмещенным при симметричном и несмещенном распре делении Д?.
Например, рассмотрим неслучайный процесс, в котором актив поочередно имеет стоимость V, и ?2. Математическое ожидание прибыли/убытка такого процесса М(Д?) равно О. Однако М(Д?/?) = -1/2(?-?2)г/?,?2 - всегда меньше нуля, т.е. смещено в отрицательную сторону.
Нетрудно убедиться, что величина Y(I) лишена этого недостатка.
Как будет показано ниже, в некоторых случаях величина Y распределена по показательному закону со
следующими плотностью распределения f(y) и функцией распределения вероятностей
F(y):/(')(3)
-е *\у О 21-е~^\у О 2(4)
где X - параметр распределения. В этом случае математическое ожидание M(Y) = 0, а среднеквадратичное отклонение o(Y) - к1.
Несомненным преимуществом распределения (3) и (4) является то, что оно определяется одним параметром к Это значительно упрощает его оценку по имеющимся историческим данным. Кроме того, данное распределение очень удобно для вычисления VAR, т.к. позволяет получить для него прямую аналитическую формулу.
Для этого необходимо заметить, что величина относительной прибыли/убытка Д?/?(0 (обозначим ее через х - именно эта величина интересует инвестора) в случае убытков следующим образом зависит от Y: х = Y/(I-Y), и наоборот Y=VO+x), тогда из формул (I) и (4) легко получаем:
VAR = V(t)
Л 1 іп(2 - 2 а) 1-Я1 Іп(2-2 а)= У(0сг1п(2-2ог) 1-о-1п(2 2а)(5)
Отметим, что поскольку для отрицательной убыточной половины распределения (3)-(4) всегда находится в интервале [1/2; 1], то VAR в (5) всегда находится в интервале [-V(t);0].
В качестве иллюстрации всего вышеперечисленного была построена функция плотности распределения суточной модифицированной относительной доходности Y (Т = 1 сутки) для обыкновенных акций РАО ЕЭС России по ценам открытия и закрытия на ММВБ с 22.08.1997 по 31.08.2004 (рис. 1).
Величина Y вычислялась по формуле (2) отдельно для цен открытия и цен закрытия каждого тортового дня (t) и следующего торгового дня (t+І) из указанного выше диапазона. На этом же рисунке дана кривая показательного распределения с параметром Х=0.32.
Нетрудно заметить, что совпадение графиков совершенно явно имеет не случайный характер.
Но несмотря на столь очевидное совпадение факта и теории, делать абсолютные выводы по одному примеру нельзя. Несомненно одно - применять в этом конкретном случае дельта-нормальный метод совершенно некорректно.
Не вызывает сомнения также и то, что необходимо и дальше проводить подобные исследования на других активах и временных горизонтах для того, чтобы открывать все новые горизонты финансовой науки и риск- менеджмента.