Копыркин К. - Динамические скользящие средние
В предыдущей статье на тему динамических скользящих средних мы рассмотрели предложенную Тушаром Шонде (Tushar Chande) Variable Index Dynamic Average, VIDYA. Напомню, что для вычисления VIDYA используется осциллятор Chande Momentum Oscillator (CMO), который представляет собой отношение между суммой положительных приращений цен и суммой отрицательных приращений цен за определенный период.
Однако это не единственный эффективный метод управления периодом усреднения скользящей средней в зависимости от текущего состояния рынка.
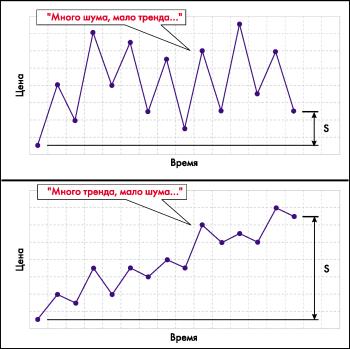
Рис. 1. Условное сравнение различных рыночных состояний.
Адаптивная скользящая средняя Перри Кауфмана
Перри Кауфман (Perry Kaufman) широко известен в кругах рыночных аналитиков и обозревателей с 70-х годов прошлого века. Он является автором шести книг, посвященных трейдингу, и редактором ежеквартального бюллетеня Kaufman on Market Analysis.
В 1995 году Кауфман представил в своей книге Smarter Trading оригинальный трендовый метод торговли, основанный на адаптивной скользящей средней (Adaptive Moving Average, АМА). Автор книги утверждает, что наиболее надежным видом торговли на рынках является консервативное следование направлению тренда.
Согласитесь, трудно спорить с данным замечанием.
Длинные тренды более предпочтительны для уверенной торговли, однако отслеживающие их индикаторы очень медленно отзываются на изменение рыночной динамики. К примеру, взгляните, как длиннопериодная скользящая средняя слабо реагирует на резкие, но краткосрочные движения цен. Кроме того, торговый сигнал, поступающий от такой средней, зачастую появляется в то время, когда цены уже закончили свое движение в нужном направлении.
Вот тут-то и приходит на помощь предложенная Кауфманом адаптивная методика следования тренду. Ее суть заключается в быстром получении входных сигналов на динамичном движении цен и своевременном закрытии позиций, когда рынок становится ненаправленным.
Однако Кауфман предостерегает, что при таком подходе необходимо умело отделять от основной тенденции присутствующие в ней случайные шумовые компоненты.
Коэффициент эффективности рынка
Любые ценовые движения можно условно разделить на две составляющие общее движение цены за выбранный период времени и шум в виде колебаний цены внутри этого периода. При этом разные рынки в различные периоды времени могут демонстрировать широкий спектр взаимных отношений шумового и трендового компонентов (рис. 1). Чем выше уровень шума в движении цен, тем труднее выделить направление и силу основной тенденции.
Следовательно, в этом случае необходимо применять более медленные методы идентификации тренда. С другой стороны, на рынках с малым уровнем шума основная тенденция определяется достаточно легко и разумны более быстрые методы определения трендов, обеспечи-
Принцип вычисления коэффициента эффективности ER заключается в том, что Общее изменение цены делится на сумму случайных шумовых колебаний цены (1+2+3+...+10).
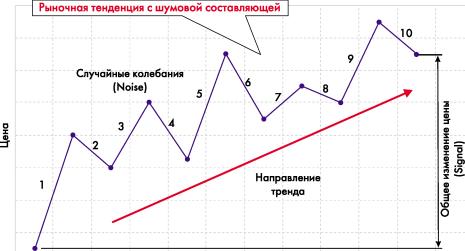
Для определения состояния рынка Кауфман применяет так называемый коэффициент эффективности (Efficiency Ratio, ER), который основан на сравнении общего движения цены и суммы шумовых движений рынка за определенный период. В оригинальных расчетах Кауфман использует 10дневный период, объясняя свой подход просто: десятка в вычислениях не меняет цифровых значений, а только перемещает десятичную точку.
К тому же 10 дней это две торговые недели или примерно половина торгового месяца.
Формула для вычисления коэффициента ER может быть представлена следующим образом: ER = Signal/Noise,
где
Signal = Abs(Price - Price(-n))
абсолютное значение разности между текущей ценой и ценой в начале периода вычислений; представляет собой общее движение цены за период;
Noise = Sum(Abs(Price - Price (-1)),n) сумма абсолютных значений ежедневных приращений цены в течение периода вычислений; является шумовой составляющей. Коэффициент эффективности (ER) может изменяться от 0 до 1. Значение ER будет равно нулю, когда на рынке нет направленного движения, а только шум. Значение ER будет равно единице, когда рынок движется однонаправленно, с полным отсутствием шума. На очень эффективном рынке общее движение цены будет равно изменению цены между точками начала и конца периода.
Представим себе ситуацию, когда цена двинулась вверх на 10 пунктов за 10-дневный период и при этом возрастала на один пункт каждый день. Мы можем посчитать коэффициент ER как 10/(10*1) = 1. В свою очередь, на очень неэффективном рынке, где произошло небольшое общее движение цены, но было много шумовых колебаний, значение ER стремится к нулю. Например, если цены сдвинулись только на 1 пункт за 10 дней, но движения цен каждый день составляли 10 пунктов то вверх, то вниз, коэффициент ER будет равен 1/(10*10) = 0,01. И конечно, если общее движение цены за выбранный период отсутствовало, а был только шум, значение ER будет равно нулю (рис.
2).
Еще немного формул
Следующий шаг в вычислении адаптивной скользящей средней применение коэффициента эффективности ER для управления периодом усреднения экспоненциальной скользящей средней (ЕМА). В соответствии с изложенным выше алгоритмом, мы должны применять быструю ЕМА с небольшим периодом усреднения на эффективном рынке с малым количеством шума и сильной трендовой составляющей.
С другой стороны, на рынке со слабым или отсутствующим трендом и высоким уровнем шума нам необходимо использовать медленную ЕМА с большим периодом усреднения. Кауфман предлагает применять 2-дневную ЕМА в качестве быстрой средней и 30дневную ЕМА в качестве медленной средней.
Коэффициент эффективности ER будет устанавливать скорость адаптивной скользящей средней между этими крайними значениями в каждый текущий момент в зависимости от состояния рынка.
Вспомним стандартную формулу экспоненциальной скользящей средней (ЕМА):
EMA = Price*SC + EMA_j*(1 SC),
где
SC = 2/(n+1) сглаживающая константа ЕМА (smoothing constant);
n период усреднения ЕМА;
Price текущая цена;
ЕМА_і предыдущее значение ЕМА.
Сглаживающая константа для быстрой ЕМА (fast SC) будет равна 2/(2+1) = 0,66667. В свою очередь, для медленной ЕМА сглаживающая константа (slow SC) составит 2/(30+1) = 0,06452.
Таким образом, нам необходимо получить изменяющуюся сглаживающую константу (scaled smoothing constant, SSC), которая будет принимать значения от 0,66667 до 0,06452, посредством умножения на коэффициент ER. Для этого сделаем следующее преобразование:
SSC = (ER * (fast SC slow SC)) + slow SC или, используя полученные ранее цифры:
SSC = (ER * 0.60215) + 0.06452
Что означает полученная формула? Теперь, если коэффициент ER = 1, сглаживающая константа ЕМА будет равна 0,66667, что соответствует быстрой 2-дневной ЕМА.
В случае если коэффициент ER равен нулю, сглаживающая константа примет значение 0,06452, что будет соответствовать медленной 30-дневной ЕМА. Все промежуточные значения коэффициента ER будут плавно изменять величину сглаживающей константы, регулируя, таким образом, период усреднения ЕМА в зависимости от состояния рынка.
Для более эффективного воздействия полученной изменяющейся сглаживающей константы (SSC) на период усреднения ЕМА Кауфман рекомендует возвести ее в квадрат. Это позволяет увеличить ее влияние на период усреднения ЕМА при очень малых значениях коэффициента ER, то есть на сильно зашумленных участках рынка, со слабой трендовой составляющей.
Таким образом, соединив вместе все полученные результаты, можно записать следующую формулу для адаптивной скользящей средней Кауфмана:
АМА = Price*(SSC"2) + AMA_1 *
(1 SSC'2),
или после преобразования:AMA = AMA_1 + (SSC'2) *
(Price AMA_p
Подставив в приведенную формулу значение SSC, вычисленное посредством коэффициента ER, получим:AMA = AMA_1 + (((ER*0,60215)
+ 0,06452)'2)*(Price AMA_1),
где
ER коэффициент эффективности (Efficiency Ratio);
Price текущая цена.
АМА_1 предыдущее значение АМА.
Рассмотрим динамику движений полученного индикатора на конкретном примере. Предположим, значение вчерашней АМА равняется 40, а сегодняшняя цена равна 47.
На эффективном рынке, когда значение коэффициента ER около единицы, движение АМА в этом случае составит около 3,1 пункта. Это достаточно большая величина почти половина от 7 пунктов разницы.
Если на рынке много шума и слабый тренд, значение коэффициента ER будет значительно меньше единицы. Так, при тех же значениях цены и значении ER = 0,3 движение АМА будет всего около 0,4 пункта.
Таким образом, на эффективном рынке движения индикатора более динамичны и отзывчивы на изменение цены, нежели на рынке с большим количеством шума и слабой трендовой составляющей.
Прииенение АМА Кауфмана в торговых системах
Обычно в торговых системах, построенных на скользящих средних, используются два метода получения торговых сигналов. Первый основан на пересечении ценой индикатора, второй на изменении направления индикатора. Однако, если взглянуть на формулу экспоненциальной скользящей средней, можно обнаружить, что она меняет свое направление именно в момент пересечения ее ценой.
Факт настолько же очевидный, насколько неизвестный многим. Таким образом, простейшей торговой стратегией на основе АМА будет покупка, когда АМА поворачивает вверх, и продажа, когда АМА разворачивается вниз.
Но применение подобной стратегии в лоб приводит к значительному количеству небольших убыточных сделок на ненаправленных участках рынка в условиях так называемой пилы (whipsaw), когда цены совершают многочисленные кратковременные колебания то вверх, то вниз, которые тем не менее не приводят к возникновению пригодных для торговли трендов.
Для того чтобы торговая система на основе АМА перестала реагировать на каждый чих рынка, Кауфман рекомендует использовать дополнительный фильтр. В основе этого фильтра лежит стандартное отклонение (Standard Deviations, StdDev) ежедневных приращений индикатора за определенный период
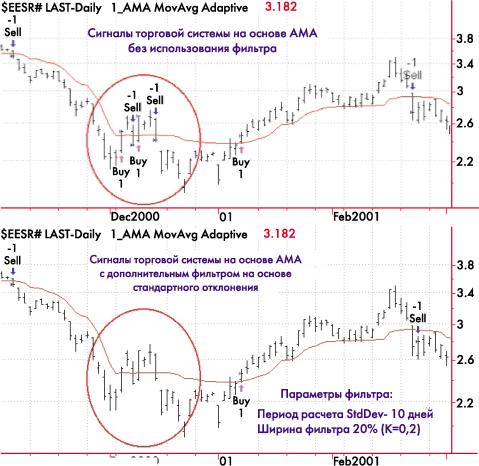
Сигналы торговой системы на основе АМА без использования фильтра (верхний рисунок) и с ис-Рис. 3. пользованием фильтра (нижний рисунок). Обратите внимание на динамику индикатора АМА (красная кривая) в зависимости от состояния рынка
Ьес2000 (обычно тот же период, на котором вычисляется ER).Filter = K*StdDev(AMA AMA_p n),
где
К процентный коэффициент;
n период, на котором вычисляется стандартное отклонение. Таким образом, новые правила для торговой стратегии на основе АМА с фильтром можно выразить следующим образом.
Покупка или продажа происхо-дит тогда, когда текущее движение АМА в нужном направлении от точки разворота превысило на некоторый процент стандартное отклонение ежедневных колебаний АМА за определенный период.
Сигналом к покупке будет следующее условие:
AMA Lowest AMA Filter А условием к продаже, соответственно:
Highest AMA AMA Filter,
где
АМА текущее значение адаптивной скользящей средней;
Lowest AMA минимальное значение АМА в точке разворота снизу вверх;
Highest AMA максимальное значение АМА в точке разворота сверху вниз;
Filter значение фильтра на основе стандартного отклонения движений индикатора.
Для различных рынков Кауфман рекомендует применять разные значения
Приложение
Формула АМА Кауфмана в формате Metastock
Periods:= Input(Time Periods,1,1000, 10);
Signal:= CLOSE Ref(CLOSE,-periods);
Noise:= Sum(Abs(ROC(CLOSE,1,$)),periods);
ER:= Abs(Signal/Noise);
FastSC:= 2/(2 + 1);
SlowSC:= 2/(30 + 1);
SSC:= ER * (FastSC SlowSC) + SlowSC;
Constant:= Pwr(SSC,2);
AMA:= If(Cum(1) = periods+1, Ref(CLOSE,-1) + constant * (CLOSE Ref(CLOSE,-1)),PREV + Constant * (CLOSE PREV));
AMA
Формула АМА Кауфмана в формате Omega TradeStation
Inputs: Period(10);
Vars: Signal(0), Noise(0), Diff(0), ER(0), Smooth(1), Fastest(.6667), Slowest(.0645), AMA(0);
Diff = AbsValue(Close Close[1]);
IF CurrentBar = Period Then AMA = Close;
IF CurrentBar Period Then Begin Signal = AbsValue(Close Close[Period]);
Noise = Summation(Diff, Period);
If Noise 0 then ER = Signal / Noise;
Smooth = Power(ER * (Fastest Slowest) + Slowest, 2);
AMA = AMA[1] + Smooth * (Close aMa[1]);
End;
Plot1( AMA, AMA);
процентного коэффициента К. Так, для торговли фьючерсами или на рынке FOREX подходят небольшие значения фильтра около 10 % (К = 0,1). В свою очередь, для рынков акций необходим более широкий фильтр до 100 % (К = 1).
Несмотря на свою простоту, такой фильтр очень эффективно отсеивает незначительные колебания индикатора на ненаправленных рынках, заметно уменьшая количество ложных торговых сигналов на пиле.
На рис. 3 представлен фрагмент дневных данных РАО ЕЭС (ММВБ). В верхней части рисунка показаны сигналы торговой системы на основе АМА Кауфмана без применения фильтра. В нижней части рисунка представлены сигналы той же системы с использованием описанного выше фильтра.
Хорошо видно, как в сложный для торговли период, в первой половине декабря 2000 года, с помощью предложенного фильтра были отсеяны четыре убыточных сигнала торговой системы. При этом использование фильтра практически никак не отразилось на эффективности прибыльных сигналов.
Таким образом, несмотря на то, что уже в самой методике вычисления АМА Кауфмана заложена адаптация индикатора к текущим рыночным условиям, применение дополнительного фильтра заметно повышает эффективность торговой системы на основе АМА. Это позволяет значительно уменьшить количество убыточных сигналов в моменты, когда рынок находится в состоянии пилы.
В свою очередь, мы можем быть уверены, что настоящие, пригодные для торговли тренды не будут упущены. Торговый сигнал поступит своевременно, на ранней стадии зарождающейся ценовой тенденции.
Заключение
Итак, мы познакомились с еще одним способом адаптации скользящей средней к текущему состоянию рынка. В методе Кауфмана следует выделить два ключевых момента, которые повышают эффективность индикатора и надежность торговых сигналов на его основе. Во-первых, это коэффициент эффективности (Efficiency Ratio), который измеряет относительный уровень шума в ценовых движениях.
Подобная концепция используется и сторонниками теории хаоса в рыночных исследованиях (в их терминологии она называется Fractal Efficiency). Коэффициент эффективности может применяться не только для управления периодом усреднения ЕМА.
С его помощью можно создавать адаптивные ценовые каналы в пробойных торговых системах (Break-Out Systems), регулировать параметры следящего стопа (Trailing Stop) и даже управлять размером позиции (Position Sizing).
Во-вторых, это применение фильтра на основе стандартного отклонения для получения торговых сигналов от индикатора. Причем связка Кауфман стандартное отклонение отнюдь не случайна.
По прошествии лет, мало кто вспоминает, что именно Перри Кауфман в своей книге Новые методы и системы торговли на товарных рынках первым описал применение в торговле каналов на основе стандартных отклонений. Позже эти методы были развиты и дополнены другим известным аналитиком и включены теперь в большинство компьютерных программ для технического анализа под названием полос Боллинджера (Bollinger Bands).
Будучи человеком весьма далеким от математики и всегда шарахаясь как черт от ладана от сложных формул и вычислений, я остановился на описании наиболее простых и доступных методов адаптации скользящих средних. Подходы Ту-шара Шонде и Перри Кауфмана интуитивно понятны и легко реализуемы в компьютерных программах.
Однако нельзя не отметить, что существуют и более навороченные формы фильтрации шумов и уменьшения лагов (запаздываний) в различных индикаторах начиная от Optimal Tracking Filter Джона Элерса (John Ehlers), в котором используются алгоритмы, применяемые в системах наземной и космической навигации, и заканчивая индикаторами от Jurik Research, которые продаются в виде черного ящика за весьма немалые деньги.