Сокол И. - Еще раз об улыбке
В прошлом номере мы выяснили, что улыбка волатильности, как и любой нетривиальный профиль волатильности, изменяет параметр дельта опционной позиции. Правильное определение последнего имеет большое значение в работе с опционами, особенно при торговле волатильностью, когда важную роль играет дельта-хеджирование, соответствующее вашим планам.
Неприятно по окончании торговой сессии обнаружить, что дельта позиции была весь день совсем не такой, на какую вы опирались в своих расчетах. Естественно возникает желание иметь аналитические методы вычисления дельты при наличии произвольного профиля волатильности.
Сразу оговоримся, что волатильностью далее везде по тексту мы будем называть опционную (подразумеваемую) волатиль
ность. Напомним в двух словах, почему канонические методы расчета дельты дают неверный результат при наличии улыбки.
Здесь и далее, когда мы говорим об улыбке волатильности, подразумевается, что наши выводы верны для любого профиля волатильности, а не только для частного случая улыбки. Кроме того, мы считаем, что при смещении цены базового актива вслед за ним смещается и улыбка волатильности.
Это называют плавающим профилем волатильности.
Рис. 1 Смещение профиля волатильности при изменении цены базового актива
ситуации на рынке волатильность опционов с более высокими страйками имеет большее значение, то при росте рынка, по мере приближения стоимости базового актива к ним, опционные волатильности для опционов этих страйков будут снижаться! В качестве примера рассмотрим, как ведет себя стоимость опциона Call при наличии плавающей улыбки волатильности.
В момент времени tt при цене базового актива xt опционная волатильность равна аг (см. рис. 1).
В момент времени t2 при цене базового актива x2, опционная волатильность - а2.
Волатильность опциона изменилась из-за сдвига улыбки вследствие движения базового актива. Мы предполагали, что дальние страйки имеют более высокую волатильность. Это означает, что для страйка, приближающегося к цене базового
Разные способы а хсимации непрерывная аппроксимация кусочно-лине иная аппрокси
Простейшая аппроксимация - отрезками прямой соединяющей точки изображающие значения волатильностей опционов различных страйков.
Производная определяется углом наклона касательной к этой кривой. Причем нас интересует значение производной именно в точках соответствующих страйкам опционов см. рис. 4, то есть как раз там, где наша кривая имеет излом, а ее производная
имеет разрыв. Поэтому будем рассматривать производную в точках излома кривой как полусумму производных справа и слева от точки излома:
д
-Ф) = ((а2 - o^)(s2 - So) + (а0 - o)/(s0 - s))/2.
ds
Если расстояния между страйками одинаковые, то искомая производная в данном приближении дается формулой:
ds
¦ a(s) = ((а2 - Oo)/(s2 - so) + (а0 - a)/(s0 - s))/2 = (аг - o)/(s2 - s) + (o0 - o)/(s2 - s) = (o2 - o)/(s2 - s).
то есть-a(s) = (а2 - a1)/(s2 - s1).
ds актива, волатильность падает. Точнее было бы сказать, что цена базового актива приближается к страйку, но в конечном счете важно лишь то, что расстояние между ними уменьшается.
Если мы имеем дело с плавающим профилем волатильности, а в нашем случае это именно так, то волатильность опциона зависит от расстояния между его страйком и текущей ценой базового актива. То есть профиль волатильности как функцию от страйков опционов можно записать в виде: a(s) = f(x - s).
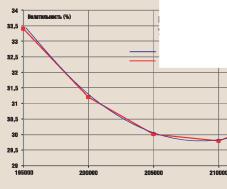
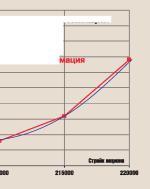
Это обстоятельство принципиально при выводе формулы для параметра дельта, так как именно оно отражает тот факт, что мы имеем дело с плавающим профилем волатильности.
Дельта - это тангенс угла наклона касательной. Канонически рассчитанная дельта это 8 = tg(a).
Как видно на рисунке 1, она сильно отличается от дельты реальной (которую будем обозначать А). Реальная дельта определяется наклоном касательной к кривой изображающей реальное изменение стоимости опциона А = tg(fi).
Подробный вывод формулы для параметра А приведен на врезке Расчет реальной дельты. Сейчас же рассмотрим уже готовый результат:
д
А = 8 - v--a(S) (1)
ds
Здесь используются канонические параметры дельта и вега опциона. Очевидно, что единственной новой величиной является производная от волатильности опциона по его страйку.
Страйки опционов дискретны, и здесь идет речь о производной функции, которая аппроксимирует профиль волатильности.
Вопрос аппроксимации -это отдельная большая проблема. Существуют разные аппроксимирующие функции, мы же сейчас рассмотрим простейшую аппроксимацию улыбки
- отрезками прямой. Это далеко не лучший способ, он не лишен серьезных недостатков. Но в нем есть одно огромное достоинство
- он предельно прост. Для нас же сейчас, при первом знакомстве с данным вопросом, простота способа имеет решающее значение.
Подробнее об аппроксимации см. врезку Аппроксимация улыбки волатильности. Здесь же приведем конечный результат для дельты в случае аппроксимации профиля волатильности отрезками прямой.
Для опциона страйка s0находя-щегося между двумя ближайшими к нему страйками st и s2
РАСЧЕТ РЕАЛЬНОЙ ДЕЛЬТЫ
Предположим, что профиль волатильности, при данной цене базового актива, описывается функцией a(s) = f(x- s), тогда мы можем рассчитать А опциона.
В то время как канонический параметр дельта определяется как частная производная
д
8=-c(x, a)
дх
то есть учитывается только непосредственная зависимость стоимости опциона от цены базового актива, реальный параметр дельта определяется как полная производная от стоимости опциона по цене базового актива, то есть здесь уже учитывается и зависимость опционной волатильности от цены базового актива.
d
А =-c(x, а)
dx
Обратим внимание, что параметр А определяем как полную производную, то есть учитывается не только явная зависимость от х, но и неявная зависимость через а, в отличие от канонического определения параметра дельта, где используется частная производная и соответственно учитывается только прямая зависимость от х.
Раскрывая полную производную, и вспоминая, что a(s) = f(x- s), получаем:
д
Сразу обратим внимание, что-c (x, a) = о,
дx
д
а множитель-c (x, a) = v это просто параметр опционной позиции вега.
дa
Отсюда для параметра А можем написать:
А = 8 - v ¦ a(s) дs
„ д
Значит все, что нам остается для определения реальной дельты позиции, это рассчитать-a
c)s
Рис. 2 Смещение профиля волатильности для опционов на фьючерс Лукойла 18-21 января
где a12 - волатильности страйков st2соответственно,х - цена базового актива, 5 и vканонические параметры опциона дельта и вега.
Заметим, что волатильности 2 будут изменяться при движении цены базового актива х, поэтому при расчетах в каждый момент времени надо брать текущие значения волатильностей at 2.
Альтернативный подход к расчету дельты
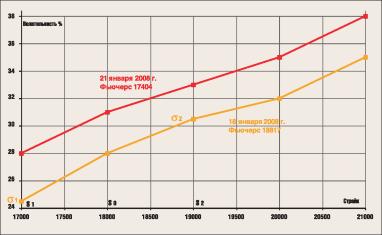
Теперь рассмотрим другой подход, который эквивалентен данному, если функция, аппроксимирующая улыбку волатильности, является достаточно гладкой. Необходимо просто сдвинуть профиль волатильности так, как он сдвигается при движении рынка, и посмотреть, как изменится волатильность и, соответственно, цена опциона.
Ниже приведены технические подробности, но хочется предварительно сделать некоторые замечания по поводу данного подхода.
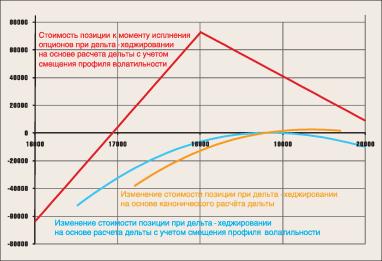
Сразу отметим, что линейная аппроксимация не является достаточно гладкой и при таком подходе дельта для движения рынка наверх или вниз получится разной. В этом состоит отличие от вышеприведенной формулы (2), где в сущности сделано усреднение дельты для движения наверх и вниз. Но зато такой подход со сдвигом профиля волатильности позволяет не только определить дельту, но и построить график зависимости стоимости позиции от цены базового актива.
При этом еще раз обратим внимание, что если аппроксимировать профиль волатильности достаточно гладкой функцией (точнее функцией имеющей непрерывную первую производную), то вышеуказанный недостаток данного подхода исчезнет. А дельта, рассчитанная
таким методом, будет совпадать с дельтой, рассчитанной по формуле (1). Конечно, подразумевается, что и в формуле (1) в качестве профиля волатильности используется та же самая гладкая функция.
Как рассчитать дельту некоторого опциона со страйком s0, сдвигая профиль волатильности?
1. Аппроксимируем профиль волатильности некоторой функцией a(s) = f(x - s), желательно гладкой, но если вы готовы мириться с вышеуказанными недостатками, то можно и отрезками прямой, то есть ломаной линией.
2. Считаем, что текущее значение цены базового актива - x0, текущее значение волатильности рассматриваемого опциона а0 - f(x0 - s0), соответственно цена опциона страйка s0, рассчитанная по формуле Блэка-Шоулза:
С0 = c(x0’ 0).
3. Рассмотрим небольшой сдвиг цены базового актива x0 ^ xt и рассчитаем значение волатильность опциона при цене базового актива xt:
= f(xt - s0).
4. Рассчитаем по формуле Блэка-Шоулза значение цены опциона страйка s0 при цене базового актива xt и при волатильности at:
ct = c(xt fft).
5. Рассчитаем дельту опциона:
А = (ct - C0)/(xt - x0)
Как построить график зависимости стоимости опциона с учeтом смещения профиля волатильности?
1. Аппроксимируем профиль волатильности некоторой функцией a(s) = f(x - s), желательно гладкой, но можно и отрезками прямой, то есть ломаной линией.
2. Рассмотрим сдвиг цены базового актива (не обязательно маленький) x0 ^ x и рассчитаем значение волатильности опциона при цене базового актива xt:
= f(xt - s0).
3. Рассчитаем по формуле Блэка-Шоулза значение цены опциона страйка s0 при цене базового актива xt и при волатильности at:
ct = c(xt fft)-
4. Изменяя значение xt получаем значение стоимости опциона при любой интересующей нас цене базового актива и, соответственно, строим график зависимости стоимости опциона от цены базового актива. Параметры сложной опционной позиции рассчитываем просто как сумму соответствующих параметров отдельных опционов.
Небольшой пример на основе недавних событий
Редкая разновидность профиля волатильности - обратная ухмылка, реализовавшаяся на опционах на фьючерс Лукойла. В качестве примера использования нашей математики рассчитаем изменение дельты опциона страйка 18000 для такого профиля волатильности (см. рис.
2).
Каноническую дельту рассчитываем как обычно, получаем для опциона Put страйка 18000 при цене фьючерса 18817 и волатильности 28%: 8 = -0,32. С учетом же смещения профиля волатильности рассчитаем дельту по формуле (2):
А = 8 - v ¦ (а2 - ffl)/(s2 - s1) = -0,32 -26,8 x (30,5 - 24,5)/(19000 - 17000) ~ -0,32 - 0,08 = -0,4
Волатильность измеряли в процентах (a1 = 30,5%, a2 = 24,5%). Если бы волатильность измеряли в долях единицы (т.е. а1 = 0,305 и а2 = 0,245 соответственно), то параметр вега был бы не v = 26,8, а v = 2680, и конечный результат был бы тем же.
Итак, вместо 8 = -0,32 мы получаем А = -0,4. Это означает, что опционы Put дорожают значительно быстрее, чем можно было ожидать, основываясь на каноническом расчете дельты.
И это ожидаемый результат. Ведь из-за движения профиля волатильности вниз вслед за падением цены базового актива, выросла волатильность опционов страйка 18000. Для покупателей опционов это приятное обстоятельство на падающем рынке.
Для продавцов - при неправильном дельтахеджировании - ровно наоборот, хотя правильный расчет дельты в данном случае помог бы им.
Конечно, с точки зрения трейдера, основное содержание прошедшего периода - движение цены базового актива и изменение уровня волатильности в целом. Но это не уменьшает значения влияния улыбки на параметры позиции, хотя и носит чисто технический характер.
Заключение
Формула Блэка-Шоулза, к сожалению, далека от идеала. Для того, чтобы приблизить ее к реальности, приходится вводить понятие профиля волатильности. Но это приводит к изменению технологии расчета параметров опционной позиции.
В данной статье мы рассмотрели, как аналитически рассчитать параметр дельта при наличии плавающего профиля волатильности, и рассмотрели, как при этом рассчитывать изменение стоимости опционной позиции.
Конечно, все это не более чем технические детали. Никакая математика не заменит правильной стратегии и понимания рынка. Но для реализации своих замыслов эти технические детали иногда оказываются критически важны.
И хотя расчет, например дельты - скучная ежедневная рутина в работе трейдера, торгующего опционами, полезность понимания тонкостей этого процесса часто проявляется на практике. Точнее, непонимание этих тонкостей иногда разрушает самые лучшие замыслы.
Хочется пожелать всем удачи в торгах на рынке опционов, ведь, в конце концов, только на этом рынке заработать могут оба контрагента, участвующе в сделке: и покупатель и продавец! На этой оптимистичной ноте и хочется закончить наше обсуждение.
Удачи в торгах!
