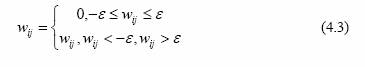|
|

|
|
|
где 2 ij w – синаптический вес, i – номер нейрона, j – номер входа, N – число нейронов, M – размерность входного сигнала нейронов; Метод проекций реализуется следующим образом. Синаптический вес обнуляется, если его значение попало в заданный диапазон
где ε – некоторая константа. Алгоритмы сокращения имеют по крайней мере два недостатка: 1. Нет методики определения числа нейронов скрытых слоев, которое является избыточным, поэтому перед началом работы алгоритма нужно угадать это число. 2. В процессе работы алгоритма сеть содержит избыточное число нейронов, поэтому обучение идет медленно. Предшественником конструктивных алгоритмов можно считать методику обучения многослойных сетей, включающую в себя следующие шаги: 1. Выбор начального числа нейронов в скрытых слоях. 2. Инициализация сети, то есть присваивание синаптическим весами смещениям сети случайных значений из заданного диапазона. 3. Обучение сети по заданной выборке. 4. Завершение в случае успешного обучения; если сеть обучить не удалось, то число нейронов увеличивается, и повторяются шаги со второго по четвертый В конструктивных алгоритмах число нейронов в скрытых слоях также изначально мало и постепенно увеличивается. В отличие от описанной методики, в конструктивных алгоритмах сохраняются навыки, приобретенные сетью до увеличения числа нейронов. Конструктивные алгоритмы различаются правилами задания значений параметров в новых – добавленных в сеть – нейронах: 1. Значения параметров – случайные числа из заданного диапазона; 2. Значения синаптических весов нового нейрона определяются путем расщепления (splitting) одного из старых нейронов. Первое правило не требует значительных вычислений, однако его использование приводит к некоторому увеличению значения функции ошибки после каждого добавления нового нейрона. В ре- зультате случайного задания значений параметров новых нейронов может появиться избыточность в числе нейронов скрытого слоя. Расщепление нейронов лишено двух указанных недостатков. Самым большим недостатком алгоритма является экспоненци- альный рост времени вычислений при увеличении размерности сети. Для преодоления указанного недостатка предлагается упрощенный алгоритм расщепления который не требует значительных вычисле- ний. Кроме описанных способов выбора нейронов для расщепления, может быть использован анализ чувствительности, в процессе кото- рого строятся матрицы Гессе - матрицы вторых производных функ- ции ошибки по параметрам сети. По величине модуля второй произ- водной судят о важности значения данного параметра для решения задачи. Параметры с малыми значениями вторых производных об- нуляют. Анализ чувствительности имеет большую вычислительную сложность и требует много дополнительной памяти. |
Пример применения нейронных сетей в задачах прогнозирования и проблемы идентификации моделей прогнозирования на нейронных сетях 2 |