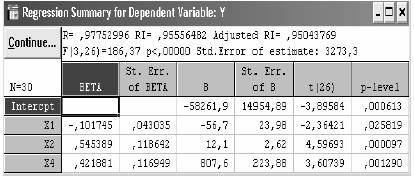
На основе следующего диалогового окна составим уравнение множественной регрессии.

Рисунок 3.14. Суммарная регрессия

 

Уравнение регрессии будет иметь следующий вид

Анализируя данное уравнение, можно сказать, что коэффициенты при первом и втором факторных показателях изменились незначительно, при третьем, последнем факторном признаке коэффициент в уравнении значительно возрос. Поэтому можно сказать, что в

первую очередь на уровень убытков влияет последний фактор – расход сырья на одну тонну халвы, причем при увеличении этого показателя увеличивается и уровень убытков. В меньшей степени на результативный признак влияет процент реализации халвы, и еще

меньше влияет стоимость 1 тонны сырья.

Анализируя остальные показатели, можно сказать, что множественный коэффициент детерминации RI =0,96, что соответствует

предыдущим значениям. Даже притом, что исключались незначимые факторы, число неучтенных факторов так и остается 4%. Важно также отметить, что модель является адекватной, так как FP > FT,

(при степенях свободы v1=3 и v2 = 26 имеем 143,75 > 2,98). На ее

основе можно принимать решения и строить прогнозы. Таким образом, наиболее оптимальным является линейное уравнение регрессии следующего вида

 

---

       

  

---

Линейные многофакторные модели 12