Второй в условиях нестабильности рыночной ситуации и неполном портфеле заказов на год.
Выделение приоритетов необходимо на каждом предприятии и связано в основном с разработкой новых видов продукции на перспективу. В качестве приоритета может выступать переход к энергосберегающим технологиям, поиск средств защиты окружающей среды и т.д. Реализация приоритетов осуществляется путем предоставления режима наибольшего благоприятствования в финансировании программ (проектов, планов).
Комплексность плана обеспечивается при взаимоувязке его составных частей.
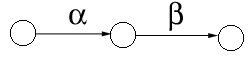
5.3.1. Отношение предшествования (следования)
Как правило, отношение предшествования (следования) задано лишь для нескольких пар работ комплекса, и есть такие пары работ, из которых ни одна не предшествует другой (работы могут выполняться параллельно).
Реально существующие отношения предшествования между работами, событиями комплекса отражаются с помощью ориентированного графа, представляющим собой совокупность элементов двух родов; элементы первого рода именуются вершинами, второго дугами графа. Каждая дуга соответствует определенной паре вершин (дуга соединяет эти вершины, вершины являться граничными для данной дуги). Для каждой дуги указано, какая из двух ее граничных вершин начальная, какая конечная.
По отношению к начальной вершине дуга называется выходящей, а по отношению к конечной входящей.
Путем в графе называется последовательность различных дуг, в которой конечная вершина каждой предыдущей дуги совпадает с начальной вершиной следующей дуги.
Путь называется циклом, если его начало совпадают с концом. Понятию цикла в сетевом планировании соответствует «контур».
Сетью комплекса называется ориентирование граф, отображающий отношения порядка между работами комплекса, Различают два основных типа сетей:
Сети, в которых работам комплекса сопоставлены вершины, а дуги отражают отношения предшествования между работами (сети типа «работы-вершины»)
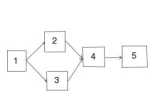
5.3.2. Сетевая модель типа «работы-вершины».
Рисунок 5.3.2 предполагает следующую информацию: работа 1 является исходной и она предшествует работам 2 и 3. Все характеристики работ, такие как продолжительность, стоимость и пр., содержатся в прямоугольнике, а дуга, связывающая прямоугольники вершины, не несет в себе количественных характеристик, а является только связующим звеном.
Работе 4 предшествуют работы 2 и 3. Завершающей работой является работа 5, которой предшествует результат работы 4.
Сети, в которых работам комплекса сопоставлены дуги, а вершины соответствуют некоторым событиям (сети типа «работы-дуги»).
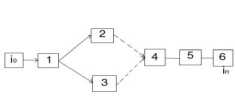
5.3.3. Сетевая модель типа «работы-дуги».
Информация, отображенная на 5.3.3., та же самая, что и на 5.3.2. Но на данной сетевой модели каждая дуга отображает процесс работу и, следовательно, работа (i0 1) является по содержанию той же работой, что и работа 1 на 5.5.2., но вся информационная и количественная характеристика работы лежат на дуге, и таким образом, дуга (i0 1) говорит о том, что работа начинается в событии (точке) i0 и заканчивается событием 1; в свою очередь имеет продолжительность во времени. Далее работы (1-2) и (1-3) начинаются после окончания предшествующей работы (i0 1) и т.д.
Необходимо заметить, что системы кодирования (нумерации) событий отличаются, но смысл процесса, заложенный в данных видах моделей один и тот же.
Целесообразность применения сетей различных типов определяется в каждом конкретном случае особенностями комплекса и характером решаемых задач планирования и управления. Хотя построение сетей типа "работы - вершины" проще, однозначно и не требует введения дополнительных элементов (фиктивных работ), во многих случаях предпочитают сети типа "работы " дуги", поскольку в последних отражены события комплекса. Кроме того, при большом числе входящих и выходящих работ сеть типа "работы - дуги" оказывается более экономной (по числу элементов).
Рассмотрим правила построения сети типа "работы - дуги".Для построения сетевого графика приняты определенные условные изображения и обозначения работ, их результатов и связей между ними.
По своему содержанию и изображению в сетевом графике работа подразделяется (5.3.4) на:
работу, требующую затрат времени и труда (изображается на графике сплошной линией со стрелкой);
фиктивную работу (или связь, зависимость), не требующую затрат времени и труда; показывающую логическую связь между событиями и одновременно указывающую, что возможность начала одной работы зависит от результата другой работы (изображается на графике штриховой линией со стрелкой);
ожидание, или работу, требующую затрат времени, но не требующую затрат труда (изображается на графике линией со стрелкой).
По очередности выполнения все работы, изображаемые сетевом графике, могут быть подразделены на последовательные и параллельные.
Последовательной называется работа, которая может быть начата только после окончания другой, ей предшествующей работы.
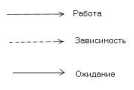
Рис 5.3.4. Изображение работ в сетевом графике.
Параллельными называются работы, которые могут выполняться одновременно после свершения события, обуславливающего возможность их начала. Для правильного отображения связей между работами и событиями, необходимо использовать (работы-связи) фиктивные работы (5.3.5 и 5.3.6).
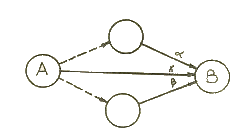
5.3.5. Вариант изображения параллельных работ в сетевом графике с использованием фиктивных работ.
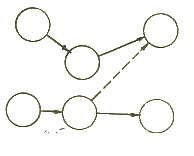
5.3.6. Изображение связи между параллельными и последовательными работами.
При построении сетевого графика могут возникнуть ошибки, некоторые из которых обнаруживаются формальными приемами анализа сетевого графика. В частности, признаками ошибок, допущенных при построении сети, являются циклы (контуры) и тупики (5.3.7).
Из ошибок, для обнаружения которых можно указать формальные правила, наиболее распространенные следующие:
наличие событий не являющихся исходными событиями, и не имеющих входных работ (тупики первого рода событие В на 5.3.7).
наличие событий, не являющихся завершающими (целевыми) событиями и не имеющих исходящих работ (тупики второго рода -. событие А на 5.3.7).
наличие замкнутых путей-контуров (5.3.7).
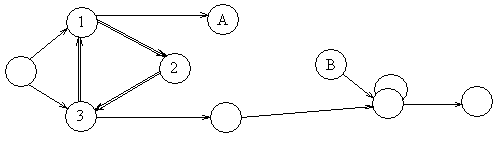
5.3.7. Пример сети с тупиками и контурами.
Ошибки типа неправильно указанного номера события не противоречат основным правилам построения сетей (если они не приводят к появлению тупиков и контуров), поэтому для них нельзя построить формальные правила обнаружения, и они могут быть устранены только путем тщательного просмотра исходных данных модели.
Наличие контура свидетельствует об искажении отношений порядка между работами, входящими в цикл (контур), поскольку каждая из этих работ оказывается предшествующей самой себе и любой другой из работ, образующих цикл, чего не может быть в реальности.
Тупики в сети могут появиться, например, в результате того, что:
в исходной информации о сети пропущены некоторые работы;
в сеть внесены события и работы, которые не являются необходимыми для достижения целей моделируемого комплекса.
Все ошибки (тупики и контуры) должны быть устранены.
Таким образом, сетевая модель будет иметь следующий вид (5.3.8.)
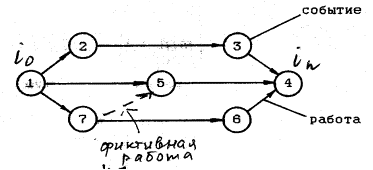
5.3.8. Сетевая модель
Можно сформулировать основные свойства работ и событий сетевой модели:
1. Событию непосредственно предшествует, по крайней мере, одна работа и, по крайней мере, одна следует за ним (за исключением исходного и завершающего).
2. Ко всем работам, имеющим своим началом некоторое событие, можно приступить только тогда, когда окончены все непосредственно предшествующие ему (событию) работы.