Прогнозирование сезонных явлений
2) сложность подбора уравнения регрессии. Эта проблема разрешима при использовании типовых компьютерных программ.
3. Оценка точности прогнозов, построенных методами
экстраполяции
Точность прогноза – это важнейшая его характеристика. Существует несколько способов оценки точности прогнозов:
1) средняя абсолютная оценка:
где n – число уровней временного ряда;
2) средняя квадратическая оценка:
Чем ближе к нулю первый и второй показатели, тем выше точность прогноза;
3) средняя относительная ошибка:
=
Интерпретация значений средней относительной ошибки для оценки точности прогнозов:
| , % |
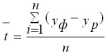
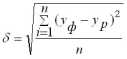
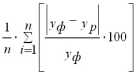
Интерпретация |
| 10 |
Точность прогноза высокая |
| 10-20 |
Точность хорошая |
| 20-50 |
Точность удовлетворительная |
| 50 |
Точность неудовлетворительная |
4. Прогнозирование сезонных явлений
К сезонным относят такие явления, которые обнаруживают в своем развитии определенные закономерности, регулярно повторяющиеся из месяца в месяц, из квартала в квартал.
Под сезонностью также понимают неравномерность производственной деятельности в отраслях промышленности, связанных с переработкой сельскохозяйственного сырья, поступление которого зависит от времени года. Кроме того, сезонность может возникать из-за сезонного характера спроса на товары, производимые промышленностью, реализуемые торговлей, и т.д.
Исследование сезонности с целью разработки прогноза ставит следующие задачи: численно выразить проявление сезонных колебаний; выявить их силу и характер в условиях отдельных отраслей экономики; вскрыть факторы, вызывающие сезонные колебания; найти экономические последствия проявления сезонности.
Методика прогнозирования сезонного явления следующая:
1. Представить графически фактические значения изучаемого явления, чтобы выяснить, присутствует ли сезонная волна, выявить характер тренда.
2. Рассчитать показатели сезонности (4-квартальные суммы, 4- квартальные средние, центрированные средние, показатели сезонности).
3. Определить индексы сезонности.
4. Вычислить параметры уравнения, описывающего тренд изучаемого явления.
5. Построить прогноз, вычислить его ошибку.
Примеры решения контрольных заданий
Задание 1. Имеются данные использования ВВП за 1992-1999 гг. (трлн. руб.)
| 1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
| Использование ВВП |
19,6 |
101,0 |
171,5 |
348,6 |
493,2 |
610,7 |
701,3 |
875,4 |
1. Постройте прогноз использования ВВП на 2000 г., используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте среднюю относительную ошибку полученных прогнозов при использовании каждого метода.
4. Сравните результаты.
Решение.
1. Метод скользящей средней. Для того, чтобы рассчитать прогнозное значение необходимо
1. Определить величину интервала сглаживания, например равную 3 (n = 3).
2. Рассчитать скользящую среднюю для первых трех периодов
m 1993 = (У1992 + У1993 + У 1994)/ 3 = (19,6+101,0+171,5)/3 = 97,4
Полученное значение заносим в таблицу в средину взятого периода.
Далее рассчитываем m для следующих трех периодов 1993, 1994, 1995 гг.
m 1994 = (У1993 + У1994 + У 1995)/ 3 = (101,0+171,5+348,6)/3 = 207,0
далее по аналогии рассчитываем m для каждых трех рядом стоящих периодов.
Для решения задачи составим таблицу
| Годы |
Использова-ние ВВП, трлн. руб. Уt |
Скользящая средняя m |
Расчет средней отно-сительной ошибки /Уф - Ур/ Уф * 100 |
| 1992 1993 1994 1995 1996 1997 1998 1999 |
19,6 101,0 171,5 348,6 493,2 610,7 701,3 875,4 |
- 97,4 207,0 337,8 484,2 601,7 729,1 - |
- 3,6 20,7 3,1 1,8 1,5 4,0 - |
| Итого |
34,7 |
||
| прогноз 2000 2001 |
787,1 758,5 |
3. Рассчитав скользящую среднюю для всех периодов строим прогноз на 2000 г. (см. формулу 1).
У2000 = 729,1 + 1/3 (875,4 – 701,3) = 729,1 + 58,03 = 787,1
Определяем скользящую среднюю m для 2000 года.
m = (701,3+875,4+787,1) /3 = 787,9
Строим прогноз на 2001 г.
У 2001 = 787,9 + 1/3 (787,1-875,4) = 758,5
Заносим полученный результат в таблицу.
Рассчитываем среднюю относительную ошибку (см. формулу 10)
= 34,7/6 = 5,8
2. Метод экспоненциального сглаживания.
Определяем значение параметра сглаживания (см. формулу 3).
2/ n+1 = 2/ 8+1 = 0,2
Определяем начальное значение Uo двумя способами:
1 способ (средняя арифметическая) Uo = 3321,3/8 = 415,2
2 способ (принимаем первое значение базы прогноза) Uo = 19,6
Расчетная таблица
| Годы |
Использова-ние ВВП, трлн. руб. У t |
Экспоненциально взвешенная средняя Ut |
Расчет средней относительной ошибки |
||
| I способ |
II способ |
||||
| I способ |
II способ |
||||
| 1992 1993 1994 1995 1996 1997 1998 1999 |
19,6 101,0 171,5 348,6 493,2 610,7 701,3 875,4 |
415,2 336,1 289,1 265,6 282,2 324,3 381,6 445,6 |
19,6 19,6 35,9 63,0 120,1 194,7 277,8 362,6 |
20,2 23,3 68,6 23,8 42,8 46,7 45,6 49,1 |
0 80,6 79,1 81,9 75,6 68,2 60,4 58,6 |
| Итого |
3321,3 |
2739,7 |
1093,3 |
320,1 |
504,4 |
| прогноз 2000 |
531,6 |
464,9 |
|||
Рассчитываем экспоненциально взвешенную среднюю для каждого года, используя формулу 2.
U1992 = 19,6*0,2 +(1-0,2) * 415,2 = 336,1 1 способ
U1993 = 101*0,2+(1-0,2) * 336,1 = 270,9 1 способ и т.д.
U1992 = 19,6*0,2 +(1-0,2) * 19,6 = 19,6 II способ
U1993 = 101*0,2+(1-0,2) * 19,6 = 35,9 II способ
U1994 = 171,5*0,2+(1-0,2) * 35,9 = 63,0 II способ и т.д.
Рассчитываем прогнозное значение, используя формулу 2.
U 2000 =875,4*0,2 + 0,8*445,6 = 531,6 (I способ)
U 2000 =875,4*0,2 + 0,8*362,6 = 464,9 (II способ)
Средняя относительная ошибка (см. формулу 10)
= 320,1/8 = 40,01% (I способ)
= 504,4/8 = 63,05% (II способ)
3. Метод наименьших квадратов.
Для решения используем следующую таблицу.
| Годы |
Иполь-зовние ВВП, трлн. руб. Уф |
Условное обо-значение времени Х |
Уф*Х |
Х^2 |
Ур |
Расчет средней относительной ошибки / Уф - Ур/ Уф * 100 |
| 1992 1993 1994 1995 1996 1997 1998 1999 |
19,6 101,0 171,5 348,6 493,2 610,7 701,3 875,4 |
1 2 3 4 5 6 7 8 |
19,6 202,0 514,5 1394,4 2466,0 3664,2 4909,1 7003,2 |
1 4 9 16 25 36 49 64 |
-20,6 103,9 228,4 352,9 477,4 601,9 726,4 850,9 |
2,05 2,87 33,17 1,23 3,20 1,44 3,58 2,8 |
| Итого |
3321,3 |
36 |
20173 |
204 |
3321 |
50,32 |
| прогноз 2000 2001 |
975,4 1099,9 |
9 10 |
Определим условное обозначение времени как последовательную нумерацию периодов базы прогноза. Рассчитаем графы 4 и 5.
Ур определим по формуле 4, а коэффициенты a и b по формулам 5 ,6.
20173 - (36 * 3321,3) / 8
a = 204 - 36^2 / 8 = 124,5
b = 3321,3/8 – 124,5*36/8 = - 145,1
У1992 = 124,5*1 – 145,1 = -20,6
У1993 = 124,5*2 – 145,1 = 103,9 и т.д.
Заносим полученные результаты в таблицу. Определяем прогнозное значение.
У 2000 = 124,5*9 – 145,1 = 975,4
У 2001 = 124,5*10 – 145,1 = 1099,9
Рассчитываем среднюю относительную ошибку (см. формулу 10)
= 50,32/8= 6,29%
Сравните полученные результаты по прогнозам разработанным различными методами и средней относительной ошибке. Сделайте вывод какой метод позволил получить более достоверные результаты
Задание 2.
В таблице представлен объем продаж товара А в городе.
Постройте график исходных данных и определите наличие сезонных колебаний.
Постройте прогноз объема продажи товара А в городе на 2002 гг. с разбивкой по кварталам.
Рассчитайте среднюю относительную ошибку прогноза.
Решение.
1. Представим исходные данные графически. По оси Х отложим параметр времени (годы и кварталы), а по оси У объем продаж. Определим наличие сезонных колебаний.
2. Составим таблицу (см. ниже).
3. 4-х квартальные суммы рассчитываются суммированием Уф за четыре рядом стоящие квартала.
42,2+55,4+64,8+63,4 = 225,8
55,4+64,8+63,4+48,1 = 231,7 и т.д.
4-х квартальные средние = 4-х квартальные суммы/4 = 225,8/4 =56,45; 231,7/4 = 57,93. В таблице они ставятся в средину суммируемых кварталов.
Центрированные средние рассчитываются как сумма двух 4-х квартальных средних деленная на 2, например
(56,45 + 57,93) / 2 = 57,19; (57,93 + 58,50) / 2 = 58,2 и т.д.
4. Определяем показатели сезонности.
Псезон= Уф / Центр.средние * 100 (или графа 3/на графу 6 * 100).
Так, для 3 квартала 1999 г. Псезон = 64,8 / 57,19 * 100 = 113,31
Для 4 квартала 1999 г. Псезон = 63,4 / 58,21 * 100 = 108,91 и т.д.
Определим индексы сезонности для каждого квартала ( I j ) . Для расчета берутся показатели сезонности, суммируются по квартально и делятся на количество суммированных значений.
Для 1 квартала I 1 = (81,4 + 77,3) /2 = 79,35
Для 2 квартала I 2= (95,8 + 98,8) /2 = 97,3
Для 3 квартала I 3= (113,3 + 115,2) /2 = 114,25
Для 4 квартала I 4= (108,9 + 110,5) /2 = 109,7
6. Определяем в таблице графы 8,9,10.
7. Ур = a * X + b , коэффициенты a и b рассчитываются по формулам 5 и 6.
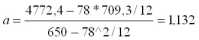
Год |
Квартал |
Объем продаж млн.руб Уф |
Показатели сезонности |
Условное обозначе ние вре мени, Х |
Х^2 |
Уф*Х |
Ур |
Расчет средней относи тельной ошибки |
|||
| 4-квар- таль- ные суммы |
4-квар- таль- ные средние |
Центри рован- ные средние |
Показатели сезон ности |
||||||||
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 1999 2000 |
1 2 3 4 1 2 3 4 |
42,2 55,4 64,8 63,4 48,1 57,7 69,7 67,1 |
- - - 225,8 231,7 234 238,9 242,6 |
- 56,45 57,93 58,5 59,73 60,7 60,4 |
- - 57,19 58,2 59,1 60,2 60,5 60,7 |
- - 113,3 108,9 81,4 95,1 115,2 110,5 |
1 2 3 4 5 6 7 8 |
1 4 9 16 25 36 49 64 |
42,2 110,8 194,4 253,6 240,5 346,2 487,9 536,8 |
52,88 54,01 55,15 56,28 57,41 58,54 59,67 60,81 |
25,31 2,51 14,89 11,23 19,36 1,46 14,39 9,37 |
- Прогнозирование национальной экономики
- Прогностика - это наука о закономерностях разработки прогноза.
- Анализ объекта прогнозирования начинается с описания.
- Формализованные методы прогнозирования
- Интуитивные методы прогнозирования
