При расчете различных степенных средних все основные показатели, на основе которых осуществляется этот расчет (m, п), остаются неизменными. Меняется только величина т и соответственно.
Средняя геометрическая величина используется в юридической статистике в основном для определения темпов роста, например, преступлений.
Среднегодовой темп роста преступлений будет рассчитываться по следующей формуле:
Хгеом = Пх1 Х2 Х3 - Хп ,
где x1,x2,х3, хп - годовые темпы роста; п - число лет в периоде, за который исчисляется средняя геометрическая, не считая базового года.
Средний геометрический показатель может также быть получен на основе следующей формулы
геом
где Уп - абсолютный уровень конечного года; Уб - абсолютный уровень базового года; п - число лет (без учета базового года).
Модой в статистике называется значение признака (варианта), которое чаще всего встречается в данной совокупности. Обозначим ее символом Мо и определим в вариационном ряду юридически значимых показателей.
Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака.
Для расчета моды интервального ряда используется следующая формула
/Mo /1
fj )+/fMo
Мо = X 0
C/M
где X0 - минимальная граница модального интервала; i - значение модального интервала; /Мо - частота модального интервала; /1 - частота интервала, предшествующего модальному; /2 - частота интервала, следующего за модальным.
Медианой в статистике называется варианта, которая находится в середине ранжированного ряда. Медиана делит упорядоченный ряд пополам. По обе стороны от нее находится одинаковое число единиц совокупности.
Медиана обычно обозначается символом Ме.
Для расчета медианы интервального ряда используется следующая формула:
Me = X 0
Me
где X0 - минимальная граница медианного интервала; i - значение модального интервала; /- сумма всех частот; SXо - сумма накопленных частот, предшествующих медианному интервалу; /Ме - частота медианного интервала.
1 Размах вариации:
2 Дисперсия:
xmin -
max
Х/х - x )2
п
3 Среднее квадратическое отклонение:
| ст = | 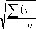 |
х) 2 |
4 Коэффициент вариации:
V = ст - 100 % х
где ст - среднее квадратическое отклонение; х - средний арифметический показатель.
Коэффициент вариации является критерием типичности средней. Если он относительно большой (например, выше 40 %), то это значит, что типичность такой средней очень невысока.
И наоборот, если его значение малое, то средняя является типической и надежной.
1 Что такое средняя величина и каково ее значение в изучении материалов юридической статистики?
2 Приведите классификацию средних величин.
3 В чем отличие между простой средней величиной и средневзвешенной величиной?
4 С использованием какой средней величины рассчитывается среднегодовой темп роста преступлений?
5 Для каких целей в статистике используются мода и медиана?
1 Статистика преступлений, совершенных в 2002 году в городе Мичуринске показывает, что случаев: хулиганства зафиксировано - 200, мошенничества - 100, убийств - 30, грабежей - 80, краж - 150. Необходимо найти размах вариации R и среднее значение количества преступлений X, а также какую часть среди общего количества преступлений составляют грабежи.
2 Определить среднегодовой темп роста количества убийств в
г. Мичуринске в период с 1995 по 1999 г., если известно, что в 1995 г. было совершено 20 убийств, в 1996 г. - 30, в 1997 г. - 45, в 1998 г. - 65,
в 1999 г. - 70.
3 Определить моду и медиану для следующего интервального ряда данных.
| Возраст | Количество |
| преступников, лет | преступлений |
| 17 - 27 | 800 |
| 28 - 38 | 1000 |
| 39 - 49 | 700 |
| 50 - 60 | 400 |
| Более 61 | 100 |
| Итого: 3000 |
Теория выборочного наблюдения базируется на статистических закономерностях, которые формируются и обнаруживаются в массовых явлениях и процессах. Это свойство закономерностей получило название закона больших чисел.
Математической основой закона больших чисел, да и статистической науки в целом, служит теория вероятностей, представляющая собой раздел математики, в котором изучаются случайные явления (события), имеющие устойчивую частость, а следовательно, и вероятность, что помогает выявлять закономерности при массовом повторении явлений.
Исходя из закона больших чисел, чем больше изученная сово-купность случайных явлений, тем должно быть более упорядоченным распределение полученных данных.
Упорядоченность изменения случайных вели/ ін называется закономерностью распределения и графически представляется с помощью гистограммы или полигона распределения. Гистограмма, или полигон распределения, представляет собой ломаную кривую, характеризующую фактическое распределение полученных данных. Она позволяет выявить лишь приближенную картину распределения всей (генеральной) совокупности.
Чем больше выборочное изучение, тем в большей мере будут сглаживаться влияние случайных причин и явственнее проступать действительная закономерность распределения. В этом случае кривая распределения фактических данных будет приближаться к теоретической кривой распределения.
В математической статистике теоретическую кривую распределения обычно называют кривой Лапласа-Гаусса, или нормальным распределением.
Распределение данных наиболее полно характеризуется следующими параметрами: размахом вариации и отклонением от среднего арифметического значения.
Размах вариации (колебаний) - наиболее простой параметр измерения разброса значений варьирующего признака. Он исчисляется по формуле
R = xmax - Хщіп. При одном и том же размахе вариации совокупности данных могут существенно различаться по структуре, т.е. быть более или менее однородными.
Средняя арифметическая величина рассчитывается по следующей формуле
_ x + x2 + x3 +... + xn
X =-2-3-- ,
n
где xi, x2, ..., xn - значения показателей; n - число значений.
Вместо средней арифметической можно использовать также средневзвешенную величину:
x = xifi + x2 f2 + x3f3 + - + xnfn
взв = ? f ’
где fi, f2, ..., fn - частоты появления показателей.
Средняя арифметическая лежит в основе расчета дисперсии (колеблемости), которая представляет собой не что иное, как значение отклонения всех вариант от средней. Значение дисперсии и предопределяет объем выборочной совокупности.
Чем больше дисперсия, тем больше разброс показателей от средней, а следовательно, нужен больший объем выборки, чтобы она была достаточно репрезентативной.
Дисперсия - это средний квадрат отклонения изучаемого признака от теоретического (среднего) показателя. Она характеризует уровень однородности исследуемой совокупности и обозначается символом а2 (сигма малая в квадрате).
Определение объема и представительности выборочной совокупности, а следовательно, и дисперсии производится применительно не к преступности, административной правонарушаемости или другим социально-правовым явлениям вообще, а лишь к их конкретным показателям. Последние могут быть качественными, или атрибутивными (вид преступления, содержание мотива, свойства личности и т.д.) и количественными (возраст правонарушителей, уровень образования, повторность совершения преступления, сроки рассмотрения гражданских дел и т.п.). Каждый признак имеет свою дисперсию, а следовательно, и необходимый объем выборки для надежного изучения.
Это значит, что при выборочном изучении многих признаков, чтобы выявить совокупные отклонения, дисперсию надо рассчитывать по каждому из них. Иногда эти признаки исчисляются десятками и даже сотнями. Чтобы избежать множества расчетов, можно ограничить их только в отношении тех признаков, на базе которых делаются основные выводы.
Общая численность выборки или ее общая репрезентативность определяются по совокупной представительности всех параметров.
При наличии удельного веса качественного признака его дисперсия рассчитывается по следующей формуле
а2 = Р (1 - Р),
где Р - доля качественного признака, а (1 - Р) - доля иных признаков или противоположного признака. Дисперсия количественного признака рассчитывается по формуле:
а2 = X(x ~ X)2 f = (х1 - X)2 fi + ( - х)2 f2 + (xt - х)2 /з + ... + (*! - X)2 fn X f f1 + f2 + f3 + - - - + fn
где а2 - дисперсия; x1, x2, ..., xn - значения признаков; х - среднее арифметическое значение признака; f1, f2,..., fn - частоты появления признаков.
Извлекая корень квадратный из дисперсии, получаем среднее квадратическое отклонение:
а = Vp(1 - p) - для качественных признаков;
X(x - х )2 f
X f
а2 =
для количественных признаков.
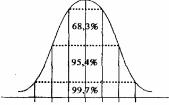
6).
При выборочном наблюдении регистрируется только часть единиц генеральной совокупности. Но эта часть по объему должна быть такова, чтобы получаемые сведения оказались репрезентативными, т. е. достаточно верно отражали содержание и закономерности изучаемого явления в целом.
Под репрезентативностью понимается свойство выборочной совокупности воспроизводить характеристики генеральной совокупности.
Разность между данными генеральной и выборочной совокупностей называют ошибкой репрезентативности, или ошибкой выборки.
Ошибки бывают тенденциозными (систематическими) и случайными. Первые - результат неправильного или преднамеренного отбора исследователем тех или иных показателей, вторые - результат случайностей неполного отбора.
Формула для вычисления ошибки выборки в общем виде выглядит так: где W - ошибка выборки; а2 - дисперсия; а - среднее квадратическое отклонение; п - число единиц выборки.
Подставляя значение дисперсии в формулу ошибки выборки для качественного и количественного признаков, получим:
P(1 - P).
5
П
I(x - x )2 fIf
Все предшествующие формулы и расчеты ошибки репрезентативности имеют значение для повторной выборки. При ней каждая отобранная из генеральной совокупности единица (например, статкарта на преступление) вновь возвращается в массив. Поэтому не исключена возможность ее повторного отбора. Наряду с таким отбором есть отбор бесповторный.
При нем каждая отобранная единица исключается из числа единиц генеральной совокупности, а поэтому может попасть в выборку лишь один раз. В связи с этим ошибка выборки для качественных и количественных признаков вычисляется соответственно по разным формулам:
1 Что такое выборочное наблюдение и каковы его отличия от других видов статистического наблюдения?
2 Какова математическая основа выборочного наблюдения?
3 В чем заключается правило трех сигм?
4 Что понимается под ошибкой выборки?
5 Приведите формулы для расчета различных видов ошибок выборки (для повторной и бесповторной выборки по качественному и количественному признакам).
1 Рассматривается 100 уголовных дел, по которым вынесен приговор. Среди общего количества осужденных: 15 человек получили - 3 года лишения свободы, 20 человек - 4 года, 30 человек - 5 лет, 25 человек - 6 лет, 10 человек - 7 лет.
Необходимо определить: а) средневзвешенное значение сроков наказания; б) дисперсию и ошибку выборки количественного признака сроков наказания; в) дисперсию и ошибку выборки качественного признака при условии, что 10 % среди общего количества преступлений было совершено в состоянии алкогольного опьянения; г) величину выборки количества преступлений при ошибке выборки W = 0,1 для количественного признака и W = 0,02 для качественного признака.
2 При проведении опроса на улицах г. Тамбова по поводу возобновления смертной казни было опрошено 2 тыс. человек, среди которых 50 % высказались за возобновление смертной казни. Необходимо определить ошибку выборки, если известно, что приблизительная численность взрослого населения Тамбова 300 тыс. чел.
3 При проведении опроса на улицах г. Тамбова по поводу возобновления смертной казни было опрошено определенное количество человек, среди которых 50 % высказались за возобновление смертной казни. Необходимо определить количество опрошенных людей или величину выборки, если известно, что приблизительная численность взрослого населения Тамбова равна 300 тыс. чел., а погрешность выборки должна составлять 1 %.
В судах, органах прокуратуры, внутренних дел, налоговой полиции, таможенной службы, адвокатуре, нотариате и других государственных и общественных юридических учреждениях ведется многолетний непрерывный государственный и ведомственный учет преступности, судимости, административной правонарушаемости, гражданско-правовых споров, рождений, браков, смертей и других юридически значимых явлений. Это дает возможность по накопленным в течение десятков лет данным выявлять и отслеживать происходящие изменения во времени многих тысяч
различных статистических показателей. Ежедневный, ежемесячный и ежегодный сбор огромного статистического материала был бы абсолютно неоправданным, если его всесторонне не анализировать по вертикали (структура, состояние, взаимосвязи) и по горизонтали (тенденции, динамика, сезонность), назад (ретроспектива, интерполяция) и вперед (экстраполяция, прогноз).
Анализ динамики юридически значимых явлений за длительный период времени дает возможность понять их развитие в прошлом, настоящем и возможном будущем, оценить эффективность деятельности юридических учреждений и спланировать ее на перспективу.
Основная тенденция в изменении явлений во времени в статистической литературе, особенно зарубежной, нередко именуется трендом. Характер тренда изучаемого явления иногда очевиден при первом ознакомлении с динамическими рядами абсолютных показателей.
Но чаще всего тенденции и закономерности развития явления проявляются в процессе различных преобразований рядов динамики с использованием относительных и средних величин.
Грамотный статистический анализ рядов динамики - залог объективных выводов об изучаемых статистических явлениях. Ряды динамики, или временные ряды, представляют собой ряды числовых значений конкретных статистических величин за какой-то определенный отрезок времени (месяц, квартал, год, пятилетка и т.д.).
В ряду динамики имеются два основных показателя: показатель времени (шкала времени) и уровень ряда (шкала уровня ряда). Уровень ряда, обычно обозначаемый символом У, изначально выражен в абсолютных показателях, на основе которых в процессе аналитической работы рассчитывается множество производных обобщающих величин, относительных и средних.
Наглядно ряды динамики, как правило, излагаются в виде хронологических таблиц и графиков. В последних шкалы времени обычно располагаются на оси абсцисс, а шкалы уровня ряда - на оси ординат. В зависимости от вида приводимых в динамических рядах обобщающих показателей их делят на ряды динамики абсолютных, относительных и средних величин. По характеру отражения реалий ряды динамики делятся на моментные и интервальные, которые в свою очередь могут иметь множество разновидностей: ряды темпов роста, темпов прироста, коэффициентов, индексов, средних квадратических отклонений, дисперсии и т.д.
Многие из этих показателей в той или иной мере рассматривались нами в главах об абсолютных, относительных и средних величинах. В данной главе, специально посвященной рядам динамики, предстоит изложить интегральные особенности динамических рядов тех или иных величин.
Моментные ряды характеризуют уровни изменения юридически значимых явлений на определенные моменты времени (дата учета), например, на начало месяца, квартала, года или по состоянию на 1 января,
30 июня, 31 декабря и т.д. Типичные моментные ряды в юридической статистике - количество заключенных в колониях, тюрьмах, следственных изоляторах или число судей, прокуроров, следователей, адвокатов, юрисконсультов в учреждениях, регионе, стране, взятые на какую-то дату за несколько лет.
Период между датами в моментных рядах называется интервалом ряда. Он может быть годовым, квартальным, месячным.
Особенностью моментного ряда является то, что его показатели, раскрывая то или иное состояние, не могут суммироваться или укрупняться. Число судей, числящихся по состоянию на 1 января 1997 г., нельзя суммировать с числом судей, числящихся на I июля, т.е. на начало второго полугодия данного года, или на 1 января 1998 г., поскольку это могут быть одни и те же штатные единицы, если даже общее число судей как-то изменилось (некоторые судьи уволились или перешли на другую работу, а на их место или на вновь открывшиеся вакансии пришли новые).
Интервальные ряды характеризуют величину изучаемого показателя, полученного за какой-то период времени (интервал). В моментном ряду интервал - промежуток времени между датами учета сведений, а в интервальном ряду интервал - тот же промежуток времени, но за который обобщены приводимые сведения, когда они накапливались. Поэтому месячные данные можно суммировать по кварталам, квартальные - по годам, годовые - по пятилетиям и т. д. В моментном ряду величина уровня ряда не зависит от размера интервала. И на начало каждого месяца, и на начало каждого года общее число сотрудников прокуратуры в городе N может быть одним и тем же.
В интервальном ряду величина уровня ряда существенно зависит от размера интервала. Число учтенных преступлений за год может быть (примерно) в 12 раз больше, чем за любой из его месяцев.
Иногда говорят, что моментный ряд учитывает состояние на какой-то момент, а интервальный ряд отражает деятельность (совершение преступлений, борьба с преступностью, установление юридических фактов и т. д.), сведения о которой характеризуются накопительностью.
На основе рядов динамики абсолютных величин в моментном и интервальном рядах могут быть получены ряды динамики относительных и средних величин, что дает возможность многократно увеличить аналитические возможности динамических рядов. Ряды динамики, выраженные в относительных величинах (процентах, долях, коэффициентах, индексах) или в средних величинах (средней арифметической, средней геометрической, среднем квадратическом отклонении, дисперсии) иногда именуются динамическими рядами обобщающих величин.
Это не совсем точно, поскольку суммарные абсолютные показатели, на основе которых рассчитываются относительные и средние величины, тоже являются величинами обобщающими.
Динамические ряды могут состоять из какого-то n числа варьирующих уровней, которые как всякая статистическая совокупность могут быть выражены в тех или иных показателях.
Наиболее распространенные показатели - это абсолютный прирост или снижение (разность между последующими и предыдущими абсолютными суммарными величинами), темпы роста или снижения (изменения уровня ряда в процентах по сравнению с постоянным базовым показателем или переменным показателем предыдущего уровня), среднегодовые темпы прироста или снижения (средняя геометрическая величина годовых темпов роста или снижения). Наряду с указанными показателями в динамическом ряду может быть рассчитан средний уровень ряда.
Он применим для любого ряда динамики, интервального и моментного, абсолютных, относительных и средних величин.
Для любых интервальных рядов, для интервальных и моментных рядов средних величин средний уровень ряда рассчитывается по правилам средней арифметической:
nI У
У = 1=0
J V
n
где У1 - 1-й - годовой уровень; i = 1, ..., n - число уровней.
Наличие среднего уровня ряда динамики позволяет рассчитывать среднее квадратическое отклонение отдельных уровней от общей средней (а), а также коэффициент вариации (V).
Оперируя этими показателями, особенно в сравнительных исследованиях, можно найти отличительные характеристики, которые при обычных сравнениях сопоставляемых динамических рядов не так очевидны.
В юридической статистике не так часто можно встретиться с плавно меняющимися или неизменными уровнями рядов динамики, особенно в наше сложное в правовом отношении время. Уровни динамики имеют заметные колебания.
Эти колебания показателей динамики связаны с непоследовательностью проведения правовой реформы, недостаточным правовым обеспечением процессов переходного периода, противоречивостью действующего законодательства, формированием новых юридических подходов и многими другими причинами.
В условиях большой колеблемости показателей динамических рядов очень важно выявить три компонента динамики: 1) основные тенденции, выражающие долговременные изменения; 2) систематические, но кратковременные изменения; 3) несистематические случайные колебания, которые часто обусловлены субъективными и иными частными причинами.
Необходимость отделения наносного, случайного и временного от устойчивого и закономерного в уровнях динамических рядов диктуется потребностями изучения основных тенденций и закономерностей развития того или иного явления. С этой целью уровни рядов динамики подвергают различным математическим преобразованиям, которые позволяют выявить главные изменения уровней ряда.
Смыкание динамических рядов имеет особую актуальность в юридической статистике. Изменения законодательства, принципов и форм учета не позволяют дать единый динамический ряд сопоставимых показателей.
Например, некоторое время в УК РСФСР был один перечень тяжких преступлений, в 1994 г. его существенно расширили, а в 1997 г., после вступления в силу УК 1996 г., принципиально изменили. В этих условиях обычный ряд динамики тяжких преступлений за 1991 - 1997 гг. не может быть составлен, так как имеющиеся данные несопоставимы.
Аналогичные трудности возникают при изменении единиц учета, территории и при других основаниях несопоставимости. Чтобы выявить общую тенденцию изменения уровня тяжких преступлений, можно осуществить смыкание рядов динамики.
Покажем это на конкретном примере.