Понятие динамического равновесия в экономике. Простейшая модель равновесия

В экономической теории важным является понятие равновесия, то есть такого состояния объекта, которое он сохраняет при отсутствии внешних воздействий. Задачи экономической динамики включают как описание процессов выхода к состоянию равновесия, так и процессов трансформации самого этого состояния под воздействием внешних сил.

Рассмотрим простую экономическую систему в состоянии равновесия и опишем движение такой системы в непрерывном и дискретном случаях. В первом случае динамика системы описывается с помощью дифференциального уравнения, во втором — разностного уравнения.

Дифференциальное уравнение связывает изменения показателя х со скоростью его движения х

или х Будем считать, что скорость изменения показателя х пропорциональна величине его отклонения от равновесного значения хе. Иными словами, чем дальше показатель отклонился от равновесного значения, тем быстрее он стремится вернуться к нему.

Если в уравнении присутствует только первая производная х по времени, а сама связь линейна, то это линейное дифференциальное уравнение. Пусть оно имеет, например, следующий вид:

где k — коэффициент. В этом уравнении kxe — свободный член; без него уравнение x=kx называется однородным и его общее решение х=сеkt. Исходное неоднородное уравнение имеет частное решение х = хe (если величина х находится в состоянии равновесия), а общее его решение есть сумма любого частного решения и общего решения однородного уравнения, т.е. х = Xe + сеkt.

Учитывая, что при t=0 величина х равна х(0), получаем с=х(0)-хe, x(t)= х+(х(о)- xe)ekt. Если k0, то еkt

0 и равновесие устойчиво, то есть при отклонении величины х(t) от значения хe она вновь стремится принять это значение.

При k 0 величина еkt —

и, соответственно, х(t) стремится к бесконечности (если начальное состояние не совпадает с состоянием равновесия).

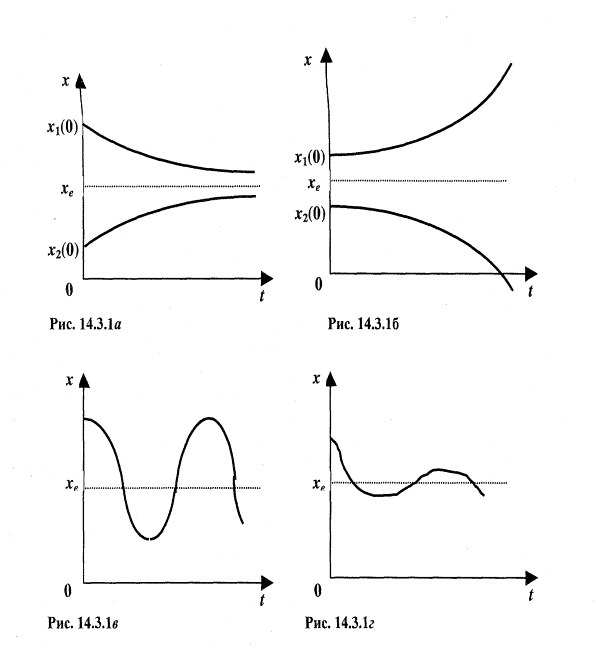
Система приходит к состоянию хe различными способами: как это показано на рисунке 14.3.1a.; на 14.3.1б (при к 0) или на 14.3.1в,г.

Поведение в дискретном времени может быть описано с помощью разностного уравнения, связывающего величины х в соседние моменты времени, то есть xt и хt-1.

Например, в дискретной ситуации, аналогичной уже описанной, может использоваться разностное уравнение хt = хt-1 + k(xt-1 – хe), решением которого является х = хe + (х(0)— Xe) (1 + r)t . Это решение может быть найдено (аналогично непрерывному случаю) как сумма общего решения xt = c(l + k)t для однородного уравнения xt=(l+k)xt-1 и частного решения xt = xe для исходного разностного уравнения; с учетом хt = х(о) при t = 0. При k 0 система в случае отклонения от xe будет двигаться в направлении xe, при k 0 уходить еще дальше от него. Равновесие устойчиво при -2 k 0 и неустойчиво при k 0 или k -2 (при k -1 показатель х каждый раз «перескакивает» равновесное значение х, причем при k -2 — слишком далеко, чтобы приблизиться в конце концов к х).1

Нужно отметить, что математическое моделирование предполагает определение элементов, составляющих модель, с целью их введения в конкретную модель экономического равновесия. Причем под экономическим равновесием понимается такое состояние системы, которое характеризуется равенством спроса и предложения всех ресурсов, где элементы модели должны совпадать с элементами экономического равновесия.

В целом, в рамках моделирования экономических систем рассматривается вопрос — насколько точно модель экономической динамики отражает процессы, реально происходящие в экономике. Достоверность отражения моделью реальных экономических процессов основывается на практической оценке сопоставления реальности и модели экономической динамики.

Существуют два вида моделей макроэкономической динамики, реализующих дискретный и непрерывный подходы. В обоих случаях модели носят весьма общий, абстрактный характер. В то же время решение может быть найдено в явном виде, причем из него вытекают важные особенности для различных частных случаев соотношения параметров. На этих моделях удобно продемонстрировать простейший аппарат дискретного и непрерывного динамического моделирования, проиллюстрировать важнейшие категории и проблемы макроэкономической динамики.

Содержание раздела