d9e5a92d

Свойства OLS оценки в конечных выборках

Qe2xx Л xixi(yi xiP) ^ Qe2x
П -‘г-'
1
i= 1
Итак, состоятельная оценка вариационной матрицы OLS оценки в случае гетероекедаетичноети запишется как:
3 Q-x Qe2xxQ2
^2xixi) (nУxixi(yi-УО2) (nуxixi
i=1 ) \n i=1 ) \n i=1
ч _1
1 П
Будем называть стандартной ошибкой параметра Д величину:
se[(3i) =
Тогда t-статистика будет пивотальной оценкой, асимптотическое распределение которой является стандартным нормальным:
N (0,1).
3 - fa d
se(/3j)
Вальдовекая статистика для ограничений общего вида h(P) = 0, где число ограничений l k, имеет распределение Хи-квадрат:
W = h(/3)' \H3в']-1 h(3) -+ x2(l).
Здесь использовано обозначение:
dh(e)
дв'
3 Свойства OLS оценки в конечных выборках
Выедем следующие обозначения:
X = (xi,x2,... ,хпУ; Y = (уі,?2,...,?пУ; е = (ei,e2,... ,en)'.
Тогда уже знакомую нам регрессионную модель линейного условного среднего можно переписать в матричном виде:
Y = Хв + е; E [e|X ] = 0.
Оценка OLS в таком случае запишется как
Д = (X' X )-1Х 'Y = в + (X 'X )-1Х 'е.
Эта оценка обладает следующими свойствами:
- Условная несмещенность:
E[e|X ] = в + (X 'X )-1X'E [e|X ] = в.
- Безусловная несмещенность (следуют из условной несмещенности),
- Условная вариация оценки:
Var[f3lX] = (X'X )-1X'QX (X'X )-1, где Q = Var[Y|X] = E[ee'|X].
4 Оценка по обобщеному методу наименьших квадратов (GLS)
Определение 1 (класс линейных оценок): Пусть E[Y|X] = Xв¦ Классом линейных оценок в называется класс, содержащий оценки вида A(X)Y, где A(X) -матрица k х и, которая зависит только от X,
Пример: Для OLS оценки: A(X) = (X'X)-1X'.
Определение 2 (класс линейных несмещенных оценок):
Пусть E[Y|X] = X^, Классом линейных несмещенных оценок в называется класс, содержащий оценки вида A(X)Y, где A(X) - матрица k х и, зависящая только от X и удовлетворяющая условию A(X)X = Ik.
Пример: Для OLS оценки: A(X)X = (X'X)-1 X'X = Ik.
Заметим, что Var[A(X)Y|X] = A(X)QA(X)', Мы хотим найти наилучшую линейную несмещенную оценку, которая минимизирует Var[A(X)Y |X],
Теорема (Гаусса-Маркова): Наилучшей линейной несмещенной оценкой (BLUE) линейной регрессии условного среднего является оценка:
3 = A*(X )Y;
A*(X) = (X'Q-1X )-1X'Q-1.
В этом случае вариационная матрица оценки имеет вид:
?агЩХ] = (X'Q-1X )-1.
Доказательство: Очевидно, что оценка 3 принадлежит классу линейных несмещенных оценок:
A*(X )X = Ik.
Возьмем произвольную матрицу A(X), такую, что A(X)X = Ik, В этом случае имеют место следующие равенства:
(A(X) - A*(X))X = 0;
(A(X) - A*(X))QA*(X)' = (A(X) - A*(X))QQ-1X(X'Q-1X)-1 = 0.
Тогда:
Var[A(X )Y |X] = A(X )QA(X)' =
= (A(X) - A*(X) + A*(X))Q(A(X) - A*(X) + A*(X)) =
= (A(X) - A*(X))Q(A(X) - A*(X))' + Var[A*(X)Y|X] Var[3|X].
Следовательно, оценка /3 является наилучшей в классе линейных несмещенных оценок, Именно эта оценка и называется оценокой обобщенного метода наименьших квадратов (GLS),
Следствие 1: Оценка GLS /3 является эффективной в классе линейных несмещенных оценок.
Следствие 2: Если ошибка линейной регрессии условного среднего обладает свойством условной гомоекедаетичноети, то (3gls = Pols- Т.е. OLS и GLS оценки совпадают.
Ниже приведена таблица, содержащая условные вариационные матрицы оценок OLS и GLS в конечных выборках для случаев гетеро и гомоекедаетичноети:

OLS GLS
Гомоекедаетичноеть a2(X 'X )-1 a2(X 'X )-1
Гетероекедаетичноеть (X 'X )-1X 'QX (X 'X )-1 (X 'Q-1X )-1

Замечание 1: Оценка GLS 3 является недоступной, поскольку матрица О неизвестна.
Замечание 2: Оценка GLS в является частным случаем оценки взвешенного метода наименьших квадратов WLS:
3wls = (X 'WX )~lX'WY, где W - положительно определенная матрица.
5 Асимтотические свойства оценок GLS
Рассмотрим асимтотические свойства GLS оценки. Для этого представим ее в следующем виде:
n , \ -1 1 n
XjXj \ ^ xiei
п a2(xi)J п a2(xi)'
Пользуясь законом больших чисел и центральной предельной теоремой, получим:
р . Гр'
ХДЦ' i
a2(xi)
xiei
a2(xi)
xiei
a2(xi)
0;
iW
XieПоследнее выражение следует из того, что:
E [e2lxi]
Q щ.
a2
Таким образом, оценка GLS является состоятельной и аеимтотичееки нормальной. Ниже приведена таблица, содержащая асимтотические вариационные матрицы оценок OLS и GLS для случаев гетеро и гомоскедастичности:

OLS GLS
Гомоскедастичность 2Q-X Q = 0’"2QXx1
Гетероскедастичность Qxx Qe2xxQ-x q-1
Q XX
__

Теорема: Оценка GLS в асимптотически эффективна в классе оценок вида:
-і
"У ZiU
п
вIV
ZiX'i
i= 1
i= 1
где zi = f (xi) для любой функции f : Rk ^ Rk.
Доказательство: Заметим, что оценки OLS и GLS принадлежат указанному классу,
т.к. для OLS zi = xi; а для GLS zi =
. Рассмотрим оценку
-2(xi)
-і
1Е ZiXi 1Е Ziyi.
1 ' I 1 '
Рту
i=1
i=1
Легко показать, что она состоятельна и асимптотически нормальна, Аеимтотичеекая вариационная матрица этой оценки выглядит следующим образом:
Vzz Q-x Qe2zzQxz ,
ГДе Qzx E[zixi]j Qe2zz
вариация оценки GLS равна Q
E[zizie2] = E[zizia2(xi)]. Зная, что асимптотическая
Л1, рассмотрим разность:
^2
-1
xixi
Vzz - QxX = (E[Zixi]) 1 E[Zizia2(xi)] (E[xizi]) 1 - ( E
,-i
a2(xi)
/141
(E [viui]) 1 E[vivi](E [uivi]) 1 - (E [uiui])
,/14-1
/14 1
./14 1
(E [viui]) 1 E [vivi] - E [viui] (E [щиД 1 E [u^i] (E [uivi])
/14 1
(E[viui]) 1 E[wiW] (E[uivi]) 1 0.
Здесь vi = zia(xi); ui = -X-G; wi = vi - E[viui](E[uiui]) 1ui. Таким образом, мы
-(xi )
показали, что оценка GLS асимптотически эффективна.
Результат: Оценка GLS является аналоговой оценкой, полученной по принципу аналогий. А именно, оценка GLS получается из условия:
1 ~ Е(Уі - xi/3) x
xi
0.
0;
ei
a(xi)
i=1
a(xi)
Отсюда получается оценка GLS (3.
6 Доступная оценка GLS
Как уже было замечено, для того, чтобы получить оценку GLS нам необходимо знать вариационную матрицу ошибок Q (или a2(xi)). Естественно полагать, что эти параметры являются неизвестными априори, поэтому они должны быть оценены.
Обычно в таких случаях предполагают, что дисперсия ошибок сеть линейная функция от некоторой трансформации xi:
a2(xi) = E [e2|xi] = zi у,
где Zj есть некоторая трансформация xi; например zi = xi или zi = x?, Если предпо
ложение правильное, то можно построить регрессию на остатках, а именно:
e = zjY + ?і; E [e|zj] = 0.
Затем, оценив исходную регрессию и регрессию на остатках, имеем:
7j = Уі - х'іІЗ = ej + x-(в - в);
Y.
ziz'j zie? + ? zix'(в - 7)ei + ? zi(x'(в - 7))^
Таким образом, мы получаем состоятельную оценку дисперсии ошибки:
7?(хі) = zi 7
после чего, мы можем построить доступную оценку обобщенного метода наименьших квадратов (FGLS):
-і
xiyi
i=1 2(хі) ) 72(хі)
(X 'П-1X )-1X 'П-1Y.
Pf
Приведем алгоритм построения оценки FGLS:
1, Используя метод OLS оценить исходную регрессию и получить остатки 7І для i = 1,..., п Прогнать регрессию на остатках, получить оценки 7 и построить оценки дисперсии ошибок 7 (xi) или П,
-1
rp . /V*'
A'jvt'i
7 (Xj)
xiyi
Pf
(X '7-1X )-1X '7-1Y.
72(xj)
Вообще говоря, такой алгоритм построения оценок дисперсии ошибок не гарантирует их положительность. Ниже приведены способы как избежать 7 (xi) 0,
1, Выбрать некоторое 6 0, Затем, положить:
7(xi) = max(zj7; 6).
2, Выбросить наблюдения, для которых 7(xi) 0,
3, Положить 72(хі) = П Y^j=1 zj7 для тех наблюдений, для которых 7(xi) 0,
Результат: Если екедаетичная функция (зависимость условной дисперсии ошибок от я*) правильно определена, то оценка доступного метода GLS Др асимптотически эквивалентна оценке GLS /3. Т.е.:
?П(/Зе - в) N(0,Q-X).
О2
Состоятельная оценка асимптотической вариации в этом случае равна:
,x %Xi a2(xi)
Если екедаетичная функция определена неправильно, то оценка Др, тем не менее, остается состоятельной и асимптотически нормальной:
ДП(/Зр Д) ^ N (о, QJQг*e2Q
где использованы следующие обозначения:
/V* . /V*'
j^ij^ * 2
/у . /у-i
Q x2 = E
a2
Q xx e2 E
Lz^r L(ziY)2
Состоятельная оценка асимптотической вариации в этом случае равна:
-i
-1
/у* . /у7 f /у . /у7
(Ж2 43
X*Xj
; Zi 7
\ Л Xi
7v
7 Регрессия с неслучайной выборкой
В случае, когда наблюдения представляют собой неслучайную выборку, вариационная матрица ошибок Q Var\Y\X] не является диагональной. Вариация OLS оценки 3 (X'X)-1X7Y в этом случае:
Var[/3\X ] (X'X )-1X'QX (X'X )-1.
Вариация GLS оценки Д (X'tt-1X)-1X'tt-1Y:
Var[/3\X ] (X'Q-1X )-1.
Таким образом, чтобы построить пивотальную статистику в случае неслучайных наблюдений необходимо параметризовать вариационную матрицу ошибок Q небольшим числом параметров.
8 OLS и GLS во временных рядах
Рассмотрим следующую регрессионную модель:
yt = х'Ф + et; E [et|/t-i] = 0; E[e2 = a2(It_i),
где {(xt,yt)}T=1 - стационарный и эргодичный процесс, а
It_1 {yt_ 1, yt_2 , . . . ; xt, xt_1 , . . . }
Примерами таких моделей могут служить следующие:
- AR(p) - процесс, когда xt = (yt_i,yt_2,... ,yt_p)/-
- Модель формирования обменного курса валют:
st+i st = а + P(ft st) + et; E [et1 It_i] = .
Здесь ft - цена форвардного контракта, a st - текущий обменный курс,
- Модель формирования инфляции:
nt+1 = а + Pit + et; E [et|It_i] = .
Здесь nt+1 - инфляция, a it - процентная ставка.
Заметим, что условное математическое ожидание на X E[Y|Х] = Хр.
Рассмотрим свойства оценок OLS и GLS в указанной выше модели,
OLS оценка: Ясно, что оценка OLS состоятельна:
(т \ -1 т
xtxt) xtyt-^ ^.
t=i j t=i
Это следует из того, что:
E [xtet] = E [E [xtet|It_i]] = E [xtE [et|It_i]] = 0.
Кроме того, из центральной предельной теоремы для последовательности мартин-гальных приращений следует асимптотическая нормальность OLS оценки:
СГ(Д - в) -- N(0, Ve); Ve = ,
где Qxx = E [xtxt]; Qe2xx = E \xtx'te^\. Недиагональные элементы матрицы Qe2xx равны 0, поскольку:
E [xtetx't-j et-j ] = E [E [xtetxt- et-j |1t-i]] = E [xtE [et| It-i]xt-j et-j ] = 0.
GLS оценка: Оценка GLS в моделях с отсутствующей серийной корреляцией ошибок, очевидно, тоже будет состоятельна и асимптотически нормальна. Выглядит GLS оценка следующим обрзом:
-1 T
xt
^2(1t-1)
xt
2(It-1)
yt.
xy-
На практике GLS оценка редко используется во временных рядах, поскольку требует знания или состоятельного оценивания екедаетичной функции a2(It-1), которая потенциально зависит от всей предыстории.
Теперь рассмотрим общую регрессионную модель временных рядов с серийной корреляцией ошибок:
yt = xtP + et; E [et|1t-q] = 0; E [e2|1t-q] = V2(It-q), где It-q = {yt-q ,yt-q-1, . . . '; xt,xt-1, . . .}.


Примерами таких моделей могут служить следующие:
- Модель ARMA(p, q)\ xt = (yt-q, yt-q-1,..., yt-q-p+1)'-
- Модель формирования обменного курса валют:
st+q st = а + в (ft;q st) + et; E [et|It-q] = 0.
Здесь ft;q - цена форвардного контр акта на q периодов вперед, a st - текущий обменный курс,
- Модель формирования инфляции:
nt+q = а + eit;q + et; E [et|It-q] = 0.
Здесь nt+q - инфляция, a it;q - процентная ставка на q периодов вперед.
Оценка остается состоятельной и асимптотически нормальной, т.е.:
?Т(Д- в) N(0, Ve); Ve = Q-JfexQ
e2xx
где матрица Qe2xx считается по формуле:
OLS оценка:

1

Д = ]xtyt.
xx
Qe2xx E [xtx't ef] + ^(E[xt xt-j etet-j ] + E [xtxt+j etet+j ]).
Для j q 1:
E [xtx't-j etet-j ] = E[E [xtX't-j etet-j |1t-q ]] = E [xtxt-j E [et|/t-]et-j ] = 0.
Чтобы состоятельно оценить асимптотическую вариацию оценки OLS Vp в случае серийной корреляции ошибок нужно пользоваться формулой Ньюи-Веста.
GLS оценка: Оценка GLS не используется в моделях е серийной корреляцией ошибок, Заметим,что в этом случае:
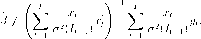V Линейные модели е инструментальными перемен
ными
1 Эндогенные переменные
Бывают случаи, когда условное среднее на независимой переменной на регрессорах E[y|x] не является интересующим нас объектом. Приведем несколько примеров:
Пример 1: Пусть E[y|x*] = (x*)'^, однако переменные x* являются ненаблюдаемыми, Вместо этого, исследователь наблюдает переменные x = x* + и, где и - независима от x* и у, В этом случае, как легко показать, регрессионная оценка OLS будет несостоятельной:
у = (x*)'^ + e = (x и)'в + e;
у = x'P + v; v = e u' в; E [xv] = E [(x* + u)(e и' в)] = E [uu'] = 0;
E[v|x] = 0 ^ Д -?- Д
В такой ситуации мы имеем смещенность оценки, связанную с ошибкой измерения.
Пример 2: Пусть у нас есть система линейных уравнений:
Спрос: Q = ві P + ep
Предложение : Q = в2 P + e2;
где ( ) ~ iid(0, I2).
?е2/
Очевидно, что в этом случае регрессоры коррелируют с ошибками, т,е,:
E [ei|P]=0; E[e2|P] = 0.
Тогда, используя оценку OLS в регрессии Q на P, получим:
p E [QP]
E [P2]
Решая исходную систему легко получить:
Q\ = 1 (в2 ві \ /еі
p) = ві+Ж\ 1 -J Ve2
Откуда сразу же следует:
e [QP] = I27г; E [P2]
ві + в2 в1 + в2
Таким образом, оценка OLS несостоятельна ни для въ ни для в2;
ъ E [QP] = в2 - ві в ' E [P2] 2 .
В обоих примерах переменные, коррелирующие с ошибками, являются эндогеными.
Определение: Переменная x эндогенной в структурном уравнении у =
х'в + e если E[e|x] = 0,
Определение: Вектор z размерности l называется инструментом для регрессионного уравнения у = х'в + e если E[e|z] = 0, т,е, z - экзогенная переменная.
Заметим, что в обычной регрессии условного среднего регрессоры являются экзогенными переменными, Т.е. для модели:
у = х'в + e; E [e|x] = 0; E [e2|x] = а2(х),
z = x является инструментом и экзогенной переменной.
2 Случай, когда количество инструментов и регрессоров совпадает
Рассмотрим случай, когда количество инструментов l совпадает с количеством регрессоров к, т.е. l = к, Пусть матрица Qzz = E[zz'\ невырождена. Из определения инструментов следует:
E [e|z\ = 0 ^ E [ze\ = 0.
Последнее условие носит название условия валидности инструментов, Применяя к нему принцип аналогий, получим условие:
1 п
- V\zi(yi - x'ifiiv) = 0.
i= 1
Из этого условия, получаем инструментальную оценку:
(п \ 1 п
5i Е*у-
i=1 ) i= 1
Заметим, что для того, чтобы получить инструментальную оценку необходимо выполнение условия релевантности, т.е, матрица E[zx'\ должна быть невырожденной, В матричном виде инструментальная оценка выглядит следующим образом:
ві? = (Z'X )-1Z'Y; Z = (z1 ,z2,..., zn)'.
В конечных выборках инструментальная оценка смещена, однако является состоятельной и асимптотически нормальной:
E [в/v |Z,X \ = (Z X )-1Z' E [Y |Z,X \ = в;
кП(в/? - в) ± N(0, Ve); Ve = Q1Qe2zzQ-z1.
Состоятельные оценки матриц Qzx,Qe2zz:
ді yi хівІ?.
ziz'e2-
Qe
р.
л.
1 n
Qzx =1У
i=1
Замечание: Домножение инструментальных переменных на любую соразмерную невырожденную матрицу констант C те меняет вида инструментальной оценки /3І?.
3 Случай, когда количество инструментов превышает количество регрессоров
Рассмотрим случай, когда l к, Пусть матрица E[ziz'i\ = Qzz невырождена. Идея построения инструментальной оценки в этом случае состоит в том, чтобы найти линейный предиктор x с помощью z:
Xi = Г zi + Ui; E [ziu'i ] = 0. Из последнего условия находим Г:
E[zi(xi - rzi)'] = 0;
^ Г' = (E [zizi ])-1E [zixi] = Q-^Qzx
Теперь, возвращаясь к исходной структурной форме можем переписать:
Уі = xie + ei; E [ei|zi] = 0;
^ Уі = (rzi + Ui)'e + ei = (rzi)'e + ?і; Vi = ei + uifi. Очевидно, выполняются следующие соотношения:
E [Г ziVi] = rE [zi(ei + ui/)] = 0.
Тогда, параметр структурной регрессии можно записать:
в = (E [ГZi(ГZi),])-1E ГіУі] = (Qxz Q-z1Qzx)-1Qxz Q-^Qzy.
Применяя принцип аналогий получим инструментальную оценку для случая, когда число инструментов превышает число регрессоров:
-1
-1
-1
n /и \ n \ n /и \ n
^2SLS = (5^ xizi (5^ zizi I zixi ) xizi ( X] zizi ) S ziyi.
i=1 \i=1 / i=1 ) i=1 \i=1 / i=1
Или в матричной форме:
e2sLS = (X'Z (Z'Z)Z'X )-1X'Z (Z'Z)Z'Y.
Эта инструментальная оценка состоятельна и асимптотически нормальна, однако не является эффективной в общем случае.
E [ziei] = 0 ^ /?2sls ^ в; Vn(/^2SLs в) ^ N(0, V2sls);
Особым случаем является случай условной гомоекедаетичноети, когда E [e?|zj] = а2 = const. В этом случае асимптотическая вариационная матрица упрощается:
-1
V2SLS а (QxzQzz Qzx)
поскольку Qe2zz = a2Qzz,
Заметим, что для того, чтобы построить оценку (32SLS, необходимо выполнение условия идентификации, т.е. ранг матрицы Qxzдoлжeн быть равен количеству регрессоров k:
rank(Qxz) = k.
Замечание: Оценку j32SLS можно выразить следующим образом:
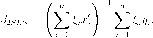
Здесь - инструменты, С точки зрения эффективности полученной оценки инструменты являются неоптимальными,
4 Случай, когда количество инструментов меньше числа ре-гессоров
Если матрица Qzx имеет ранг, меныний k, то условие идентификации не выполнено, В этом случае, построенные инструментальные оценки будут иметь другие (плохие) асимптотические свойства.
Пример: Рассмотрим следующую модель:
l = k = 1; yi = вхі + вц, E [eilzi ] = 0; E [xiZi] = 0.
Последнее выражение означает, что не выполнено условие релевантности инструментов, Согласно центральной предельной теореме выполняются следующие соотношения:

Qz2x2 ) .

Таким образом, инструментальная оценка уже не будет асимптотически нормальной:
ві? = |^ = в + /П ^ ^ 4 в + Cauchy. zixi ,/n,z2i ZiXi
Т.е.. асимптотическое распределение оценки не является асимптотически нормальным и не имеет среднего.
Если у нас есть подозрение, что инструменты нерелевантные, стоит вначале протестировать гипотезу: H0 : E\xizi] = 0, Если гипотеза отвергается, то инструмент релевантный.
5 Бутстрапирование оценок инструментальных переменных
Процедура бутстрапа для инструментальных оценок практически ничем не отличается от построения бутетраповекого распределения для обычной статистики независимых наблюдений. Из исходной выборки (xi, yi, zi) строится псе вдовы борка {(x*, y*, z*) }п=1.
Случай l = k (Just ID):
Ді? = (У zixi) 52 ziyi;
-i
-i
в!? = (У z*xi*) 52z*yl;
Асимптотическая вариационная матрица:
-i
еі? = п (у zixf) у ziz'е2 (у xizi
Её бутстраповский аналог:
е? = п (у z* xi*)- у z* 4*е2 (у x* z
Случай l k (Over ID): Сразу заметим, что хотя в популяции выполнено условие E\ziei] = 0, для эмпирической функции распределения оно нарушается, т.е,
1 п
Л ziei = 0.
п -‘Н'
Таким образом, делая бутстрап, не нужно забывать про рецентрирование. Итак, инструментальные оценки:
-1
%sls = (...) 1 уxizi(52ziz0 52ziyi;
(.. .*)-1 у x*zi * (у z*zi *) 1 (у z*y* - у,
2 SLS
Асимптотические вариационные матрицы:
e2SLS = п(...) 1 ^ Xiz'i ZiZ') ^ Ziz'ef Ziz') ^ ZiXi(...) 1;
-і
= n(.. . *)1 ^ x*z'* z*z'*^ 1 ^ u*ui* z*z'*^ 1 ^ Z*X*(.. .*)
Здесь и* = Z*е* - П ЦЦ Zjej.
6 Инструментальные переменные во временных рядах
Рассмотрим следующую модель временного ряда:
yt = х[в + et\ E [et\It-i ] = 0;
It 1 {yt- 1, yt-2 ... ; Xt, Xt- 1 , . . . } ;
Zt (yt1, yt2 , . . . , yt ly ; xt, Xt 1, ... , Xtlx ) .
Результат: Оценка (32SLS состоятельна и асимптотически нормальна:
в2SLS ^ в; ?Т(в2SLS в) ^ N(0, V2sls).
Инструментальная оценка j32SLS является асимптотически более эффективной, чем оценка OLS,
Теперь рассмотрим модель, допускающую автокорреляцию ошибок:
yt = XtP + et; E[et\Itq ] = 0; Zt = {ytq ,...,ytiy; Xt,...,Xtix}'.
Хотя общие результаты здесь такие-же, как и в предыдущем случае, для вычисления асимптотической вариации необходимо использовать формулу Ньюи-Веста из-за серийной корреляции ошибок.
VI Оценка регрессионных моделей с нелинейным средним
1 Нелинейности в регрессиях
Пусть условное среднее E[y\X] = q(x,P), где g(- , - ) - нелинейная функция, В этом случае мы имеем дело с нелинейной моделью. Тем не менее, существуют случаи нелинейностей в регрессиях, сводящиеся к линейному случаю с помощью трансформаций :
1, Пусть д(х,в) нелинейна то регрессорам x и линейна то параметрам в-, тогда можно выполнить такую трансформацию х ^ z, что E[y|z] = z'в-
Пример 1: Пусть условное среднее выражается нелинейной функцией регрессоров следующего вида:
д(х, в) = во + віХі + в2Х2 + взХіХ2 + в4Х? + вбХ^
Тогда подходящей трансформацией будет:
z = {1,Х1,Х2,Х1Х2,Х2, х2}.
Пример 2: Условное среднее выражается нелинейной функцией регрессоров следующего вида:
д(Х, в) = во + віХ + в2Х2 +----+ врХр.
Соответствующая трансформация регрессоров:
z = {1, Х,..., ХР}.
Тут, однако, необходимо отметить, что возникает сложность в интерпретации коэффициентов:
^ = ві + 2в2Х + - - - + рвРХр-1.
Неясно, какое х подставлять в данную формулу, чтобы получить численное значение. Варианты:
- Оценить в каком-то конкретном х, которое определяется из контекста задачи,
- Использовать среднее значение Х,
- Использовать средние значения степеней Х, х2,... ,хр-і
В любом случае, коэффициенты вь в2,..., вР не имеют экономического смысла. Имеет смысл только их некоторая комбинация,
2, "По-существу линейные" модели Рассмотрим такой пример:
уг = А%К*L- exp(ei); E[ег|А, К, L] = 0.
В данном примере логарифмическая трансформация модели сводит ее к линейному случаю:
E[log Y| log Аг, log Кг, log Li] = log Аг + a log Кг + (1 - a) log Li.
2 Нелинейные регрессионные модели
В данном разделе рассмотрим существенно нелинейные модели, которые не приводятся к линейным, т.е.:
E [y\x\ = д(хв) = z'e
для любой функции z{x).
Примеры:
- д(х,в) = A + А^ту;
- д(х,в) = ві + в2евзх;
- g(x, в) = (ві + в2Хі)1[х2 вз\ + (в4 + вбХі)1[х2 вз\.
Пусть функция д(х,в) дифференцируема по обоим аргументам.
Определение: Величина дя(в’в = дв(х,в) называется псевдорегрессором.
Пример: В качестве примера рассмотрим обычную линейную регрессию, т.е,:
д(х,в ) = х'в ^ дв (х) = х.
В данном примере пеевдорегреееор не зависит от параметра в-, однако, в общем случае, пеевдорегреееоры зависят от параметров модели,
3 Оценка нелинейного метода наименьших квадратов (NLLS)
Мы знаем, что параметр в есть решение минимизационной задачи:
в = argminE[(уі - д(хі,Ь))2\.
b
Используя принцип аналогий, получим оценку нелинейного метода наименьших квадратов (NLLS):
1 п
в = argmin- ?Чуі - д(х*, Ь))2. b n
i=1
Условие первого порядка:
1 п _
- У2(Уі - g(xi, в))дв(хі, в) = .
і= 1
Ясно, что точное аналитическое выражение для в получить в общем случае невозможно, поэтому обычно для построения NLLS оценок пользуются численными методами.
Получение оценки NLLS методом концентрации:
Одним из возможных численных методов получения NLLS оценки является метод концентрации. Разделим параметры задачи на две группы, удовлетворяющие условиям :
в = (y1 л2 );
д{х,в) = y1 x(Y2).
Т.е. грубо говоря, условное среднее линейно по параметрам и нелинейно по параметрам д2- Кроме того, предполагается, что число параметров y2 невелжо: к2 = 1 или к2 = 2,
Пример: В качестве примера приведем следующую модель:
д(х, в) = ві + в2евзХх.
Тогда соответствующее разделение параметров следующее:
Yi = (ві,в2)'-; Y2 = Аз ^ x(Y2) = (1,хевзж)/.
В подобных случаях используется 2-х шаговая процедура оценивания параметра:
min_5r(yi - Yixi(Y2))2
Y1 П ^
/3 = argmin
Y2
i=i
Поскольку размерность y2 маленькая, то оптимум легко находится на сетке.
Приведем алгоритм метода концентрации:
- Для параметра y2 на некотором интервале [y2, Y2] берется сетка,
- Для каждого y2 на этой оцениваетея 31(y2) методом OLS и вычисляется
численное целевое значение ^ YI(yi 31(y2)/xi(Y2))2-
- Из всех значений y2 на сетке выбирается то, для которого целевое значение наименьшее.
- Если необходимо, в окрестности полученного значения у2 строится более мелкая сетка, и процедура повторяется.
Получение оценки NLLS методом линеаризации:
Другим возможным численным методом получения NLLS оценки является линеаризация условия первого порядка. Допустим, что P1 - начальное предположение о численном значении оцениваемых параметров.Тогда, е помощью линеаризации предлагается итеративная процедура перехода Pj ^ Pj+1- Эта процедура продолжается до тех пор, пока для достаточно малого е не будет выполнено условие: \Pj+1 Pj| е. Более подробно, линеаризованное условие первого порядка для оценки NLLS:
1 п ^ _
- ^2(?і 9Іхг, Pj) 9в(xi, Pj)(Pj+1 Pj))gp(xi, Pj) ~ 0.
n i=i
Вводи обозначение;
(n \ 1 n
J^ge (xi,pj )ge (xi,pj )j J^ge (xi,pj )(Vi g(xi,/pj)),
i=1 J i= 1
получим итеративную процедуру в виде:
Pj+1 Pj + dj.
Если dj слишком велико (процедура те сходится), то выбир аетея некоторое A j ? [0,1], такое, чтобы целевая функция была минимальной, а процедура изменяется:
Pj+1 = Pj + Aj dj.
4 Асимптотические свойства оценки NLLS
Определение: Говорят, что задача удовлетворяет условию идентификации, если b = Д тогда и только тогда, когда g(x,P) = g(x,b) с вероятностью 1,
Можно переписать оптимизационную адачу нахождения параметра в этом случае как:
Р = argminЕ[(y g(x,b))2] = argmin [Е[(y g(x,p))2] + Е[(g(x,e) g(x,b))2]\ .
b b
Примеры:
- Рассмотрим в качестве примера идентификации линейный случай. Пусть матрица Qxx = E [хх'] - невырождена, Тогда, если в = Ъ выполняется соотношение:
E[(х'в - х'Ъ)2] = (в - b)'QxxX0 - b) 0.
Следовательно, х'в = х'Ъ.
- Рассмотрим теперь пример, где нет идентификации:
д(х, в) = ві + в2eв4+взx = ві + eloge2+e4+e3x.
Очевидно, что идентифицировать параметры в2 и в4 одновременно невозможно.
Определение: Последовательность случайных функций |^(0)}™=1 удовлетворяет равномерному закону больших чисел (РЗБЧ), если:
.. 1 sup У ? n
n ^ n
V Zi(9) - plim n V Zi(e)\\
0.
Лемма: Если последовательность (Zi(0)}rn=1 удовлетворяет РЗБЧ и 0 -X в, то: Доказательство: Запишем последовательность неравенств, воспользовавшись РЗБЧ и теоремой Манна-Вальда: ^ Zi(0n)
p lim Zi(0)
n
i= 1
i=1 -I ?,
plim Zi(0)
n ^
plim У^ Zi(0)
n ^
i= 1
i= 1
л n л n
sup
?
- V Zi(B) - p lim- V Zi(0) n ^ n
i=1 i=1
plim У^ Zi(0) n
plim У^ Zi(0) n
0.
i=1 -I ?.
i=1
Следствия: Следствиями доказанной леммы являются:
?
i= 1
(Зв
Qe2x
i=1
Qgg n ? ? дв(хі’Д)дв(хі’Д) * Qgg,
W Qgg = E\9l3(х,в)#в(х,в)/].
Теорема: Пусть выполнены следующие требования:
1, Выполнено условие идентификации: д(х,в) = д(х,Ь) при Ь = в-
2, Функция д(х, в) дважды непрерывно дифференцируема по Ь,
3, Для следующих последовательностей выполняется РЗБЧ:
(Уі - д(хив))2; де(х^в)дв(xi,в)/; (Уі - g(xi,в)) ддвдв*’в)
4, Матрица Qgg невырождена:
Qgg = E \дв(х,в )дв(х,в),].
5, Существует матрица:
Qe2gg E\дв(х’в)дв(х, в) e ].
Тогда для оценки NLLS выполнены следующие соотношения:
Д в; ^n(/p - в) N(0’ Q-glQe2ggQ-g1).
Доказательство:
1, Состоятельность: Для любого е 0 с вероятностью, стремящейся к 1 при n ^ то, мы имеем:
Х](Уі - д(хі’Д))
^2(Уі - д(хі’в))2 +
і= 1
i=1
т.к. оценка в минимизирует выражение:
1 п
-?^(Уі - д(хі’Ь))2. n
Поскольку РЗБЧ выполняется для (у д(хі,в))2, то:
Е[(Уі g(xi, Д))2] - ^2(Уі g(xi, Д))2 +е.
n 3
П
і=1
Аналогично:
- ХДуі g(xi, в ))2 Е [(Уі g(xi, в ))2] + q.
n ^ 3
і=1
Суммируя эти три неравенства, получаем:
E[(У gfe Д))2] Е[(У g(xi, в))2] + е
Теперь определим е, Для этого выберем открытую окрестность в N (в). Поскольку в решает задачу минимизации, то должно быть выполнено следующее соотношение:
, mf Е[(У g(x,b))2] Е[(У g(x,e))].
beN (в)с
Тогда выберем следующее е:
е = inf. Е[(У g(x,b))2] Е[(У g(x,e))].
beN (в)с
Соответственно, выполнено следующее соотношение:
Е[(У g(x,^)2] inf Е[(У g(x,b))2L
beN (в)с
что собственно означает, что в ? N (в). Следовател ьно, в в-
2, Асимптотическая нормальность: Разложим условие первого порядка в ряд Тэйлора вокруг в:
Е(Уі g(xi,в))gв (хі,в) +
і=1
n
(Уі g^^)) ^вдХ^ ^ ge (хі,в)/
+
n -‘Н'
(в в) = о,
і=1
где в лежит между в и в покомпонентно. Следовательно:
-1
(Уі g(xi,^)) ^ ge fo^ge (хі,^)/
і=1
n
-р УД(Уі g(xi, в ))ge (хі,в) vn ^
? і=1
32 = argmin
Y2
n Е(Уі- 3і xi (Y2))
і=і
(Уі g(xi,в)) в ^ ge(х’в (х'в
-1
N (0, Qe2gg)
Рассмотрим специальный случай:
E [е2| Xj\ = а2 = const.
В этом случае асимптотическая дисперсионная матрица имеет упрощенную форму: Qe^gg = ^Qgg ] ^ VniP - /3) Д N (0,
5 Эффективность и взвешенная оценка NLLS
Как уже говорилось, оценка NLLS является аналоговой оценкой, полученной из условия: E[еде(х,в)] = 0, Оказывается, можно построить другую аналоговую оценку несколько изменив условие:
фв(х,в) ' а2(х)
0.
Из принципа аналогий, соответственно:
П
J2(yi- д(х^,й)
i=1
дв (хг,/з)
а2(хі)
0.
Оценка в, полученная из этого условия является взвешенной нелинейной оценкой метода наименьших квадратов. Эта оценка является решением минимизационной задачи:
в = argmin b n
i=1
(yi- д(хі,ь)) а2(хі) '
Оценка WNLLS 3 состоятельна и асимптотически нормальна:
3 Д в; ?П(Р - в) Д N(0, Q-1);
а2
Q щ
а2
дв(х,в )дв(х,в У
а2 (х)
Результат: Оценка WNLLS 3 является асимптотически эффективной в классе оценок, удовлетворяющих условию:
1 п
-У](Уі - g(xi, Piv ))zi = Ф
i=1
где zi - произвольная функция от хі; имеющая ту же размерность к х
6 Приложение: Модель бинарного выбора.
Рассмотрим следующую нелинейную модель:
1 x'iP + ei 0;
0 иначе;
ei|xi ~ N(0,1).
Уі
Тогда условное среднее:
E [уі|хі]
P{хів + ei 0|хі} = P{ei -хів|хі} = Ф(хІв).
Оценка NLLS в этом случае:
1 n
в = argmin у (yi Ф(x'b))2;
ь n U
в Л в; ?П((3 в) Л N(0, Q-gtQe*ggQ-);
Qgg = E [/ (хів )2xixi]; 9в (хі,в) = / (хів )хі;
Qe2gg = E [/ (xi в )2 (Уі Ф(хІв ))2xiXi].
Эффективная оценка WNLLS:
a2(xi) = ?йг[уі|хі] = Ф(хІв )(1 Ф(хІв)) = const;
Д - 1 ^ (Уі Ф(хІb))2
р = argmin у -
і. n
ь n 7=1 Ф(хІ/3)(1 Ф(ХД))
f (x' в)2хІх І
Ее асимптотические свойства:
Д Л в; ДД в) Л N (0, (E
-Ц
Ф(Х в )(1 ф(хІв))
7 Статистические выводы, когда при нулевой гипотезе один из параметров неидентифицирован.
Существует особая ситуация, когда тестирование статистических гипотез нестандартно, Рассмотрим два примера:
Пример 1:
1
1 + eXi - в
E [ei |хі] = 0.
(А + в2хі) + (в3 + в4хі)
+ ei;
Уі
Если нулевая гипотеза состоит в том, что в3 = в4 = 0, то при этой нулевой гипотезе параметр в5 не идентифицируется. Такая ситуация приводит к нестандартной процедуре построения теста.
Пример 2: Рассмотрим вариант ARCH-M модели:
yt Ра + х'Фі + + et; E 1 ^t 1] 0;
E [et2|/t1] at ao + ад2 r
Если нулевая гипотеза состоит в отсутствии ARCH эффекта, т.е. H0 : a1 0, то при нулевой гипотезе параметр 7 не идентифицируется.
Решение проблемы: Пусть в (в1 ,в2) где в1 идентифицируется при нулевой гипотезе, а в2 - нет. Постоим ВальдоБСкую статистику W(в2) для всех возможных значений в2. Тогда статистика:
sup W supW (в2)
в2
сходится по распределению к некоторому нестандартному распределению, которое получают с помощью симуляций.
63 В дальнейшем мы подробнее обсудим бутстраповский подход Здесь ns - скорость сходим ости; у - асимтотическое сме щение; ? - асимптотическая дисперсионная матрица. Эфроновский доверительный интервал: В данном случае, статистикой, используемой при бутстрапе, является интересующая нас статистика, т.е. ? = Д Таким образом, мы получаем бутстраповское распределение {?П = ДДД^ Соответствующие квантили распределения: Д/2, Д-а/2- Доверительный интервал:
СІЕ = \qa/2; ql-a/2].
Эфроновский доверительный интервал был популярен, когда бутстраповсий подход только начинал использоваться. На самом деле, этот доверительный интервал дает плохую аппроксимацию истинных уровней значимости, поскольку сохраняет смещение исходной выборки. Симметричный t-процентный доверительный интервал: Использует в качестве бутетрапируемой "симметричную t-статистику": |/3~~|, Соответствующее распределение б?тетраповекой статистики: \ 13-3 I . Квантиль: q^, До-
I se(P{, ) J ь=і
верительный интервал:
CI|t| = Ф 8еФ)оі-а; 3 + se{f3)q1_a\.
Симметричный t-процентный доверительный интервал имеет в определенных случаях преимущество перед t-процентным доверительным интервалом, А именно, если асимптотическое распределение статистики 3 в симметрично, то CI|t| дает лучшую аппроксимацию уровней значимости. n
¦E(x) = -V 1[xi x]; n ¦‘f^ Построение псевдовыборки по остаткам (специальный случай): Если исследователь знает, что ошибки и регрессоры независимы и, кроме того, ошибки распределены нормально, т.е. ei ~ N(0,а2), то эффективность бутстрапа Построение пеевдовыборки из неперекрывающихся блоков: В данном случае исходная выборка делится на некоторое количество неперекрывающихся блоков фиксированой длины. Длина блока также как и в предыдущем случае выбирается исследователем.

Пусть исходная выборка состоит из наблюдений {yt}}[=1. Тогда в первый блок войдут наблюдения y1,...,yl; во второй -yi+1,..., y2l; и наконец, в последний у-ый блок - наблюдения y[т]-l+1,..., y[т].

При построении пеевдовыборки блоки выбираются случайным образом с возвращением, длина пеевдовыборки совпадает, как правило, с длиной исходного ряда. Построение стационарной пеевдовыборки: Предыдущие два варианта построения пеевдовыборки, как правило, нарушают стационарность ряда, т.е, из Параметрическое оценивание: При таком подходе предполагается известным вид функции E[y\x\ = g(x, в), которая по предположению зависит от неизвестных параметров в €= Rk. Эти параметры оцениваются, что даёт оценку для g(x,e)¦ Таким образом, функция условного среднего параметризуется, отсюда и название метода.
Нужно отметить, что параметрический метод оценивания является более эффективным, чем непараметрический, если спецификация модели правильная, т.е. исследователь предположил правильный вид функции g(x,e)¦ Однако, если функция условного среднего параметризована неверно, то параметрическое оценивани приводит к несостоятельным результатам. Построить оценку FGLS: При фиксированном параметре y2 параметр y1 оценивается методом OLS: 3i(Y2) = (X/(Y2)X (Y2))-iX'(Y2)Y; X (Y2) = (xi(Y2),...,x2(Y2))/. Численно решается оптимизационная задача:



Содержание раздела