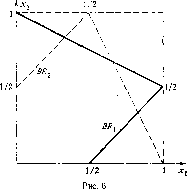d9e5a92d

ТЕОРЕМА НЭША О СУЩЕСТВОВАНИИ РАВНОВЕСИЙ

1) При (/, R) игрок 2 отклоняет кандидата d, а игрок 3 всегда выбирает правую дугу. Стратегия R есть доминирующая стратегия игрока 3, а ($, R)сложное равновесие. Выбирается кандидат а.
2) В (р1, L) и (ft, L) игрок 2 накладывает вето на с и а, в то время, как игрок 3 использует следующую стратегию L:
j идти направо, если игрок 2 накладывает вето на с или а, \ идти налево, если игрок 2 накладывает вето на d.
Стратегии наилучших ответов игрока 2 на L есть в точности {/, ft}. Более того, L это наилучший ответ как на /, так и на поскольку соответствует избранию наилучшего по иг кандидата d. Следовательно, (р, L) и (ft, L) NE-исходы.
Заметим, что L не только доминируемая (стратегией R) стратегия игрока 3, но также и рискованная (не осторожная) стратегия: применяя L, игрок 3 угрожает избрать с, если только игрок 2 отклонит d, но такой вариант крайне не выгоден обоим игрокам, поскольку снаихудший кандидат как по иг, так
Другой пример NE-исходов, использующих доминируемые стратегии, приведен в нашей простой модели аукциона: см. упражнение 2 ниже.
Заметим, однако, что когда все функции выигрыша взаимно однозначны на XN, то никакой МЕ-исхоя не содержит доминируемой стратегии и концепция равновесия по Нэшу обобщает равновесие в доминирующих стратегиях.
Упражнение 2
Для аукциона второго типа (пример 2 гл. I) докажите, что для каждого игрока і и любой цены р, ограниченной сверху ценностью товара для игрока і (р^а,-), существует Х?-исход, в котором і-й игрок получает товар за цену р.
Напротив, для аукциона первого типа покажите, что любой ХЯ-исход таков, что игрок 1 получает товар по цене между а2 и at.
Задача 1. Почти несущественная игра двух лиц
Пусть G = (Xj, Х2, и? и2)игра двух лиц, в которой Х± и Х2 конечны. Скажем, что G почти несущественна, если всем индивидуально рациональным исходам соответствует один и тот же вектор выигрышей. Другими словами, для любых двух исходов х и у выполнено
{х и у индивидуально рациональны} = {ыг (х) = и,- (у), і = 1, 2}.
1) Приведите пример почти несущественной игры, которая Не является несущественной.
2) Предположим, что игра G почти несущественна и выберем пару (xlt х2)^,Р1(и1)хР2(иг) осторожных стратегий. Покажите, что исход (Xj, х2) является оптимумом Парето, равновесием по Нэшу, t-равновесием по Штакельбергу для і = 1, 2.
3) Всякое ли равновесие по Нэшу в почти несущественной игре является также t-равновесием по Штакельбергу (і=1,2). А что получится, если обе функции выигрыша взаимно однозначны на X^XJ
2. ТЕОРЕМА НЭША О СУЩЕСТВОВАНИИ РАВНОВЕСИЙ
С теоретической точки зрения наиболее привлекательной чертой концепции равновесия по Нэшу являются его хорошие математические свойства.
Теорема Нэша дает достаточные условия существования по крайней мере одного равновесия по Нэшу. Эти условия оказались легко проверяемыми во многих прикладных моделях.
Уже отмечались два различных достаточных условия для того, чтобы игра G имела хотя бы один Х?-исход:
1) если игра G несущественна, тогда по теореме 1 гл. I любой набор осторожных стратегий есть равновесие по Нэшу.
2) если игра G разрешима по доминированию, тогда вступает в силу теорема 1 этой главы.
Однако удобных условий на X,- и иь гарантирующих несущественность или разрешимость по доминированию игры G, не существует. Для игры в нормальной форме обычной является ситуация, в которой и,- построены из элементарных функций (полиномиальных, логарифмических, ...) на основе элементарных операций.

В этом случае оказался весьма полезным результат Нэша.
Напомним, что действительная функция а вогнута, если для всех X, Ог^і^І, и любых t, t' выполнено
Ха (t) -f (1 X) а (t') *^a(Xt + (lX) f).
Теорема 2 (Нэш [1951]). Предположим, что для любого і ? N множество стратегий Х; есть выпуклое и компактное подмножество топологического векторного пространства (вообще говоря, своего для каждого і). Пусть для всех i?N и; непрерывная действительная функция на XN, определенная так, что для всех xi ? Xt функция ut (х;, xt) вогнута по х{ на Хг.

Тогда множество NE(G) равновесий по Нэшу игры G = (X,-, иг; i?N) непусто и компактно.
Доказательство. Доказательство опирается на теорему о неподвижной точке из выпуклого анализа.

Используем следующий результат, который известен как лемма Кнастера Кура-товскогоМазуркевича (ККМ), доказательство которой можно найти в работах: Берж [1957], Партхасаратхи, Рагхаван [1974].
Лемма. Пусть рцелое число и аи ..., арнекоторые точки топологического векторного пространства. П усть далее Ах, ..., Ар некоторые замкнутые подмножества множества СО {а,, ..., ар}, которое является выпуклой оболочкой множества {ах, ..., ар}, причем
?Гс:{1, ..., р} множество (J Ak содержит СО {ak\k^T}.
ks т
р
Тогда пересечение П Ak не пусто
*=і
Следующее короткое доказательство теоремы 2 принадлежит Жоржу Хаддаду.
Определим действительную функцию ф на XNxXNi Ф(х, 0)= 2 [/(*/. Удиі(У)] ПРИ г/СХд,.
іе N
Из вогнутости по Х[ следует вогнутость Ф по х. К тому же Ф непрерывна по у. Определим многозначное отображение Е из XN в себя;
F (x) = {y€XN\4(x, //)0} для всех x?XN.
Поскольку Ф непрерывна по у, то F (х).компакт при всех х. Более того, х g F (х), поэтому F (х) не пустое множество. Фиксируем целое р и р элементов х1, ..., хр из Xn. Утверждается,
ХИ Р
что любая выпуклая комбинация х= 2j Кхк принадлежит U F (хк).
kz=l k-\
В противном случае имеем
??=1, ..., р 0 Ф(х*, х).
Следовательно, мы доказали, что СО {х1, .... хр} с U F (хк).
Поскольку это справедливо для любого р и любых х1, ..., хр,
Р
к= і
то по ККМ лемме П F (хк) не пусто. Так как непустые компактные множества (F(x))xexN таковы, что любое их .конечноесемейство имеет непустое пересечение, то и пересечение всехмножеств п F (х) также не пусто.

Для любого х* из этого xexNпересечения имеемух? XN ф(х, х*)0, что может быть переписано в виде
?і 6 N, ?х,- ? X i ui (xh x?) u- (x*) ^ 0.
Таким образом, П F{x) NE(G) и теорема 2 доказана. Щ xsXn
Следствие из теоремы Нэша (фон Нейман). Пусть Хи Х2 выпуклые компактные подмножества некоторых топологических векторных пространств, и пусть иг непрерывная действительная функция, определенная на XtxX2, причем
1) для всех х2 ? Х2 (Хр х3) вогнута по х,,
2) для всех х1?Х1 и1{х1, х2) выпукла по х2.
Тогда игра двух лиц с нулевой суммой (Хи Х2, иг) имеет по крайней мере одну седловую пару и, следовательно, цену.
Теорема Нэша позволяет утверждать, что множество NE (G) не пусто. Для того чтобы его вычислить, требуется решитьследующую систему уравнений (i?N):
Uj (х*) max ut (хг, xf). (5)
*і€ хі
Если u( вогнута no xf, то приведенная выше задача глобальной оптимизации эквивалентна локальной задаче (как мы знаем из выпуклого программирования). Например, если х{ внутренняя точка множества Х; и функция и,- дифференцируема по х;, то условия (5) эквивалентны условиям
^ (х*) = 0 для всех і ? N. (6)
Поскольку число независимых уравнений равно размерности XN, можно надеяться, что система (6) будет иметь конечное число изолированных решений. По этой же причине для игр гобшріо положения равновесные по Нэшу исходы не оптимальны по Парето (точный результат см.

Грот [1974]).
Проиллюстрируем метод вычисления, который мы описали в общих чертах, на некоторых примерах и задачах.
Пример 4. Олигополия с назначением выпуска
Пусть имеется п производителей с нулевыми затратами, которые регулируют предложение хи ..., х„ некоторого насыщаемого по потреблению товара. Производители поставляют свой товар на рынок.

Общее предложение равно х = хх-}-...
х„, а цена есть р (х), где рубывающая вогнутая функция на положительной полуоси:
Р (0)0, р' (у) 0, р (у) 0 для г/ 0. (7)
Эту ситуацию можно представить как следующую игру:
X,- = [0, +оо), иі(х)=хір(х), і = 1, ..., п.
Из наших условий на р получается, что функция ut вогнута по х,-. Поскольку X, не компактные множества, положим, У, = = [0, S], где S есть предложение, порождающее нулевую цену: p(s) = 0. Для усеченной игры (Y{, иг; і=1, ..., п) применима теорема Нэша, которая позволяет утверждать существование ХЕ-исхода х в усеченной игре.

На самом деле исход х есть равновесие по Нэшу в исходной игре. Действительно, гарантированный выигрыш каждого игрока в усеченной игре есть 0, поэтому по лемме 1
г (х) 0 и, (уі, х,) для y{€[S, +оо).
В силу вогнутости н дифференцируемости и. на множестве X
Л/S'-исход х удовлетворяет системе (6):
xtp'(x)+p(x) = 0.
Таким образом, наша игра имеет единственный Л/Я-исход на диагонали:


Упражнение 3. Пример 4 (продолжение).
Докажите, что общий выпуск пх при NE-исходе больше выпуска х*, максимизирующего общий доход хр (х).
Докажите, что любая стратегия х{, для которой х* х{, доминируете* стратегией х*. Является ли данная игра разрешимой по доминированию?
Рассмотрим дуополию, которая формализуется как игра двух лиц, в которой множество стратегий каждого игрока есть отрезок [0, 1/2]. Докажите, что функция м,- (х) = x-tp (х) вогнута по х{.

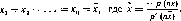
Вычислите функцию наилучших ответов обоих игроков и найдите Л/?-исход. Сравните его с границей Парето.
[1979])
Задача 2. Игра агентов по продаже автомобилей (Кейз
В игре участвуют п игроков, которые являются агентами по продаже автомобилей. Общий спрос фиксирован и равен D. Пусть х,-число автомобилей, которые агент і берет для продажи. Предполагая, что у каждого агента одно и то же число посетителей в единицу времени, получаем, что спрос на машины агента і равен


Пусть Р{доход агента с одного проданного автомобиля, а С{ его затраты на хранение одного автомобиля (в единицу времени). Тогда возникает следующая игра в нормальной форме!
1) Найдите недоминируемые стратегии игрока і. Является ли наша игра разрешимой по доминированию?
2) Докажите, что наша игра имеет два Л?Е-исхода и вычислите их. Являются ли они оптимальными по Парето исходами?
3) Сравните соответствующие Wi:-выигрыши в случае, когда
множество агентов разбито на подмножества (1..... nj,
{rtj + l, ..., п}, таких, что для всех і = 1, ...,.пг величина^
С- *
пренебрежимо мала, а для всех і = щ -f 1.....п величина
* І
положительная константа.
Задача 3. Финансирование общественных нужд по добро-вольной подписке
Предположим, что у каждого члена і сообщества N имеется некоторый запас денег М-г
Часть этих денег х) участник может выделить на общественные нужды. Его функция полезности vt (q, /п;) зависит от количества mt оставшихся у него денег, а также от суммы q денег, выделенных всеми участниками на общественные нужды.


Предположим, что функция v-t дифференцируема, строго монотонно возрастает по каждой переменной и вогнута по их совокупности. Таким образом, получается следующая игра в нормальной форме:

1) Докажите, что исход х оптимален по Парето в данной игре тогда и только тогда, когда он удовлетворяет уравнению ЛиндалаСамуэльсона:

2) Докажите, что функция и; вогнута по переменной xit и выведите существование NE-исхода. Охарактеризуйте NE-исход INI условиями первого порядка.
3) Докажите, что в любом ЛЧ?-исходе количество денег, выделяемых на общественные нужды, меньше оптимального уровня. Более точно, для NE-исхода существует доминирующий его по Парето исход, которому соответствует большее количество средств, выделенных на общественные нужды.
Задача 4. Игра двух лиц с нулевой суммой
Пусть Аь А2две положительно определенные рхр матрицы. Впроизвольная рхр матрица и, наконец, ait
Рассмотрим игру двух лиц с нулевой суммой (Xit Хг, щ), в которой
Xi=Xt = Rr,
^і(.^? *^2) = 2 Хі) + ВХЬ Х2У Ь ~2 {^2Х2 Х2У
+ 1. xt + a2, V-
Докажите, что эта игра имеет единственную седловую пару и вычислите ее.
Задача 5. Война на истощение (Милгром, Вебер [1980])
Каждый из двух игроков стремится завладеть некоторым предметом. Ценность этого предмета для игрока і описывается величиной V;. Победителем является тот, кто дольше остается агрессивным.

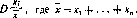
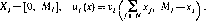
Предполагается, что затраты на агрессивность у обоих игроков одинаковы и равны единице. Стратегия х{ игрока і означает: Я буду агрессивным до момента времени t = x{, если только противник не остановится в некоторый момент времени х,- в последнем случае я остановлюсь в момент Лу + e для того, чтобы получить предмет с минимальными издержками.
1) Возникает следующая игра в нормальной форме:(при равенстве для определения победителя бросается монета). Докажите, что наша игра имеет в точности три оптимальных по Парето вектора выигрышей, два из которых соответствуют равновесиям по Нэшу (значит, есть борьба за лидерство).
Докажите, что в любом МЕ-исходе один из игроков использует свою единственную осторожную стратегию и получает гарантированный выигрыш, а другой очень рискованную стратегию.
2) Предположим, что ?і и ?2две независимые равномерно распределенные на [0, 1] случайные величины. Игрок і наблюдает ?{, но не наблюдает vf. Множество его стратегий теперь есть X,-:
Xj € Х(-: X; измеримое отображение из [0, 1] в Х{.
Функции выигрыша определяются так:
Щ fo. *) = $ и, (хг (oj), х2 (oj) dvt dv2.
[О, I]
Докажите существование в игре (Xj, Х2, иь и2) симметричного, доминируемого по Парето Х?-исхода х1 = х2 = х? и вычислите его. Заметьте, что при использовании игроками равновесных стратегий реализуются войны сколь угодно большой протяженности во времени.

Однако математическое ожидание длины войны конечно.
Указание. Предположите, что функция х* возрастающая и дифференцируемая. Докажите тогда, что для всех ?{ € [0, 1] функция
(**) 1 (у)Ф(у)= S (у,x*(t))dtу[\ (я*)-1 (у)]
одолжна достигать максимума на [0, + оо) при y = x*(vt).
3. УСТОЙЧИВЫЕ РАВНОВЕСИЯ
Даже в случае полной информированности (каждый игрок знает составляющие нормальной формы игры, включая функции выигрыша других игроков) концепция равновесия по Нэшу не может быть обоснована, исходя из рассмотрения изолированно принимаемых рациональных решений. Если допустим обмен информацией, то можно использовать сценарий с необязательным соглашением (см. разд. 1). Напротив, в процедурах нащупывания по Курно исследуется динамический процесс принятия близоруких решений, напоминающий механизм совершенной конкуренции.

Каждый игрок максимизирует свой выигрыш, полагая, что стратегии остальных игроков фиксированы. Эта процедура не может быть обоснована соображениями рациональности (поскольку предпосылка о том, что все остальные игроки будут неизменно использовать одну и ту же стратегию, постоянно нарушается).

Тем не менее процедура имеет определенную описательную силу и позволяет разделить /?Е-исходы на устойчивые и неустойчивые. Более того, ее реализация требует минимальной информированности игроков, которую мы будем называть полной неинформированностью (каждый игрок знает только свою собственную функцию выигрыша, а контакты игроков сводятся к совместному наблюдению стратегий)
Пример 5. Устойчивость в дуополии Курно с назначением вып усков
Два игрока поставляют на рынок некоторые количества xt и хг одного и того же товара, цена на который определяется следующим образом:
р(х)=\1с, где х = хг-{-х2.
Рассмотрим два различных предположения о функции затрат:
а) постоянные затраты на выпуск единицы продукции при увеличении масштабов производства: затраты на производство у единиц оцениваются величиной у для обоих игроков;
б) убывающие затраты на выпуск единицы продукции при увеличении масштабов производства: затраты на производство у единиц оцениваются величиной у утУ2 для бих игроков.
Наконец, максимальные производственные возможности обоих игроков равны у (поэтому цена и затраты неотрицательны). В случае а) получаем следующую игру:
*і = ** = [0, 1/2], ui(xi,x2) = xl(\x) ~xi, і=1,2.
Легко вычислить наилучший ответ игрока і на стратегию X/ игрока / (поскольку ,- вогнута по xt).
BRі = дс, = а (*у)/0 */-§}, где а (у) = у~ у
(мы используем обозначения разд. 4 гл.

II).
Единственный /?Е-исход таков:?? = ВЛІПВЛ, = {(, I)}.
Процедура нащупывания по Курно начинается из начальной позиции (Jtj, 4), причем каждый игрок последовательно использует наилучший ответ на текущую стратегию противника:
(4. 4) (4, 4)=(а (4), 4) ? BRt (4,4) = (4, а (4)) € BR** - ,+ (х[, Xt1) = (а (xt1), xt1) € BR1 * (х[, 4) =
= (х\, а (4)) € BR2 (8)
Ha рис. 4 мы изобразили две такие последовательности.

Изобразив самостоятельно еще несколько последовательностей, читатель убедится, что из любой начальной позиции (4.4) последовательности (4, 4) и (4, 4-') сходятся к /?Е-исходу (т т) ¦ ^ качестве упражнения мы оставляем доказательство этого утверждения, а также доказательство геометрической скорости сходимости.) Скажем, что исход (у, у) является устойчивым /ve-исходом.


Обратимся теперь к случаю б). Получается следующая игра в нормальной форме:
= [0, 1/2], щ (хи *„) = *,-(I X) (-Jjf,!- *;), 1=1,2.
По-прежнему функция и; вогнута по xt и кривые наилучших ответов имеют вид
В#, = *1 = Р(*,-)0*/-^, где
і г.^- ^ 1
т при 0 у -г-,
Р (//)==S , ,
12у при 2 -
Теперь мы имеем три 1??-исхода
/?? = ??іПВ?2 = {(і, і), (і, О), (О, і-)}.
На рис. 5 мы видим, что, начиная с любого исхода д/ Ф (-І-, -i-J , последовательность (8) всегда сходится к (у, 0) или ^0,
(за конечное число шагов). Это справедливо даже в том случае, когда точка jc сколь угодно близка к точке -М , но не совпадает с ней.

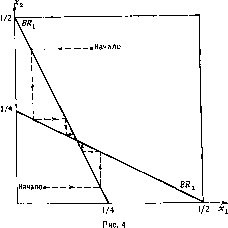
Будем говорить, что (-5-, -^ неустойчивый ME-исход, a (y , О) и ^0, у) (локально) устойчивые.


Упражнение 5
На рис. 6 представлен один из вариантов расположения кривых наилучших ответов BRit і = 1, 2, для игры со множествами стратегий Х, = Х2 = [0, 1]. Проверьте, что все три М?-исхода неустойчивы.

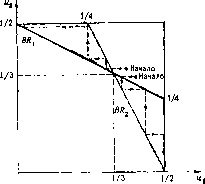
Весьма сложная структура динамической системы (8) в подобной игре проанализирована в работе Рэнд [1978].
Можно дать несколько определений процедуры нащупывания по Курно в играх п лиц: игроки могут изменять свои стратегии последовательно (порядок имеет значение) или одновременно. Соответствующие понятия устойчивости совпадают для игр двух лиц (п 2) и не совпадают в играх по крайней мере с тремя игроками (п 3) (см. упражнение 6 ниже).

Будем придерживаться второго определения.
Определение 2. Пусть множество Xt при всех і С N наделено некоторой топологией. Пусть далее G = (X;, и{; і С М) игра в нормальной форме. Предположим, что каждый игрок имеет единственную стратегию наилучшего ответа на любые стратегии остальных игроков:
для всех і € М и всех xt € X, существует единственная функция Г;(Хі)€Хі, такая, что (гДлу), xt)?BRi. (9)
С любым исходом x?Xn связана процедура (одновременного) нащупывания по Курно, начинающая из х, а именно следующая последовательность х, х\ ..., хі, ... из XN:
хі^ГіІх'Г1), i?N, t= 1,2..... (10)
Скажем, что равновесный по Нэшу исход х* устойчив в игре G, если для любой начальной позиции x??XN процедура нащупывания по Курно, начинающаяся из позиции х, сходится к х*.


Заметим, что устойчивый NE-исход в игре G обязательно является единственным равновесием по Нэшу в игре G, поскольку если начальная позиция есть равновесие по Нэшу, то процедура нащупывания по Курно приводит к стационарной последовательности.
Упражнение 6. Устойчивость процедуры последовательного нащупывания по Курно
Для заданного порядка игроков IV = {1,2, ...,п) процедурой {1, 2.....п)-последовательного нащупывания по Курно,
начинающейся из х, является последовательность
vO yl yt
I /V f f - ^ Л )
4 = r{ (x{,
, где
, 4-i, *m - - - . 4Г1). i € N, t= 1,2.....
Скажем далее, что К S'-исход х* является {1, ..., п\-устойчивым, если для любой начальной позиции х процедура {1, ..., п\-последовательного нащупывания по Курно, начинающаяся из х, сходится к х*.
1) Если п 2, то {1, 2}-устойчивость, ]2, ^-устойчивость и устойчивость согласно определению 2 совпадают.
2) Если 3, то зто разные понятия. Рассмотрим, например, игру трех лиц
f (*) = (Xi x2)2,
X, = Rf t = 1, 2, 3 ,(*) = (*,5-*:s)V
[ m3 (jf) = 3jf2 x3)2.
Единственным /?Е-исходом является точка (0, 0, 0). Докажите, что он не {1, 2, 3}-устойчив, но {2, 1, 3[-устойчнв. Является ли он устойчивым в смысле определения 2?
Достаточные условия устойчивости Ni:-исхода трудно получить, и они оказываются весьма ограничительными (см. Габе, Мулен [1980], Окугучи [1976], Розен [1965]).
Тем не менее если мы ослабим требование устойчивости таким образом, чтобы процедура нащупывания по Курно, начинающаяся около х*, в пределе давала г*, то тогда появится возможность почти полностью описать локально устойчивые У?Е-исходы.
Определение 3 (те же обозначения, что и в определении 1). Скажем, что равновесный по Нэшу исход х* локально устойчив в игре G, если для каждого і € N существует окрестность
К,- точки xf, такая, что на ?дг= X ІЛ выполнено предположе-
iSN
ние (9) и исход х* устойчив в усеченной игре (?;, м(-; і ? N).
Для того чтобы дать вычислимый критерий локальной устойчивости, предположим, что для всех і € N множество Х{ является подмножеством евклидова пространства Е{. Фиксируем равновесие по Нэшу х*, для которого xf есть внутренняя точка Х{ для всех і ? N.
Более того, предположим, что функция полезности м,- дважды непрерывно дифференцируема (С2-дифференцируема) в окрестности xf и что матрица вторых производных задает отри-
дхі
цательно определенный оператор в х* (следовательно, (9) выполнено в подходящей окрестности х*).
Определим линейный оператор Т из EN = X Ej в себя:
іб N
для всех е$Еп! Т,(е)= ? ("ГТ-У*аЖ'е/ (11)
І 6 N\U) ' дхі / ‘ XI
Где все производные посчитаны в х*.
Теорема 3. Предположим, что все собственные числа оператора Т по модулю меньше 1. Тогда х*локально устойчивый NE-ucxod.
Предположим, что х*локально устойчивый NE-ucxod. Тогда все собственные числа оператора Т по модулю меньше либо равны 1.
ди; дх;
в точке
С1дифференЦи-
Доказательство. Поскольку функция д2иі
то по теоне вырожденаруема, а матрицадх\реме о неявной функции г, (локально в X*) есть (^-дифференцируемая функция, действующая из ХЛЧ{,} в Х-. Следовательно, система (10) может быть локально записана какгде f есть С1-дифференцируемое отображение EN в себя.
По предположению х* неподвижная точка отображения /. Значит, из элементарного результата для динамических систем (см., например, Ортега, Рейнбольдт [1970]) получаем, что х* является локально устойчивым решением (12), если все собственные числа оператора f (**) по модулю меньше 1. Обратно, если хотя бы одно собственное число оператора /' (х*) по модулю больше 1, то исход х* не является локально устойчивым. Оставляем читателю проверку справедливости равенства Т f' (х*).
Следствие. Пусть п = 2, а множества Хі и Х2 одномерные. Предположим, что х*NE-ucxod в игре G = (Xit Х2, щ, и2), причем выполнены следующие условияі
1) xfвнутренняя точка Xit
2) функция U; Са-дифференцируема в окрестности х*,
3) (**) -
дх{
Тогда получаем
1 д2и, дги
д2щ д2и2 дх! ’ дх! д2иі д2и2 дх! дх!
=Флг* локально устойчива,
=$х* не является локально устойчивой
дхг дх2 д2и2
I дх і дхз I д2щ
I дхі дх2 дхі дхг
(13)
(все производные взяты в точке X*).
В предположениях следствия множества наилучших ответов BRt являются двумя кривыми класса С1, пересекающимися в х**



Содержание раздела