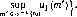d9e5a92d

СЛОЖНОЕ ПОВЕДЕНИЕ

Каждый стреляет оптимально, когда і (/) + а2(0= 1.
Упражнение 2
Обобщите теоремы 2 и 3 для класса квазиантагонистических игр1) двух лиц (Хь Х2, ии и2), которые определяются следующим образом:
любой исход игры оптимален по Парето, т. е.
Ух, г/€Х,хХ2: [ых (х)и, (у)] ФФ [и2 (/) и2 (х)].
Упражнение 3. Бесшумная дуэль
В этом варианте приведенной выше игры выстрел игрока не слышен для его противника и тот узнает о нем, лишь если он его поражает.
1) Докажите, что соответствующая функция выигрыша имеет вид (Х1 = Х2 = [0, 1]):
если хх х2, если х1 = х2, если х2 xt.
Ч (*і)а2(х2) + аг (xt)-a2 (х2),
(хХ) х2)
1 (%і) ^2
(АГі)а. (х2) о, (хд’й2 (xt),
2) Предположим, что функция аха2 -\-а1-а2 монотонно возрастает по t, a ata2at-a2 монотонно убывает.
Сосчитайте гарантированные выигрыши обоих игроков и докажите, что они не совпадают. Более точно, если ?цена шумной дуэли (пример 7), то докажите, что
sup inf их u inf sup щ.
Х\ Xs Х2 Хі
Упражнение 4
Пусть (Хі, Х„ и,) симметричная игра двух лиц с нулевой суммой, т. е. Хі = Х2; иДхх-, х2)= щ(х2, х4) для всех xit х2. Докажите, что ее цена (если таковая имеется) равна нулю, а множества оптимальных стратегий совпадают.
Задача 6 (Мулен [1976])
Для любых действительных чисел a, b, с, d следующая игра двух лиц с нулевой суммой, в которой у каждого игрока четыре стратегии, имеет цену. Матрица выигрышей для игрока,
!) В отечественной литературе принят термин: игры с противоположными интересами. Прим, перед.
выбирающего строки, имеет вид
b
с
a + ft+e+d 4и a-\rb-{-c-\rd4
Более того, цена val (G) игры G удовлетворяет неравенствам sup {inf (а, b), inf (с, d)} val (G) inf {sup (а, в), sup(b, d)}.
Дайте интерпретацию.
Задача 7 (Шепли)
Пусть G = (Xx, Х2, щ) конечная игра двух лиц о нулевой суммой. Предположим, что для каждого двухэлементного подмножества Y( множества Х(, і= 1, 2, игра (Yt, Y2, щ) имеет цену.

Докажите, что в этом случае игра G также имеет цену.
Задача 8
Пусть (X,, Х2, () игра двух лиц с нулевой суммой. Обозначим через ftj = X* (соответственно R2 = Xf') множество стратегийответов первого игрока (соответственно второго игрока). Докажите следующие равенства:
sup inf Ui(xit х2) = inf sup щ(хи ГД*!)),
*,6Х, xseX, 'teRtxteX,
inf sup Щ (Xf, X2) = sup inf Uf (Гі (x2), x2).
x2€X2x,eX, i.,ex,
Каковы оптимальные стратегии в игре (Rf, Х2, и(), где Щ (гі, xt) = щ (г, (х2), *2)?
2) Предположим, что ХІ( Х3выпуклые компакты. Обозначим через RiczRi (соответственно R2czR2) множество непрерывных функций из Х2 в X, (соответственно из X, в Х2).
Докажите следующие неравенства:
SUp inf Uf ^ SUp inf Uf (rt (xs), xj ^
*t хг r, e R\ x*
inf sup Uf (Xf, r2 (Xf)) inf sup Щ
r,e Rc x *1
(используйте теорему Брауэра: непрерывное отображение выпуклого компакта в себя имеет по крайней мере одну неподвижную точку).
3) Приведите пример, в котгором Х, = Х2 = [0, 1], uf непрерывна и тем не менее
sup inf Ы( = sup inf і inf sup щ inf sup щ.
x, x% rse xi x‘ x
ЛИТЕІРАТУРА
Грин, Лафон (Green J., Laffont J. J.)
[1979] Incentives in public decision making. Studies in public economics, vol.

1, Amsterdam, North-Hollland Publishing Co.
Keih (Case J. H.)
[1979] Economics and the competitive process. New York, University Press.
Льюс, Райфа (Luce R. D., Raiffa H;.)
[1957] Games and decisions, New York,, J. Wiley. [Имеется перевод: Льюс P. Д., Райфа X. Игры и решения.. М.: ИЛ, 1961.]
Мулен (Moulin Н.)
[1976] Prolongement des jeux a deux joueurs de somme nulle. Paris, Bulletin de la Societe Mathematiquie de France, Suppl.

Memoire 45.
[1980] On strategy-proofness and siingle peakedness. Public Choice, 35, 437455.
[1981] Prudence versus sophistication in voting strategies. Journal of Economic Theory, 24, 3, 398412.

СЛОЖНОЕ ПОВЕДЕНИЕ

Осторожное поведение игроков основано на предположении об их полной изолированности, согласно которому каждый игрок ориентируется только на свою собственную функцию выигрыша и не обращает внимания на функции выигрыша остальных игроков. В этой главе исследуем, напротив, случай полной информированности, когда каждый игрок знает все функции выигрыша.

При некооперативном поведении игроков это порождает взаимные стратегические ожидания следующего вида: игрок і ожидает, что все другие игроки / исключат свои доминируемые стратегии.
На основе этого ожидания, возможного благодаря полной информированности, у некоторых игроков могут возникнуть новые доминируемые стратегии и т. д.
Сложное поведение будет определено сначала для игр в нормальной форме (разд. 1), затем эквивалентным образом для игр в развернутой форме (разд. 2).

В разделах 3, 4 и 5 демонстри-руются некоторые приложения теоремы Куна.
1. ПОСЛЕДОВАТЕЛЬНОЕ ИСКЛЮЧЕНИЕ ДОМИНИРУЕМЫХ СТРАТЕГИЙ
Пример 1. Выборы большинством голосов с решающим игроком при равном числе голосов (Фаркуареон [1969]).
Сообщество 11, 2, 3} должно выбрать одного из трех кандидатов {а, b, с}. Правило голосования есть правило большинства, при этом голос игрока 1 оказывает решающее влияние при равенстве голосов. Другими словами, множество стратегий (множество предложений) имеет вид Х,= {а, Ь, с} для і =1, 2, 3. Если игроки выдвинули кандидатуры {хи х2, х8}, то выборы происходят по правилу


Предположим, что функции выигрыша игроков при избрании того или иного кандидата имеют следующую структуру (парадокс Кондорсе1)):
Щ (с) щ (Ь) (а),
и2 ф) 2 (а) и2 (с),
з (а) з (с) а Ф).
В игре трех лиц в нормальной форме (Xf, Х2, Х8, щоп, и2ощ ияоп) каждый игрок имеет единственную лексикографически осторожную стратегию (см. задачу 5 гл. I), а именно голосовать за наиболее предпочтительного для себя кандидата.

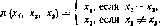
Следовательно, лексикографически осторожное поведение приведет к избранию кандидата а. При условии полной информированности ситуация будет совершенно другой. Заметим, что стратегия х2 = Ь игрока 2 доминируется (стратегией х\ с) и что стратегии а и с не доминируемые, но и не эквивалентные;
и2ол ф, а, с) = и2 ф) и2 (с) = игоп ф, с, с), и2ол ф, а, а) = и% (а) и2 ф) = и2ол ф, с, а).
Значит, й)2(и2) = {а, с}, и аналогично ?Ds(ua) = {b, с}. С другой стороны, игрок 1, чей голос разрешает спорные ситуации, имеет доминирующую стратегию, а именно а (проверку этого факта оставляем читателю). Таким образом, если считать, что игроки не будут использовать доминируемые стратегии, то множества стратегий сузятся до
Уі = Iй} n = k с), Yt = {b,c}.
При данном усечении множеств стратегий для игрока 2 стратегия а теперь доминируется стратегией с и поэтому может быть исключена:
и2ол (а, а, х3) ы2ол (а, с, х9)
для xa = b, с, и неравенство становится строгим при хя = с.
Аналогично стратегия b игрока 3 теперь доминируется стратегией с:
и3оп(а, х2, b)^.uaon(a, х2, с)
для х2 = а, с, неравенство становится строгим при х2 с.
Следовательно, после двух раундов исключения доминируемых стратегий у каждого игрока останется по одной стратегии и кандидат с будет избран, несмотря на то что он является наихудшим для игрока 1! Следовательно, право первого игрока
!) Классический пример того, что для большинства членов сообщества исход а лучше исхода b, Ь лучше с и с лучше а,Прим, перев.
разрешать спорные ситуации оказывается его слабым пунктом в игре, потому что оно дает возможность сразу предвидеть его стратегический выбор.
Определение 1. Для игры в нормальной форме G = = (Хг, мг; і € N) последовательное исключение доминируемых стратегий означает построение последовательностей X,- = = X^XJz)... zX-zX(+tz... для всех i g N, где Х(+1 = = Ч i?N).
Скажем, что игра G разрешима по доминированию, если существует целое t, такое, что для всех і функция выигрыша и,- не зависит от xt на X‘N:
Уі g X\, VxtZX't Ui(xit xt) = ut(yh xt). (1)
В этом случае назовем Ху множеством сложных равновесий в игре G.
Ясно, что если (1) выполнится для некоторого t (и некоторого tgX), то Х = Х-+1=..., поэтому если игра разрешима по доминированию, то выбор конкретного t не изменит множества X‘N. Следовательно, множество сложных равновесий определено корректно. Для того чтобы получить стратегию, соответствующую сложному равновесию, каждый игрок і должен найти последовательности X), t ? N для всех / ? N, полностью 'использовав таким образом знание функций выигрыша. Эти вычисления производятся независимо каждым игроком в предположении, что остальные игроки делают то оюе самое.

Только в этом ограниченном смысле сложное поведение может быть названо изолированным.
Разрешимость по доминированию игры G, означает, что после конечного числа раундов исключений все стратегии каждого игрока станут для него эквивалентными (ионе для других. См. пример 3, гл.

I). Если функции выигрыша для всех игроков взаимно однозначны на XN, то множество сложных равновесий (если оно существует) состоит из одного элемента.

Следовательно, в таких разрешимых по доминированию играх сложное поведение игроков детерминированно.
Сложное равновесие обобщает равновесие в доминирующих стратегиях в следующем смысле.
Лемма 1. Если в игре G множество D равновьсий в доминирующих стратегиях не пусто, то игра G разрешима по доминированию и D есть множество сложных равными
Доказательство сразу следует из леммы 2, г-л і Если только у одного игрока I есть доминирующ351 стратегия, то, очевидно, D{ (,¦) является і-й компонентой множест.ва сложных равновесий, если последнее существует.
Для игры в нормальной форме не известны достаточные условия разрешимости по доминированию. Для того чтобы получить такие условия, необходимо использовать другое представление игры, а именно развернутую форму.
2. ИГРЫ В РАЗВЕРНУТОЙ ФОРМЕ И ТЕОРЕМА КУНА
Пример 2. Выборы с правом вето
Пусть сообщество N = {1, 2, 3} выбирает одного кандидата из множества А = {а, Ь, с, d}. Правило голосования таково: начиная с игрока 1, каждый игрок последовательно налагает вето на выбор кандидатуры одного из неотведенных кандидатов.

Единственный оставшийся кандидат считается избранным.
Пусть заданы функции выигрыша игроков ии 2, us на множестве А. Возникшая ситуация описывается игрой в нормальной форме:
Множество Хі А\ стратегия игрока 1 состоит в объявлении кандидата, на избрание которого он первым накладывает вето.
Множество Хг состоит из отображений хг из А в А, таких, что х2(а)фа для всех а$А. Стратегия х2 означает, что если игрок 1 уже наложил вето на кандидата а, то игрок 2 после этого накладывает вето на кандидата х2 (а).


Множество Х3 состоит из отображений х3, которые определяют для пары (а, Р), уже отведенных кандидатов, кандидата х3 (а, Р) € Л\{а, РЬ которого отводит игрок 3.
Исход, соответствующий данной тройке (% х2, ха) ? €ХйхХ2 X Х3, определяется так:
Я (Xj, Х2, Х3) = Х2 (Х(), Хд (Х{, Х2 (Xj)).
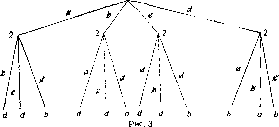
Нормальная форма игры представима в следующем виде: (Xj, Х2, Ха, ихол, 2ол, ЦдОя). Язык теории графов более удобен; на рис. 1 изображена развернутая форма игры;
Каждой нефинальной вершине этого дерева игры соответст-вуетг некоторый игрок, имеющий право выбирать любую из следующих вершин. Каждая финальная вершина определяет избранного кандидата. Предположим теперь, что функции вц-

игрыша удовлетворяют следующему условию:і (d) щ (с) и, ф) щ (а),
2 Ф) 2 (Ф 2 Ф) 2 (). (2)
з Ф) з И з Ф) 3 ($-
Вначале заметим, что игрок 3 имеет доминирующую стратегию: он отводит менее предпочтительного для себя кандидата из двух еще оставшихся в списке.
Это определяет единственный элемент xf из Х3. Далее отметим, что ни у первого, ни у второго игрока нет доминирующей стратегии.

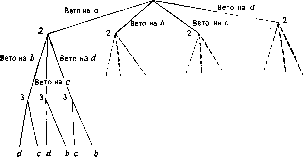
В самом деле, во множестве Xf ни одна стратегия не доминируется, поэтому (щ) Хі. Для того чтобы проверить это, докажем, например, что стратегия первого игрокаотвести наилучшего для него кандидата ане является доминируемой. Рассмотрим следующие стратегии х2 ? Х2, х3 ? Х2:¦^2 Ф) ^3 Ф* d) ==
- . . , - . . [ Ь, если а, Фа, Ь,
*.( ) = а Для всех а фа, хі (а, а) = і ^ ^ а = {
Тогда иіо%(а, хг, х3) = ф) игоп (а, хг, хя) при а Фа, т. е. xt = aнедоминируемая стратегия игрока 1.
Аналогично можно проверить, что игрок 2 имеет 24 недо минируемых стратегий среди З4 элементов множества Х2: стратегия х2 принадлежит множеству (м2) тогда и только тогда, когда для всех хх € Хі кандидат х2 (хг) не является наилучшим Р9 функции ц, среди кандидатов из множества АХ^}.
Второй раунд исключения доминируемых стратегий позволяет игроку 1 с пользой распорядиться имеющейся у него информацией. А именно, если игрок 1 будет сугубо осторожен и наложит вето на наихудшего для него кандидата d (Р2 (их) = {d}), то произойдет избрание кандидата b (поскольку функции выигрыша игроков 2 и 3 на исходах а, Ь, с определяют один и тот же порядок, то b будет избран при любой паре недоминируемых стратегий: b = n({d}x2(u2)x{x%})).
Однако игрок 1 может надеяться на лучший исход, чем избрание Ь. В самом деле, если на b наложить вето, то для игроков 2 и 3 возникнет следующая игровая ситуация.


Если игрок 2 не обращает внимания на функцию выигрыша игрока 3, он при осторожном поведении наложит вето на с (Р2 (и2) = {х2}, где для всех хх кандидат х2 (лу) является наихудшим по и2 среди ЛХІлу}), тем самым навязывая избрание d, что означает полное поражение игрока 1. Если, напротив, игрок 2 достаточно хорошо информирован, то он имеет возможность предвидеть поведение игрока 3, и в этом случае оптимальным является вето на d, обеспечивающее избрание а.
Возвращаясь к последовательному исключению доминируемых стратегий, мы обнаруживаем, что после двух раундов исключения стратегий игроки 2 и 3 имеют полностью определенные стратегии (xl = {x*}, х = {*?}), а после трех раундов игрок 1 также остается с единственной стратегией, таким образом исход игры при сложном поведении есть избрание кандидата а.
Определение 2. Конечное дерево есть пара Г = (М, о), где Мконечное множество вершин, а а сопоставляет каждой вершине ее ближайшего предшественника, причем:
- Существует единственная вершина т0, такая, что о (m0)=m0. Назовем ее начальной вершиной.
- Существует целое I, такое, что о1 (т) = т0 для всех т$М, Наименьшее такое I назовем длиной дерева Г.
Вершина т, для которой о_1(т) = 0, называется финальной вершиной Г, а множество таких вершин обозначается через
Т (Г). Для нефинальных вершин пг множество о'1 (пг) состоит из преемников пг, т. е. из следующих за m вершин.
Определение 3. Пусть N заданное конечное сообщество. Игрой в развернутой форме со множеством игроков N называется следующая совокупность:
- Конечное дерево Г = (УИ, а).
- Разбиение (М,-),-6д/ множества М\Т (М).
- Для каждого игрока і ? N функция выигрыша и,- из Т{М) в R.
Разбиение (Mfo € n определяет, какой игрок ходит в каждой конкретной нефинальной вершине. Если m0?Mh то игра начинается с того, что игрок і должен выбрать преемника т0, т. е. следующую за т0 вершину, скажем вершину тх из а-1 (т0).

Если тг?Т (М)финальная вершина, то игра окончена и выигрыши игроков суть иД/Пх) при igiV. Если m1(j:T (М) нефинальная вершина, то игрок /, для которого mx € М/, имеет право хода и выбирает следующую за т1 вершину, скажем ma€~l(mi) и т- Д-


Отмеченные вершины являются финальными. Заметьте, что по нашему предположению на каждом шаге игры игрок, делающий ход, имеет полную информацию о текущей вершине и общей структуре игры: это предположение обычно характеризуется как полная информация.
Теорема Куна утверждает, что конечная игра в развернутой форме в общем случае разрешима по доминированию и что в ней легко может быть вычислен исход сложного равновесия. Для того чтобы это продемонстрировать, рассмотрим описанную выше игру: выборы с правом вето (пример 2, рис.

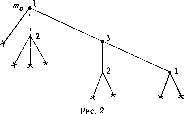
1). Поскольку во всех вершинах, предшествуюш.их финальным, ходит игрок 3, то остальные игроки, зная его функцию выигрыша из (2), могут предвидеть его поведение.

Это позволяет редуцировать игру, изображенную на рис. 1, к следующей:


Поскольку в этом новом дереве во всех вершинах, предшествующих финальным, ходит игрок 2, то игрок 1 может предвидеть результат этих ходов по функции и2, и в итоге получается игра с одним участником первым игроком.

Предлагая отклонить кандидата Ь, игрок 1 реализует стратегию, являющуюся компонентой сложного равновесия.
Приведенная выше попятная процедура может быть обобщена для любой игры в развернутой форме при довольно слабом предположении о взаимной однозначности.
Определение 4. Пусть G = (M, a; M-t, up i?N) игра в развернутой форме, такая, чю для любых т, т' ?Т (М) имеем
[Эі € N Ui (m) = и,- (/n')]=? [V/ € N u,(m) = u/ (m')]. (3)
Пусть L(M) множество вершин, для которых все последующие вершины являются финальными:
m?L (М) (т)аТ (М).
Тогда игре G соответств/ет редуцированная игра G* =s = (M*t о*; Mf, up, i g N), в шторой
- множество вершин определяется равенством М* = =М\Г0(М), где T0(M) = {nitT(M)\e(tn)?L(M)};
- отображение о* есть сужение а на М*\
- финальные вершины дерева (М?, о*) таковы:
T(M*)^L(M)U{T(M)\T0{M)}-
- М* = Mt П { M* \ T (M*)}, значит, (Mf)t е N разбиение М*\Т (М?);
- функция выигрыша и? имеет вид
если пг?Т (М)\Т0 (М), то и? (т) = щ (т),
если m ? L (Af) и mg МЛ то uf (т) иг (mj), где тj оптимальная для игрока / следующая за m вершина; U/(tn,)= sup и,(т').
m'ea-1 (m)
Лемма 2. Если {М, о)дерево длины I, то дерево (М*, а*) имеет длину (I1).
Доказательство леммы 2. Заметим сначала, что множество L (М) не пусто. Если оно пусто, то для каждой нефинальной вершины т множество о-1 (т) содержит хотя бы одну нефинальную вершину, и поэтому мы можем построить бесконечную последовательность различных вершин т0, Ші, .... mt, ..., где mt+i €-1 (Щ)\ это противоречит тому, что длина дерева (М, о) конечна. Выберем далее вершину т, такую, что
о1 (т) = т0, о1~х (т) Ф т0. (4)
Такая вершина существует по определению I. Предположим, что a(m)^L(M). Тогда найдется вершина т'?М\Т(М), такая, что a(m’) = a(m). Выбирая любую вершину m" go-1 (m'), получим о2 (т) = а (т), следовательно, о‘ \т) = а1-1 (т) Ф та.

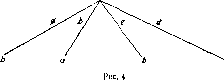
Получили противоречие. Итак, мы доказали, что a(m)^L(M). Ввиду того что вершина т является финальной, приходим к заключению, что т?Т0(М). Поэтому никакая вершина, удовлетворяющая (4), не может входить в М* и, следовательно, дерево (М*, о*) имеет длину, не превышающую (/1).

Легко показать, что (М*, о*) имеет длину в точности (I1).
Алгоритм Куна состоит из последовательных редукций игры G. После этих / редукций дерево игры (М*1, о*1) имеет длину 0, т. е.'М*1 = {тб), а о*1тождественное отображение. Обозначим через 0(. uf1 (та) (единственное) значение выигрыша игрока і в G*1.
Теорема 1 (Кун). Пусть G = (M, о; МІУ ы;; і ? Ы)игра в развернутой форме, для которой выполнено условие (3). Тогда
игра G, рассматриваемая как игра в нормальной форме, разрешима по доминированию, а выигрыши N, соответствующие сложному равновесию, задаются алгоритмом Куна.
Доказательство. Вначале уточним, что мы понимаем под нормальной формой игры G. Поскольку игрок і должен принять стратегическое решение в каждой вершине множества Mt, то Стратегией х{ будет отображение из Mt в М, причем такое, что
хДт) €т-1 (т) для всех т?М{.
Пусть Х{ множество таких отображений. Заданный набор х(х,)і6л/ порождает партию т0, ..., тк, где
- тв€М1,^ті = Хі'(т0)
- m1^T(M)=^k l
- m1 € Mit =om2 = xtl (mf)
- mt?T (M) = k t
- mt€Mit=$mt+i = xit(mt), и соответствующие выигрыши задаются равенством ui(x)=U;(mk). Мы должны доказать, что игра (Х(, up, i g N) разрешима по доминированию и выигрыши игроков в сложном равновесии определяются алгоритмом Куна. Редукция игры G к игре G* (определение 4) позволяет выкинуть все вершины из Т0(М), превращая вершины из L(M) в финальные и приписывая вершине m из L (М) П Mt вектор выигрышей, который соответствовал'бы оптимальному ходу игрока і в вершине т. Далее, пусть А[ обозначает следующее подмножество множества Хр


Тогда игра в нормальной форме (А{, up i?N) изоморфна редуцированной игре G* (заметим, что если игрок і безразличен по отношению к двум каким-либо следующим за m € L (М) П М, вершинам, то в силу (3) и все остальные игроки безразличны к выбору из этих вершин, а потому соответствующие стратегии во множестве А{ могут быть отождествлены). Заметим теперь, что стратегия х(-?Х;\Л; является доминируемой стратегией игрока і (в самом деле, xt доминируется стратегией у{ € А{, совпадающей с х, на множестве Mt \ L (М)). Итак, мы имеем
?D{ (u^aAiCzXj.
Теперь мы используем следующую основную лемму,
Лемма 3 (Роше [1980]). Пусть G = (X{, up i?N) конечная игра в нормальной форме, причем для любых двух исходов х, х' ? X выполнено
[i i?N u-t (х) = ut (*')]= [V/ g N /(*) = ,(*')]- (6)
Пусть далее для всех і ? N множество Л, является подмножеством X;, удовлетворяющим условию (5).
Тогда игра G разрешима по доминированию (d-разрешима) в том и только в том случае, если игра Н = (Л;, up, i?N) разрешима по доминированию, а векторы выигрышей, соответствующие сложным равновесиям, совпадают.
Применяя индуктивно лемму 3, получаем G d-разрешима фф G? d-разрешима фф G** d-разрешима ФФ.. и все эти игры имеют одни и те же векторы выигрышей в сложных равновесиях. Поскольку игра G*1, очевидно, d-разрешима и ей соответствуют равновесные выигрыши (РДел/. теорема 1 полностью доказана.
Лемма 3достаточно важный результат: в процессе последовательного исключения доминируемых стратегий некоторые игроки могут оказаться ленивыми и не исключить всех своих доминируемых стратегий или исключение может производиться последовательно (сначала игрок 1 исключит доминируемые стратегии, потом игрок 2 и т. д.), тем не менее разрешимость по доминированию сохранится, а вектор выигрышей в сложных равновесиях не изменится. Этот результат существенно повышает доверие к понятию сложного поведения.
Упражнение 1
Приведите пример игры в развернутой форме, для которой не выполнено предположение (3) об однозначности и соответствующая игра в нормальной форме не разрешима по доминированию.
Задача 1. Доказательство леммы 3 (Гретлейн [1980], Роще [1980])
Пусть игра G = (X{, up, igN)фиксированная конечная игра в нормальной форме с условием (6) и для игры Н = (Л;, up і € N) выполнено условие (5).
Положим XX, = XN), ЛХ= X ?D(u{, AN).
IS N i6 N
1) Если стратегии х{ и у{ игрока і эквивалентны для игрока і в игре G, то в силу (6) получаем
?/€ W, V*,gXf uj {xh xt) = uJ{yi, Xf),
Выведите отсюда, что если отождествить эквивалентные стратегии каждого игрока в игре G, то это не повлияет на d-разре-шимость игры.
2) Отождествляя соответствующим образом стратегии игроков, эквивалентные в игре Я, и используя условие (5), покажите, что
AfcX'icA;, i?N.
3) Завершите доказательство леммы 3, последовательно применяя при построении множеств AlN и X‘N утверждения п. 1 и 2.
3. ИГРЫ ДВУХ ЛИЦ С НУЛЕВОЙ СУММОЙ
Вначале докажем вспомогательный результат.
Лемма 4. Пусть G = (Xit Х2; Uj)игра двух лиц с нулевой Суммой и конечными множествами стратегий. Тогда сложное равновесие в игре G есть седловая точка по функции щ. Следовательно, разрешимые по доминированию игры двух лиц q нулевой суммой имеют цену.
Доказательство. Для данных подмножеств УіСгХ^ У2сгХ2 обозначим через S (Уь У2) множество седловых точек (возможно пустое) в игре (Уь У2, ut). Далее положим
Zi = Si(ui\ Yu У2).
Пусть (xit х2)седловая точка в игре (ZL, Z2, и,), и предположим, что (*1, х2) не является седловой точкой в игре (Уі, У2, щ).



Содержание раздела