Прибыть магазина
Из него можно видеть, что при снижении цены Р0 в магазине с ивдексом О величина спроса на его товар при неизменных ценах Р1 соседей конкурентов возрастает.
Из выражения (4.25) можно получить уравнение взаимосвязи цены и величины спроса на товар, предлагаемый магазином с индексом О:
і=я+-гА (4*26)
0 1 N L
Выручка магазина с индексом О можно определить как
(4.27)
TR0=R0xQ=(Rl+^-2t^)xQ0,
где TR(j выручка, валовой доход магазина с индексом О.
Прибыть магазина с индексом О определяется как разность выручки (выражение (4.27)) и издержек (выражение (4.15)) следующим образом:
TR,=R0xQ0-TC = (Rl+jt-2t^)xQ0-(FC + AVCxQ0), (4.28)
где t стоимость поездки в магазин за единицу расстояния; L число домохозяйств в городе; N количество магазинов в городе; FC средняя величина постоянных издержек магазина.
Необходимое условие максимизации прибыли магазина будет иметь вид:
Из уравнения (4.29) легко получить величину объема продаж, максимизирующего прибыль магазина:
Qo=^ + ^x(A-AVC), (4.30)
Из функции спроса (4.26) и выражения (4.30) получим выражения для величины цены, максимизирующей прибыль магазина:
„с „ 2і 2t . L L ,T„41 Py-AVC t
P п=Р,+---x + x(i? -AFC) ] = -+ , (4.31)
0 1 N L 2N At 1 2 N’
где P цена, обеспечивающая максимизацию прибыли в магазине с индексом 0; Ру цена в соседних магазинах; t стоимость поездки в магазин за единицу расстояния; L число домохозяйств в городе; N количество магазинов в городе; А ?С средние переменные издержки магазина с индексом 0.
Из полученного выражения следует, что оптимальная по критерию максимизации прибыли магазина цена Р возрастает с ростом цены Ру, устанавливаемой соседним магазином, а также с увеличением транспортного тарифа t. Количество продаж 2; возрастает с увеличением цены конкурента и сокращается с ростом транспортных расходов покупателей.
Предположим, что все магазины имеют одинаковые функции издержек и равный доступ на рынок. Тогда цена и количество продаж окажутся одинаковыми для всех магазинов города. Заменим в выражении (4.31) Ру и Р на Ри получим:
Р = + А?С. (4.32)
N
Заменим в выражении (4.30) Ру на Р, определяемое выражением (4.32), и получим:
Из выражения (4.33) следует, что при равенстве цен во всех магазинах точки безразличия покупателей в отношении всех магазинов будут равномерно распределены по окружности, и на долю каждого магазина првдется часть рынка, равная 1/JV. Экономическая прибыль каждого магазина при этом составит:
П = PQ - {FC + A VC x Q )= ( + A VC) - {FC - A VCx ) =
(4.34)
N N= Щ-FC,
N2
где FC средняя величина постоянных издержек магазина.
Из выражения (4.34) следует, что прибьть может оказаться как положительной, так и отрицательной. При положительной экономической прибыли возникает вопрос: приведет ли тогда свободный вход в отрасль новых конкурентов к падению прибыли до нуля, как это имеет место, например, в модели совершенной конкуренции.
Возможность вхождения в отрасль. Ответ на этот вопрос зависит от того, сколь велика в постоянных издержках доля поглощенных затрат.
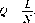
Поглощенные затраты это издержки, которые никогда не будут возвращены, если предприятие покинет отрасль. Например, если предприятие затратило на геологоразведку определенную сумму, но результаты поиска показали отсутствие полезных ископаемых в изученном районе, затраты на геологоразведку будут безвозвратно поглощенными.
Размещение нового магазина в уже поделенном на N секторов рынка городе на окружности может быть затруднено. Поскольку магазины размещены равномерно вдоль линии окружности города, их местоположение не может бьнь изменено без некоторых потерь, связанных с перемещением на новые места.
Наилучшим было бы размещение нового магазина на полпути между парой соседних действующих магазинов. В этом случае его клиентура составляла бы половину клиентуры занявших более выгодное положение магазинов. При неизменной цене его выручка оказалась бы вдвое меньше, чем удругих магазинов города.
Поэтому, возможно, что новичок не получит положительной экономической прибыли, тогда как укоренившиеся на рынке магазины будут рентабельны.
Модель города на окружности и модель Чемберлина. Принципиальное отличие пространственной модели монополистической конкуренции от модели монополистической конкуренции Чемберлина заключается в следующем.
В модели Чемберлина любое предприятие, в том числе новичок, получает пропорциональную долю рыночного спроса и в итоге их прибьть в длительном периоде сводится к нулю как и в случае чистой конкуренции.
В модели пространственной конкуренции с фиксированным местоположением уже функционирующих продавцов возможности новичка менее привлекательны по сравнению с перспективами действующих предприятий. В этой модели совершенная свобода входа на рынок совмещается с наличием положительной экономической прибыли в длительном периоде.
Однако описанное различие довольно относительно. Например, уличные торговцы не понесут существенных поглощенных издержек, связанных с фиксацией их положения на местности.
Если на рынке появится еще один новый уличный торговец, другие могут счесть возможным изменить местоположение так, чтобы восстановить равномерность своего распределения в рыночном пространстве. В этом случае возможности получения прибыли новичком будут ничуть не меньше, чем у ранее укоренившихся на нем торговцев.
Избыточное разнообразие. В рассмотренной пространственной модели монополистической конкуренции модели города на окружности экономическая прибыль в длительном периоде может оказаться и положительной, и нулевой.
При свободном вхождении в отрасль при монополистической конкуренции, как и при чистой конкуренции в долгосрочном периоде, количество предприятий возрастает, что сводит к нулевому значению экономическую прибыль предприятий.
В рассмотренной пространственной модели города на окружности при нулевой величине прибыли в долгосрочном периоде определить количество магазинов можно из выражения (4.34). Приняв величину прибыли нулевой (П = 0), получим следующее количество магазинов в долгосрочном периоде:
Оптимальное количество магазинов, которое обеспечивает минимум затрат покупателей при совершении покупок в магазинах модели города на окружности, определяется выражением (4.19) как:
yjltL/FC л JV ~4tL/2FC~ '
Таким образом, в пространственной модели монополистической конкуренции модели города на окружности количество магазинов может бьиь в два раза больше, чем это необходимо для обеспечения эффективного использования ресурсов при обслуживании в них и обеспечения минимума затрат покупателей. То есть, здесь имеет место избыточное разнообразие продуктов, в данном случае торговых услуг.
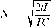
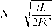
Следует обратить внимание на то, что при этом предложение услуг будет более удобным для покупателей, так как магазины для среднего покупателя будут в два раза ближе к дому.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Дайте определение (включая формулы и графики) следующих понятий:
а) модель монополистической конкуренции:
б) кривые спроса на продукт предприятия при монополистической конкуренции:
в) проблема избытка мощности:
г) модель линейного города:
д) допущения модели города на окружности:
е) избыточное разнообразие.
2. Определите цены, обеспечивающие максимизацию прибыли магазинов в модели линейного города длиной 35 ед., если расходы покупателя на доставку товара на единицу пути составляют 10 ед., расстояния от магазинов А и йдо ближайшего конца улицы 0,2 и 0,3 длины города, соответственно.
3. Определите оптимальное с позиции покупателя количество магазинов в модели города на окружности, если расходы покупателя на доставку товара на единицу пути составляют 10 ед., в городе 1000 домохозяйств, постоянные издержки магазина 50 ед.
4. Определите количество магазинов в модели города на окружности в долгосрочном периоде, если расходы покупателя на доставку товара на единицу пути составляют 10 ед., в городе 1000 домохозяйств, постоянные издержки магазина 50 ед.
