8.1. Допущения в модели Солоу.
Абстрагирование от государственного влияния связано еще и с тем, что интерес представляют величины совокупного спроса на потребительские и инвестиционные блага, а не конкретное соотношение спроса со стороны общественного и частного секторов.
2) На рынке товаров идентичные предприятия производят гомогенное благо Y(t), причем может производиться как средство производства I(t), так и предмет потребления C(t). Предприятия преследуют цель максимизации прибыли. Господствует совершенная конкуренция на рынке товаров.
Цена блага Y(t) постоянна и упрощенно принимается за единицу. Это позволяет агрегировать множество различных благ в экономике к гомогенной величине, такой, как реальный ВВП.
3) Домохозяйства предлагают свои факторы производства -труд L(t) и капитал K(t) неэластично по цене. Господствует совершенная конкуренция на рынках факторов производства, и цены обоих факторов - реальная ставка оплаты труда W(t), так же как и реальный процент г (t) - доход фактора капитала, под которым в модели Солоу понимается процент на вложенный капитал, - являются гибкими.
Допущение о ценовой неэластичности предложения производственных факторов служит для упрощения анализа. При таком допущении рынок факторов в любом периоде стремится к уровню полной занятости и существует четкая цена равновесия, которая приводит в равенство спрос и предложение.
4) Предложение труда растет с экзогенно заданной постоянной ставкой n. Ставка оплаты труда (доход фактора труда) является постоянной, так что n одновременно можно представить как темп роста населения.
Упрощенно данное допущение можно понять таким образом, что нет разницы между трудоспособным и всем населением. Поскольку в классическом случае при предпосылке функционирующих рынков факторов производства не может возникнуть вынужденная безработица, то, следовательно, каждое домохозяйство занято в экономике.
5) Инвестиции I(t) состоят из чистых инвестиций и амортизационных отчислений. Они, по определению, измеряют брутто-изменение основного капитала K(t) во времени:
K(t) = I(t) - SK(t), (1)
где 5 - экономическая норма амортизации 0.
Размер инвестиций в неоклассической модели роста определяется на рынке товаров и капитала величиной агрегированных сбережений.
6) В любой момент времени сберегается постоянная часть национального дохода. Норма сбережения определяется как:
S (t) = sY(t), s е [0, 1]. (2)
При этом предполагается, что S = I.
7) Технология производства. Субституциональные производственные возможности описываются следующей линейно-гомогенной двусторонней непрерывно дифференцируемой производственной функцией типа Кобба-Дугласа со степенью гомогенности г = 1:
Y(t) = F[K(t), L(t)], (3)
где F (L), F (K) 0.
Производство характеризуется постоянной отдачей от масштаба. Для всех X действительно, что AY = F(AK, AL) = AF(K, L). Тем самым возможно перевести производственную функцию в так называемую интенсивную форму с = 1/ L, которая ставит производительность труда (а также и доход на душу населения) в зависимость от капиталовооруженности (основного капитала на душу населения):
y(t) = f[k(t), 1]. (4)
Напомним ключевые свойства функции Кобба-Дугласа:
- постоянная отдача от масштаба;
- разнонаправленное движение предельных производительностей труда и капитала (если MPi растет, то MPk сокращается);
- постоянное соотношение доходов факторов производства, т. е. долей капитала и труда (w/r).
8) Производственная технология подвержена так называемому условию Инады:
Lim f[k(t)] = 0 Lim f[k(t)] = 0
k ^ 0 k ^ да
Lim f'[k(t)] = да Lim f' [k(t)] = да
k ^ 0 k ^ да, (5)
т. е. фактически производство характеризуется убывающей предельной производительностью факторов производства.
9) Производство характеризуется постоянной эластичностью замещения:
о = - д (K\ L) \ д MRS ¦ MRS\ (K \ L) = 1. (6)
т. е. при однопроцентном повышении соотношения цены одного из факторов получаем однопроцентное замещение его другим фактором.
Для конкретного примера производственной функции Кобба-Дугласа в виде
V K а Т (1 - а)
Y(t) K(t) L(t)
частичная производственная эластичность соответствует а, 1 - а:
Y(t k(t)а, где а е [0, 1]. (7)
10) Факторы в рамках функционального распределения доходов вознаграждаются в соответствии со стоимостью предельного продукта, которая в условиях совершенной конкуренции на рынках факторов является ценой этих факторов:
Fk f '[k(t)] гю;
Fl д {L(t) ¦ f '[k(t)]} / dL f [K (t)] - k(t) f '[k(t)] w(t). (8)
Вследствие линеарной гомогенности производственной функции результат, свидетельствующий о распределении дохода в пользу факторов согласно их предельной производительности, полностью выполняется. Достигается теорема Эйлера (adding-up theorem):
V (t) r(t)K(t) + W(t)L(t) 1 n + l, (9)
где r(t) ¦ K (t) - суммарная прибыль; W(t)L(t) - суммарная оплата труда.
Исходя из данных допущений рассмотрим модель Солоу подробнее. Вначале представим наиболее простую ситуацию, а в дальнейшем перейдем к включению в анализ ситуации с ростом населения и влиянием технического прогресса.
Ключевым элементом экономического роста в модели Р. Солоу является накопление капитала. Норма выбытия основного капитала - экономическая норма амортизации 5 постоянна и пропорциональна капиталу.
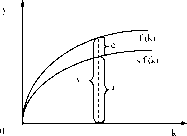
8.2.2).
Уровень запаса капитала, при котором нетто-инвестиции равны экономической норме амортизации, называется устойчивым уровнем капиталовооруженности. Обозначим его как k*.
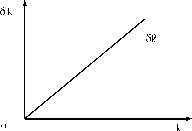
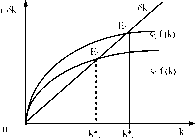
Так, рост нормы сбережений с si до s2 сдвинет траекторию кривой инвестиций вверх, что приведет к росту капиталовооруженности с к*1 до к*2 (рис. 8.2.3).
Рост s приводит в краткосрочном периоде к более быстрому росту, но лишь до тех пор, пока не установится новое состояние устойчивого равновесия.
На основании этих условий определяем равновесный рост исходя из категории Устойчивое состояние (Steady State): долгосрочное равновесие роста определяется как состояние, в котором в каждый момент времени рынки товаров и факторов производства находятся в равновесии и относительные экономические величины постоянны. С точки зрения инвестиций в условиях равновесия инвестиции равны выбытию sf (k) = 5к. Действует следующее условие:
K(t) =Y(t) - C(t) - 5K(t), т. е. I(t) = Sw. (10)
В Steady State величины на душу населения y(t), k(t), C(t) постоянны.
Далее для объяснения экономического роста вводится фактор роста населения (допущение 4). Дополнительный рост населения снижает равновесный уровень капиталовооруженности за счет распределения имеющегося запаса капитала между возросшим числом работников.
Темп роста производительности труда постоянен и задается экзогенно в виде n.
Если основной капитал растет с другим темпом, чем производительность труда, то изменяется:
- капиталовооруженность;
- для случая эластичности замещения о Ф 1 распределение дохода между факторами производства;
- темп роста производительности труда.
При этом экономика не находится в состоянии равновесия роста. Поскольку темп роста производительности труда экзогенен в модели, возникает вопрос, при каких условиях основной капитал растет с аналогичным темпом.
Темп роста населения задан экзогенно, как n, и постоянен. Однако определение темпа роста капитала отсутствует.
Инвестиции согласно определению представляют собой брутто-изменение основного капитала во времени, это означает K(t) = I(t) - 5K(t). Преобразуя, получаем фундаментальное уравнение движения:
y = f '(k)-[s f(k)/k - (n + 8)]-k. (11)
Отсюда в дальнейшем выводится долгосрочное равновесие. Оно существует для каждого k(t) 0, когда исполняется следующее условие:
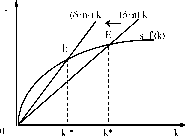
8.2.4).
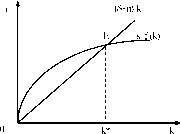
8.2.5). Отсюда следует вывод: страны с более высокими темпами роста населения имеют меньшую капиталовооруженность и, следовательно, более низкие доходы.
Отметим, что равновесие в модели Солоу характеризуется стабильностью. Возникает вопрос, способна ли экономика в любой выбранной точке отсчета k0, т. е. при любой относительной начальной оснащенности ресурсами, фактически достигнуть состояния равновесия. Это начальное значение капиталовооруженности может лежать как выше, так и ниже значения равновесия k*.
Ситуация характеризуется ненулевым доходом на душу населения.
Рассмотрим следующие ситуации.
1. k0 = k *. Фактические инвестиции на душу населения соответствуют инвестициям, которые требуются, чтобы при растущем населении основной капитал на душу населения оставался постоянным, s(y) = (n+5) k. Темпы роста обоих производственных факторов совпадают. Экономика находится непосредственно на своей равновесной траектории.
Модельно-эндогенные импульсы, являющиеся причиной, по которой экономика покинет состояние равновесия в данной ситуации, отсутствуют.
2. k0 k*. Ставка оплаты труда ниже, чем w*, и ставка дохода от капитала выше, чем равновесная ставка г*. Фактические инвестиции на душу населения sy превышают необходимые (n + 5)*k, что как раз обозначает то, что основной капитал растет с большим темпом, чем производительность труда, K L. Производственный фактор капитала относительно достаточен, фактор труда относительно ограничен.
Избыточное предложение капитала ведет к падению цены фактора капитала г, в то время как избыточный спрос на труд вызывает повышение ставки оплаты труда; w возрастает по отношению к w*, ставка дохода от капитала снижается относительно г*. Капиталоемкость возрастает до тех пор, пока темп роста капитала k* снижается до уровня темпа роста населения.
3. k(0) k*. Ставка оплаты труда выше, чем w*, норма прибыли (отдачи от капитала) ниже, чем г*. Фактические инвестиции на душу населения ниже, чем необходимые.
Производительность труда растет с большим темпом, чем основной капитал, L K. В этом случае капитал относительно ограничен, так что цена фактора г относительно г* возрастает, ставка оплаты труда w относительно w* снижается.
Капиталовооруженность сокращается до тех пор, пока темпы роста капитала k* автоматически не сравняются с темпом роста населения.
На основании полученных результатов можно сделать следующий вывод: цены факторов реагируют на относительную ограниченность факторов и приспосабливаются в каждый момент времени к изменяющимся рыночным условиям. Изменение капиталоемкости отражается в связи с непрерывно варьируемым введением в производство фактора капитала.
При экзогенно заданном темпе роста производительности труда n происходит приспособление в накоплении капитала. Это является следствием чрезмерного изначального основного капитала, при его недостаточности возникает противоположная ситуация.
В целом модель Солоу характеризуется следующими признаками:
(a) Долгосрочное равновесие роста существует, отчетливо и стабильно.
(b) Все макроэкономические агрегаты Y, K, L, C, S растут с одинаковым темпом n.
(c) Все величины на душу наседения y, k, c постоянны.
(d) Капиталовооруженность K/Y = k изменяется на траектории приспособления к равновесному росту вследствие субститу-циональной производственной технологии и конвергируется к равновесию роста с постоянной величиной.
(e) Равновесные цены в обоих рынках факторов w* и r* в Устойчивом состоянии постоянны.
(f) При постоянном соотношении вводимых факторов и постоянных ценах факторов равновесная траектория роста больше не изменяется, равно как и функциональное распределение доходов. Нормы доходов факторов капитала и труда постоянны.
(g) Изменение одного экзогенного структурного параметра экономики вызывает приспособление к новой равновесной траектории роста с изменившейся капиталоемкостью.
h) На оптимальной траектории роста норма сбережений соответствует норме прибыли. Потребление на душу населения максимизируется и остается с течением времени постоянным.
Этот результат свидетельствует также о том, что настоящие и будущие блага приносят одинаковую полезность.
Следующим этапом в развитии модели Солоу является ввод в нее фактора технического прогресса. У Солоу это величина экзогенно задана и для ее измерения вводится такой инструмент, как Солоу-резидиум (в ряде источников он обозначается как остаток Солоу).
Он охватывает ту часть темпа роста национального дохода, которая не может быть объяснена ростом производственных факторов труда и капитала. При определении Солоу-резидиума сначала упрощающе исходят из того, что производственные возможности экономики представлены функцией Кобба-Дугласа. Исходя из этого принимается, что технический прогресс Харрод-нейтрален и возникает вследствие роста эффективности труда А с постоянным темпом g:
Y = F (KM),
где LА - численность эффективных единиц труда.
Общее количество эффективных единиц труда LА растет с темпом n + g. С учетом этого уравнение изменения K во времени примет теперь вид:
Ak = i - k (5 + n + g)= s f(k) - k (5 + n + g) или s f(k) = k (5 + n + g).
Если определить к как количество капитала в расчете на единицу труда с постоянной эффективностью, т. е. k = K/LA, а yi = Y/LA, то рост эффективных единиц труда аналогичен росту числа занятых.
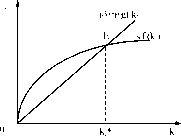
Следовательно, технический прогресс - единственное условие экономического роста, поскольку именно он обеспечивает рост ВВП на душу населения.
Наиболее существенные результаты анализа технического прогресса в модели Р. Солоу характеризуются следующими тезисами:
(a) При единой форме технического прогресса, который согласуется с концепцией равновесной траектории роста, речь идет о Харрод-нейтральном, т. е. чисто капиталосберегающем техническом прогрессе.
(b) При дополнительном допущении о постоянном распределении дохода линеарной гомогенной технологии Кобба-Дугласа три концепции нейтральности технического прогресса приводят к одинаковому результату.
(c) Интеграция автономного Хикс-нейтрального технического прогресса в модель Р. Солоу ведет к следующим результатам:
- на равновесной траектории роста измеряемые в единицах эффективности величины на душу населения kg, yg, cg постоянны;
- величины на душу населения (в эффективных единицах) к, y, c растут с экзогенным темпом технического прогресса g;
- агрегированные величины Y, K, C растут с суммой темпа роста населения и нормы технического прогресса, n + g;
- функциональное распределение дохода остается постоянным;
- реальная ставка оплаты труда растет с нормой технического прогресса.
Эмпирически вклад технического прогресса в рост ВНП определяется остаточным образом исходя из того, что нормы доходов, инвестиций и темп роста населения измеряются экспертным путем или с помощью статистических методов.
Детерминант роста в модели Солоу можно представить схематически следующим образом:
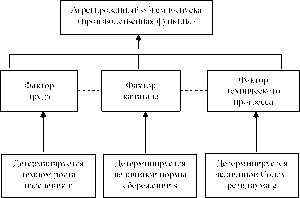
Причина этого заключается в необходимости подчеркивания задействования в процессе производства экономических благ, преобразование которых в средства производства и предметы потребления требует затрат как прошлого, так и живого труда. Также за рамки модели Солоу выносится влияние государства, которое может быть представлено в качестве институционального фактора роста.
Данная ситуация связана, на наш взгляд, с необходимостью обеспечения достаточной простоты и наглядности модели, а также вполне соответствует неоклассической традиции, нивелирующей роль государства в процессе производства.
Равновесный экономический рост совместим с различными нормами сбережения, но оптимальной будет только та, которая обеспечивает экономический рост с максимальным уровнем потребления. Оптимальная норма накопления соответствует золотому правилу, вошедшему в экономическую науку благодаря американскому экономисту Эдмунду Фелпс.
Э. Фелпс задался вопросом, какой величины капитал захочет иметь общество, находящееся на траектории сбалансированного роста. Если он будет достаточно большим, это гарантирует высокий уровень производства, но большая его часть пойдет не на потребление, а на накопление - общество не сможет насладиться плодами роста. Если же объем капитала будет слишком малым, то потреблять можно будет почти все, что произведено, но произведе-но-то будет совсем немного.
Где-то посредине между двумя крайностями, очевидно, находится оптимальная для общества точка, в которой достигается максимальный объем потребления.
Пусть k** - уровень капиталовооруженности, соответствующий норме накопления по Золотому правилу, а c** - уровень потребления.
Вся произведенная продукция расходуется на потребление и инвестиции:
у = c + i = c = y - i .
Подставив значения каждого из параметров, которые они принимали в устойчивом состоянии, получим:
c* = f(k*) - 5k*.
Отсюда определяется такой устойчивый уровень капиталовооруженности (k**), при котором максимизируется объем потребления (c**) и соответствует золотому правилу (рис. 8.3.1).
В точке Е производственная функция f(k*) и линия 5k* имеют одинаковый наклон и потребление достигает максимального уровня.
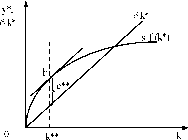
Поэтому технический прогресс является единственным фактором, обеспечивающим экономический рост в устойчивом состоянии, т. е. увеличение дохода на душу населения. Вместе с тем, каким образом он достигается, в модели Со-лоу не описывается, он является чем-то вроде манны небесной.
В завершение отметим, что в модели Солоу нахождение экономики той или иной страны на равновесной траектории роста определяется прежде всего экзогенно заданными величинами s, n и g. Экзогенный характер данных детерминант экономического роста обусловил критику модели Солоу и указал вектор развития современных теорий экономического роста в направлении эндоге-низации показателей темпа роста населения, уровня технического прогресса и нормы сбережений. Значительная часть современных так называемых теорий эндогенного роста посвящена рассмотрению данных аспектов проблемы и является одним из наиболее перспективных направлений экономической науки начиная с момента возникновения модели Солоу.