Расстояние между нечеткими множествами
Утверждение доказано.
Если мы имеем последовательность множеств
Аі С А2 G - - - Ап
и последовательность чисел
1 а1 а2 - - - ап 0,
то с помощью утверждения о декомпозиции мы можем синтезировать нечеткое множество А.
Функция принадлежности данного множества будет иметь следующий вид:
рл(и)
аі, если Нлі (и) = 1 и клі_1 (и) = 0 0, если клп (и) = 0,
где кл(и) - характеристическая функция множества А.
Это очень важное свойство, поскольку оно позволяет наряду с определением нечеткого множества как отображения рл(и) : U ^ [0,1] (с. 9) ввести понятие нечеткого множества как отображения рл(и) : 2и ^ [0,1]. В некоторых случаях последнее определение оказывается более удобным,
Расстояние между нечеткими множествами
Напомним определение расстояния.
Пусть V - некоторое множество, D+ множество неотрицательных действительных чисел и d : V х V ^ D+. Говорят, что d(x, у) - расстояние в V, если при x,y,z Е V выполнено
1) d(x, x) = 0
2) ф,у) = d(y,x)
3) d(x, z) d(x, у) + d(y, z).
Рассмотрим множество P(U). В нем можно ввести метрику, или расстояние между функциями принадлежности (нечеткими множествами).
Приведем примеры расстояний.
Пример 2 Можно привести следующие известные расстояния между нечеткими множествами:
- расстояние Хемминга для конечного универсального множества U : \U\ = и:
П
d(A, B) = ^ \Уа(ui) Цб(Ui)\;
i=1
- относительное расстояние Хемминга для конечного универсального множества U : \U\ = и:
Е
i=1
a(A,B)
\yA(ui) уБ (Ui)\,
- расстояние Хемминга для бесконечного универсального множества U С R1.-
d(A,B )= \yA(u) уБ (u)\du;
- относительное расстояние Хемминга для бесконечного универсального множества ^ R1;
- расстояние Евклида для конечного универсального множества U : \U\ = и:
e(A,B)
^2(yA(ui) уб (ui))2;
i=1
- относительное расстояние Евклида для конечного универсального множества U : \U\ = и:
П
e(A,B)
^2(yA(ui) Уб (ui))2;
i=1
- расстояние Евклида для бесконечного универсального множества U С R1.-
e(A,B)
- относительное расстояние Евклида для бесконечного универсального множества U С R1.-
Рис. 1.5:
Рис. 1.6:
Очевидно, что можно придумать и определить и другие расстояния. Выбор того или иного расстояния зависит от природы рассматриваемой проблемы. Каждое из них обладает своими преимуществами и недостатками, которые становятся очевидными в приложениях.
Понятие расстояния будет нами активно использовано ниже при определении степени нечеткости множества (раздел 1.5).
Измерение степени нечеткости множества
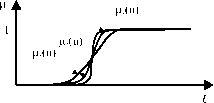
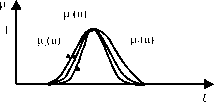
Нечеткие множества могут иметь разную степень нечеткости. Множества s и п типов, имеющих различную степень нечеткости, приведены на рис.
1.5 и рис. 1.6 соответственно (множество y^u) является наиболее ’’нечетким", множество y3(u) -наиболее ’’четким").
Меры нечеткости важны в приложениях теории нечетких множеств. Этот показатель является параметром оценки качества различных процедур и алгоритмов в распознавании образов, принятии решений, моделях поиска информации [40] - [43] и т.п.
Работы по измерению степени нечеткости начались с 1972 г. [68] Исторически первыми были разработаны методы оценки нечеткости через энтропию [21]; к настоящему времени можно выделить два основных подхода к оценке степени нечеткости множества: метрический и аксиоматический.
Оцека нечеткости через энтропию
Этот подход к оценке степени нечеткости множества базируется на использовании понятии энропии в физике. Степень неопределенности компонент физической системы относительно вероятности ее состояния составляет содержание понятия энтропии.
Поэтому желание использовать его для выичисления степени нечеткости (неопределенности) множества являлось естественным в силу очевидной аналогии. Напомним определение энтропии.
Пусть Пі, П2, - - - , Пп - состояния системы, p1,p2, ¦ ¦ ¦ ,Рп - вероятности состояний. Энтропия системы H(p1,p2, ¦ ¦ ¦ ,pn) определяется следующим выражением:
п H (pi,p2, ¦¦¦ ,pn) = -^2 pi Inpi (1.32)
i=1
Непосредственно из данного определения вытекают следующие свойства энтропии:
a) H = 0 (минимально), если
3j (1 j п) p = 1);
b) H = Inп (максимально), если yj (1 j n) (p2 = n).
Если в формуле ( 1.32) перед знаком суммы поставить нормировочный коэффициент іпП то значение энтропии будет меняться в пределах от 0 до 1.
Оценка степени нечеткости через энтропию заключается в следующем:
1) Проводится ’’нормировка" нечеткого множества A. Эта процедура выглядит следующим образом:
1.1) Вычисляется величина C(A) = рл (u)du в случае U С R1 или C(A) = ^2и-еи Рл(иі) для конечного универсального множества. Эта величина в разных работах называется ’’мощностью нечеткого множества", ’’массой нечеткого множества" и т. и.;
1.2) Строится нечеткое множество A следующим образом:
Рл (и) C(A) -
р л(и)
Множество A и есть ’’пронормированное" множество A.
2) В качестве степени нечеткости A берется значение пронормированной формулы ( 1.32) для пронормированного множества A:
С(А) = - 7-1- бА(иг) ln бА(иг) (L33)
in n
щ^и
Даже беглый анализ формулы ( 1.33) позволяет заметить, что значение степени нечеткости зависит не от собственно значений функции принадлежности, а от их отпоите, іыіых значений. Это приводит к следующим ’’парадоксам":
1) Степень нечеткости обычных множеств у$(и) ( 1.18) и уи(и) ( 1.21) максималь-
НсЦ
2) Минимальна только степень нечеткости множеств с единственным ненулевым элементом - как ’’четких", так и ’’нечетких".
Из сказанного вытекает, что энтропийная мера нечеткости обладает недостатками. Тем самым важны другие подходы к оценке степени нечеткости.
Метрический подход
Основная идея этого подхода к измерению степени нечеткости множеств базируется на использовании понятия расстояния между нечеткими множествами (раздел 1.4).
Идея метрического подхода заключается в оценке степени нечеткости как расстояния между оцениваемым множеством и некоторым множеством с известной степенью нечеткости.
Для строгого определения этой идеи нам понадобятся ряд понятий.
Пусть А - нечеткое множество. Обычное множество А с функцией принадлежности
{0, если ha(u) 0, 5
1, если ha(u) 0, 5
0 или 1, если ha(u) = 0,5
называется ближайшим к нечеткому множеству А.
Будем называть множество А* с известной степенью нечеткости базисным множеством.
Пример 3 В качестве примеров базисных множеств можно привести:
1) А* = А; Это множество определяется множеством А и им,ест степень нечеткости, равную нулю. Чем больше расстояние от некоторого множества до его ближайшего четкого множества, тем больше степень его нечеткости.
2) А* = А0,5, где уАоб (и) = 0.5 Чи Е U. Это максимально нечеткое множество. Чем ближе к нему некоторое нечеткое множество, тем больше степень его нечеткости.
Теперь мы можем дать определение степени нечеткости множества.
Пусть f - некоторая монотонная функция, р(х, у) - метрика в P(U), А* - базисное множество, тогда степенью нечеткости ДА) нечеткого множества А называется значение ДА) = f [р(А,А*)}.
Функция f подбирается для удовлетворения некоторым естественным требованиям для степени нечеткости, которые определяются для каждой задачи.
Примерами таких требований могут быть изменение степени нечеткости в пределах от 0 до 1, равенство степени нечеткости нулю для обычного множества и т.п. Подробнее о таких требованиях можно узнать в разделе 1.5.3.
Ниже приводятся примеры конкретных функционалов, измеряющих степень нечеткости.
Пример 4 В качестве примеров степени нечеткости можно привести:
1) ?і(А) = 2е(А,А); 0 ?і(Л) 1;
2) ?2(А) = 1 _ 2d(A, А0,5); 0 ?2(А) 1
Аксиоматический подход
Основная идея аксиоматического подхода заключается в формулировании некоторых ’’естественных" требований (аксиом) к степени нечеткости, и поиске конкретных функционалов, удовлетворяющих этим требованиям.
Обычно пользуются следующими аксиомами степени нечеткости множества.
P1. ? (А) = 0 (минимально) для ситуаци и, когда А - обычное множество;
P 2. ? (А0,5) = 1 (максимально);
P3. ? (А) ?(B), если рл(и) рв (и) при рв (и) 0.5 и рл (и) рв (и) при
рв (и) 0.5 (в этом случае говорят, что А является заострением B);
P4. ? (А) = ? (А) (симметриченость по отношению к 0, 5).
Иногда дабавляется аксиома P5.
P5. ? (А U B) + ? (А П B) = ?(А) + ?(B), т.е. ? является оценкой на решетке P (U).
Нетрудно проверить, что приведенные в примере 4 функционалы удовлетворяют данным аксиомам. И обратно, с помощью подбора функции f в рамках метрического подхода (определение 1.5.2) можно добиться удовлетворения P 1,P2; монотонность f и использование в качестве аргумента расстояния до обычного или максимально нечеткого множества гарантирует выполнение P3, P4.
Некоторые свойства степени нечеткости множества
Приведем некоторые свойства степени нечеткости, иллюстрирующие ее ’’естественность", то есть удовлетворение интуитивным представлениям о ней.
В качестве примера рассмотрим степень нечеткости ?(А) = 2е(А, А).
Рассмотрим множество нечетких множеств, имеющих одну и ту же степень нечеткости
Ф(А) = {B : ? (B) = ? (А)}. (1.34)
Равенство ?(B) = ? (А) явдяется условием отношения эквивалентности на P (U), Ф(А) - соответствующий класс эквивалентности.
Ниже формулируется ряд утверждений, часть из которых достаточно очевидна, часть доказана в работах [41], [43].
Утверждение 6 Соотношения B е Ф(А) м B Е Ф(А) эквивалентны,.
Пусть g - некоторая взаимнооднозначная функция, определенная на U. Нечеткие множество Лд, определяемое функцией принадлежности рЛд(и) = рЛ(д-1(и)) будем называть перестановкой множества Л.
Утверждение 7 Если Bg - перестановка множесгпва B, соотношения B Е Ф(Л) и Bg е Ф(Л) эквивалентны,.
Часным случаем перестановки является сдвиг функции принадлежности влево или вправо [41]. Поэтому справедливо
Следствие 1 Если B\ - сдвиг множесгпва B на \ единиц, соотношения B е Ф(Л) и B\ е Ф(Л) эквивалентны,.
Утверждение 8 Если для всех и из U выполнено ?Лі (и) Рл2 (и), то
1) ?(Лі) С(Л2) при ^Л2 о, 5;
2) С(Лі) С(Л2) при і^Лг о, 5.
Следствие 2 Если при i = 1, 2 выполнено Bi Е Ф(Л) и B3 = B1 П B2, то
1) ?(B3) ?(Л) при Цві(и) 0.5 У и Е U;
2) ?(B3) ?(Л) при pBi (и) 0.5 У и Е U.
Следствие 3 Если при i =1, 2 выполне но Bi Е Ф(Л) и B3 = B1 U B2, то
1) ?(B3) ?(Л) при pBi (и) 0.5 У и Е U;
2) ?(B3) ?(Л) при pBi (и) 0.5 У и Е U.
Последние два следствия свидетельствуют о том, что операция дополнения не выводит нас из класса функций одинаковой степени нечеткости; операции же пересечения и объединения, вообще говоря, не сохраняют класса функций одинаковой степени нечеткости. При последних двух операциях нечеткость может как увеличиваться, так и уменьшаться, однако кокой-либо систематический эффекит увеличения (уменьшения) нечеткости возможен при довольно сильных ограничениях, редко встречающихся на практике.
В заключении рассмотрим значение степени нечеткости для некоторых специальных типов функций принадлежности.
Справедливы следующие предложения.
Утверждение 9 Если рЛ(и) = s(u; a,@,Y), то ? (Л) = 3 (^ а).
Утверждение 10 Если рЛ(и) = п(и; (3,і), то ?(Л) = |
Содержательный смысл утверждений 9 и 10 состоит в том, что чем ’’круче" возрастает s функция и чем ’’уже" п функция, тем меньше их степень нечеткости.
Пусть функции принадлежности являются кусочно-линейными (Рис. 1.4). Обозначая через и^ и ив левую и правую границу области неопределенности, мы можем задать функцию принаждежности в аналитическом виде, а именно:
и uL uL и uR и uR
u uL Ul u UR u uR
Обозначим множество таких нечетких множеств через L. Справедливо следующее предложение.
Утверждение 11 Если A Е L, то ?{A) = -щщ, где d = uR uL.
Таким образом, чем меньше область неопределенности, тем меньше степень нечеткости множества, что согласуется с интуитивным представлениям о нечеткости, степени нечеткости множества, изложенными в 1.5.4.
Глава 2 Нечеткие отношения
Понятие отношения играет важную роль в математике и ее приложениях. Это понятие активно используется в теории автоматов [22]; распознавании образов [15]; при моделировании структуры сложных систем [23], [25], [27]; при анализе процессов принятия решений [23], [6] [28], [30] и многих других областях. Понятие отношения также можно обобщить на нечеткий случай. При этом обнаруживаются некоторые новые интересные свойства.
Так, например, понятие класса эквивалентности заменяется понятием подобия. Подобие является не таким жестким, и, поэтому, более подходящим для представления менее определенных и довольно часто встречающихся ситуаций.
В рамках нечетких отношений можно ввести некоторые новые типы отношений, например, сходства и несходства, более адекватно описывающих многие практические ситуации.
Нечеткие отношения вводятся как нечеткие подмножества специальным образом устроенного универсального множества. Многие понятия и свойства нечетких отношений в данной главе описаны схематично, поскольку подробный анализ их аналогов проведен в главе 1.
Основные операции и их свойства
Напомним определение прямого произведения двух множеств.
Пусть U1 = {ж} и U2 = {y} - обычные множества. Прямое произведение U1 х U2
множеств Ui и U2 есть множество упорядоченных пар вида (x,y), то есть
Ui х U2 = {(x,y) : x е Ui, y е U2}.
Пусть М - множество принадлежностей. Тогда нечеткое множество R такое, что
V(x,y) е Ui х U2 nn(x,y) еМ
называется нечетким бинарным отношением R в U1 х U2.
Можно привести следующий пример нечеткого бинарного отношения.
Пример 5 Пусть U1 = {x1,x2,x3}, U2 = {y1,y2,y3,y4,y5}, M = [0,1]. Тогда нечеткое бинарное отношение может бытъ задано следующей таблицей:
| R | Уі | V2 | ?з | V4 | V5 |
| xi | 0 | 0.3 | 0.5 | 0.9 | 0.3 |
| X2 | 0.7 | 0.2 | 1 | 0 | 0.1 |
| X3 | 0.9 | 0 | 1 | 0.7 | 0.4 |
Пусть Pn = Ui xU2 *¦- - - xUn - прямое произведение п множеств, M - множество принадлежностей. Нечетким п -арным отношением называется нечеткое множество в Pn, принимающее свои значения в M.
Ниже мы будем рассматривать только нечеткие бинарные отношения. Вводимые понятия естественным образом обобщаются на случай п арных отношений.
Для нечетких отношений вводятся понятия проекций следующим образом. Первая проекция нечеткого бинарного отношения R определяется функцией принадлежности
Дк (х) = тах Дп(х,у)-
у
Вторая проекция нечеткого бинарного отношения R определяется функцией принадлежности
?тгі?) = max Дп(х,?)-
X
Глобальной проекцией h(R) нечеткого бинарного отношения R называется вторая проекция первой проекции (или наоборот):
h(R) = maxmax дп(х,у) = тахтах дп (х,у).
X у у X
Понятия носителя, включения отношений и основные операции для них определяются аналогично соответствующим понятиям для множеств (раздел 1.2).
Носителем S(R) нечеткого отношения R называется обычное множество упорядоченных пар (х,?), для которых функция принадлежности положительна, то есть
S(R) = {(x,V): Дп(х,?) 0}-
Говорят, что нечеткое отношение L содержит нечеткое отношение R (R содержится в L), если для всех пар (х,у) из Ui х U2 выполнено цк(х,?) fiL(x,y)-
Говорят, что нечеткое отношение R является дополнением нечеткого отношения R, если для всех пар (х, ?) из Ui х U2 выполнено (х,?) = 1 цк.(х,?).
Говорят, что нечеткое отношение G является объединением нечетких отношений R и L (G = R U L), если для всех пар (х,?) из Ui х U2 выполнено Цд(х,?) = max [дп(х,?), цс(х,?)] -
Говорят, что нечеткое отношение G является пересечением нечетких отношений R и L (G = R П L), если для всех пар (х,?) из Ui х U2 выполнено дд(х,?) = mm[дn(x,?), д?(х,?)].
Говорят, что нечеткое отношение G является алгебраическим произведением нечетких отношений R и L (G = R - L), если для всех пар (х,?) из Ui х U2 выполнено Дд(х,?) = Дп(х,?) - Дс(х, ?)-
Говорят, что нечеткое отношение G является алгебраической суммой нечетких отношений R и L (G = R+L), если для всех пар (x,y) из U1 х U2 выполнено
Уд(x,y) = yn(x,y)+ Ус(х,?) - yn(x,y) ¦ yc(x,y)-
Говорят, что нечеткое отношение G является дизъюнктивной суммой нечетких отношений R и L (G = R®L), если для всех пар (x,y) из Ui х U2 выполнено G =(ППС) U (RUL).
Не трудно видеть, что, если мы заменим в определениях введенных операций функции принадлежности y(x, y) на характеристические функции h(x,y), то получим определения соответствующих операций, принятые в теории отношений. В этом смысле теория нечетких отношений является обобщением теории (обычных) отношений.
Так как нечеткие отношения есть нечеткие множества на специфическом универсальном множестве, основные операции над ними обладают теми же свойствами. Доказательства свойств аналогичны доказательствам, приведенным в 1.2.
Как и в случае нечетких множеств, нечеткое отношение можно декомпозировать на специальным образом устроенную систему обычных отношений и наоборот, из системы обычных отношений, удовлетворяющим некоторым требованиям, можно синтезировать нечеткое отношение. Такая декомпозиция и синтез нечетких отношений производится с помощью подмножеств а - уровня нечеткого отношения.
Пусть а Е [0,1], Re U х U. Подмножеством а - уровня нечеткого отношения R называется обычное подмножество Ra = {(x,y) : yR(x,y) а}
Функция принадлежности подмножества а - уровня задается выражением
RRa (x, y)
1, yn(x,y) а 0, yn(x,y) а
Достаточно очевидно, что, если а1 а2, то Rai С Ra2.
Утверждение 12 (о декомпозиции). Любое отношение R можно представить в форме
R = max а х Ra
a
Доказательство. Справедливы следующие соотношения:
yn(x,y)= max а = max а х уПа (x,y) = Утаха ахПа (x,y).
a^n(x,y) a
Утверждение доказано.
| 0.9 |
|
| 1 - |
|
Композиция нечетких отношений
Операция композиции нечетких отношений Ri в X х Y и R2 в Y х Z позволяет определить нечеткое отношение в X х Z.
(Max-min) - композиция и ее свойства
Пусть Ri есть нечеткое отношение в X х Y, R2 - нечеткое отношение в Y х Z. (Max-min) - композиция Ri о R2 определяется выражением
Цщощ(x,z) = max [minj^R(x,y),^n2(y,z)}] , (2.1)
y
где x E X, y e Y, z E Z.
Вычисление композиции нечетких отношений аналогично вычислению произведения матриц, (’’столбец на строку"), только вместо произведения и суммы выполняются операции взятия минимума и максимума соответственно.
Пример б
| 0.2 - |
|
| 0.2 | 0.5 | 0 | 1 |
| 04 | 0.3 | 0.9 | 0 |
| 1 | 0 | 0.7 | 0.5 |
| 0.4- |
|
| 0.3 - |
|
| , 0.7 - |
|
| 0.5 |
|
Пример 7 Пусть X = {хьХ2,Хз}, Y = {уі,у2,Уз,Уі,Уъ}, Z = {zb Z2, Z3, Z4}. шение Ri на X х Y задано следующей матрицей:
| Ri | Уі | У2 | Уз | У 4 | У5 |
| xi | 0.1 | 0.2 | 0.5 | 0.7 | 0.3 |
| Х2 | 0.3 | 0 | 1 | 0.3 | 0.7 |
| Хз | 0.1 | 0.8 | 0 | 0 | 1 |
| Нечеткое | отношение R2 | на Y | |||
| R2 | zi | z2 | Zз | z4 | |
| Уі | 0.9 | 0 | 0.4 | 0.7 | |
| У2 | 0.3 | О.4 | 0.9 | 1 | |
| Уз | 1 | О.4 | 0.2 | 0 | |
| У 4 | 0.3 | О.4 | 0.7 | 0.2 | |
| Уз | 0.5 | 0.5 | 0.9 | 0.1 |
Тогда нечеткое отншение Ri о R2определено на X х Z и имеет выражается следующей матрицей:
| R2 | zi | z2 | z3 | z4 |
| xi | 0.5 | O.4 | 0.7 | 0.2 |
| x2 | 1 | 0.5 | 0.7 | 0.8 |
| x3 | 0.5 | 0.5 | 0.9 | 0.8 |
- ассоциативность: (R3 о R2) ? Ri = R3 ? (R2 ? Ri);
- дистрибутивность относительно объединения:
Ri о (R2 U R3) = (Ri о R2) U (Ri о R3);
- не дистрибутивность относительно пересечения:
R3 о (R2 П Ri) = (R3 о R2) П (R3 о Ri);
монотонность:
A^B ^Яо Л^ЯоБ.
Доказательства данных свойств достаточно очевидны. Читателю предлагается их провести самостоятельно по схемам, которые были нами применены в 1.2. (Мах-х) - композиции
Понятие (Max-min) - композиции можно обобщить следующим образом: заменить в ( 2.1) операцию min на любую другую, для которой выполняются свойство ассоциативности и монотонного неубывания по каждому аргументу:
Пусть операция х является ассоциативной и монотонно не убывает по каждому аргументу. (Мах-х) - композиция определяется следующей функцией принадлежности
Тпі*П2 (x, z) = max [рПі (x, y) х уП2 (y, z)} , (2.2)
y
где x E X, y e Y, z E Z.
Важным частным случаем (Мах-х) - композиции является (Мах--) - композиция. В этом случае операция "х" - это произведение, и, таким образом, ( 2.2) принимает
СЛ?ДуЮЩИИ ВИД!
^Ri-R.2 (x, z) max [^Ri (x, y) * ^R.2 (y, z)} ,
У
где x E X, y E Y, z E Z.
Другим примером (Мах-х) - композиции в случае, когда множество принадлежностей M = [0,1], является композиция, получаемая из ( 2.1) заменой операции min на среднее арифметическое:
TRi-R2 (x z)
(Tni (x,y) + Тп2 (y,z))
max
y
где x Е X, y Е Y, z E Z.
Другие конкретные (Max-*) - композиции и их свойства рассматриваются в работах [21], [29].
Выбор того или иного варианта (max-*) - композиции в приложениях определяется свойствами задачи.
Нечеткие бинарные отношения в U х U
Рассмотрим случай U1 = U2 = U, M = [0,1]. Для нечетких отношений довольно естественно вводятся свойства рефлексивности, симметричности и транзитивности.
Нечеткое бинарное отношение R называется рефлексивным, если yR(x,x) = 1 Ух Е U.
Нечеткое бинарное отношение R называется симметричным, если yR(x,y) = а ^ Уя(y,x) = а yx,y Е U.
Нечеткое бинарное отношение R называется транзитивным, если yR(x,z) maxy [yn(x,y),yn(y,z)] yx,y,z E U.
Пример 8 Отношение "x близко к у" рефлексивно, симметрично, но не транзитив-но; отношения "у много больше х" "у чище х" - не рефлексивны, не симметричны, но транзитивны.
Транзитивное замыкание нечеткого бинарного отношения
Пусть R - нечеткое отноше ние в U х U. Определ им R2 = RoR функцией принадлежности
Уя2 (x,z) = max[min(pn(x,y),pn(y,z))], y
где x,y,z Е U.
Сравнивая последнее выражение с определением транзитивности для нечетких бинарных отношений, не трудно увидеть, что свойство транзитивности можно записать в следующем виде:
R2 CR
Аналогично можно определить по индукции Rk\
Rk = RoRk-1, k = 2, 3,....
Пусть R2 C R и Rk+1 C Rk, k = 2, 3,.... Тогда, очеви дно, Rk С R.
Транзитивным замыканием нечеткого бинарного отношения будем называть отношение
(2.3)
к = ки 7г2 и я3 и....
Справедливо следующее
Утверждение 13 Транзитивное замыкание любого бинарного отношения есть транзитивное бинарное отношение
Доказательство. Согласно ( 2.3) можно записать:
п2 = пок = п2 ип3 ип4 и....
Сравнивая последнее выражение с ( 2.3), можно записать: П2 С П, что и доказывает транзитивность П.
Утверждение доказано.
Как проверить, построили мы или нет транзитивное замыкание конкретного нечеткого бинарного отношения? Ответ на этот вопрос дает следующее
Утверждение 14 Пусть П - некоторое нечеткое бинарное отношение. Если существует к такое, что Пк+1 = Пк, тоП = ПиП2 U ... иПк.
Доказательство. Доказательство непосредственно следует из соотношений:
п = пиП2 и... ипк ипк+1 ипк+2 и... =
= пип2 и... ипк ипк ипк и... = пип2 и... ипк.
Утверждение доказано.
Всегда ли композиция пі оп2 ил и п2 опі двух транзитивных отн ошений пі и п2 есть транзитивное отношение? Можно привести пример, что это свойство не всегда выполняется.
Пример 9 Пусть пі задается таблицей ( 2.4)- Это отношение транзитивно, т.к.
