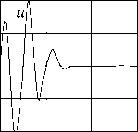
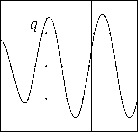
Законы управления и законы динамики физических систем

Причина появления отраженной волны колебаний видится в асимметрии уравнений (7.28): сила упругости, действующая на крайние маятники, отличается от силы, действующей на внутренние маятники.
Обратимся теперь к системе из циклически соединенных маятников. Отсутствие краевых эффектов в этой системе демонстрируется рис. 7.8, который получен в условиях, совпадающих с условиями получения рис.

7.7, но для системы (7.30).
На рис. 7.9, 7.10 показаны некоторые результаты применения алгоритма (7.34) к системе (7.30). Приняты значения у = 0.8, а = 0.7.

Как видно из графиков, при циклическом соединении маятников поставленная комбинированная цель управления достигается.

Рис. 7.6.

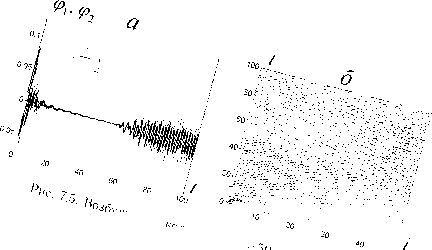
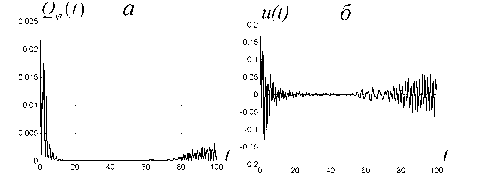
Целевая функция Q^ и сигнал управления. N = 50, а = 1.

Рис. 7.7.

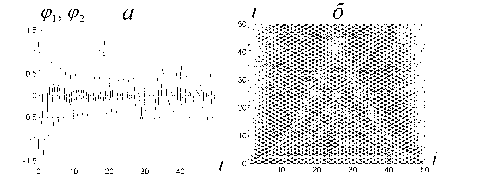
Свободные колебания. N = 50, и(Т) = 0.

Рис. 7.8. Свободные колебания при циклическом соединении маятников.

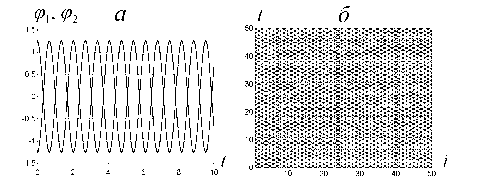
N = 50.

Рис. 7.9.

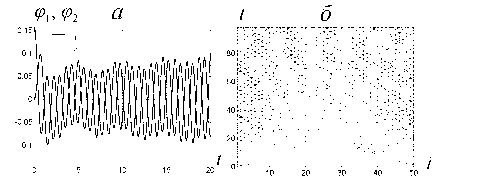
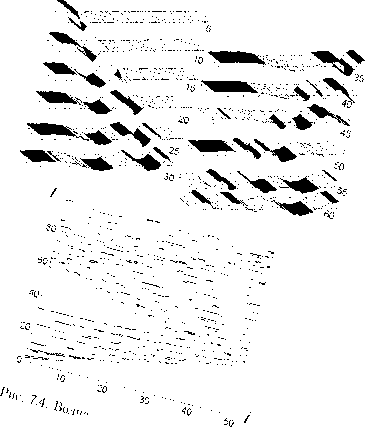
Возбуждение колебаний при циклическом соединении маятников.

Рис. 7.10.

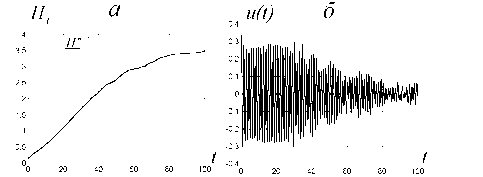
Полная энергия и управление при циклическом соединении маятников.

Законы управления и законы динамики физических систем

В настоящей главе исследуются связи между законами управления в технических системах и законами динамики физических систем. Показывается, что методы синтеза алгоритмов управления позволяют выводить законы динамики физических систем.

В частности, модели динамики ряда физических систем могут быть выведены на основе метода скоростного градиента при соответствующем выборе целевой функции. Изложение в основном следует [80, 134].

Вариационные принципы. Принцип скоростного градиента

Рассмотрим класс открытых физических систем, модели динамики которых описываются системами дифференциальных уравнений
X = f (x, и, t), (8.1)
где x e Rn вектор состояния системы, и вектор входных (свободных) переменных, t 0. Задача моделирования (построения модели) системы может быть поставлена как нахождение закона изменения (эволюции) и(Т), удовлетворяющего некоторому критерию естественности ее поведения и придающего создаваемой модели свойства, наблюдаемые у реальной физической системы.
В физике подобные постановки хорошо известны. Давно получили признание вариационные принципы построения моделей систем. Вариационный принцип обычно предполагает задание некоторого интегрального функционала (например, функционал действия в принципе наименьшего действия [47, 49]), характеризующего поведение системы.

Минимизация функционала определяет реально возможные траектории системы {х(Т), и(Т)} как точки в соответствующем функциональном пространстве. Для явного определения закона динамики системы используется развитый аппарат вариационного исчисления.
Интересно, что вариационный подход лег в основу целого направления в теории управления: теории оптимального управления, в которой минимизация функционала используется для нахождения подходящего в заданном смысле закона управления технической системой. В свою очередь, методы оптимального управления (динамическое программирование Беллмана, принцип максимума Понтрягина и др.), являющиеся развитием методов классического вариационного исчисления, могут быть применены к построению моделей динамики механических [13], термодинамических [58] и других систем в природе и обществе.
Кроме интегральных были предложены и дифференциальные (локальные по времени) принципы, такие как принцип наименьшего принуждения Гаусса, принцип минимальной диссипации энергии и др. Как отмечал М. Планк [67], локальные принципы имеют некоторое преимущество перед интегральными, поскольку они не ставят в зависимость текущее состояние и движение системы от ее позднейших состояний и движений.

Следуя [80], сформулируем еще один локальный вариационный принцип, основанный на методе скоростного градиента.
Принцип скоростного градиента: среди всех возможных движений в системе реализуются лишь те, для которых входные переменные изменяются пропорционально скоростному градиенту от некоторого целевого функционала Q_t.
Принцип скоростного градиента предлагает исследователю на выбор два типа моделей динамики систем: А) модели, следующие из алгоритмов скоростного градиента в дифференциальной форме
U = rV_uQ_t; (8.2)
В) модели, следующие из алгоритмов скоростного градиента в конечной форме
и = -rv_uQ_t. (8.3)
Здесь Q_t скорость изменения целевого функционала вдоль траектории системы (8.1). Опишем схему применения принципа в простейшем (но и важнейшем) случае, когда класс моделей динамики (8.1) задан соотношением
и = и. (8.4)
Соотношение (8.4) означает всего лишь, что мы ищем закон изменения скоростей переменных состояния системы. В соответствии с принципом скоростного градиента прежде всего нужно ввести целевой функционал (функцию) Q(x).

Выбор Q(х) должен быть основан на физике реальной системы и отражать наличие в ней тенденции к уменьшению текущего значения Q(х(Т)). После этого закон динамики может быть немедленно выписан в виде (8.2) или (8.3).
При этом задание закона динамики в виде (8.2) порождает дифференциальные уравнения движения второго порядка, которые инвариантны относительно замены времени t на (-t), т. е. соответствуют обратимым процессам. Напротив, выбор конечной формы (8.3) соответствует, как правило, необратимым процессам.
В следующем параграфе введенный принцип будет проиллюстрирован примерами.

Примеры скоростно-градиентных законов динамики

Пример 8.1. Движение материальной точки в потенциальном поле.

В качестве первого примера рассмотрим задачу описания движения материальной точки в потенциальном поле. Переменными состояния здесь являются координаты точки, т. е. х = col{xi, х₂, х₃}.

Выберем в качестве целевой функции потенциал поля Q(х) и выведем скоростно-градиентный закон движения в дифференциальной форме. Вычислим скоростной градиент:
Q = ^Q(х)]т и, V_UQ = VxQ(х).
Выбирая диагональную положительно-определенную матрицу Г в виде Г = т-11₃, где m 0 параметр, І₃ единичная 3 х 3 матрица, приходим к классическому закону динамики Ньютона: U = m-1VQ(х), или
mx = VQ (х). (8.5)
При этом параметр т интерпретируется как масса точки. ?
Пример допускает далеко идущие обобщения. Для систем, движущихся под действием потенциальных сил потенциал поля может играть роль целевой функции QM, а матрица инерции определяет матрицу коэффициентов усиления в алгоритме.

При этом если инерционные свойства системы различны в различных точках конфигурационного пространства, то метрика в пространстве скоростей (управляющих переменных) будет переменной. Таким образом можно строить модели динамики сложных механических систем, описываемых уравнениями Лагранжа 2-го рода.
Принцип скоростного градиента применим и к построению моделей динамики распределенных систем, описываемых в бесконечномерных пространствах состояний. В частности, х может быть вектором гильбертова пространства X, а f (х, и, Т) нелинейным оператором, определенным на плотном множестве D_F с X (при этом решения уравнения (8.1) понимаются как обобщенные решения).
Пример 8.2. Волновое уравнение и уравнение теплопроводности.

Пусть х = х(г), г = со1(г₁, г₂, г₃) е О поле температур или концентраций вещества, определенное в некоторой области О с R3. Выберем в качестве целевого функционала меру неоднородности поля:
Qt(x) = \ f |?_гх(гЛ)|2 dr, (8.6)
О
где ?_гх(г, t) пространственный градиент поля х = х(г). Полагая для простоты граничные условия нулевыми, вычислим скоростной градиент функционала (8.6). Из формулы Грина с учетом нулевых граничных условий имеем
Q_t = (?_гх(г, Т))т?_ги(г, t) Dr = Ax (г, T)u(r, t) Dr, (8.7)
ОО
3 ₂
где A = ^2 - оператор Лапласа. Учитывая, что градиент от ска-
І = 1
лярного произведения по одному сомножителю равен другому сомножителю, , получаем, что оператор скоростного градиента в данном случае не что иное как оператор Лапласа: V_uQ_t = Ах (г, Т). Следовательно, скоростно-градиентный закон эволюции системы в дифференциальной форме (8.2) примет вид
^-_x(r,t) = 7 Ах (г, t), (8.8)
что соответствует волновому уравнению. Если же выбрать алгоритм в конечной форме (8.3), то уравнение динамики примет вид
дх
(t) = ₁Ax(rJ), (8.9)
что совпадает с простейшим уравнением теплопроводности, описывающим процессы теплопередачи и диффузии. ?
Пример 8.3. Динамика вязкой жидкости.

Пусть бесконечномерный вектор состояния системы образован из двух функций: х = со1(?(-, t),р(-, t)), где v(r, t) е R3 поле скоростей трехмерного течения жидкости, р(г, t) поле давлений. Введем целевой функционал следующим образом
(8.10)
Qt = р(г, t) dr + vo \VrV(r, t)\2 dr,
где v₀ 0 весовой коэффициент. Вычисление скоростного градиента функционала (8.10) по отношению к (8.4) дает V_uQ_t = V_гр v₀А?. Поэтому дифференциальная форма закона скоростного градиента не что иное как уравнение Навье-Стокса, описывающее движение вязкой жидкости:
д?
P^-(r, t) = -?_гр(г, t) + іу₀А?(г, t), (8.11)
dt
где v = v₀7-1 коэффициент вязкости, p = 7-1 - плотность жидкости. ?
Другие примеры вывода уравнений динамики механических, электрических и других систем можно найти в [80]. Принцип скоростного градиента применим к описанию широкого класса физических систем, находящихся под действием потенциальных или диссипативных сил. С другой стороны, к системам, совершающим вихревые
движения, например, к механическим системам, находящимся под действием гироскопических сил, принцип скоростного градиента, по-видимому, не применим.
Еще раз подчеркнем, что принцип носит двойственный характер: дифференциальная форма закона скоростного градиента соответствует обратимым, тогда как конечная форма необратимым процессам. Выбор между ними, так же как и выбор цели и целевого функционала целиком лежит в области физики. В каких-то случаях этот выбор не однозначен: например, процесс, обратимый на одних масштабах времени может быть необратимым не других масштабах.

Таким образом, принцип не решает за физика вопрос о построении модели системы, а лишь помогает сузить множество вариантов при принятии решения и выявить целенаправленность в поведении системы.

Соотношения Онсагера

Принцип скоростного градиента позволяет по-новому взглянуть на некоторые известные физические факты и явления. Выведем, например, обобщенный вариант известного принципа симметрии кинетических коэффициентов (принцип Онсагера) в термодинамике [48, 65, 188].

Рассмотрим изолированную физическую систему, состояние которой характеризуется набором термодинамических переменных ?_ь?₂, . ..,?_п.

Обозначим через х_і = отклонения переменных от своих равновесных значений ?П, Q,..., С_п. Пусть динамика величин х₁,х₂,... ,х_п описывается дифференциальными уравнениями
Хі = Ui(хі,Х2,...,Хп), і = 1,2, ...,n. (8.12)
Линеаризуем уравнения (8.12) вблизи равновесия:
п
Хі = ^ \ikXk, і = 1, 2,..., п. (8.13)
К=1
Принцип Онсагера [24, 65, 188] состоит в том, что величины \_ik(так называемые кинетические коэффициенты) удовлетворяют соотношениям симметрии
Xik Xki, l,k І,2,...,п.
157
Принцип Онсагера верен не для всех систем. Существующие его доказательства (см., напр., [48]) опираются на дополнительные постулаты.

Ниже дается новое доказательство, которое показывает, что для скоростно-градиентных систем обобщенный вариант принципа Онсагера верен без дополнительных предположений и не требует предварительной линеаризации модели системы.
Прежде всего необходимо сформулировать этот вариант. Легко видеть, что для линейной модели системы (8.13) соотношения (8.14) равносильны следующим тождествам:
дщ
дх_к
дщ
дхі
(Хі, Х2, ...,Х_п)
(Хі, X2, . . . ,Xn).
(8.15)
Будем называть обобщенным принципом Онсагера выполнение соотношений (8.15) для систем, описываемых нелинейными уравнениями (8.12).
Теорема 8.1. Предположим, что существует гладкая функция Q(х) такая, что уравнения динамики системы (8.12) получаются по принципу скоростного градиента в конечной форме при целевой функции Q(х).
Тогда для всех х₁,х₂,...,х_п справедливы тождества (8.15), т. е. обобщенный принцип Онсагера.
Доказательство теоремы 8.1. Доказательство весьма простое. Поскольку (8.12) есть закон скоростного градиента для Q(x), правые части могут быть представлены в форме
dQ дщ ’
і = 1, 2,..., п.
Щ = -у
Следовательно, щ = y(dQ/дхі) (в силу Q = (?^)Ти) и
дщ d2Q дщ
dx_k ^ дхДx_k дхі ’
что влечет справедливость тождеств (8.15). ¦
Очевидно, соотношения (8.14) являются частным случаем (8.15) для линейных уравнений динамики. Таким образом, для систем, подчиняющихся принципу скоростного градиента обобщенные соотношения Онсагера (8.15) справедливы без предположения о линейности уравнений динамики, т. е. не только вблизи равновесия.
Замечание 8.1. Приведенный выше вывод справедлив в предположении гладкости правых частей (8.12), поскольку основан на дифференцировании.

На первый взгляд, это исключает из рассмотрения задачи с негладкими и разрывными функциями, например, задачи о движении ударных волн. Однако в этих случаях можно использовать варианты алгоритмов скоростного градиента, специально разработанные для негладких задач, в которых градиент уступает место субградиенту [80].

Динамика и цель

Интересно сравнить описанный выше подход с результатами известного английского специалиста в области кибернетики Г. Ро-зенброка [213, 214], который продемонстрировал вывод основных уравнений квантовой механики на основе принципов оптимального управления. В [213, 214] показано, что уравнение Шредингера оказывается непосредственным следствием принципа оптимальности Гамильтона-Якоби-Беллмана.
Хотя подход к построению уравнений динамики физических систем на основе экстремальных принципов хорошо известен, он обычно не увязывается в физике с понятием цели, поставленной как достижение экстремума целевого функционала. В этом проявляется различие подходов в физике и инженерных науках, где оптимальность как цель создания искусственной (технической) системы обычно ставится во главу угла.

В физике же и в других естественных науках использование понятий цели и целесообразности поведения системы, наоборот, подвергалось сомнению рядом ученых. Наиболее ярко такие взгляды выразил А. Эйнштейн [121]:
... Для ученого есть только "существующее", но нет желающего, нет оценивающего, нет добра, нет зла, нет цели.
Г. Розенброк критикует позицию А. Эйнштейна, приводя аргументы в пользу того, что понятие цели естественно как для живой, так и для неживой природы. Он отмечает, что неприятие дели является реакцией на конфликт XVII столетия между церковью и зарождающейся наукой и на сегодняшний день не является актуальной. В XX XXI столетиях машины, действующие целенаправленно и воплощающие дели, заложенные в них человеком, распространились повсеместно и уже стали частью окружающей нас среды!

Это заставляет придавать более серьезное значение понятию дели и в физике как науке о наиболее общих закономерностях систем окружающей среды: живых, неживых и искусственных, созданных человеком. Г. Розенброк пишет:
... Живые организмы, очевидно, имеют свои дели, и, если субстрат квантово-механических частиц, из которых состоит все живое, описываются как не имеющий целей, то возникает вопрос: как может дель возникнуть из бесцельного субстрата?
Описанный выше локальный принцип эволюции на основе скоростного градиента опирается на понятие дели еще в большей степени, чем интегральные экстремальные принципы. Поэтому в тех случаях, когда понятия дели и целевой функции возникают естественным образом, он может оказаться более удобным и полезным для построения моделей динамики систем.

Кстати, принцип скоростного градиента согласуется и с известным биологическим принципом, по которому организмы и популяции развиваются так, чтобы обеспечить максимальный прирост своей биомассы [73, 80].

ПРИМЕРЫ

Управляемый маятник Капицы

В 1940-х годах академик, впоследствии лауреат Нобелевской премии по физике П.Л. Капица провел эксперимент, демонстрирующий, что верхнее, неустойчивое положение равновесия маятника становится устойчивым, если ось подвеса маятника вибрирует в вертикальном направлении с достаточно большой частотой [38] (см. также [14, 15]). Этот эксперимент был объяснен П.Л.Капицей на основе введения так называемого эффективного потенциала, что соответствует варианту метода усреднения.

Работа П.Л.Капицы дала толчок к развитию нового раздела механики вибрационной механики [14, 15]. Аналогичные идеи легли и в основу соответствующего раздела теории управления: вибрационного управления [95, 181].
Математическая модель маятника Капицы имеет вид (рис. 9.1)
Jф + дф + mgl sin ф = mlu sin ф, (9.1)
где ф = ф(Т) угол отклонения маятника от нижнего вертикального положения; и = и(Т) вертикальное ускорение оси подвеса, являющееся управляющим воздействием; J = ml2 момент инерции маятника; д 0 коэффициент трения. П.Л. Капица рассматривал гармонический закон перемещения оси подвеса с частотой и и амплитудой А, при котором и(Т) имеет вид
u(T) = Au2sin ut, (9.2)
и экспериментально обнаружил эффект стабилизации маятника вблизи верхнего, неустойчивого равновесия. Многочисленные теоретические исследования (проводившиеся как до, так и после экспериментов П.Л. Капицы) [15, 226] показывают, что стабилизация неустойчивого равновесия наступает при достаточно большом и, т.е. если входное воздействие в (9.1) достаточно велико [15, 38, 51] (точнее, при выполнении условия Аио /цу где cjo = л/l^g/O ~ частота малых колебаний маятника вблизи нижнего положения равновесия).

При этом перемещение точки подвеса может оставаться малым, что усиливает парадоксальность эффекта. Таким образом, стабилизация
неустойчивого равновесия высокочастотным гармоническим воздействием возможна. При этом, однако, требуется приложение значительных сил.

и -0.1 і=0.025

Рис. 9.2. Распределение угла отклонения маятника (9.1)
с управлением (9.2) при J = 1, д = 0.025, т = 1,I = 1м, у = 0.1.
Поставим вопрос: можно ли добиться аналогичного поведения маятника Капицы при меньшей амплитуде и(Т), если в законе вибрации оси подвеса используется обратная связь?
Традиционный для теории автоматического управления подход, основанный на линеаризации модели объекта, в данном случае не проходит. Действительно, линеаризация дает хорошее приближение лишь вблизи положения равновесия или некоторой траектории, а нас интересует глобальное решение, работающее во всем пространстве состояний маятника.
Поставим вспомогательную цель управления:
lim Н(t) = Н*, (9.3)
где
H = ^(Ф)2 + mgl( 1 - cos (p) (9.4)
- полная энергия маятника. Цель (9.3) несколько отличается от традиционных для теории управления целей регулирования и слежения.

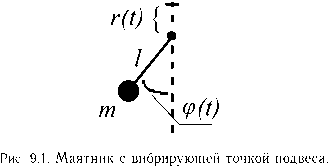
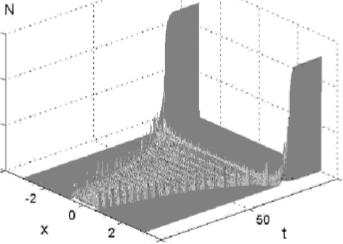
Скорее, она выглядит как цель человека, раскачивающегося на качелях. Аналогичная задача может возникнуть при запуске вибрационной установки, проектирования шагающего робота, в маятниковых часах и т. д.
Здравый смысл подсказывает, что раскачивание требует значительно меньше усилий, чем удержание маятника (или руки робота) в некоторой фиксированной позиции. Можно ли раскачать качели до верхнего положения маломощным воздействием?
Обратимся к методу скоростного градиента, задав в качестве целевой функции величину Q = (Н Н*)2/2 отклонение полной энергии маятника от желаемого значения Н*. Вычисляя скорость изменения функции Q вдоль траекторий системы (9.1) с фиксированным и, а затем градиент (в данном случае частную производную) от скорости по управлению, приходим к простым алгоритмам:
и = у(Н Н* )?sin ^, (9.5)
и = y sign [(Н Н*)ф sin ^] . (9.6)
Остановимся на алгоритме (9.6) и выберем в качестве желаемого уровня энергии энергию маятника в верхнем равновесии: Н* = 2mgl. Тогда из теоремы 4.2 (см. пример 4.1) следует, что в системе (9.1), (9.6) достигается уровень энергии не меньший, чем
(9.7)
и, следовательно, уровень И* = 2mgl будет обеспечен при 7 2qu₀(рис. 9.2).

В частности, при q = 0 стабилизация поверхности уровня энергии И = И* достигается при сколь угодно малой амплитуде управления 7. При малом демпфировании q амплитуда управления 7 также может быть выбрана малой.
Достижение требуемого уровня энергии еще не означает стабилизации равновесия, лежащего на этом уровне. Однако в работах [83, 221, 222] показано, что если q = 0, то несколько модифицированный алгоритм (9.6) при И* = 2mgl обеспечивает сходимость И(p(t), ф(і)) ^ И* и сходимость (p(t), (p(t)) (п,0) при t при
любых начальных условиях. При этом величина 7 0 может быть сколь угодно малой.
Задача об управлении маятником путем перемещения точки подвеса имеет интересную особенность. Поскольку управляющим воздействием u(t) является ускорение, из общих свойств алгоритмов скоростного градиента следует, что и(Т) ^ 0 при t -^ж. Однако при этом остается неясным, что будет происходить со скоростью и положением точки подвеса.

Формальная модель допускает, что скорость и отклонение положения точки подвеса от начального не стремятся к нулю и могут даже неограниченно возрастать, что лишает решение практической значимости.
Опишем, следуя [83], модификацию алгоритмов управления, свободную от указанного недостатка. Для этого введем расширенную целевую функцию 2і = Q + 7jZTPz, (9.8)
где г = co1(Z, Z), Р = Рт Д 0 - положительно полуопределенная весовая матрица и Z, Z - соответственно, высота и скорость точки подвеса. Тогда соотношение Z = и можно рассматривать как дополнительное уравнение движения, т. е. система превращается в систему с двумя степенями свободы и состоянием х = co1(q, QZ, Z).
В соответствии с методом скоростного градиента вычислим
0і
Q + гт Р
+ гтР
(9.9)
и,
где VuQi = (Н0 - И*)Q sin q + Р22Z + P12Z, P11, P22 - элементы второго
164

t, Рис. 9.3. Моделирование маятника с алгоритмом (9.10) при ц = 2 и ? = 0.
столбца матрицы Р. Модифицированный алгоритм управления задается выражением
и = -д(#0 - И*)gsin q - - ?(, (9.10)
где у 0, i 0, ? 0 - коэффициенты усиления.
Результаты гл. 3 для исследования полученной системы не применимы, поскольку исходная система не является гамильтоновой. Тем не менее, используя более общие результаты [61, 82], можно показать, что новая цель управления достигается и Z(Т) ^ const для почти всех начальных условий при ? = 0. Результаты моделирования с законом управления (9.10) и т = 1,1 = 1, y = 0.7, i = 2, ? = 0 представлены на рис.

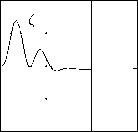
9.3.
Если же i 0, ? 0 то в системе обеспечивается более сильное свойство Z(Т) ^ 0, т. е., отклонение точки подвеса от начального положения асимптотически исчезает. Этот факт иллюстрируется результатами моделирования рис.

9.4, где ? = 2, а остальные параметры те же, что и в предыдущем случае.
Аналогичным образом может быть получен алгоритм раскачки

Рис. 9.4. Моделирование маятника с алгоритмом (9.10) при ц = 2 и ? = 2.
и для случая, когда точка подвеса перемещается горизонтально или наклонно. Дополнительные трудности могут возникнуть из-за неполноты или неточности измерений, например, если недоступна измерению угловая скорость р(Т). Может помешать неполнота управления, например, когда нельзя пренебречь инерционностью двигателя, вращающего маятник, и динамика управляемой системы описывается уравнениями
Jp + mgl sin р = mlu sin p, TU + и = v, (9.11)
где v = v(T) новый сигнал управления.

Содержание раздела