Задача о выбросе из потенциальной ямы

Действительно, управляющее воздействие ?(Т) не входит в правую часть первого уравнения
(9.11) и скоростной градиент оказывается равным нулю.
Современная теория нелинейного и адаптивного управления предлагает широкий арсенал подходов к преодолению указанных трудностей [6, 61, 75].

Задача о выбросе из потенциальной ямы

Задача о выбросе из потенциальной ямы (или о преодолении потенциального барьера) под воздействием внешних сил встречается во многих областях физики и механики [35, 230]. Иногда выброс явление нежелательное (прощелкивание мембран и оболочек, опрокидывание судов или экипажей), в других случаях выброс необходим.

Часто переход через потенциальный барьер соответствует фазовому переходу в физической системе. Во всех случаях нужны условия, гарантирующие наличие перехода через барьер или его отсутствие. Обычно исследуется случай типового гармонического внешнего воздействия [35, 230].

При этом представляет интерес, насколько мала может быть амплитуда воздействия, вызывающая выброс.
Во многих работах явление исследуется для нелинейных осцилляторов с одной степенью свободы, описываемых уравнением
ф + дф + И' (ф) = и, (9-12)
где q 0 коэффициент диссипации. Например, в работе [227] минимальная амплитуда гармонического воздействия
u(t) = у sin ut, (9.13)
вызывающая выброс решения (9.12) из потенциальной ямы определена путем компьютерного моделирования для двух типовых потенциалов: П(ф) = ф2/2 ф3/3 (иногда называемого потенциалом Гельмгольца), и П(ф) = ф2/2 ф4/4 (соответствующего уравнению Дуф-финга и имеющего две потенциальные ямы, симметричные относительно нуля).
В частности, показано, что для потенциала Дуффинга в системе
(9.12), (9.13) при q = 0.25 выброс неизбежен, если у0.212, и1.07, тогда как при у 0.212 и любых значениях частоты внешнего воздействия выброса не происходит (рис. 9.5 вверху, где у = 0.211, и =1.08).
Как следует из результатов гл. 4, воздействие с обратной связью вызывает выброс при существенно меньших амплитудах.

Действительно, выбирая в качестве Н высоту потенциального барьера и разрешая соотношение (4.31) относительно у, получаем величину воздействия типа (4.25), гарантирующую выброс. Для уравнения
Дуффинга, например, Н = 0.25, откуда 7 = 0.1767, что составляет 83% от величины, найденной в [227]. При этом в законе (4.25) величина Н* может быть произвольной, большей, чем 0.25, и закон (4.25) может быть упрощен:
u(t) = у sign ф. (9-14)
Отметим, что как закон (9.14) так и закон (4.25) не зависят от вида потенциала П(ф), и, следовательно, пригодны для создания резонансного режима в любом осцилляторе, описываемом моделью
(9.12).
Моделирование показывает, что выброс наступает при еще меньших значениях амплитуды входного сигнала (9.14) (см., напр., рис. 9.5 внизу при y = 0.125. Причина этого, по-видимому, в том, что оценки достижимого уровня энергии в замкнутой системе верны не только при выполнении условий приведенных выше теорем, гарантирующих пассивность свободной системы во всем начальном энергетическом слое, но и при некоторых ослабленных условиях, гарантирующих лишь пассивность в среднем (так называемая квазипассивность [61, 68]).

Для рассмотренного случая реально достижимая величина энергии удваивается по сравнению с (4.31). В общем случае выигрыш в мощности, получаемый при возбуждении системы обратной связью зависит, как показывает теорема 4.1, от степени диссипации и растет для слабодемпфированных систем.

На рис. 9.6 показано сравнение уровней возбуждения, требуемых для преодоления потенциального барьера в зависимости от степени диссипации.

Управление химической реакцией с фазовым переходом

Открытие колебательной реакции Белоусова-Жаботинского в 1950-х годах пробудило интерес к колебательным режимам химических реакций. Новые возможности в физико-химических исследованиях и технологиях связаны с управлением колебательными и хаотическими режимами.

Целый ряд интересных явлений? в частности возникновение автоколебаний, имеет место при нелинейном взаимодействии химической реакции в исходной фазе с фазовым переходом, который испытывает продукт реакции. Действительно, с одной стороны химическая реакция поставляет вещество в исходную фазу и тем са-
'О 20 40 60 80 100

Рис. 9.5.

Выброс из потенциальной ямы для системы Дуффинга (вверху гармоническое возбуждение; внизу - возбуждение по алгоритму скоростного градиента).

Рис. 9.6.

Зависимость эффективности обратной связи от степени диссипации при выбросе из потенциальной ямы для системы Дуффинга. Вверху уровень управляющего воздействия, требуемого для преодоления потенциального барьера (А гармоническое возбуждение; В возбуждение с обратной связью по алгоритму скоростного градиента, оценка из вычислительного эксперимента; С возбуждение по алгоритму скоростного градиента, теоретическая оценка из теоремы 4.1).

Внизу эффективность обратной связи: отношение значения (А) к значению (С).
мым ускоряет фазовый переход, с другой новая фаза потребляет продукт реакции, который является катализатором и, следовательно, замедляет химическую реакцию. Такая ситуация характерна для многих методов выращивания тонких пленок, использующих химические реакции, в частности для MOCVD-метода [45, 170].
Ниже, следуя [28], строится алгоритм управления модельной системой, описывающей процесс зарождения тонких пленок из многокомпонентного пара с учетом химических реакций между различными компонентами в исходной фазе. Метод управления основан на линеаризации отображения Пуанкаре (см. гл.6).

Постановка задачи

Рассмотрим химическую реакцию типа А+В ^ С. Будем считать, что концентрация веществ А и В достаточно низка для конденсации их смеси и тем более конденсации А и В по отдельности, но продукта реакции С образуется больше равновесной концентрации С_е, вследствие чего продукт реакции испытывает фазовый переход первого рода [170]. Если С не образует твердых растворов с А и
B, то будет расти пленка вещества С стехиометрического состава. Для определенности предположим, что вещества В на подложке так много, что лимитирует протекание химической реакции только вещество А. Пусть А и С-концентрации соответствующих веществ,^ -скорость химической реакции, Ф(С-С_е) - скорость образования островков новой фазы, N-их концентрация, Ф(^, С) - скорость убыли продукта реакции С в островки новой фазы. Тогда, следуя [170], можно описать кинетику химической реакции и фазового превращения следующей системой уравнений:
( dA/dt = J₀ ф(А, С),
dC/dt = ір(А, С) Ф^, С), (9.15)
{ dN/dt = Ф(С С_е),
где t - время, J₀ - скорость поступления на подложку вещества А. При наиболее часто встречающемся диффузионном режиме роста все островки новой фазы потребляют одинаковое число молекул
C, т.е. Ф^, С) = YNC, где у - коэффициент пропорциональности. Зависимость Ф от С С_е является очень сложной [170]; однако,

от времени т при режиме роста пленок (J = 0.7).
учитывая, что анализ особых точек все равно проводится в линейном приближении и что Ф(0) = 0, ограничимся линейной зависимостью Ф = (3₀(С С_е), где в₀ - соответствующий коэффициент пропорциональности. В качестве скорости реакции р, следуя [170], выберем простейшую функцию с положительной обратной связью: р = К₀АС2, где К₀ - константа реакции. Такая ситуация реализуется, например, когда вещество С является катализатором в реакции между А и В. В этих предположениях система (9.15) примет вид
( dA/dt = J0 КАС2,
\ dC/dt = kAC2 yNC, (9.16)
( dN/dt = в0(С Се).
Данная модельная система, а также ей подобные часто используются для описания различных нелинейных физико-химических явлений, возникающих в дисперсных системах с химическими реакциями: массовая кристаллизация из сложных растворов, осаждение многокомпонентных пленок газофазными методами (в частности, MOCVD-методом[25]), электролиз и т. д. Введением безразмерных переменных: х = АК2/3во1/37_1/3, У = СК2/3во1/3Y-1/3, 2 = Nk1/3в-2/3Y1/3, т = tk-1/3в2/3Y2/3 и безразмерных констант: J = kJo/воY, У0 = СеК2/3 в-1/3 Y-1/3. система (9.16) приводится к следующему виду,

Рис. 9.8.

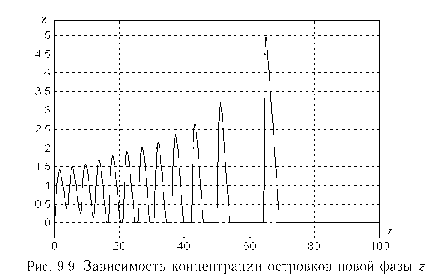
Зависимость концентрации островков новой фазы z от т при устойчивом колебательном режиме роста пленок (J = 0.9).
известному как модель Кукушкина-Осипова [171]:
{dx/dT = J ху2,
dy/dT = ху2 yz, (9.17)
dz/dT = у у₀ (z 0).
Анализ особых точек этой системы в линейном приближении показывает, что точка J = уО 1 является точкой бифуркации, приводящей к образованию устойчивого предельного цикла. Выберем для определенности значение у₀, равное 5/4; тогда бифуркация будет иметь место в точке J1 (5/4)3 1 ~ 0.95.

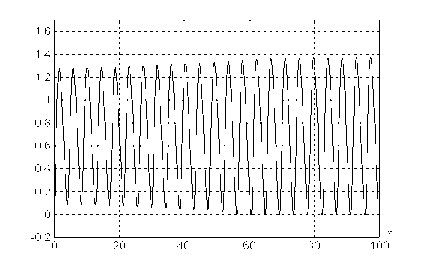
Уточненное значение этой величины, найденное в результате компьютерного моделирования нелинейной системы (9.17), равно J₁ ~0.888 (с точностью 0.0002), т.е. при постоянных потоках J, меньших J₁, система стремится к равновесию (рис.9.7), а при J₁JJ₂^1.049 система испытывает незатухающие колебания, соответствующие устойчивому предельному циклу (рис.9.8). И, наконец, при JJ₂ данный цикл разрушается и рост пленки осуществляется в неустойчивом накопительном режиме (рис.9.9).
В такой ситуации актуальной задачей является управление колебаниями в системе, поскольку структура и свойства пленок зависят

от времени т при неустойчивом накопительном режиме роста (J = 1.2).
от амплитуды и периода колебаний. В частности, возникает вопрос: как нужно изменять во времени внешний поток J, чтобы максимальное значение концентрации островков новой фазы z_max приближалось со временем к заданному значению z*?

Для решения этой задачи в [28] был применен метод адаптивного управления на основе управляемого отображения Пуанкаре [6, 27, 140].

Алгоритм адаптивного управления

Задача управления системой (9.17) ставится как задача поддержания на заданном уровне значений локальных максимумов величины z(t) путем изменения функции J(т) = J₀ + и(т), где J₀ неизвестное значение внешнего потока вещества А, а и(т) подлежит определению. Таким образом, управлением является функция и(т), измеряемой переменной является z(t), а цель управления записывается в виде
\zk - z*\ Д, Д 0, (9.18)
где z_k=z(t_k),т_к время достижения переменной z(t) своего К-го локального максимума, Д - заданная точность. Величина управляющего воздействия и(т) меняется в моменты т_к с учетом измерений величин z_k, причем закон изменения u_k = и(т_к) также изменяется в

от времени т в системе с управлением при г* = 0.9.
ходе процесса по мере уточнения оценок параметров модели объекта управления, вычисляемых алгоритмом адаптации. Особенностью предлагаемого алгоритма является переход от непрерывной нелинейной модели объекта (9.17) к линейной дискретной модели, получаемой путем линеаризации отображения Пуанкаре в точках последовательных локальных максимумов г(т) и перехода к разностному уравнению
гк+і + Аі гк + А2 г- + Аз zk-2 = В ик + В2 ик- + Вз ик-2 + k (9.19) относительно измеряемых величин z_k и управляющих воздействий u_k. В уравнении (9.19) а₁, а₂, а_з, В₁, В₂, В_з - неизвестные коэффициенты, ^_k - ограниченное возмущение (погрешность модели).
Алгоритм адаптивного управления включает алгоритм основного контура, вычисляющий новое значение управляющего воздействия u_k, и алгоритм адаптации, уточняющий оценки b_1k,a_2k,A_3k, b_1k,b_2k,b_3kпараметров модели (9.19). Алгоритм основного контура
uk = [z* + b1kzk + a2kZk-1 + a3kZk-2 b2kuk-1 b3kuk-2]/b1k (9.20)
выбран таким образом, чтобы обеспечить достижение цели (9.18) за один шаг, если оценки совпадают с истинными параметрами модели объекта. Алгоритм адаптации выбирается по методу рекуррентных

Рис. 9.11.

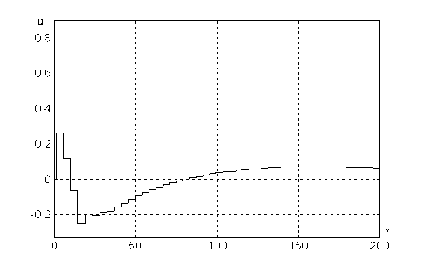
Зависимость управляющего потока и от времени т в системе с управлением при г* = 0.9.

Рис. 9.12.

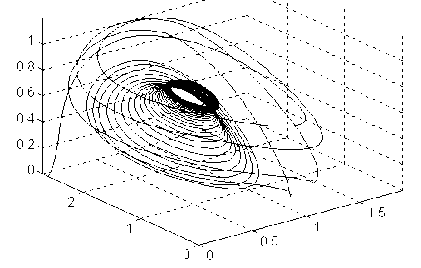
Фазовый портрет управляемой системы в задаче управления г* = 0.9.
целевых неравенств [78, 80] в виде
Ai,k+i
Bi,k+i
®k =
Ai,k a$kгki+\, 1 1,2,3

Рис. 9.13.

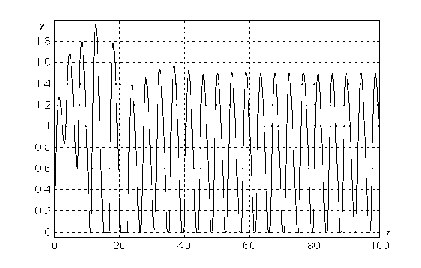
Зависимость концентрации г от времени т при г* = 1.5.
(9.21)
bi,k a$ kuk-i, 1 123,
Zk+i - г*, |гк+і - г* I Д,
0, |гк+і - z*I Д,
где a 0 - коэффициент усиления. На основании результатов [6, 27, 140], можно утверждать, что при выполнении некоторых ограничений на погрешность модели и при достаточно малой величине а цель (9.18) достигается за конечное число шагов, т.е. неравенство (9.18) выполнено для k k* при некотором k*.

Это доказывает принципиальную работоспособность предложенного метода. Отметим, что явный вид правых частей модели (9.17) в алгоритме не используется, т.е. метод применим для широкого класса функций ^, Ф и Ф.

Результаты моделирования

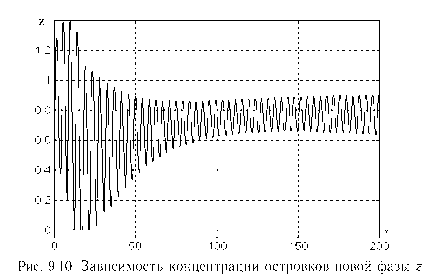
Исследование точности и скорости сходимости алгоритма (9.20), (9.21) было проведено путем компьютерного моделирования. На рис.9.10 и 9.11 приведены зависимости г(т) и и(т), полученные для цели

Рис. 9.14.

Зависимость управляющего потока и от т при z* = 1.5.
(9.18) при z* = 0.9; соответствующий фазовый портрет изображен на рис.9.12. Были выбраны следующие начальные условия и параметры: J₀ = 0.9, х(0) = 0, у(0) = 2.6, z(0) = 0, у0 = 5/4. Видно, что при больших временах и(т) ^ 0.06 (что соответствует J(т) ^ 0.96), причем амплитуда колебаний концентрации островков новой фазы существенно уменьшается и становится примерно в два раза меньше, чем амплитуда колебаний при постоянном и = 0.06 (что соответствует J=0.96). На рис.

9.13-9.15 приведены те же зависимости, но для ЦУ z* = 1.5. Как и следовало ожидать, амплитуда колебаний z(t) в этом случае увеличивается, причем при t ^ ж управление и(т) ^ 0.06 (что соответствует J(т) ^ 0.96).

На рис.9.16 показан процесс настройки коэффициентов модели (9.19).
Из теоретических результатов [27, 140] следует, что порядок модели вход-выход (9.19) должен быть на единицу меньше порядка неуправляемой системы. Представляет интерес вопрос о влиянии порядка этой модели на сходимость и скорость сходимости алгоритма управления.

Компьютерное моделирование показало, что для системы (9.17) сходимость и скорость сходимости слабо зависят от числа коэффициентов модели (9.19). Некоторое уменьшение скорости сходимости обнаружено лишь для адаптивной модели с одним настраиваемым коэффициентом, для которой достижение цели управления

Рис. 9.15.

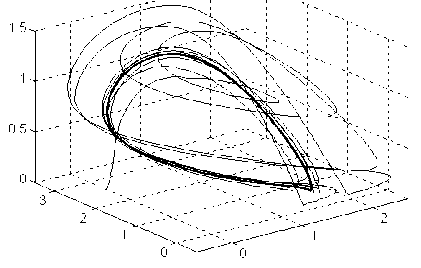
Фазовый портрет управляемой системы при г* = 1.5.

Рис. 9.16. Настройка адаптивной модели третьего порядка
не гарантируется теоремами, доказанными в [27, 140].
Интересно, что поведение системы на больших временах определяется не только асимптотическими значениями внешних параметров задачи, но и тем, каким образом они изменялись в начальные моменты времени, что свидетельствует об эффектах памяти систем, претерпевающих фазовый переход первого рода с химическими реакциями. По-видимому, именно эти эффекты приводят к тому, что многие соответствующие эксперименты, в частности, по выращиванию ВТСП-пленок методом MOCVD, имеют слабую воспроизводимость. Указанный эффект аналогичен явлению затягивания в колебательных системах с двумя степенями свободы, хорошо известному в теории колебаний [46].

Не менее, а, может быть и более необычные эффекты возникают при управлении фазовыми переходами и самоорганизацией систем с учетом пространственной распределенности, см. [26].

Управление диссоциацией двухатомных молекул

Лазерное управление молекулярной динамикой

Задачи управления процессами микромира, в том числе управления движением атомов и молекул имеют богатую историю. Демон Максвелла уже обсуждался во вводной главе. В XX веке были хорошо изучены разнообразные задачи управления процессами химической технологии (в рамках бурно развивавшейся в 1960-1970-х годах химической кибернетики [39, 63]), задачи управления ядерными реакторами [34, 80], задачи управления пучками частиц [66] задачи лазерного управления процессами в твердом теле [57] и др. В традиционных подходах и системах целью управления обычно является регулирование интенсивности процессов, которые могут протекать и без приложения управляющего воздействия.

Однако со времен средневековых алхимиков у людей возникало желание научиться направлять природные процессы по путям, природой не предусмотренным, вмешиваясь в движение отдельных атомов и молекул, разрывая имеющиеся и создавая новые химические связи. В XX веке с изобретением такого тонкого инструмента как лазер, практическая реализация подобных идей стала обсуждаться всерьез.
Главными трудностями при управлении процессами на атомно-молекулярном уровне являются малые пространственные размеры управляемых объектов и большая скорость протекания процессов в них. Средний размер молекул химических веществ (мономеров) имеет порядок ІО-8 м = 10 нм. Среднее расстояние между атомами в молекуле имеет порядок 1 нм, средняя скорость движения атомов и молекул при комнатной температуре ІО2 103 м/с, а период собственных колебаний атомов в молекуле составляет 10100 фс (1 фс=10-15 с).

Создание приборов для измерения и управления в таких пространственно-временных масштабах представляет собой сложнейшую научно-техническую проблему. Отметим, что существующие химические и ядерные реакторы основаны на использовании естественного замедления быстропротекающих процессов.

Например, реализация систем управления ядерными реакциями возможна лишь потому, что динамика нейтронно-физических процессов существенно замедляется из-за наличия так называемых запаздывающих нейтронов, движение которых имеет постоянные времени порядка единиц и десятков секунд. Динамика молекул, вступающих в химические реакции, замедляется за счет диффузии, что создает предпосылки для управления процессами химической технологии.

Однако для тонких задач управления, например для разрыва сильной химической связи при сохранении более слабой (так называемая селективная химия) необходимо избирательно вмешиваться в процессы с характерными временами в пределах фемтосекундного диапазона. Технических возможностей для управления столь быстро протекающими процессами до последнего времени не существовало.
Положение изменилось в конце 1980-х годов с появлением сверхбыстродействующих, фемтосекундных лазеров, генерирующих импульсы длительностью порядка десятков, а в настоящее время и единиц фемтосекунд, а также способов компьютерного управления формой лазерных импульсов. Возникло новое направление в химии фемтохимия, за успехи в котором в 1999 г. была присуждена Нобелевская премия по химии А. Зивейлю [236].

С развитием других способов использования фемтосекундных лазеров возник термин фемтосекундные технологии, или фемтотехнологии.
Предложено несколько подходов к управлению молекулярными системами. В подходе П. Брюмера и М. Шапиро [216] управление основано на интерференции двух лазерных пучков с различными частотами, амплитудами и фазами (схема накачки-гашения pump-dump scheme). Д.Таннор и С.Райс [228] предложили двухимпульс-ные схемы накачки-гашения во временной области. Для оптимизации импульсов впоследствии были использованы методы оптимального управления, в частности на основе метода В.Ф.

Кротова [168]. X. Рабиц с соавторами [118, 162, 197, 209] исследовали различные варианты оптимального управления при классическом и квантовом описании динамики молекулярного движения. В работе [162] была выдвинута идея реализации адаптивного лазерного управления химическими реакциями с применением методов поисковой оптими-зациии (генетических алгоритмов), впоследствии неоднократно подтвержденная экспериментами [89, 92, 195].

О современном состоянии проблемы можно судить по статьям, представленным в сборниках [173, 204], а также в сборнике переводов [76].
Одной из простейших задач этого класса является задача о диссоциации двухатомной молекулы [144, 145, 178, 235]. В то же время эта задача является типичной, на которой удобно сравнивать достоинства и недостатки различных методов. В работе [144] численно были исследованы возможности диссоциации молекулы фтористого водорода (HF) при воздействии периодически меняющегося поля (монохроматичсекого лазерного излучения).

Аналогичным методом в [145] была исследована диссоциация двухчастотным (бихроматиче-ским) воздействием и показано, что интенсивность диссоциирующего поля может быть существенно снижена. В работе [178] получена оценка интенсивности диссоциирующего поля путем нирпирования равномерного изменения частоты внешнего воздействия.

Показана возможность дальнейшего снижения интенсивности поля, требуемой для диссоциации.
Новые возможности для изменения физико-химического состояния вещества возникают при непериодическом воздействии в виде обратной связи. В предыдущем разделе на примере задачи о выбросе из потенциальной ямы показано, что обратная связь позволяет на несколько порядков снизить интенсивность воздействия, требуемую для преодоления потенциального барьера.

При выборе воздействия методом скоростного градиента интенсивность, требуемая для достижения заданного уровня энергии, оказывается обратно пропорциональной степени диссипации системы (см. теорему 4.1), а для консервативных систем соответствующий эффект теоретически может быть достигнут при сколь угодно малой интенсивности возбуждения. Поэтому представляет интерес применение обратной связи для синтеза управления молекулярными системами.
Главные проблемы при управлении с обратной связью это измерение состояния системы и реализация управляющего воздействия на промежутках времени, сравнимых с периодом собственных колебаний молекулы.
В работах [197, 209, 235] и других предложены различные алгоритмы управления с обратной связью, в том числе алгоритмы оптимального управления. Общей их особенностью является то, что они используются для синтеза управляющего воздействия как функции времени по заданной модели молекулярной системы.

В вычислительных экспериментах можно считать, что все нужные сигналы измеряются, а синтезированный алгоритм реализуется в вычислительной машине. В результате будет сгенерирован управляющий сигнал как функция времени, а его реализация на объекте выполняется уже без измерений и без обратной связи.

Практическому применению такого подхода мешает значительное число неопределенностей: не точно известно начальное состояние системы, построенная управляющая функция не точно вычисляется и реализуется с погрешностью. Наконец, сама модель молекулы не точна, поскольку не точно известны ее параметры, да и выбор между классическим и квантовым описанием часто вызывает дискуссии.
Ниже описывается новый подход к задаче о диссоциации двухатомной молекулы [88, 122, 133], основанный на методе скоростного градиента с энергетической целевой функцией. Получаемые алгоритмы отличаются робастностью, поскольку не зависят от формы потенциала межмолекулярного взаимодействия.

Они позволяют достигать диссоциации при меньшей интенсивности управляющего поля по сравнению с чирпингом и более просты для синтеза и расчета по сравнению с методами оптимального управления.

Синтез алгоритмов управления диссоциацией

Идея подходя состоит в том, что задача управления диссоциацией ставится как задача достижения заданного уровня энергии молекулы (порог диссоциации). Для упрощения исследования будем считать, что заданный уровень энергии несколько меньше порога диссоциации, т.е. будем рассматривать задачу предиссоциации.

Затем формируется целевая функция как квадрат отклонения текущей энергии от заданной, строится алгоритм управления по стандартной схеме скоростного градиента (см. гл. 3) и подается на динамическую модель молекулы (эталонная молекула) в течение времени Т₁, достаточного для ее диссоциации.

Если сгенерированный таким образом управляющий сигнал как функцию времени подать на реальную молекулярную систему, то его воздействие приведет к диссоциации лишь тех молекул, начальное состояние которых находится в некоторой окрестности начального состояния эталонной молекулы х₀ (зона диссоциации).

Содержание раздела