Управление взаимосвязанными и распределенными системами

Анализ методов нелинейного управления применительно к задачам управления хаосом показывает, что большинство из них относится к одному из двух подходов: ляпуновскому (метод СГ, методы пассификации) и компенсационному (линеаризация обратной связью, геометрические методы и т. д.). Соотношение между этими двумя подходами можно проиллюстрировать следующим образом.
Пусть цель управления заключается в стабилизации нулевого значения некоторой выходной переменной у = h(x) для аффинной системы X = f(x)+g(x)u. Ляпуновские методы (в том числе метод скоростного градиента) используют целевую функцию вида Q(x) = |h(x)|2 и производят уменьшение ее производной Q согласно условию hTdh/dx(f + gu) 0, осуществляя движение вдоль градиента скорости Q(х) по управлению (т. е. по антиградиенту от Q):
и = -ygT(Vh)h. (6.27)
Видно, что условие малости управления можно выполнить, если коэффициент усиления 7 0 достаточно мал.
Компенсационный подход основан на задании предписанной (желаемой) динамики либо для всего состояния системы, либо для какой-нибудь функции ее состояния. Например, для синтеза алгоритма управления вводится макропеременная а(х) = у + ру, где р 0, значение которой затем обнуляется выбором управления в виде:
/т( ?/г) + ph ?т(?/г)
(6.28)
При этом а = 0, если и только если Q = -2pQ, т. е. компенсация эквивалентна заданию фиксированной скорости убывания Q(х). В результате ценой уменьшения гибкости и отказа от свойства малости управления достигается любая желаемая мгновенная скорость протекания переходных процессов. Заметим, что, в отличие от (6.27), в алгоритме (6.28) присутствует сингулярность (знаменатель в (6.28) может обращаеться в нуль), борьба с которой вносит дополнительные осложнения.

Подобные недостатки свойственны также некоторым методам инверсной динамики [44] и синергетического управления [42], разработанным для управления нелинейными (не обязательно хаотическими) системами.
В заключение еще раз отметим, что, поскольку хаотические системы составляют подкласс класса всех нелинейных систем, методы, разработанные для управления нелинейными системами, обычно применимы и к хаотическим системам. Однако в работах, использующих методы современной линейной и нелинейной теории управления, не всегда уделяется достаточное внимание специфическим свойствам хаотических процессов. Это обычно выражается в том, что опускается требование малости управления. С другой стороны, мощный инструментарий современной теории управления не полностью используется в работах, в которых данное требование учитывается.

В ряде публикаций вводятся нереалистичные допущения (например, считается, что число управляющих воздействий равно размерности вектора состояния системы).

Управление взаимосвязанными и распределенными системами

Задачи и методы управления в распределенных системах

Методы управления колебаниями в пространственно-распределенных (distributed, spatio-temporal) системах во многом опираются на идеи, развитые для сосредоточенных (lumped) систем. Более того, в значительной части работ для синтеза управления используются конечномерные модели объекта управления в виде систем обыкновенных дифференциальных уравнений (ОДУ).

Такие модели могут либо быть получены путем дискретизации по пространству распределенных моделей, описываемых уравнениями в частных производных, либо представлять собой набор ОДУ, описывающих отдельные пространственные элементы (ячейки, клетки), либо получаться отбрасыванием хвоста в разложении по базису в исходном бесконечномерном пространстве состояний (методы Бубнова-Галеркина). В этой главе остановимся на на двух первых вариантах, считая, что ячейки взаимодействуют между собой при помощи связей, отражающих пространственную структуру всей системы, называемой часто массивом (array) или решеткой (lattice).
Типичным классом моделей физико-химических процессов являются так называемые уравнения реакция-диффузия
дх
~ді
еАх + F(x, u),
(7.1)
где х = x(r, t) функция пространственных переменных г еD с Rn и времени Т (возможно, векторнозначная), определяющая состоя-
п д2
ние системы; А = ^ оператор Лапласа, задающий диффу-
1=1 дГ1
зионный тип пространственного взаимодействия элементов. Граничные условия обычно задаются либо периодические: х(а, Т) = x(b, t) при D = [а,Ь] с R1, либо как отсутствие потока через границы
дх
дг
дх
дг
= 0. При дискретизации уравнения (7.1) по
г=Ь
г=а
пространству множество D заменяется конечным числом точек-узлов
г ,
i = 1, 2,...,N, каждому из которых сопоставляется переменная состояния х_і(Т). Динамика величин х_і(Т) определяется как собственной динамикой F(х_і,и_і) так и взаимосвязями с соседними узлами. Например , если пространство одномерно: г Е [а, В], а связи имеют диффузионный характер , получаем систему

Хі = Дхі_і - 2хі + Хі+і) + F (хі, Ui), i = 1, 2, ...,N - 1. (7.2)
Если граничные условия периодические, то дополнительно задается связь х₀(Т) = x_N(Т), а при отсутствии потока через границы накладываются связи х₀(Т) = х₁(Т), x_N1(t) = x_N(Т). Часто отдельно рассматривают случай нулевых условий на границах: х_і (Т) = 0 при і О и при і N. Во многих работах системы дискретизируются также по времени, что приводит к так называемым моделям связанных отображений (coupled maps), или клеточных автоматов (cellular automata):
(7.3)
Хі(п +1)= Хі(п)+?[хі_і(п)-2хі(п)+Хі+і(п)] + hF(xi(п), и(n)) i = 1,... N 1, n = 0,1,2,...
В моделях (7.1), (7.3) управление влияет на динамику каждой ячейки, что соответствует случаю пространственного (полевого) управления. Другой класс задач (граничное управление) возникает, когда правые части в (7.2), (7.3) не зависят от управления, т. е. F(х, и) =
F(х), а управление входит в уравнения граничных ячеек, например
Хо = е(хі - хо) + Fo(x, и) (7.4)
(при периодическом граничном условии). Наибольшей общностью обладают пространственно-неоднородные системы, описываемые (для пространственно-одномерного случая) моделью
!Хі = Fi(Хі, Хіi, Хі+1, u), i = 1,2, ...,N - 1,
Xo = Fo(xo, xi, u), (7.5)
XN = FN(xN, XN^, u).
В качестве целей управления, в дополнение к обычным целям в сосредоточенных системах, рассматриваются различные виды взаимосвязи колебаний в соседних ячейках. Как и в сосредоточенных системах, достижение цели не определяет процесс в системе полностью.
Интерес для исследования представляет определение возможных видов поведения системы с управлением и без него.
К специфическим целям управления в распределенных системах относятся:
стабилизация заданного равномерного (однородного) или пространственно-периодического стационарного поля (стоячей волны);
стабилизация заданного пространственно-периодического нестационарного поля (бегущей волны);
создание или уничтожение спиральной волны (при пространственной размерности не менее двух);
создание или уничтожение заданного неравномерного поля (контрастной структуры, кластеров, паттернов);
управление самоорганизацией и дезорганизацией систем.
Задачи управления распределенными системами систематически рассматривались в теории управления еще в 1960-х годах (см. напр. [17, 18]). Однако интерес физиков к этой тематике, судя по публикациям в физических журналах, существенно вырос лишь в середине 1990-х в связи с интересом к управлению хаосом в распределенных системах. В первых работах по управлению хаосом в распределенных системах в основном повторялись методы, развитые для сосредоточенных систем: метод OGY, запаздывающая обратная связь и т. д. [151].

В последующих работах исследовались (как правило, численно) и другие подходы.
Например, в работе [194] рассматривается одномерный массив из N = 100 ячеек, описываемых логистическим отображением при F(х, и) = 1 ах2 + и, где параметр а задан так, чтобы колебания в каждой ячейке при и = 0 были хаотическими. Проведенные вычислительные эксперименты показали, что локальная обратная связь
(п 1)
иі (п) = у
хі (п)
і = 1,2.....N 1 (7.6)
N + 1 ^ 4 1=0
при достаточно большом коэффициенте усиления у стабилизирует пространственно-однородное распределение х_і = х*, і = 0 , 1, 2 , ..., N. При меньших у стабилизируется неоднородное распределение, состоящее из нескольких кластеров однородности, причем каждая ячейка
колеблется в периодическом режиме. Аналогичное поведение системы наблюдалось при локальной обратной связи по ошибке
Ui(n) = y [хі(n) - x*] , (7.7)
а также при введении более соответствующих реальности глобальных обратных связей, зависящих от наблюдаемых средних значений переменных:
7
N+l
Е 7(n)
- Xj (n - 1)]
(7.8)
Ui (n)
j-o
или
N
Ex (n)
1
N+\
Ui (n) = -y
(7.9)
- x„
j=0
Эти результаты получили обоснование в [142].
В работе [167] рассмотрен случай игольчатого управления (pinning control) одномерной решеткой, когда управление действует лишь на каждую р-ю ячейку, описываемую системой Лоренца. Продемонстрирована возможность стабилизации к пространственно однородному (когерентному), но хаотическому во времени движению, если управление изменяется дискретно во времени по закону (7.7) при Y = 1 и приложено к первому уравнению системы Лоренца.

Этот результат распространен на двумерную решетку из систем Лоренца в работе [223] с использованием интегральной обратной связи, названной в работе адаптивной. Аналогичные результаты получены также для комплексного уравнения Гинзбурга-Ландау
д2 А
А = А + (\ + ірі)т^2 О 4" і/хц)|х41 (7.10)
[182] и для уравнения Свифта-Хоэнберга (Swift-Hohenberg), описывающего динамику лазеров [100]. Уравнение Гинзбурга-Ландау с игольчатым управлением, приложенным в конечном числе точек изучалось в [106, 234]. Уравнение Гинзбурга-Ландау описывает целый ряд явлений в лазерной физике, гидродинамике, химической турбулентности и др., и может представлять разнобразные виды сложного поведения, включая бифуркацию Андронова-Хопфа, хаотические
турбулентные режимы, контрастные структуры и т.д. При помощи вычислительного эксперимента в работе [106] найдено наибольшее расстояние между точками приложения управления, обеспечивающее достижение цели управления.

Аналогичный результат получен при граничном управлении [234].
В работе [218] показана возможность стабилизации решений уравнения Курамото-Сивашинского
(7.11)
др др д2р дАр дt + ^ дг дг2 дгА
периодической запаздывающей обратной связью по скорости
др
~ді
U = ?Т
где т время запаздывания.
Игольчатое управление (local injections) применялось в работе [152] к задаче стабилизации нулевого решения (х_г-(Т) = 0) системы связанных осцилляторов с диффузионно-градиентными связями
(7.12)
%і f(%i) + ota-i ^Хі + Хі₊i) + (X/_ i Хі₊i) + Щ,
а также к уравнению Гинзбурга-Ландау, находящемуся первоначально в хаотическом режиме. Использовалась линейная обратная связь с большим коэффициентом усиления в каждом I-м осцилляторе.

Анализ устойчивости замкнутой системы проводился по линеаризованным вблизи целевого решения моделям.
Минимальная плотность точек локального управления и их оптимальное расположение определены в [146] для одномерного массива связанных логистических систем: f (х) = ах(1 х) в (7.12) при стабилизации линейной обратной свяью. Метод стабилизации неустойчивого пространственного однородного решения уравнения реакции-диффузии предложен в работе[56] на примере комплексного уравнения Курамото-Цузуки.

В работе [232] предложен метод подавления хаоса и спиральных волн в уравнении Максвелла-Блоха с дифракционными связями слабым пространственным возмущением.
Интересные задачи кластерной синхронизации в двух- и трехмерных массивах нелинейных осцилляторов рассматривались в работах [96, 97, 98, 201]. На основе функций Ляпунова специального вида найдены условия разбиения массива на заданное число
компактных кластеров осцилляторов, колеблющихся синхронно. Показано, что с ростом степени взаимосвязи число кластеров уменьшается, вплоть до полной синхронизации. Хотя в перечисленных работах управление в явном виде не присутствует, их результаты можно интерпретировать как выбор коэффициента связи К, обеспечивающего заданную степень кластеризации в системе.

В развитие этого направления можно поставить задачу адаптивного управления коэффициентом связи, осуществляемого в ходе экспериментов с системой.

Управление анергией в моделях синус-Гордона и Френкеля-Конторовой

Продемонстрируем возможность применения метода скоростного градиента для управления системами типа синус-Гордона по энергети-
_ . дх д2х дх
ческим критериям. Введем обозначения x_t = , х_и = -гтг, х_г = ,
dt дТ2 г д r
д2 х д2 х
x_r._t = д dt Хт = ~д2 И РассмотРим системУ описываемую уравнением синус-Гордона с диссипацией
Jx_tt = КАх Е sin х px_t, (7.13)
где х = х(г, t) - функция состояния системы; г е X с Мп - пространственная переменная, изменяющаяся на множестве X; A - оператор
Лапласа: Ах = ^ х_ГіГі; J, k, р - параметры системы; Е = Е(Т) - внеш-
і=і
нее воздействие (например, напряженность внешнего электрического поля). Будем считать, что Е = Е₀ + u(t), где Е₀ - базовый уровень поля, и(Т) - управляющее воздействие. Систему (7.13) можно рассматривать как модель массива диффузионно связанных осцилляторов (например, маятников, жидких кристаллов и т.д.), каждый из которых размещен в точке г. Тогда х(г, Т) - угол поворота осциллятора.

Система относится к классу моделей реакция-диффузия, но имеет важное самостоятельное значение.
Поставим задачу вывода энергии свободной системы
H=\j (7 (§7) +/elV^|2 + 2?o(l-cos x)^j dr (714)
x
получим, что V 0 при
на заданный уровень И,, т. е, введем цель управления
(7.15)
lim И(Т) = И,,
t ОО
Положим сначала р = 0 и вычислим скорость изменения энергии вдоль движений системы (7.13), считая u(t) = и постоянным
(_
dt
= Jx_t - x_tt kAxx_t + E₀ sin x - x_tdr =
(7.16)
= J x_t ( E sin x + E₀ sin x) dr = u(t)J x_t sin xdr
Видно, что если выбрать управление в виде
u(t) = jJ x_t sin xdr,
где j 0, то энергия И(t) будет неубывающей функцией времени.
1 2
Если же ввести функцию V(t) = ~{H(t) Я*) , то, рассматривая
величину
= u(t)(H (t) И,) J x_t sin xdr,
dV
dt
(7.18)
(7.19)
(t) = j(H (t) И,) J x_t sin xdr,
t. e. воздействие (7.19) приближает систему к достижению цели.
Рассмотрим пространственно-одномерный, пространственно-дискретный вариант задачи
_k ( ) ( )
Jxj = -j~2 (x_/+i-2x_/+x_/-i)-(E₀+^(0) sinXj-pXj, /=1,2,... ,N, (7.20) соответствующий непрерывной системе
Jx_tt = kx_rr (E₀ + u(T)) sin x px_t (7.21)
141
на множестве X = [а, Ь], где Xj = x(jh/b а).
Система (7.20) есть не что иное как управляемая версия классической модели Френкеля-Конторовой, (см., напр., [46]), предложенной в 1939 году, исследованию свойств которой посвящено много работ.
Обычно при исследовании системы без управления выбирают в (7.21) либо нулевые граничные условия х(а, Т) = x(b, Т) = 0. соответствующие в дискретной модели (7.20) соотношениям
(7.22)
Хо(Т) = Xn +і(Т) = 0,
= 0, соответствующие
(7.23)
либо периодические условия х_г
Х0 = Хі,
= х_г
r=a \r=b
XN = XN +1.
Задача управления энергией цепочки может быть решена на основе результатов гл. 3. Алгоритм управления энергией, полученный методом скоростного градиента имеет вид
N
u(t)= y(H (t) И,) Е Xj sin Xj, (7.24)
j=i
где у 0. Из теоремы 3.1 следует, что цель управления (7.15) в системе (7.20), (7.24) при g = 0 достигается, если энергетический слой между уровнями И(0) и И, не содержит равновесий системы, удовлетворяющих условиям sin Xj = 0, j = 1,... ,N.
Отметим, что в частном случае N = 2 при граничных условиях (7.23) система приобретает вид
2k
J'X\ = 2 Хі) (Eq + u(t)) Sinxi px 1,
(7.25)
Jx = ¦ (a'i - X) - (E, + ltd}) sinx₂ - px.
В этом частном случае задача управления энергией близка к задаче о синхронизации двух маятников, рассматривавшейся в п. 5.4.
Дискретный вариант алгоритма управления (7.19) имеет вид
и(Т) = ₇(И(Т) И,) (х₂ х0( sin х₁ sin х₂), (7.26)
142
где Н(Т) определяется дискретным вариантом (7.14)
Н = (х\ + if) + I (х\ - х₂)2 + Е₀ (2 - cos х\ - cos х₂). (7.27)
Построенные алгоритмы управления можно применять для исследования свойств нелинейных колебательных систем в различных задачах. В частности, в ряде практических задач необходимо управлять колебаниями осциллирующих частиц: например, ориентировать частицы в заданном направлении, менять ориентацию частиц в жидких кристаллах с продольной на поперечную и т. п. с а) на б):

Рис. 7.1.

Непрозрачная (а) и прозрачная (б) структуры.
Если принять, что угол x(r, Т) ориентации частиц подчиняется уравнению (7.13), то добиться перехода из структуры с продольной ориентацией а) в структуру с поперечной ориентацией б) можно, меняя ориентацию (поляризацию) постоянного внешнего поля Е. Однако, для этого изменение поля SE должно быть значительным и, по крайней мере, превосходить начальное поле Е₀.
В то же время, используя алгоритм управления с обратной связью типа (7.19), можно заставить ориентацию кристаллов изменяться наподобие колебаний маятников. При этом, если в качестве Н выбрать величину, близкую к Н = Е₀(В а) - энергии состояния, соответствующего конфигурации б) и если степень диссипации д О мала, то алгоритм (7.19) при весьма малом у, т. е. при маломощном дополнительном управляющем воздействии, сможет заставить частицы значительную часть времени проводить вблизи конфигурации б), т. е. сделать кристалл высокопрозрачным.

Управление волновым движением в цепочке маятников

Модель цепочки маятников. Рассмотрим, следуя [75], задачу управления возбуждением колебаний в цепочке из N последовательно соединенных математических маятников.

Такая модель встречается при описании различных физических и механических систем (см., напр., [46, 160]). При отсутствии трения система связанных маятников описывается уравнениями
?і(0 + W₀sin fii(t) = Цф2(Т) - фЛ)) + u(t),
Фі(T) + ^0 sinФі(t) = k(Фж(Т) - 2(fii(t) + ф_Ж(Т)), ₍₇₂₈₎
1 (i = 2,3,..., N - 1), (728) „ ?N(t) + u0 sin ф2(Т) = k(фN-1(t) фN(t)),
где ф_і (t) (i = 1,2, ...,N) - углы поворота маятников; u(t) - приложенный к первому маятнику момент внешних сил, выраженный в единицах углового ускорения (управляющее воздействие); и, k -параметры системы: и₀ - собственная частота малых колебаний изолированных маятников, k - параметр взаимодействия маятников (например, коэффициент упругости пружин).
Введем вектор состояния системы x(t) Е R2N как х(Т) = = col {фь ф₁, ф₂, ф₂,..., ф^[, ф_N}. Полная энергия системы (7.28) Н(х) определяется выражением
N
Н (х) = ^2 Hi (х), где
1=1
( Hi(х) = 0.5ф2 +и0(1 cos фі) + 0.5К(фі+1 фі)2 I (i = 1,2,..., N 1), (7.29)
[ Hn(х) = 0.5ф2+и0(1 cos фN).
При отсутствии управления рассматриваемая модель совпадает с моделью цепочки Френкеля-Конторовой, в которой пренебрегли трением. Главное отличие от задачи, рассмотренной в предыдущем параграфе характер вхождения управления.

В отличие от задачи, рассмотренной ранее, в данном параграфе изучается случай, когда управление локализовано и воздействует только на один маятник. На языке распределенных систем этот случаи соответствует граничному управлению.
Рассмотрим также систему циклически соединенных маятников, которая описывается уравнениями, аналогичными (7.28), но включающими также упругую связь между первым и последним маятником:
^(О+цЦіп фЛ) = К( ф₂(Т) - 2^\(t) + y_N (t)) + u(t),
фі (t)+wsin Pi (t) = k( ф_Ж(Т) - 2ф, (0+ф_Ж(Т)) _{( )}
1 (i = 2,3,.. .,N - 1), (A3U) , фм(t)+u% sin PN(t) = k(ip_N-i(t)-2фы(T))+ фі(Т)).
Соответственно изменяется и выражение для полноИ энергии системы:
N
Н (х) = ^ Hi (х), где
і=і
[ Hi (х) = 0.5 ф2 +и(1 - cos фі) + 0.5К(ф;+і - фі )2 (і = 1, 2,... ₍N - 1), (7.31)
[ Нм(х) = 0.5 ф2+и(1 - cos фм) + 0.5 k(ф1 - фм)2.
Уравнения (7.30) симметричны относительно собственных движении маятников (первыИ маятник является выделенным только в силу того, что к нему приложен момент управления). Эта симметрия уравнении приводит к тому, что для данноИ системы упрощается достижение цели управления, состоящей в синхронизации колебании маятников.
Постановка задачи и синтез алгоритма управления. Задачу возбуждения волны колебаний с заданной амплитудой будем трактовать как достижение заданного уровня энергии системы с дополнительным требованием того, чтобы маятники имели противоположные фазы колебаний.

Синтез алгоритма управления выполним по методу скоростного градиента.
Для применения метода введем частные целевые функции
@ф(фЬ ф2) = .5 S'2, ₍₇₃₂₎
Qh(х) = 0.5(Н(х) - Н*)2, ( )
где 5_Ф = ф₁ + ф₂; Н(x(t)) - полная энергия системы; Н* - ее заданное значение.
Минимальное значение функции Q_ф соответствует требованию противофазности колебаний первого и второго маятников (во всяком случае при малых начальных фазах ^і(О), ф₂(0) тождество Q_v(ф₁, ф₂) = 0 выполняется только тогда, когда ф₁ = ф₂). Минимизация Q_H означает достижение желаемой амплитуды колебаний.
Введем общую целевую функцию Q(х) как взвешенную сумму Qtp и Q_H, а именно
Q(х) = aQ^(фі, Ф2) + (1 aQ(х), (7.33)
где a (0 a 1) - заданный весовой коэффициент.
Выполнение процедуры метода скоростного градиента с целевой функцией Q(x) приводит к закону управления в конечной форме, имеющему вид
u(t) = у (а5ф(t) + (1 а)5н(Т)фі(Т)) ,
5ф (t) = фі(т) + ф2(t), (7.34)
5н (t) = Ht Н *.
Отметим, что вычисление управляющего воздействия требует измерения угловых скоростей первого и второго маятников, а также полной энергии всей системы маятников.
Результаты моделирования процесса возбуждения и синхронизации колебаний. Приведем некоторые результаты моделирования процесса возбуждения колебаний по алгоритму (7.34).
Для определенности при экспериментальном исследовании рассмотрим цепочку из N = 50 маятников.
На графиках показаны результаты моделирования системы (7.28) с алгоритмом управления (7.34) при 7 = 0.8 и различных значениях параметра а. Рис. 7.2 - 7.4 относятся к случаю a = 0, в котором целью управления является обеспечение заданного уровня полной энергии системы.
Как видно из графиков, данная цель управления достигается, H_t ^ Н* (Н* =4), но движение маятников носит нерегулярный (хаотический) характер и вторая цель управления не достигается (см.

Рис. 7.2.

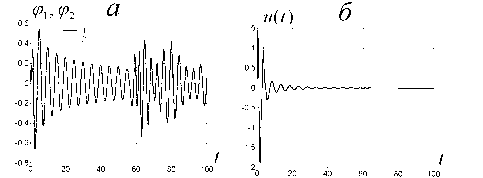
Переходные процессы по ^, ^₂ и сигнал управления. N = 50, а = 0.

Рис. 7.3.

Целевые функции Q^ и Н_т. N = 50, а = 0.
рис. 7.3).

Видно также, что по мере достижения требуемой энергии сигнал управления затухает.
Причина нерегулярного поведения маятников проясняется из рис. 7.4. На данном рисунке видно, как прямая волна колебаний распространяется: при t ~ 30 она достигает последнего маятника, после чего навстречу распространяется обратная волна. Наложение волн создает сложную картину колебаний.

Процесс возбуждения колебаний при а =1 показан на рис. 7.5, 7.6.

Как видно их представленных графиков, здесь также не удается обеспечить противофазного движения маятников. При промежуточных значениях 0 а 1 характер процессов качественно не меняется по сравнению с рис.

7.2 - 7.4).
Причина неудовлетворительного поведения системы по отношению к цели по-видимому, в том, что противофазное движение маятников без управления не является инвариантным, т. е. при u(t) = 0 это движение, возникнув, не будет сохраняться в дальнейшем. Для подтверждения этой гипотезы рассмотрим рис. 7.7, на котором отражены свободные колебания системы из 50 маятников, все начальные условия в которых выбраны в противофазе (^₁₊₁(0) = ^(0), I = = 1,2,...,N 1).

Возникающие на границах эффекты отражения волн приводят через некоторое время к искажению картины колебаний, причем в первую очередь - для маятников, находящихся вблизи от граничных (первого и последнего).

Содержание раздела

---