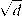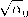Свойство раскачиваемости

А2. Наибольшее инвариантное множество М а D₀ свободной системы (т. е. множество целых траекторий системы (3.4), содержащееся в D₀), где D₀ = {x : {И₀(х), H(x)} = 0}ПП₀ состоит из не более чем счетного числа изолированных точек без конечных точек сгущения.
Тогда любое решение системы (3.2), (3.12) либо обеспечивает цель (3.3), либо стремится к некоторой точке из D₀, являющейся равновесием свободной системы (3.4). Кроме того, множество начальных условий, из которых решение системы (3.2), (3.12) стремится к неустойчивому равновесию свободной системы, имеет меру нуль.
Следствие 3.1. Если множество D₀ из условия А2 пусто, т. е. {И₀, Н}(х) = 0 при х е П₀, то цель управления достигается при любых начальных условиях х(0) е П₀.

В этом случае можно показать [бі], что построенная система обладает свойством частичной асимптотической устойчивости по отношению к целевой функции QM.
Теорема 3.1 может быть выведена из более общих результатов [61, 140]. Однако полезно провести ее непосредственное доказательство.
Доказательство теоремы 3.1. Вычисление производной от функции Q_t = (И₀(р(Т), q(t)) И*)2/2 вдоль решений системы (3.2), (3.12) дает
Qt = ^(z(T))T z(t), (3.15)
где z(T) = [Н₀(х(Т)),И₁(х(Т))]т(И₀(х(Т)) И*). Следовательно, Q_t 0 и Q_t не возрастает, т.е.

Q_t Q₀. Это значит, что решение полной системы никогда не покидает множество П₀. Ограниченность правых частей системы (3.2), (3.12) гарантирует, что ее решение х(Т) определено при всех Т 0. Следовательно, существуют пределы limt^ Qt = Qи Іітт^то Нз(х(Т)) = И_ж.

Если И_ж = И*, то теорема доказана. Предположим, что И_ж = И*.

Из условия теоремы следует, что функции z(t), ф(г(і)), Q_T, Q_T ограничены при x(t) e П₀. Далее для доказательства требуется следующее вспомогательное утверждение.
Лемма 3.1 (лемма об аттрактивности) [140]. Пустъ для системы X = f (х, і), х e t 0 существуют гладкая неотрицательная функция V(х, і) и функция w(x, і) такие, что ?(х, і) w(x, t) О для любых t to, x e Mn, где V(x,t) = %f(x,t).

Предположим, что ограниченность V(x, t) влечет ограниченность f (x, t), равномерную непрерывность w(x, t) no x и ограниченность dw/dt.
Тогда функция V_t = V(x(i), t) ограничена на интервале [i₀, то) и
lim w(x(i), t) = 0. (3.16)
i^x
Если, кроме того, V(x, t) w₁(|x|) для некоторой скалярной функции w₁(r) такой, что w₁(r) ^то при г ^то, то функция x(t) также ограничена.
Применяя лемму об аттрактивности, получаем, что Q_t ^ 0. Из условия строгой псевдоградиентности и непрерывности ф следует, что и(і) 0 и z(t) 0 при t -^то. Поскольку, по предположению, Н_ж = И*, получаем что [И₀, H₁](x(t)) ^ 0. Первая часть теоремы доказана.
Для доказательства второй части выберем е 0 из предположения А1 при с = И_ж. В силу А1, для достаточно больших t 0 решение x(i) входит в множество D_e,_H^ и остается в одном из его ограниченных связных компонентов.

В силу компактности замыкания этого компонента существует хотя бы одна предельная точка траектории x(i) и все предельные точки x(i) удовлетворяют равенству [Н₀, И₁]=0, т.е. x(i) сходится к множеству D₀ = {x :[Н₀, И₁]=0}П 0₀. Применяя теорему Ла-Салля и учитывая условие А2, устанавливаем, что существует Ит_Т^_ж x(t) = x_M e D₀ и x_M точка равновесия системы (3.2), (3.12).

Пусть А_ж матрица Якоби системы, вычисленная в точке x_M, a M_s, М_и, М₀ устойчивое, неустойчивое и центральное многообразия системы в точке x_TO. Из теоремы о центральном многообразии [29] следует, что x(i) ^ x_M только при x(0) e M_s0М₀, если |x(0) x^l достаточно мало.

Пусть x_M неустойчивое равновесие, т.е. М_и не пусто. Тогда dim(M_s 0 М₀) 2п.

Выполняя сдвиг назад вдоль траекторий свободной системы, легко показать, что все начальные условия х(0) такие, что х(Т) ^ х_ж принадлежат некоторому многообразию размерности меньшей, чем 2п. Так как множество всех возможных неустойчивых предельных точек не более чем счетно, множество соответствующих начальных условий имеет нулевую лебегову меру в М2п. ¦
Замечание 3.2. Пусть гамильтониан управляемой системы имеет вид Н(q, р, и) = Ho(q, р) + Hi(q, р)ти при
Ho(q,p) = ^ртЩУ'р + ПО), Hi(q,p) = q, (3.17)
где q, р - n-мерные обобщенные координаты; A(q) - симметрическая положительно определенная матрица кинетической энергии; n(q) О - потенциальная энергия. В этом случае справедливо соотношение р = A(q)q и уравнения системы могут быть преобразованы к лагран-жевой форме:
d 1 _т д
Yi (A(q)q) ~2i,dq ч+ ?п^= и- Ш8)
В новых координатах энергия примет вид
Ho(q, q) = 7;qTA(q)q + ІВД. (3.19)
Равновесия свободной системы имеют вид (0,^), где q - стационарная (критическая) точка потенциала n(q) (т.е. ?П(^) = 0). Предположим, что все стационарные точки функции n(q) изолированы. Тогда из теоремы 3.1 следует, что если начальный энергетический слой

По = {(Q,Р) : Но Ho(q,р) Н*}
(при Но Н*) или
По = {(q,р) : Н* Ho(q,р) Но}
(при Но Н*) не содержит минимумов потенциала n(q), то для почти всех решений достигается цель (3.3). Кроме того, если матрица A(q) равномерно положительно определена, т. е. pTA(q)p р\р\2 для некоторого р 0 и всех р е Rn, то, как нетрудно показать,
почти все решения замкнутой системы приближаются к множеству 5 = {(q,р): Ho(q,р) = И*}. ?
Пример 3.1 (окончание). Применительно к маятнику (3.8) замечание 3.2 означает, что если начальный энергетический слой между уровнями Н₀ и И* не содержит равновесий, то уровень И* будет достигаться при всех начальных условиях, а если начальный слой содержит только неустойчивые равновесия (n(2k + 1),0), k = ±1, ±2,..., то цель (3.3) будет достигаться при почти всех начальных условиях. ?
Приведем формулировки результатов для лагранжевых систем более общего вида.
Теорема 3.2 [61, 140]. Рассмотрим голономную лагранжеву систему, находящуюся под действием потенциальных, гироскопических и управляющих обобщенных сил:
N N
+ Dij(q)qi + b,_ju_j,
J-i j=i
д_дТ_ _ ЭТ_ dt до[і дуі
i 1,..., n, (3.20)
дЦі
где q_i - обобщенные координаты; q_i - обобщенные скорости; d_ij dj_i; T = ^qTA(q)q кинетическая энергия; П = n(q) потенциальная энергия. Пусть матрица A(q) равномерно положительно определена, detВ 0, где В {b_ij}, функции Vn(q),D(q)
{d_ij(q)}, A_1(q) ограничены на множестве О, имеющем при Н₀ И* вид О {(q, q) : Н₀ И И*}, а при при Н₀ И* вид О {(q, q) : н* И Но}, где Но И(q(0), q(0)). Пусть, наконец, внутренность О не содержит положений равновесия свободной системы.
Тогда алгоритм
U y(q, q)(H - н*)вб q (3.21)
обеспечивает достижение цели
lim И(q(t), q(t)) И* (3.22)
t^x
в системе (3.20), (3.21) при 0 y(q, q) у, где у 0 любое положительное число.
Частным случаем рассмотренной задачи является классическая задача гашения (демпфирования) колебаний, в которой И* = inf n(q). Считая для определенности n(q) О, П(0) = 0, приходим к следующему хорошо известному результату.
Следствие 3.2 (теорема Красовского-Румянцева). Пусть n(q) положительно определенная функция, а начальный энергетический слой не содержит положений равновесия, кроме q = q = 0. Тогда это положение может быть сделано асимптотически устойчивым при помощи обратной связи и = YBTq при любом 7 0.
Замечание 3.3. В работах [220] [222] приведены обобщения приведенных выше результатов на задачи управления инвариантами негамильтоновых нелинейных систем.

Охвачены случаи, когда число управлений меньше числа обобщенных координат (т п), управление входит в модель нелинейно, функция ф(г) негладкая. В частности, в [222], что алгоритм и = 7 sign ((И H*)BTq) обеспечивает достижение цели (3.22) в системе за конечное время.

Свойство раскачиваемости

Как уже было сказано, в задачах управления колебаниями существенным является выполнение дополнительного требования малости управляющего воздействия. Возникает проблема: какие цели могут быть достигнуты при помощи малого управления?

В частности, до какого уровня энергии можно разогнать консервативную систему сколь угодно слабым управлением. Введем следующую терминологию.
Определение 3.1 [125]. Система X = F(х, и, Т) называется раскачиваемой по отношению к цели
lim Q_t = g, g e G C R1, (3.23)
t^x
если для любого s 0 и любого g e G существует закон управления
u(T) = U_g,_s {x(s), 0 5 t} , (3.24)
такой, что |u(T)| s и цель (3.23) в замкнутой системе достигается. При этом закон (3.24) называется раскачивающим по отношению
к G. ?
Из теоремы 3.1 следует, что любая гамильтонова система, удовлетворяющая условиям А1, А2, раскачиваема по отношению к цели (3.3) при почти всех начальных условиях, если стационарные точки потенциала n(q) изолированы и в начальном энергетическом слое нет устойчивых равновесий системы, т. е. Я* sup^II(g), где верхняя грань берется по всем локальным минимумам n(q), находящимся в начальном компоненте связности энергетического слоя П₀. Действительно, правые части замкнутой системы ограничены в области П₀ и управление может быть сделано сколь угодно малым путем выбора достаточно малого коэффициента 7. Разумеется, уменьшение коэффициента усиления 7 приводит к росту времени достижения цели, но принципиальная достижимость цели остается неизменной.
Интерпретируя условия А1, А2 теоремы 3.1 как достаточные условия управляемости системы по отношению к энергии, можно, допуская некоторую вольность, сформулировать результат теоремы 3.1 как закон преобразования системы обратной связью:
Если система управляема по отношению к энергии, то значение энергии свободной системы можно изменить на произвольную величину при помощи сколь угодно малой обратной связи.

Управление первыми интегралами

Полученные результаты распространяются на задачи достижения более сложных целей, чем стабилизация уровня энергии. Ниже рассматривается задача о стабилизации на заданных уровнях нескольких инвариантов (первых интегралов) свободной системы [61, 135].
Пусть задано k скалярных инвариантов G_i(q,р), і = 1,... , k, т. е. {Я₀, Gi} = 0, і = 1,... ,k, и пусть цель управления задана в виде
lim Gi(p(t), q(t)) = G*, i = 1,..., k, (3.25)
t^x
где G* заданные числа. Введем целевую функцию
1 _т
Q(q.p) = 2 (0(9, Р) - GyR(G(q,p) - G*), (3.26)
где G(q,p) = col {Gi(q,p),... ,G_k(q,p)}; G* = col {G*, ... ,G*}, а матрица R = RT О размера k x k симметрична и положительно определена. Тогда алгоритм скоростного градиента, построенный по цели (3.25), (3.26), можно представить следующим образом:
и = -7 {Я, Q} = -7 {Я, G) R (G(q, р) - G*). (3.27)
Здесь Н обозначает вектор-столбец с компонентами, составленными из гамильтонианов взаимодействия Hj, j = 1,... , m, т. е. скобка {H,Q} есть вектор-столбец с компонентами {Hj,Q}, а скобка {H,G} представляет собой матрицу-функцию размера т x k с элементами вида {Hj, Gi}.
При выводе выражения (3.27) используется правило дифференцирования функции V(q, р) вдоль траекторий гамильтоновой системы с гамильтонианом Н(q, р): V = {Н, V}.
Можно рассмотреть и более широкий класс алгоритмов
и = -ф({НМ}), (3.28)
где ф(у) вектор-функция со свойством ф(г)1г 0 при z = 0.
Для формулировки условий применимости алгоритмов (3.27) и (3.28) предположим, что функции Н_і, G_l бесконечно дифференцируемы, и введем множество
S(q,p) = span { ad^₀ {H,G} , s = 0,1,...}, где векторы adH определены индуктивно:
adHG = G, adHG = {H, G}, adH+1 G = {H,adHG} .
Вновь рассмотрим гамильтонову систему
т
q = VpHo(q, р) + VpHjUj,
(3.29)
J=i
т
p = -VqHo(q,p) -^2 VqHjUj.
j=1
Теорема 3.3 [135, 221]. Пустъ функции Hj, ф бесконечное число раз дифференцируемы и Hj ограничены вместе со своими первыми и вторыми частными производными на множестве
По = {(q,р) : Q(q,р) Qo}
для некоторого Q₀ 0. Пустъ G_i, i = 1,... ,k, набор бесконечно дифференцируемых инвариантов свободной системы (3.4). Предположим, что существует 5 0 такое, что каждый связный компонент множества
D5 = Пор {(q, Р) : det РФ А 5} ,
где А = {Я, G} ограничен, и выполнено следующее условие (условие Ширяева):
dim S(q, р) = k (3.30)
для всех (q, р) е П₀, таких что G(q, р) = G*.
Тогда цель управления (3.25) достигается на любой траектории системы (3.29), (3.28), начинающейся в П₀.
Замечание 3.4. В случае, когда целевое множество
П* = {(q,р) : Gi(q,р) = G*, і = 1,... ,k}
вырождается в точку, условие Ширяева (3.30) означает детектируе-мость состояния П* свободной системы. Если k = 1 и G₁ = Н₀, то рассматриваемая задача превращается в задачу управления энергией и условие Ширяева означает, что {Н₀,Н₁} = 0 при (q,р) е П₀, Ho(q,р) = Н*. ?
В общем случае условие Ширяева (3.30) гарантирует детектиру-емость целевого множества в свободной системе, что в свою очередь влечет за собой управляемость системы относительно множества П*.
Замечание 3.5. Если условие (3.30) нарушается в счетном числе изолированных точек, являющихся неустойчивыми равновесиями свободной системы, то, как следует из теоремы П.1, цель (3.25) будет достигаться для почти всех траекторий замкнутой системы, начинающихся в П₀. ?
Замечание 3.6. Если множество П₀ компактно (например, если целевая функция Q радиально неограничена: Q(q, р) ^ ж при
\p\ + M ^ ж), проверка свойств множества D$ становится ненужной. ?
Вновь допуская некоторую вольность, сформулируем результат теоремы 3.3 как закон преобразования системы обратной связью:
Если система управляема по отношению к некоторому набору инвариантов, то их значения можно изменить на произвольные величины при помощи сколь угодно малой обратной связи.

управление диссипативными системами

Устанавливаются пределы преобразования энергии управляемых гамильтоновых систем при заданных уровнях управления и диссипации. Вводятся понятия индекса возбудимости и резонанса с обратной связью для нелинейных систем. Изучается возможность создания резонансных режимов в нелинейных системах при помощи управления с обратной связью.

Приводятся результаты оценки индекса возбудимости одно- и двухмаятниковых систем путем компьютерного моделирования.

Анализ возбудимости систем с диссипацией

Перейдем к рассмотрению задач управления системами, в которых присутствует диссипация, (точнее, тех задач, где диссипацией нельзя пренебречь). Отправляясь от гамильтонова описания управляемых систем (3.1), будем рассматривать гамильтоновы системы с диссипацией, описываемые уравнениями
dH(q,p, и)
%
дН(д,р, и) dpi
Ri (q, р), і = 1,
(4.1)
Ні =
Hi =
n,
где q = co1(q₁,..., Q_n), р = со1(рь...,р_п) векторы обобщенных координат и обобщенных импульсов, образующие вектор состояния системы х = co1(q, р); Н = Н(q, р, и) гамильтониан управляемой системы; u(T) е Rm вход (вектор внешних обобщенных сил); R(q,р) = co1(R₁(q,p),...,R_n(q,р)) функция диссипации, удовлетворяющая условию
R{q,p)ldH^_pP) 0, (4.2)
где H₀(q,р) = Н(q,р,0) энергия свободной системы. Неравенство (4.2) означает рассеяние энергии на свободных движениях системы: Но 0.
Ясно, что диссипация затрудняет управление энергией системы, в частности, накачку энергии внешними воздействиями. Поэтому такие свойства как раскачиваемость для диссипативных систем не характерны. Интерес представляют оценки возможности преобразования энергии систем при заданных уровнях управления и диссипации.

Особо интересен случай малой диссипации (слабодемпфирован-ных систем), для которого характерны колебательность процессов в системе и наличие резонансных явлений. Ниже устанавливаются пределы возможного преобразования энергии управляемых гамильтоновых систем при заданных уровнях управления и диссипации, а также возможность создания резонансных режимов в нелинейных системах при помощи управления с обратной связью.

Пассивность и диссипативность

В целях большей естественности и удобства изложения расширим класс рассматриваемых систем и будем изучать системы, описываемые нелинейными дифференциальными уравнениями состояния
Х = F(х, и), у = h(x), (4.3)
где x, u, у векторы состояния, входов и выходов, соответственно. Предполагается, что входная функция (управление) u(t),0 Т то принадлежит заданному классу допустимых управлений U. Формулировка свойства диссипативности для таких систем в наиболее общей форме была дана в 1972 г. Я. Виллемсом [233], который ввел следующее определение.
Определение 4.1. Пусть задана скалярная функция w(x, и) такая, что для любого t 0, любого начального состояния
х (0) = х₀ и любого допустимого управления u(-) е U выполнено
t
J\w (x(s), u(s)) \ds +то, где x(T) решение системы (4.3). Систе-0
ма (4.3) называется диссипативной относительно функции w(x, и), если существует непрерывная неотрицательная функция V(х) такая, что для любого Т 0 и любого решения х(Т) системы (4.3) при и(-) е U выполнено неравенство
t
' w(x(s), u(s))ds.
V(х(Т)) V(х(0)) +
(4.4)
0
Функция w наывается функцией расхода системы (4.3) (supply rate function), функция V называется функцией запаса системы (storage function), а неравенство (4.4) неравенством диссипации (Dissipation inequality). ?
Особую важность имеют следующие частные случаи. Система (4.3) называется
а) пассивной, если число входов равно числу выходов (dim U = dim Y = т) и система диссипативна относительно функции расхода
w(x, u) = у u = h(x) u;
б) строго пассивной, если dim U = dim Y = т и система диссипативна относительно функции расхода w(x, u) = yTu в(х), где в(х) 0 при х = 0. (Предполагается, что начало координат точка равновесия системы).
Функция запаса V(х) является аналогом энергии для систем общего вида, произведение входных и выходных величин выражает измеренную мощность, поступившую в систему, а функция /3(х) оценивает снизу скорость рассеяния энергии в системе. Таким образом, неравенство диссипации (4.4) является обобщенным выражением баланса энергии. В частном случае, когда система пассивна, а неравенство диссипации записано в виде равенства
t
V (х(Т)) = V (х(0)) + У* (y(s)T u(s) g^^ds, (4.5)
о
функция д(х) 0 называется скоростью диссипации (dissipation rate).
Как и в предыдущей главе, будем более подробно рассматривать гамильтоновы системы, линейные по входам. Для линейных по входам гамильтоновых систем с диссипацией, задаваемых гамильтонианом Н(q,p, u) = H₀(q,p) + #i(q,p)u естественной функцией запаса является энергия свободной системы: V(х) = H₀(q,p). При наличии диссипации скорость изменения энергии имеет следующее выражение:
H₀ = {H₀,H_l}u-R(q,p)T^.
Вводя обозначение д(х) = R(q, p)T(dH₀/dp) 0, получим, что соотношение (4.5) выполнено при у = {Н₀,Н₁}, Таким образом, есте-ственньш выходом системы, отражающим ее диссипативные свойства, является вектор у = {Н₀, Н₁}, представляющий собой вектор скоростей изменения гамильтонианов взаимодействия Н₁ вдоль траекторий свободной (при и = 0) системы (4.3). В частности, лагран-жева система (3.18) пассивна по отношению к вектору выходов, компонентами которого являются обобщенные скорости системы.

Этот факт широко используется в современной теории управления физическими системами [189, 190, 191, 217].
Отметим сходство и различие понятий функции запаса и функции Ляпунова. Наличие диссипации в физической системе тесно связано с ее устойчивостью. Действительно, легко видеть, что если х = 0 равновесие системы (4.3) при и = 0 (т. е. F(0,0) = 0), а функция запаса V(х) непрерывна и положительно определена (V(х) 0 при х = 0 ), то при отсутствии входных воздействий (и = 0) пассивная система устойчива по Ляпунову, а строго пассивная система асимптотически устойчива. При этом в качестве функции Ляпунова, устанавливающей устойчивость, выступает сама функция запаса V(х).

Однако неравенства диссипации (4.4) и (4.5) относятся и к случаю и = 0, позволяя исследовать зависимость поведения системы от входных воздействий. Таким образом, понятие функции запаса заменяет понятие функции Ляпунова при переходе от замкнутых систем к открытым (разомкнутым).

Индекс возбудимости

Для анализа возможности изменения характеристик системы за счет управления необходимо ввести количественную меру пределов такого изменения. Подобная мера зависит от выбора входа и выхода системы, а также от допустимой величины управляющего воздействия. Для определенности будем рассматривать в качестве выхода характеристику типа энергии функцию запаса V(х), а измерять величину входа будем по его уровню максимальному по времени значению, т. е. в равномерной норме.

При наличии диссипации величина V(х(Т)) в отсутствии управления имеет тенденцию к убыванию. Поэтому важное значение имеет величина, характеризующая возможность увеличения V(х) за счет управления. Такая величина определяет меру возбудимости движений (колебаний) в системе и
может быть названа индексом возбудимости.
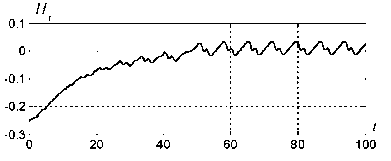
Для определения индекса возбудимости следует вычислять максимальное значение V(х), достижимое при ограниченном управлении в асимптотике, т.е. при t ^ ю. Однако вычислительные эксперименты показывают, что предел при t ^ ю может не существовать (см.напр. Рис.4.1, где показан характер изменения энергии маятника с трением при воздействии управления вида и = у sign ф), Поэтому необходимо рассматривать верхний и нижний пределы.

Введем следующее определение.
Определение 4.2. Пусть множество допустимых управлений состоит из функций и(Т), ограниченных при 0 t ю и таких, что соответствующие им траектории x(t) ограничены. Верхним и нижним индексами возбудимости системы (4.3) по отношению к выходу V(х) называются функции x+(y), X- (y), определенные при О y ю следующим образом:
Х?Ь) = ,lim sup V(x(t)), (4.6)
Т^Ж \u{-)\y x(0)=0
Xy(7) = ІІШ. sup V{x(t)). (4.7)
t-00 |u(-)|7
x(0)=0
?
Аналогичным образом определяются индексы возбудимости x+(y), X-(y) по отношению к любому выходу у = h(x). В случае, если вход является вектором, и = col{u₁,...,u_OT} величина входа также задается вектором y = {Y₁,...,Ym} и индексы возбудимости являются

Рис. 4.1. Динамика энергии маятника с трением Jф + дф + mgl sin ф = и при возбуждении управлением и = y sign ф.
мультииндексами. В общем случае системы с т входами и I выходами индексы возбудимости x+(y), X-(y) являются I х м-матрицами, зависящими от т аргументов.

Однако скалярные индексы возбудимости от входа і к выходу / также представляют интерес. Отметим, что предположение об ограниченности x(t) носит технический характер и может быть ослаблено, но здесь для простоты изложения этого не делается.
Индекс возбудимости может быть измерен экспериментально, как и обычная частотная характеристика линейной системы. В отличие от измерения частотной характеристики, когда на вход системы подается гармоническое воздействие (4.28) с постоянной амплитудой и меняющейся частотой, при измерении характеристики возбудимости меняется амплитуда (уровень) входного сигнала, а сам сигнал задается в виде обратной связи.
Основным результатом настоящего пункта является следующее утверждение.
Теорема 4.1. Пустъ система (4.3) пассивна, причем функция запаса V(х) и скорость диссипации q(x) удовлетворяют неравенствам
ао\у\2 V(х) а\у\2 + D, (4.8)
Qo|у|2 q(x) Qi|у|2 (4.9)
для некоторых положительных а₀, а₁, q₀, q₁, D. Пустъ множество
П~ = lx: h{x) = 0, ?(х) а₀ f 1
не содержит целых траекторий свободной системы X = F(х, 0).
Тогда индексы возбудимости x+(y), X- (y) по отношению к V(х) удовлетворяют неравенствам
OLо j Ху(y) Xy(Y) та\ + d, (4.10)
/ \ 2 / \ 2
а индексы возбудимости х+ (y), X- (y) по отношению к у удовлетворяют неравенствам
х_у (y) x^(y) (таі)1/2 +
Qo
1
Qi

При этом нижняя оценка реализуется для
(4.12)
u{t) = у sign у(Т).
Доказательство теоремы 4.1. Продифференцировав тождество (4.5) по t и воспользовавшись неравенствами (4.9), получим
УТи - Qi\у\2 V уТи - go\y\2 (4.13)

Содержание раздела

---