Синхронизация и адаптивные наблюдатели
Лемма 5.1 (Лемма о пассификации) [61, 78, 80]. Пусть заданы матрицы А, В, С, g размеров п х п, п х м, I х п, м х I и выполнено условие rank(B) = м. Тогда для существования положительно определенной п х n-матрицы Р = Рт 0 и I х м-матрицы в* таких, что
РА* + А*Р 0, РВ = СтgT, А* = А + В0*GC
необходимо и достаточно, чтобы система X = А х + В и, у = GC х была гипер-минимально-фазовой.
Из леммы следует [61], что для гипер-минимально-фазовой системы всегда существует обратная связь по выходу и = 0oGy + С, где С новый, вспомогательный вход, такая, что система с обратной связью строго пассивна по отношению к выходу у = Gy, причем функция запаса может быть выбрана в виде квадратичной формы: V(х) = х Px. Другими словами, гипер-минимально-фазовость необходима и достаточна для пассифицируемости линейной системы обратной связью по выходу.
Определение 5.4. Вектор-функция f : [0, то) ^ Rm называется постоянно возбуждающей (ПВ) на [0, то) , если она измерима и ограничена на [0, то) и существуют а 0, Т 0 такие, что
t+r
J f (s)f (s)Tds alm
t
для всех t 0. ?.
Постоянно возбуждающая вектор-функция отличается тем, что при t ^ то она не прижимается ни к какой гиперплоскости в m-мерном пространстве.
Лемма 5.2 (Лемма о постоянном возбуждении) [61, 78]. Рассмотрим вектор-функции f , ? : [0, то) ^ Rm.
Предположим, что ?(Т) непрерывно-дифференцируема, dO(t)/dt ^ 0 при Т ^ то и f - постоянно возбуждающая. Тогда, если B(t)1f(Т) ^ 0 при Т ^ то, то
?(Т) 0.
Условия адаптивной синхронизации сформулируем в виде следующей теоремы.
Теорема 5.1 [136]. Предположим, что траектории синхронизируемых систем с управлением вида (5.56) при ограниченных e(t), ?і(Т) ограничены и линейная система с передаточной функцией W(А) = gC(XI А)-1 В гипер-минимально-фазовая.
Тогда все траектории системы (5.55), (5.56),(5.59), (5.60) ограничены и выполнена цель синхронизации (5.54). Если, кроме того, условие ПВ выполнено для вектор-функции (р1(х1, х2, Т),..., pN(х1, х2, Т)), то настраиваемые параметры сходятся к своим идеальным значениям:
lim (?(Т) ?) =0. (5.63)
t-oo v
Доказательство теоремы 5.1. Для доказательства рассмотрим
функцию Ляпунова вида
ГГРе + Ё
V (х,?о,?)
?,|2 + |?о - ?,о|2/(27о)(5.64)
і=0
где матрица Р = Рт 0 и число ?*0 подлежат определению. Вычисление V показывает, что соотношение V 0 при е = 0 имеет место тогда и только тогда, когда выполнены следующие условия:
(5.65)
?о = Yo eTPBgCe,
?і = YieTPBpi(хі, X2, t),
причем матрица P удовлетворяет неравенству Ляпунова РА* + А*Р 0, где А* = А + В?0С. Вспоминая, что измеряемость всех величин, входящих в алгоритм адаптации эквивалентна выполнению соотношения РВ = С g, и применяя лемму 5.1, получим, что V 0 при е = 0 тогда и только тогда, когда алгоритм адаптации имеет вид (5.59), (5.60) и система X = Ах + Ви, у = gCx является гипер-минимально-фазовой, что, по условию, имеет место.
Поэтому функция V(Т) = V(х(Т), ?0(Т), ?(Т)) ограничена. Следовательно, ограничены также функции е(Т), ?,(Т) (так как у,(х1, х2, Т), і = 1, ...,N ограничены).
Из уравнений (5.65) следует, что V = ет(РА* +А*Р)е u|e(t)|2 для некоторого у 0. Теперь мы находимся в условиях леммы о частичной аттрактивности п. 3.1, где функция V имеет вид (5.64). Поскольку из ограниченности функции V(Т) следует ограниченность всех переменных состояния системы.
Из леммы следует, что е(Т) ^ 0 при t ^ж.
Для доказательства (5.63) заметим сначала, что из (5.54) и (5.59) следует, что ?(Т) ^ 0 при t -^ж. Дифференцированием (5.55), из ограниченности функций е, ?, , у, ?0 и их производных по времени заключаем, что ё(Т) ограничено. Из леммы Барбалата [61] следует, что ё(Т) ^ 0 при t ^ ж. Отсюда и из (5.59) получим, что ?(Т)Т(t) ^ 0 при Т ^ ж. Наконец, (5.63) следует из условия ПВ и леммы 5.2. ¦
Замечание 5.6. Теорема 5.1 фактически дает необходимое и достаточное условие существования функции Ляпунова вида (5.64)
со свойствами
(5.66)
V(х, ?0, ?, t) 0 при е = 0, ?(х, ?0, ?, t) 0 при е = 0.
Это означает, что нет другого алгоритма адаптации, основанного на функции Ляпунова (5.64) со свойствами (5.66). ?
Синхронизация и адаптивные наблюдатели
Аналогично задаче об адаптивном управлении синхронизацией рассматривается задача о синхронизации на основе адаптивного наблюдателя [6, 137], в которой модель неуправляемой системы (передатчика) имеет вид
N
Xd = Axd + V0(Yd) + в ^2 ?і Pi (Yd), Yd = Cxd, (5.67)
i=i
где xd e - вектор состояния передатчика; yd E Rl - вектор выходов (передаваемых сигналов); ? = col (?1,..., ?N) - вектор параметров передатчика. Предполагается, что нелинейности рі(- ), і = 0,1, ...,N, матрицы А, С и вектор В известны.
Задача состоит в построении адаптивного наблюдателя (приемника) динамической системы с входом yd(Т), вектор выходов которой w(t) состоит из оценок состояния передатчика Х(Т) и оценок параметров передатчика ?, обеспечивающего цель наблюдения - сходимость к нулю ошибок оценивания:
lim (Х(Т) - Xd(Т)) = 0, (5.68)
Т^х
lim (?(Т) - ?) =0. (5.69)
Адаптивный наблюдатель строится в виде
N
х = Ах + P0(yd) + В ( ^2 ?іPi(yd) + ?0G(yd у)^ ,
і=1
? = Фі (Yd , у), і = 0,1,..., N, (5.71)
где х g Rn,yd G Rl, ?і g R, a G g Rl является вектором весовых коэффициентов. Алгоритм адаптации (5.71) подлежит определению. Хотя формально задача наблюдения не является задачей управления, уравнение ошибки имеет как и ранее, вид (5.55), если ввести обозначения
N
Е = Xd - X, pi = Pi (yd), и = -0o(yd - CX) + ^ ?і Pi (yd).
i=i
Алгоритм адаптации, синтезированный методом скоростного градиента, имеет вид:
(?і = -Yi(у - Yd)Pi(Yd), i = 1, ...,N, (5.72)
?о = -Yo(y - Yd)2, (5.73)
где Yi 0.
Аналогично теореме 5.1 доказывается следующее утверждение, дающее условия адаптивной синхронизации:
Теорема 5.2 [6, 137]. Предположим, что все траектории системы (5.67) ограничены и линейная система с передаточной функцией W(Л) = С(XI - А)-1 В гипер-минимально-фазовая. Тогда все траектории системы (5.70), (5.72),(5.73), ограничены и выполнена цель наблюдения (5.68).
Если, кроме того, условие ПВ выполнено для вектор-функции (p1(yd(Т)),..., pN(yd(Т))), то выполнена цель наблюдения (5.69): настраиваемые параметры сходятся к своим идеальным значениям.
В работах [6, 137] было предложено применять адаптивный наблюдатель для передачи информации на основе хаотического несущего сигнала. При этом передаваемое сообщение кодируется изменением параметров ?і, і = 1,...,N. Преимуществом адаптивного приемника перед приемником, описанным в примере 5.7 является потенциально большая отказоустойчивость: отсеиваются нарушения синхронизации, не вызванные изменением параметров передатчика (например, внезапные сбои в передатчике или канале связи).
Исследование точности передачи сообщений в условиях ограниченных помех проведено в [7, 137].
Отметим, наконец, что для работы описанных схем адаптивной синхронизации существенна возможность пассификации уравнения ошибки, а значит, условие равенства единице относительной степени линейной части d = 1. В работе [138] предложены и обоснованы новые схемы адаптивной синхронизации на основе концепций расширенной ошибки и тюнеров высших порядков, позволяющие снять условие d = 1 за счет введения в структуру наблюдателя вспомогательных динамических систем фильтров.
Управление синхронизацией двух осцилляторов
Рассмотрим задачу синхронизации колебаний двух связанных одномерных осцилляторов с одной степенью свободы (например, математических маятников). Такая модель встречается при описании различных физических и механических систем (см., напр., [46]). В предположении линейности диссипации система из двух связанных осцилляторов описывается уравнениями
f p1(t) + gp1 + 40П'(p1(t)) = к(p2(t) p1(t)) + u(t), (5 74)
\ Ы0) + 9ф2 + 4П(Р2(Т)) = k(pi(T) P2(t)), .
где pi (t) (i = 1,2) - обобщенная координата і-го осциллятора (например, угол поворота маятника); u(t) - управляющее воздействие (например, приложенный к первому маятнику момент внешних сил, выраженный в единицах углового ускорения; и0 - частота малых собственных колебаний изолированных осцилляторов; д - коэффициент трения (диссипации); k - коэффициент связи (например, коэффициент жесткости пружины).
Введем вектор состояния системы x(t) = col {p1, 4, p2, ф2} ? R4. Полная энергия системы (5.74) Н(х) с учетом энергии связи определяется выражением
Н (х) = 0.5(?? + ^) + (П(Р1) П(р2)) + 0.5 k(p2 P1 )2. (5.75)
Рассмотрим задачу возбуждения синхронных антифазных колебаний осцилляторов с заданной амплитудой с помощью дополнительной ограниченной обратной связи. Эту задачу можно трактовать как достижение заданного уровня энергии системы с дополнительным требованием того, чтобы осцилляторы имели противоположные фазы колебаний.
Синтез алгоритма управления выполним по методу скоростного градиента.
Для применения процедуры метода скоростного градиента введем целевые функции
Qp(pi, Ф2) = 0.5 у,
Qh(х) = 0.5(Н(х) - Я*)2,
где 5Ф = фі + ф^2; Я (x(t)) - полная энергия системы, Я * - ее заданное значение.
Минимальное значение функции Qф соответствует требованию противофазности колебаний (во всяком случае при малых начальных фазах ф1(0), p2(0) тождество Qp(pb ф2) = 0 выполняется только тогда, когда ф1 = ф2). Минимизация QH означает достижение желаемой амплитуды колебаний.
Для синтеза алгоритма управления введем целевую функцию Q(х) как взвешенную сумму Qp и QH, а именно
Q(х) = aQp( ?1, ?2) + (1 a)QH(х), (5.77)
где а (0 а 1) - заданный весовой коэффициент.
Вычисляя скоростной градиент, получаем следующий алгоритм управления:
u(t) = Y (абф(t) + (1 а)^н(t)) ?i(t), (5.78)
где 5ф(t) = ?1(t) + ?2(t), 5Н(t) = Ht Я*, у 0 - коэффициент усиления. Результаты [6, 140, 220] к данной задаче, к сожалению, непосредственно не применимы, поскольку величина 5Ф не является инвариантом системы даже при д = 0 (она сохраняет свое значение на движениях свободной системы только на целевом множестве).
Поэтому проблема аналитического исследования достижения цели в системе (5.74), (5.78) остается открытым. В то же время вычислительные эксперименты убеждают в работоспособности алгоритма синхронизации (5.78).
Приведем некоторые результаты моделирования процесса возбуждения и синхронизации колебаний по алгоритму (5.78) в системе из двух одинаковых маятников. При моделировании использованы следующие значения параметров; k = 5, = 0.4л, у = 0.8, а = 0.7, Н* = 4.0.
Все начальные условия приняты нулевыми, за исключением ^2(0) = 0.05л.
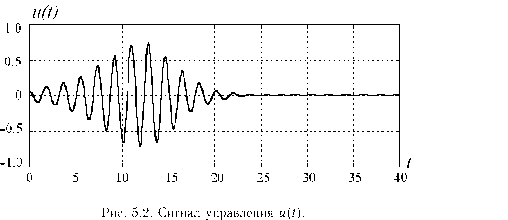
Рассмотрим сначала случай д = 0. Из приведенных на рис. 5.1
5.4 графиков видно, что после некоторого переходного процесса оба маятника совершают колебания с противоположными фазами и обе целевые функции приближаются к желаемым значениям. Время переходного процесса как для Нт, так и для Qv составляет около 20 ед. Соотношение между временем переходного процесса по Нт и по Qv можно изменить, изменяя коэффициент а. Амплитуда управляющего воздействия может быть произвольно уменьшена снижением коэффициента усиления у.
При наличии диссипации также удается достичь синхронизации маятников на заданном уровне энергии, но величина управления уже не может быть произвольно уменьшена. Из рис.
5.5, где представлены результаты моделирования для д = 0.05 видно, что при достижения того же уровня энергии Н* = 4.0 амплитуда управляющего воздействия устанавливается на уровне = lim^od^)! рз 0.5. Расчет по формуле (4.24) дает величину того же порядка, т. е. согласие теории и эксперимента достаточно хорошее.
Рис. 5.1.
Процесс возбуждения противофазных колебаний маятников.
Рис. 5.3.
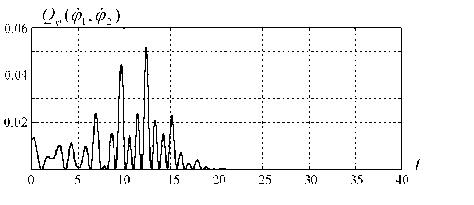
Динамика целевой функции синхронизации Q?(ф1(і), ф2(і)).
Рис. 5.5.
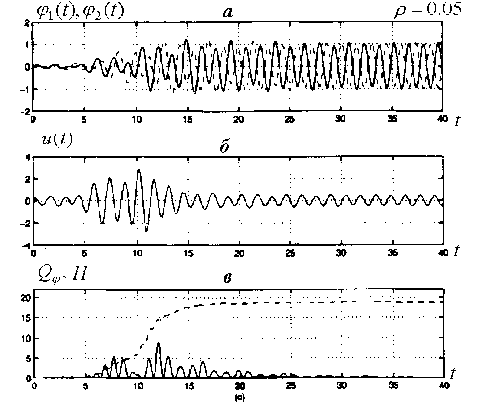
Процессы синхронизации при наличии диссипации.
Управление хаосом
Термин хаос происходит от греческого хама, означавшего в древнегреческой мифологии и философии беспорядочную смесь материальных элементов мира, из которой произошло все существующее. В современном языке термин употребляется для обозначения крайнего беспорядка, неразберихи, неорганизованности.
Поэтому сочетание управление хаосом имеет интригующий смысл и вызывает дополнительный интерес к предмету.
В научной литературе термин хаос, точнее детерминированный хаос, по-видимому, впервые был использован в 1975 г. в статье Т. Ли и Дж. Йорке Период три рождает хаос [175] и с тех пор широко употребляется. Известны различные математические определения хаоса, но все они выражают близкие по типу свойства динамических систем, связанные со сверхчувствительностью к начальным условиям: даже сколь угодно близкие траектории с течением времени расходятся на конечное расстояние, т. е. прогноз траектории на длительное время оказывается невозможен.
При этом каждая траектория остается ограниченной, что противоречит интуитивному пониманию неустойчивости, основанному на опыте работы с линейными системами.
Тем не менее оказалось, что нелинейные детерминированные системы с подобными свойствами встречаются достаточно часто. Оказалось также, что модели, описывающие хаотическое поведение, встречаются во многих областях науки и техники, и в ряде случаев являются более подходящим инструментом описания нерегулярных колебаний и неопределенности, чем стохастические, вероятностные модели.
Достаточно заметить, что широкий класс хаотических систем это хорошо известные генераторы псевдослучайных чисел.
Тем более удивительной оказалась обнаруженная в 1990 г. тем же Дж. Йорке с соавторами [192] возможность существенного изменения свойств хаотической системы при помощи весьма малого изменения ее параметров.
В частности, было показано путем компьютерного моделирования, что достаточно малым изменением параметра системы можно хаотическую траекторию преобразовать в периодическую и наоборот, если изменять параметр с учетом изменения текущего состояния системы, т. е. в контуре обратной связи.
В последующих публикациях эффект был подтвержден экспериментально [119] и указаны области его приложений: лазеры, системы связи, химические технологии, медицина (лечение аритмии и эпилепсии). Парадоксальность вывода (хаос нельзя прогнозировать, но им можно управлять) вызвала взрыв интереса исследователей и породила лавину публикаций, подтверждающих (как правило, путем компьютерного моделирования) возможность существенного изменения свойств разнообразных хаотических систем в природе и технике при помощи относительно небольших изменений параметров или внешних воздействий.
В настоящей главе приводятся краткие сведения об основных существующих методах управления хаотическими системами и о некоторых нерешенных задачах.
Что такое детерминированный хаос?
В течение нескольких десятилетий линейные модели колебаний и нелинейные модели с предельными циклами удовлетворяли потребности инженеров. Считалось, что они описывают все возможные типы колебаний детерминированных систем.
Это убеждение поддерживалось и математическими результатами: например, известная теорема Пуанкаре-Бендиксона утверждает, что единственно возможные виды ограниченных установившихся движений в непрерывных системах второго порядка - это либо состояние равновесия, либо предельный цикл.
Однако в середине XX века сами математики обнаружили, что уже для систем третьего порядка это не так: в системе становятся возможными весьма сложные движения - ограниченные непериодические колебания. Настоящий переворот начался с работы физика Е. Лоренца [180], опубликованной в 1963 г., где было показано, что качественный характер явлений атмосферной турбулентности, описываемых сложными уравнениями в частных производных Навье-Стокса, может быть передан простой нелинейной моделью третьего порядка (уравнение Лоренца):
Внимание физиков и математиков, а затем и инженеров к подобным моделям было привлечено после работы Д. Рюэля и Ф. Такенса [215], опубликованной в 1971 г., где такие аттракторы были названы странными, а также работы Т. Ли и Дж. Йорке [175], где был введен термин хаос для обозначения подобных нерегулярных явлений в детерминированных системах.
Основы математического аппарата для исследования хаотических явлений были заложены в 1960-1970-х годах отечественными научными школами: А.Н. Колмогоровым, В.И.
Арнольдом, Д.В.Аносовым, В.К.Мельниковым, Я.Г. Синаем, Ю.И. Неймар-ком, Л.П.
Шильниковым и их учениками.
В дальнейшем хаотическое поведение было обнаружено в огромном количестве систем в механике, лазерной физике и радиофизике, химии, биологии и медицине, в электронных цепях и т.д. Разработанные новые методы аналитического и численного исследования систем показали, что хаос - отнюдь не исключительный вид поведения нелинейной системы.
Грубо говоря, хаотические движения возникают, когда траектории системы глобально ограничены и локально неустойчивы. В хаотической системе сколь угодно малое начальное расхождение траекторий не остается малым, а в течение некоторого времени растет экспоненциально.
Частотный спектр хаотической траектории является непрерывным. Во многих случаях подобные нерегулярные, непериодические колебания лучше отражают свойства процессов, протекающих в реальных системах.
Свойство хаотичности движения по природе сложнее, чем, например, свойство устойчивости. Но даже для устойчивости существует несколько формально различных определений, каждое из которых подчеркивает какие-то свои особенности и оттенки.
Это делает математическую теорию устойчивости содержательнее и ближе к практическим задачам. Неудивительно, что и для хаотических систем существует несколько различных определений.
Приведем одно из простейших.
Рассмотрим динамическую систему в непрерывном времени
Х = F (х), (6.2)
где х = x(t) g Rn - вектор состояния системы, 0 Т ж.
Определение 6.1. Замкнутое множество О D Rn называется аттрактором системы (6.2), если О минимальное притягивающее множество, а именно: а) существует открытое множество Оо D О, такое что все траектории х(Т) системы (6.2), начинающиеся в Оо, определены при всех t 0 и стремятся к О при Т ^ ж; б) никакое собственное подмножество О этим свойством не обладает. ?
Определение 6.2. Аттрактор называется хаотическим, если он ограничен и любая траектория, начинающаяся на нем, неустойчива по Ляпунову. ?
Определение 6.3. Система называется хаотической, если у нее существует хотя бы один хаотический аттрактор. ?
Аналогичные определения даются для систем, дискретных по времени:
Хк+і = F (хк), К = 0,1,2,... (6.3)
Имеются и другие определения странных аттракторов и хаоса. Например, часто в определение странного аттрактора включают дополнительные требования: существование траекторий (или семейства периодических траекторий), всюду плотных в О, топологическую транзитивность и т.д., подчеркивающие наличие свойства перемешивания траекторий. Недавние результаты Г.А. Леонова [51] показывают, что вместо отсутствия устойчивости по Ляпунову при определении странного аттрактора целесообразно требовать отсутствия так называемой устойчивости по Жуковскому, допускающей разную скорость течения времени на разных траекториях системы.
Однако строго доказать хаотичность системы непросто, даже пользуясь простейшим определением. Поэтому основным методом изучения хаотических систем остается численное исследование - имитационное моделирование и оценка различных характеристик.
Неустойчивость характеризует основное свойство хаотических колебаний, называемое сверхчувствительностью, или чувствительной зависимостью от начальных условий: любые две сколь угодно
близкие траектории обязательно удаляются друг от друга на конечное расстояние.
Для задач управления могут оказаться существенными и другие свойства. В частности, важное значение имеет следующее свойство траекторий хаотических процессов, называемое рекуррентностью: со временем эти траектории попадают в сколь угодно малую окрестность своего положения в прошлом.
Рассмотрим это свойство подробнее.
Определение 6.4. Функция х : R1 ^ Rn называется рекуррентной (recurrent), если при любом е 0 существует такое Те 0, что для любого t 0 имеются Т(Т, е), 0 Т(Т, е) Те такие, что |х(Т + Т(Т, е)) - х(Т)| е.
Хаотический аттрактор является замыканием всех содержащихся в нем периодических траекторий. Понятие аттрактора связано и со следующим сформулированным Г. Биркгоффом в 1927 г. критерием рекуррентности: любая траектория, принадлежащая компактному минимальному инвариантному множеству является рекуррентной; любое компактное инвариантное множество является замыканием некоторой рекуррентной траектории.
При исследовании хаотических процессов и решении задач управления ими широкое применение нашли запаздывающие координаты и отображение Пуанкаре. Коснемся этих понятий.
Пусть у системы (6.2) доступна измерению только скалярная выходная координата y(t) = Н(х(Т)). Вектором запаздывающих координат (delayed coordinates) называется вектор-функция X(t) = \y(t), У(т-т),..., y(t-(N- 1)т)]т е Rn. Относительно этого вектора исходная модель системы (6.2) приводится к виду X = F(X(t)).
Из теорем вложения [29, 62, 64] следует, что если N 2п, где п порядок исходной системы (6.2), то в общем случае имеется диффеоморфизм между пространством состояний исходной системы и подпространством состояний преобразованной системы такой, что если исходная система имеет аттрактор некоторой размерности, то аттрактором такой же размерности будет обладать и преобразованная система.
Отображение Пуанкаре (Poincare тар), называемое также точечное отображение, отображение последования вводится в предположении, что имеется Т-периодическое решение Х(Т) уравнения (6.2), проходящее через некоторую точку x0 (т. е. x(t + Т) = x(t) для всех t to и x(t0) = x0). Пусть S гладкая поверхность, определяемая уравнением s(x) = 0, где 5 : Rn ^ R1 - гладкая скалярная функция. Предположим, что траектория трансверсально пересекает S в x0, т. е. выполнено s(x0) = 0, Vs(x0)TF(x0) = 0.
Можно показать, что решение, начинающееся в точке x е S = {x : 5(x) = 0} поблизости от точки x0 обязательно пересечет поверхность 5(x) = 0 хотя бы еще один раз. Пусть т = т(x) время первого возврата и x(t) е S точка первого возврата.
Перейдем к изложению методов управления хаотическими процессами, ограничиваясь процессами, протекающими непрерывно во времени.
Управление без обратной связи
Использование принципа управления без обратной связи, или управления по программе, т. е. формирование сигнала управления в виде некоторой функции времени без учета значений управляемого процесса, основано на изменении поведения нелинейной системы под воздействием заранее выбранного внешнего сигнала u(t). Этот сигнал может представлять собой либо определенное физическое воздействие на систему, например, внешнюю силу или поле, либо выражать изменение (модуляцию) некоторого параметра управляемой системы. Такой подход привлекателен простотой реализации, так как при нем не требуется проведения каких-либо измерений и установки датчиков.
Данное обстоятельство имеет особенное значение при управлении сверхбыстрыми процессами, происходящими, например на молекулярном или атомном уровне, для которых отсутствует возможность проведения измерений состояния системы (по крайней мере - в режиме реального времени).
