Однако если управление подается импульсами продолжительностью Т1 а промежутки между ними достаточно велики, то за время паузы между импульсами в ходе хаотического теплового движения некоторые молекулы приблизятся к состоянию х0, войдут в зону диссоциации и будут диссоциированы следующим управляющим импульсом. Если алгоритм достаточно грубый, робастный, то можно ожидать, что доля молекул, находящихся в зоне диссоциации, будет не слишком мала и процесс пойдет достаточно быстро.
Рассмотрим описанный подход более детально, следуя [88].
Примем классическое описание динамики отдельной молекулы в виде гамильтоновой модели (3.1). Роль координаты в (3.1) играет межатомное расстояние г(Т), а гамильтониан имеет вид
2
Н = і-I- П(г) - /і(г) и, (9.22)
2т
где т масса молекулы, П(г) потенциал межатомного взаимодействия, р(г) дипольный момент молекулы, и = и(Т) внешнее управляющее поле. Для описания межатомного взаимодействия будем использовать потенциал Морзе
П(г) = D (1 - е-а(г-а))2 - D = D (е-2Ыг-а) - 2е-а(г-а)) , (9.23)
где D - энергия связи, а - равновесное межатомное расстояние. Дипольный момент часто задают в форме [147, 235]
р(г) = Аге/л (г) = А (1 4?г4) ег, (9.24)
где А, ? - постоянные параметры. Если величина ?а4 мала по сравнению с единицей, то дипольный момент можно аппроксимировать линейной функцией: р(г) = Аг, (А(г) = А. При этом уравнения управляемой системы в лагранжевой форме примут вид
мГ = 2aD (е~2а(г~са) е~а(г~а) + Аи(Т). (9.25)
Такое описание предполагает, что движение молекулы одномерно, а ее ось ориентирована вдоль силовых линий управляющего внешнего поля, т.е. эффектами изменения ориентации и вращения молекулы пренебрегается.
Для формулировки цели управления заметим, что если полная энергия молекулы приближается к уровню П* = limr^TO П(г), то диссоциация становится все более вероятной. Очевидно, в случае потенциала Морзе (9.27) имеем П* = 0.
Выберем в качестве целевой функции квадрат отклонения энергии от желаемого значения Q(q,р) = 0.5(Ho(q,р) Н*)2, где
р2
H0(q,p) = j^ + Il(r)
- энергия свободной молекулы, Н* - заданная величина, близкая к порогу диссоциации П*. Вычислив скоростной градиент, как и ранее, придем к простым законам обратной связи
и = Е (Ho(q, р) Н*) Г, (9.26)
и = Е sign (Ho(q, р) Н*) sign Г, (9.27)
где Е 0; sign(H) = 1 при Н 0, sign(H) = 1 при Н 0 и sign(0) = 0.
В дальнейшем будем использовать упрощенный вариант алгоритма (9.27), полученный в предположении, что энергия молекулы всегда меньше порога диссоциации Н*:
и = Е sign Г . 185
Алгоритм (9.28) не требует точного знания порога диссоциации Н* и может применяться и для других задач, например для локализации молекулы в области повышенной энергии, так называемой предиссоциации.
Вычислительные эксперименты с системой (9.25), (9.28) проводились для числовых значений параметров, соответствующих молекуле фтористого водорода (HF) [147, 235]: м = 1732, D = 0.2101, а = 1.22, а = 1.75, А = 0.4541, ? = 0.0064, Е = 0.1. Значения указаны в атомных единицах Хартри (а.е.). Для расчета управляющего воздействия выбирались начальные условия вблизи равновесного состояния г = а, Г = 0 (эталонная молекула).
Интенсивность поля задавалась достаточно низкая: Е = 0.005 а.е. Результатом расчета являлась функция u(t),0 t Т1.
Рассчитанное управляющее воздействие u(t) подавалось на модель ансамбля, состоящего из N = 1000 молекул. Предполагалось, что молекулы не взаимодействуют друг с другом и с границей. Начальные условия для молекул ансамбля брались случайно и были распределены равномерно на поверхности заданного уровня энергии Н0 = 0.8689D.
Управление подавалось в виде повторяющихся импульсов с периодом повторения Т2, достаточно большим, чтобы дать возможность молекулам перемешаться за время паузы между импульсами. В экспериментах выбиралось Т2 = 200 Т0, где Т период малых колебаний молекулы вблизи равновесного положения. Мерой эффективности управления являлась доля диссоциировавших молекул (в процентах к общему числу молекул).
Под диссоциацией понималось превышение молекулой уровня энергии Н* = 0.1185D. Поскольку значение Н* занижено по сравнению с порогом диссоциации Н* = 0, точнее называть это состояние предиссоциацией.
Однако, учитывая, что целью исследования являлась принципиальная проверка работоспособности подхода, мы не будем в дальнейшем акцентировать на этом внимание.
Предложенный алгоритм сравнивался по эффективности со стан-дартньш алгоритмом чирпинга
u(t) = Е соб(Фо + Qot) (9.29)
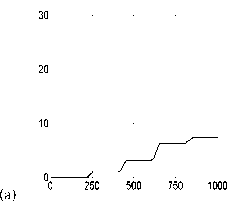
На рис. 9.17, а представлена зависимость доли диссоциировавших молекул от времени при управлении линейно чирпированным полем. Скорость чирпа е (скорость изменения несущей частоты импульсов) подбиралась экспериментально для достижения наибольшей доли диссоциировавших молекул и в эксперименте была е = 0.0Ш0/70.
На рис. 9.17, Б представлена аналогичная зависимость для алгоритма скоростного градиента.
Из рисунков видно, что эффективность последнего в несколько раз выше эффективности линейного чирпинга. Важно, что система с чирпингом весьма чувствительна к величине скорости чирпа е. Подбор параметра е требует значительного объема вычислений и значительно более точного знания параметров молекулярного гамильтониана и дипольного момента, чем требуется для эффективной работы алгоритма (9.28).
Интересным и до сих пор вызывающим дискуссии является вопрос о правомерности использования классических представлений при моделировании и управлении молекулярными процессами. Динамика двухатомной молекулы более адекватно описывается вместо классической модели (9.25) квантово-механической (точнее, полуклассической) моделью, представленной нестационарным уравнением Шредингера
дФ h2 д2 Ф
іН^і = ж^ + ЩФ + Агит' (9'30)
где Ф = Ф(^, г) волновая функция, квадрат модуля которой определяет плотность вероятности нахождения молекулы в данном состоянии; П(г) потенциал Морзе (9.23). Вероятность диссоциации (доля диссоциировавших молекул) определяется как вероятность состояний с энергией, превышающей порог диссоциации И*.
Однако классические вычисления во многих случаях дают результат, достаточно близкий к реальности. Поэтому было проведено численное сравнение результатов моделирования процессов управляемой диссоциации в классической и квантовой постановках.
Для численного анализа квантовой модели (9.30) была построена конечно-уровневая аппроксимация модели путем разложения решения по собственным функциям невозмущенного уравнения Шредингера. Собственные значения и собственные функции невозмущенного оператора Шредингера для потенциала Морзе могут быть вычислены аналитически [77]. Управляющее воздействие и время моделирования были взяты такими же, как и в классическом случае.
Начальное состояние системы было выбрано как чистое состояние с энергией, равной второму энергетическому уровню, а порог диссоциации И* соответствовал пятнадцатому энергетическому уровню молекулы HF, что также соответствует классическому случаю.
Результаты квантово-механического моделирования представлены на рис. 9.18.
Видно, что алгоритм скоростного градиента обеспечивает вероятность диссоциации 14% после 5 импульсов, что существенно превышает вероятность диссоциации для чирпированного импульса и согласуется с результатами для классического случая (10 - 12%).
В основе традиционного спектроскопического исследования лежит воздействие на исследуемую систему гармоническим внешним сигналом (монохроматическим излучением). Оценка возможных энергетических уровней и выбор вектора состояния модели процесса делается на основе квантово-механических представлений (например, в лазерной спектроскопии используются модели динамики матрицы плотностей состояний квантового ансамбля [52]. Однако при расчете динамики резонансного взаимодействия вещества и излучения используется, как правило, классическая модель гармонического осциллятора [52]).
Реальная система имеет много степеней свободы и, соответственно, множество собственных режимов с различными собственными частотами и различными коэффициентами затухания (поглощения). Интерес представляют резонансные режимы, для которых поглощение малО.
Воздействие с частотой, близкой к резонансной, соответствует пику (линии) спектрограммы.


Управляемая диссоциация в классическом ансамбле а) линейно чирпированные импульсы, б) импульсы, рассчитанные по методу скоростного градиента. Доля диссоциировавших молекул указана в процентах, время в единицах То.
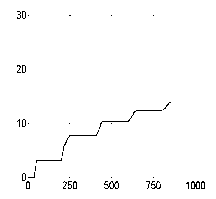
Вероятность диссоциации при квантово-механическом моделировании для Е = 0.005 а.е.: а) линейно чирпированные импульсы, б) импульсы, рассчитанные по методу скоростного градиента. Вероятность диссоциации указана в процентах, время в единицах То.
Нелинейность динамики отклика системы обычно трактуется как возмущение модели (ангармоничность), меняющее условия резонанса. Если амплитуда колебаний возрастает и влияние нелинейности становится существенным, то часть энергии излучения не поглощается системой, а отражается или рассеивается.
В результате уровень энергии (4.30), соответствующий резонансу в линейном приближении в системе не достигается.
Ситуация меняется, если предположить, что внешнее воздействие может зависеть от состояния системы, т.е. может включать обратную связь. Даже если нелинейность существенна, воздействие вида (4.25) выводит систему на уровень энергии, не меньший, чем (4.31), порядок которого для слабодемпфированных систем совпадает с (4.30). Таким образом, возникает возможность более полного возбуждения системы и оценивания ее способности поглощать энергию на более высоких энергетических уровнях, а значит, повышения чувствительности метода. Понятно, что нелинейность играет существенную роль лишь при значительной амплитуде выходного сигнала.
Это условие выполняется в современной лазерной спектроскопии, где расчеты ведутся на основе нелинейных моделей, хотя и без учета обратных связей. Методы спектроскопического исследования, основанные на обратной связи, должны включать в себя традиционные методы, роль которых заключается в определении околорезонансных областей и начальном возбуждении системы.
В качестве обратной связи можно использовать простой закон (9.14), не требующий измерения энергии и не зависящий от формы потенциала, т.е. от формы ангармоничности.
Конечно, проблема реализации закона возбуждения с обратной связью далеко не проста, поскольку требуется измерение не только интенсивности, но и фазы возбуждаемых колебаний. Однако появление высокоскоростных управляемых лазеров, рост быстродействия и точности измерительной аппаратуры дают перспективу экспериментальной проверки подхода. Реализация обратной связи упрощается в областях, где частоты возбуждения сравнительно низки, например в виброакустике, ультразвуковой дефектоскопии.
В более высокочастотных диапазонах можно использовать частотно-модулированный тестовый сигнал, сравнение его с эталонным и введение обратной связи в диапазоне частот биений [82].
Современные физические исследования становятся все более ориентированы на запросы практики. Как следствие, понятие цели все чаще играет в них существенную роль. Этому способствует и грантовая система финансирования: для получения грантов нужна сильная мотивация; редкое исследование нынче выполняется из чистого любопытства. Наряду с прямыми задачами (задачами анализа) все чаще ставятся и задачи обратные (задачи синтеза), решение которых определяет, как достичь того или иного состояния системы.
Признаком этой тенденции является то, что термин управление все чаще появляется на страницах физических журналов. Неудивительно поэтому, что все чаще в физических работах применяются и методы современной теории управления, создавшей за полвека интенсивного развития мощный инструментарий для аналитического и численного решения задач синтеза в самых разнообразных ситуациях.
Выше были проанализированы основные особенности задач управления в физических системах и представлены общие подходы к решению задач управления фундаментальной характеристикой систем энергией. Установлены законы преобразования энергии для основных классов систем: консервативных и диссипативных.
Рассмотрен ряд других классов задач управления физическими системами. Новые постановки потребовали введения новых понятий (индекс возбудимости) и привели к описанию новых эффектов (резонанс с обратной связью).
Приведенные примеры показывают плодотворность новых подходов в исследовании и управлении явлениями макро- и микромира.
Из-за пространственно-временнЫх ограничений в книге не представлен целый ряд важных применений методов теории управления в физике. По мнению автора, будущий курс кибернетической физики не может не включать такие главы как оптимизационная термодинамика [99, 85], управление пучками частиц [66], теорию динамических материалов [101], исследование универсальных структурных свойств и робастности сложных физических систем [113] и ряд других. Нельзя не упомянуть о недавних работах по применению теории управления в других естественных науках (химия, биология), открывающих и в них новые горизонты [224, 225], а также о применениях других методов кибернетики (идентификация, распознавание образов, нейронные сети, оптимизация), которым посвящается все большее число статей в международных научных журналах.
К области кибернетической физики относится и одна из крупнейших нерешенных проблем, которые ХХ-й век передал веку ХХІ-му: проблема управляемого термоядерного синтеза. В целом, взгляд в будущее внушает оптимизм.
Интерес к новой области велик. Велика и тяга к общению работающих в ней исследователей, представляющих различные науки. Это показал успех прошедшей в Санкт-Петербурге в августе 2003 г. международной конференции Физика и управление 2003 (Physcon 2003), в которой приняло участие около 250 специалистов из 32 стран.
Материалы конференции, в том числе новые результаты лидеров мировой науки представлены в четырех томах трудов [202] [205] общим объемом около 1500 стр.
Автор надеется, что данная публикация также послужит дальнейшему развитию и признанию новой научной области.
1. Акуленко Л.Д. Гашение колебаний системы, содержащий неуравновешенный ротор // Изв. РАН.
Механика твердого тела. 1993.
С. 110-118.
2. Алексеев В.В., Лоскутов А.Ю. Дестохастизация системы со странным аттрактором посредством параметрического воздействия // Вестн. МГУ. сер.З, Физика, астрономия.
1985, Т. 26, 3, С. 40-44.
3. Алексеев В.В., Лоскутов А.Ю. Управление системой со странным аттрактором посредством периодического параметрического воздействия // ДАН СССР, 1987, Т. 293, 6, С. 1346-1348.
4. Андриевский Б.Р., Гузенко П.Ю., Фрадков А.Л. Управление колебаниями механических систем методом скоростного градиента // Автоматика и телемеханика.
1996. 4. С. 4-17.
5. Андриевский Б.Р., Стоцкий А.А., Фрадков А.Л. Алгоритмы скоростного градиента в задачах адаптации и управления // Автоматика и телемеханика.
1988. 12.
С. 3-39.
6. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке MATLAB.
СПб.: Наука, 1999. 467 с.
7. Андриевский Б.Р., Фрадков А.Л. Элементы математического моделирования в программных средах MATLAB 5 и Scilab.
СПб.: Наука, 2001.
8. Андриевский Б.Р., Фрадков А.Л. Управление хаосом: Методы и приложения.
I. Методы // Автоматика и телемеханика. 2003.
5. С. 345.
9. Андриевский Б.Р., Фрадков А.Л. Управление хаосом: Методы и приложения. II.
Приложения // Автоматика и телемеханика. 2004. 4.
10. Афанасьев М.М., Блехман И.И., Макаров В.А., Печенев А.В.
Динамика системы принудительной синхронизации механических вибровозбудителей с асинхронным приводом // Машиноведение. 1983.
4, С. 3-11.
11. Афраймович В.С., Веричев Н.Н., Рабинович М.И.
Стохастическая синхронизация колебаний в диссипативных системах // Изв. вузов. Радиофизика. 1986. Т. 29.
9, С. 1050-1060.
12. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. 2-е изд.
М.: Физматгиз, 1959.
13. Беллман Р., Дрейфус С. Прикладные методы динамического программирования.
М.: Физматлит, 1965.
14. Блехмаи И.И.
Синхронизация динамических систем, М.: Наука, 1971. 894 с.
15. Блехмаи И.И.
Вибрационная механика. М.: Наука, 1994.
16. Бриллюэи Л. Наука и теория информации.
М.: Физматгиз, 1960.
17. Бутковский А.Г.
Теория оптимального управления системами с распределенными параметрами. М.: Наука, 1965.
18. Бутковский А.Г. Методы управления системами с распределенными параметрами.
М.: Наука, 1975.
19. Бутковский А.Г., Самойлеико Ю.И.
Управление квантовомеханическими процессами. М.: Наука, 1984, 256с. (English
translation: Dordrecht: Kluwer Academic Publishers, 1990).
20. Валиев K.A., Кокии A.A.
Квантовый компьютер: мечта или реальность? Ижевск: Регулярная и хаотическая динамика, 2000.
21. Вииер Н. Кибернетика.
2-е изд. М.: Сов. радио, 1968.
22. Воротников В.И., Румянцев В.В.
Устойчивость и управление по части координат фазового вектора динамических систем: теория, методы и приложения. М.: Научный мир, 2001. 320 с.
23. Галилей Г. Избранные труды, т. 1-2, М.: Физматгиз, 1964.
24. Глеисдорф П., Пригожии И. Термодинамическая теория структуры, устойчивости и флуктуаций.
М.: Мир, 1973.
25. Гольмаи Е.К., Гольдрии В.И., Плоткии Д.А., Разумов С.В., Кукушкин С.А., Осипов А.В.
Самоорганизация при зарождении пленок в системе высокотемпературного сверхпроводника Y-Ba-Cu-О //Физика твердого тела. 1997.
Т. 39, 2. С. 216-219.
26. Гордеев С.К., Гузенко П.Ю., Кукушкин С.А., Осипов А.В., Фрадков А.Л. Влияние нелинейных реакций синтеза углерода на зарождение пор в углеродных наноматериалах // Журнал физической химии. 2003.
Т. 77, 10, С. 1893-1895.
27. Гузеико П.Ю. Дискретное управление непрерывными хаотическими системами // Анализ и управление нелинейными колебательными системами / Под ред. Г.А.
Леонова, А.Л. Фрадкова. СПб.: Наука, 1998.
С. 53-84.
28. Гузеико П.Ю.,Кукушкии С.А.,Осипов А.В.,Фрадков А.Л. Автоколебательные режимы роста тонких пленок из многокомпонентного пара: динамика и управление // Журнал технической физики. 1997.
Т. 67. 9. С. 47-51.
29. Гукеихеймер Дж., Ф. Холмс.
Нелинейные колебания, динамические системы и бифуркации векторных полей. М.: Изд-во УРСС, 2002.
30. Гуртовиик А.С., Неймарк Ю.И. О синхронизации динамических систем // Прикл. матем. механика. 1974.
Т. 38, 5. С. 799-809.
31. Демидович Б.П. Лекции по математической теории устойчивости. М.: Наука, 1967; 2-е изд.
МГУ, 1998.
32. Дмитриев А.С., Панас А.И., Старков С.О. Динамический хаос как парадигма современных систем связи //Зарубежная радиоэлектроника.
1997. 10.
С. 4 - 26.
33. Дудник Е.Н., Кузнецов Ю.И., Минакова И.И., Романовский Ю.М. Синхронизация в системах со странным аттрактором // Вестн.
МГУ. Сер. 3: Физика.
Астрономия. 1983.
Т. 24, 4. С. 84-87.
34. Емельянов И.Я., Ефанов А.И., Константинов Л.В.
Научнотехнические основы управления ядерными реакторами. М.: Энерго-атомиздат, 1981.
35. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику: От маятника до турбулентности и хаоса.
М.: Наука, 1988.
36. Кадомцев Б.Б.
Динамика и информация. 2-е изд. М.: Редакция журнала Успехи физ.наук.
1999.
37. Калман Р. Фалб П., Арбиб М. Очерки по математической теории систем.
М.: Мир, 1971.
38. Капица П.Л.
Динамическая устойчивость маятника при колеблющейся точке подвеса // ЖЭТФ. 1951.
Т.21. N 5.
39. Кафаров В.В.
Методы кибернетики в химии и химической технологии. М.: Химия. 1976. (4-е изд.
1985. 448с.)
40. Квантовый компьютер и квантовые вычисления.
Т. 2. Ижевск: Регулярная и хаотическая динамика, 1999.
41. Ковалева А.С. Асимптотическое решение задачи оптимального управления нелинейными колебаниями в окрестности резонанса // Прикладная математика и механика. 1998.
Т. 62, вып. 6. С. 913-922.
42. Колесников А.А. Основы теории синергетического управления.
М.: Испо-Сервис, 2000.
43. Красносельский А.М. О возникновении колебаний с большой амплитудой в системах с насыщением // Докл. АН СССР.
1991. Т. 318, 4. С. 844-848.
44. Крутько П.Д. Управление колебаниями. Синтез алгоритмов на основе обращения прямого метода Ляпунова // Известия РАН.
Теория и системы управления. 2003. 2.
45. Кукушкин С.А., Осипов А.В. Самоорганизация при зарождении многокомпонентных пленок //Физика твердого тела.
1995. Т. 37, 7. С.2127-2132.
46. Ланда П.С.
Нелинейные колебания и волны. М.: Наука, Физматлит, 1997. 496 с.
47. Ландау Л.Д., Лифшиц Е.М.
Механика. М.: Наука.
48. Ландау Л.Д., Лифтиц Е.М. Статистическая физика.
М.: Наука.
49. Ланцот К. Вариационные принципы механики.
М.: Физматлит, 1965.
50. Леонов Г.А., Смирнова В.Б. Математические проблемы теории фазовой синхронизации.
СПб.: Наука, 2000.
51. Леонов Г.А., Шумафов М.М.
Проблемы стабилизации линейных управляемых систем. СПб.: СПбГУ, 2002.
52. Летохов В.С., Чеботаев В.П. Нелинейная лазерная спектроскопия сверхвысокого разрешения.
М.: Наука, 1990.
53. Линдсей В. Системы синхронизации в связи и управлении.
М.: Мир, 1978.
54. Лоскутов А.Ю. Проблемы нелинейной динамики.
II. Подавление хаоса и управление динамическими системами // Вестн. МГУ.
2001. 2. С. 3-21.
55. Магницкий Н.А., Сидоров С.В. Управление хаосом в нелинейных динамических системах // Дифференциальные уравнения.
1998. 11.
С. 1501-1509.
56. Магницкий Н.А., Сидоров С.В.
Некоторые подходы к управлению диффузионным хаосом // Дифференциальные уравнения. 1999.
Т. 35, 5. С. 669-674.
57. Мирзоев Ф.Х., Панченко В.Я., Шелепин Л.А. Лазерное управление процессами в твердом теле // Успехи физ. наук.
Т. 166, 1. С. 3-32.
58. Миронова В.А., Амелькин С.А., Цирлин А.М. Математические методы термодинамики при конечном времени.
М.: Химия, 2000.
59. Миротник И.В., Ушаков А.В. Синтез алгоритма синхронного управления квазиподобными системами // Автоматика и телемеханика. 1977, 11.
С. 22-29.
60. Миротник И.В. Согласованное управление многоканальными системами.
Л.: Энергоатомиздат, 1990.
61. Миротник И.В., Никифоров В.О., Фрадков А.Л. Нелинейное и адаптивное управление сложными динамическими системами.
СПб.: Наука, 2000.
62. Мун Ф. Хаотические колебания.
М.: Мир, 1990.
63. Налимов В.В., Маркова Е.В. Химическая кибернетика // Информационные материалы Научного совета по комплексной проблеме Кибернетика АН СССР. 1970.
11-12. С. 105-127.
64. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания.
М.: Наука, 1987. 424 с.
65. Николис Г., Пригожин И. Самоорганизация в неравновесных системах.
М.: Мир, 1979.
66. Овсянников Д.А.
Математические методы управления пучками. Л.: Изд-во ЛГУ, 1980.
67. Планк М. Принцип наименьшего действия // Единство физической картины мира.
М.: Наука, 1966.
68. Полушин И.Г., Фрадков А.Л., Хилл Д. Пассивность и пассификация в теории нелинейных систем // Автоматика и телемеханика. 2000.
3. С. 3-37.
69. Первозванский А.А.
Курс теории автоматического управления: Учебное пособие. М.: Наука, 1986. 615 с.
70. Пиковский А.Б., Розенблюм М.Б., Курте Ю. Синхронизация.
Фундаментальное нелинейное явление. М.: Техносфера, 2003.
71. Поплавский Р.П.
Термодинамика информационных процессов. М.: Наука, 1981.
72. Румянцев В.В.
Об оптимальной стабилизации управляемых систем // ПММ. 1970.
Т. 34, вып. 3. С. 440-456.
73. Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ.
М.: Наука. 1978. 352 с.
74. Турчин В.Ф. Феномен науки: Кибернетический подход к эволюции // Изд.
2-е. М.: ЭТС.
2000. 368 с.
75. Управление мехатронными вибрационными установками / Под ред. И.И. Блехмана, А.Л.
Фрадкова. СПб.: Наука, 2001. 278 с.
76. Управление молекулярными и квантовыми системами / Под ред.
А.Л. Фрадкова, О.А.Якубовского.
Москва-Ижевск: Регулярная и хаотическая динамика, 2003. 410 с.
77. Флюгге 3. Задачи по квантовой механике. т. І,ІІ.
М.: Мир, 1974.
78. Фомин В.Н., Фрадков А.Л., Якубович В.А.
Адаптивное управление динамическими объектами.