Резонанс с обратной связью

Подставим в (4.13) функцию управления u(T) = у sign у(Т). Используя легко проверяемые оценки \у\ уТ sign у \fm\y\ и неравенства (4.8), имеем
V-d
аі
?_
ао
V \у\

\ у\
(4.14)
У - Qi
Заметим, что мы рассматриваем только ограниченные решения х(Т) и, значит, каждое из них имеет хотя бы одну предельную точку. Интегрируя полученное двойное дифференциальное неравенство относительно V_t = V(х(Т)), получаем, что предельные точки решений х(Т) могут содержаться в объединении множеств ?(х) а₀ ( ^

(4.15)
?(х) - ( у
- m (
а1 \Qo
только в случае, если Н(х(Т)) стремится к нулю при Т ж. Таким образом, если х* предельная точка для х(Т), то Н(х*) = 0. Точка х* не может принадлежать множеству О- в силу условия теоремы, а
множество 0+ = : h(x) = 0, ?(х) mai(^)2 + dj пусто, посколь
ку из (4.8) следует, что V(х) D при у = 0. Поэтому все предельные точки решений х(Т) должны содержаться в пересечении множеств
К)аШ 1’ ЧЧЧ) I’ (4Л6)
т. е. при достаточно больших Т 0 справедливы неравенства
+d.
Q0
1
Q1
(4.17)
а0
Заметим теперь, что правая часть дифференциального неравенства (4.14) является мажорантой для V не только при и = sign у, но и при любых других допустимых входах \щ (t)\, I = 1,..., т, t 0, удовлетворяющих ограничениям \щ(Т)\ у для всех t 0. Поэтому при интегрировании как левого, так и правого из неравенств (4.14) при каждом конечном t можно перейти в (4.17) к супремуму по множеству допустимых входов. Беря затем нижний и верхний пределы по t, получаем требуемые оценки (4.10), а затем и (4.11). ¦
Замечание 4.1. Если вместо неравенств (4.9) потребовать выполнение неравенств
Qo\y\ б(х) 61 \У\, (4.18)
соответствующих сухому трению, результат будет качественно иной: при у 6₁ индексы возбудимости бесконечны, а при у б₀ индексы возбудимости равны нулю (т. е. возбуждение колебаний невозможно). ?
Замечание 4.2. Закон управления (4.12), реализующий нижнюю границу индексов возбудимости, обладает высокой степенью робастности, поскольку он не зависит от параметров управляемой системы: функций потенциальной энергии, кинетической энергии и диссипации.

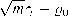
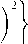
Закон (4.12)является также локально оптимальным. Он будет близок к оптимальному, реализующему супремум в (4.6),(4.7) при малых у 0 [84]. ?
Полученный результат применим к управляемым механическим системам, описываемым уравнениями в лагранжевой или гамильтоновой форме. Здесь в качестве функции запаса V(х) выступает полная энергия. Для лагранжевых систем она имеет вид Н(х) = \(fA(q)q + П(д), где q вектор обобщенных координат, у = q вектор обобщенных скоростей), х = (q, д), A(q) матрица кинетической энергии, n(q) потенциальная энергия. При этом выходом, по отношению к которому система пассивна, является вектор обобщенных скоростей у = д. Для гамильтоновых систем функция энергии имеет вид Н(х) = ^pTA~l(q)p + П(д), где q вектор обобщенных координат, р вектор обобщенных импульсов, х = col(q, р), а выходом, по отношению к которому система пассивна, является вектор у = A(q)p, т.е. снова вектор скоростей.

В обоих случаях неравенства (4.8) означают равномерную невырожденность и ограниченность матрицы кинетической энергии A(q) (стандартное предположение для механических систем), а также ограниченность функции потенциальной энергии. Неравенства (4.9) соответствуют вязкому трению, растущему со скоростью не быстрее, чем линейно.
Для определенности рассмотрим лагранжеву систему (3.18). Введем верхний и нижний индексы возбудимости Е + (у), Е-(у) следующим образом:
Е±( 7) = -у/^В, (4.19)
Y
где _
Х+(у) = lim sup H(q(t),q(t)), (4.20)
\u{-)\y
х(0)=0
Х_(7) = ІІШ_ SUP H(q(i),q(i)). (4.21)
t-00 |u(-)|7 x(0)=0
Следующий результат непосредственно вытекает из теоремы 4.1.
Теорема 4.2 [130]. Пустъ
0 а0 X, (A(q)) аі,
ео|q|2 R(q)Tq gi|q|2,
0 n(q) D,
где X,(A(q)) собственные числа матрицы A(q).
Тогда
у X~(l) X+(l) ma_x (^j + d. (4.22)
Если R(q) = gq и g 0, mo
?±(₇) ~ Д (4.23)
g
Замечание 4.3. Соотношения (4.22) и (4.23) можно трактовать как законы преобразования энергии ограниченным управлением для лагранжевых систем с диссипацией:
Для управляемой лаграижевой или гамильтоновой системы с малой диссипацией степени р уровень энергии, достижимой при помощи управления уровня у имеет порядок (у/р)2.
В частном случае системы с одной степенью свободы п =1, а₀ = а₁, Qo = Q₁ и полученные оценки упрощаются.
Пример 4.1. Рассмотрим вновь маятник из примера 3.1, в модели которого учтем трение с коэффициентом q. Из теоремы 4.2 получим оценку:
2
+ 2цу
2
77
(4.24)
0.5
Закон управления, реализующий оценку (4.24), имеет вид
(4.25) и = у sign(^).
Более точные оценки можно получить при дополнительном предположении о близости установившихся колебаний в замкнутой системе к гармоническим (это предположение верно при малых у). Например, для маятника метод гармонического баланса по средней энергии дает оценку согласующуюся с (4.24), поскольку 0.5 8/л2 1. ?

Приведенные оценки дают возможность оценить степень возбудимости и резонансные свойства нелинейных систем и получить дополнительную информацию об их динамических характеристиках.
Отметим, что для систем с диссипацией отбросить предположение (4.8) об ограниченности потенциала в теореме 4.1 не удается. Таким образом, вопрос о том, когда можно раскачать систему ограниченным управлением до сколь угодно больших уровней энергии, остается открытым для систем с полной диссипацией и неограниченным потенциалом (например, для системы Дуффинга, см. ниже).

Резонанс с обратной связью

Выше были описаны общие алгоритмы вывода системы на заданный уровень энергии и общие теоремы об их свойствах. Теперь на основе общих результатов мы установим некоторые свойства физических систем, выявляемые при помощи воздействия на них с обратной связью по измерениям.

Именно, изучим явление резонанса в системах с обратной связью.
Явление резонанса играет важнейшую роль в физике и технике, имея как полезные, так и вредные последствия. На принципе резонанса основана работа многих механических и электрических приборов, резонанс широко применяется в радиотехнике, акустике и лазерной технике.

Термин резонанс имеет итальянское происхождение и означает эхо. По-видимому, впервые явление резонанса было описано и изучено Галилео Галилеем, который в своем труде Диалоги и математические доказательства, касающиеся двух новых наук, опубликованном в 1638 г., писал [23]:
... маятник, находящийся в покое, хотя бы и очень тяжелый, мы можем привести в движение, и притом очень заметное простым дуновением, если мы будем приостанавливать дыхание при возвращении маятника, и вновь дуть в соответствующий его качанию момент.
Для колебательных систем резонансный режим означает возбуждение значительных колебаний системы при подаче малого воздействия и, значит, наиболее эффективную передачу энергии от возбуждающей системы к возбуждаемой. Закономерности резонанса хорошо изучены для линейных систем.

Однако для нелинейных колебательных систем дело обстоит сложнее. Даже само определение понятия резонанса неоднозначно и допускает различные варианты.

Рассмотрим этот вопрос подробнее.
Пусть управляемый нелинейный осциллятор с одной степенью свободы описывается уравнением
ф + П (ф) = и, (4.26)
где ф = ф(Т) скалярная фазовая координата; и = u(t) скалярное управляющее воздействие; П(ф) 0 потенциал. Состоянием
65
системы (4.26) является пара х = с?1{ф, ф}, а ее полная энергия имеет вид Н(р,ф) = \ф2 + П{(f). В силу консервативности свободной ( и = 0)системы все ее траектории лежат на энергетических поверхностях линиях постоянного уровня полной энергии {(ф, ф) : И(ф, ф) = И*}.

При различных значениях И* траектории обладают качественно различными свойствами: устойчивые и неустойчивые равновесия, гомоклинические и гетероклинические орбиты, неограниченные траектории (см., напр., [46] для случая маятника системы с потенциалом вида П(ф) = u0(1 _ cosф) ). Поставим вопрос: насколько можно изменить траекторию системы (4.26) при помощи сколь угодно малого внешнего воздействия u(t)?
Хорошо известно, что для случая квадратичного потенциала П(ф) = т^оф2, т. е. для гармонического осциллятора, описываемого линейным уравнением
ф + и2₀ф = и, (4.27)
гармоническое внешнее воздействие
u(t) = у sin ut (4.28)
при u = и₀ и сколь угодно малой амплитуде у позволяет наблюдать наличие неограниченных решений, например вида p(t) = ^ cos cut. Это явление и называется обычно резонансом.
Динамика нелинейных систем более сложна. Даже для простого маятника вынужденные колебания могут иметь сложный, нерегулярный характер [35, 46, 62, 64]. Известны работы, устанавливающие условия резонанса, например в смысле неограниченного роста нормы решений при приближении частоты воздействия к некоторому бифуркационному значению [43, 105].

Однако существующие результаты относятся лишь к задачам с периодическими решениями и не охватывают случай нерегулярных, в частности хаотических, движений.
Сложность создания и исследования резонансных режимов в нелинейных системах объясняется тем, что частота колебаний в них существенно зависит от амплитуды. Возникает естественная мысль: создавать колебания в нелинейной системе, варьируя частоту внешнего воздействия в зависимости от амплитуды колебаний.

Это означает, что u(t) должно зависеть от ф(Т), т. е. не что иное как формирование воздействия в виде обратной связи.
Задача синтеза обратной связи, обеспечивающей достижение заданного уровня энергии, была решена выше методом скоростного градиента. Для осциллятора (4.26) типовые (линейный и релейный) законы обратной связи, предложенные в [4, 81, 124], имеют вид (3.13), (3.14), т. е. такой же, как и для простого маятника.
Пусть теперь в системе (4.26) имеются потери (диссипация) типа вязкого трения, т. е. вместо (4.26) рассматривается уравнение
(4.29)
ф + дф + П (ф) = и,
где д 0 коэффициент диссипации. Для линейных систем вида (4.29) (при П((/?) = |cJq(/92) резонансом принято называть режим наибольшей амплитуды колебаний, который наступает при воздействии (4.28) с частотой и2 = и0 д2/4. При этом для малых д О колебания в системе (4.28), (4.29) имеют амплитуду
^ = (1 + 0(е2))
дио
и среднюю энергию за период
(4.30)
Колебания нелинейного осциллятора (4.29) при воздействии (3.13) или (3.14) также могут достичь больших значений амплитуды. Из теоремы 4.2 следует, что в системе (3.14), (4.29) достигается значение энергии, не меньшее чем
(4.31)
если параметры закона (3.14) выбраны так, что Я* Я. Поскольку
(4.31) при малых д приближается к (4.30), можно сказать, что обратная связь (3.13) или (3.14) создает в нелинейной системе (4.29) резонансный режим, энергия которого (в частном случае гармонического осциллятора) не меньше, чем энергия колебаний при возбуждении гармоникой с резонансной частотой. Описанное явление будем называть резонанс с обратной связью (feedback resonance, f-resonanee).
Надо сказать, что понимание резонанса в физике осталось практически неизменным со времен Галилея. В подавляющем большинстве работ рассматривается гармоническое (в крайнем случае периодическое) входное воздействие. В книге [12], первое издание которой вышло в 1937 г., было введено понятие авторезонанса как резонанса под действием силы, порождаемой движением самой системы, т. е. указывалось на возможность воздействий в виде обратной связи. Однако в [12] был рассмотрен лишь случай линейной системы второго порядка при наличии реле в обратной связи, для которого были даны оценки размера предельных циклов.

Система при этом рассматривалась как замкнутая, т.е. фактически исследовался внутренний резонанс в системе, что, по-видимому, и мотивировало введение термина авторезонанс. В дальнейшем возбуждение продолжали рассматривать как периодическую функцию, допуская лишь возможность адиабатического (медленного по сравнению с основным тоном колебаний) изменения частоты [1, 41, 184].
Описанное выше явление резонанса с обратной связью, впервые исследованное в работах [82, 126, 127, 128] возникает при подаче внешнего воздействия. Воздействия вида (3.13), (3.14), (4.12), меняют свой характер в темпе процесса, что позволяет уменьшить требуемую мощность управления и существенно ускорить достижение заданного режима.
Интересно, что галилеево описание резонанса не противоречит наличию обратной связи. Более того, оно подсказывает, как ее использовать для введения маятника в резонансный режим: надо просто ...дуть в соответствующий его качанию момент.
Явление резонанса с обратной связью может иметь разнообразные применения. Некоторые из них рассмотрены далее.

Индекс возбудимости маятниковых систем

Введенные выше характеристики (индексы) возбудимости определяют возможную глубину (степень) резонансного режима в системе. Знание индекса возбудимости нелинейной системы позволяет судить также о ее Близости к границе устойчивости и об ее стабилизирующих свойствах.

В частности, индекс возбудимости занимает место амплитудно-частотной характеристики в критериях абсолютной устойчивости для случая, когда номинальная система нелинейна [128, 129].
Индекс возбудимости может быть измерен в ходе вычислительного или натурного эксперимента, как и обычная частотная характеристика линейной системы. Однако, в отличие от измерения частотной характеристики, когда на вход системы подается гармоническое воздействие (4.28) с постоянной амплитудой и меняющейся частотой, при измерении характеристики возбудимости меняется амплитуда (уровень) входного сигнала, а сам сигнал задается в виде обратной связи. Точному расчету величин Е±(у) препятствует необходимость решения сложной задачи оптимального синтеза.

Однако нижнюю оценку можно получить, подавая входной сигнал (4.12) скоростноградиентного типа, являющийся локально-оптимальным. Можно показать, по аналогии с [84], что при малых у подача входного сигнала (4.12) дает приближенное значение для Е(у) с точностью порядка у.
Приведем примеры построения графиков индекса возбудимости (называемых также характеристиками возбудимости) для маятниковых систем.
Характеристика возбудимости простого маятника, построенная по его модели
ф(і) + дф(Т) + J0 sin ДТ) = u(t) (4.32)
по отношению к энергии при локально-оптимальном (скоростно-градиентном) воздействии
и = у sign ф (4.33)
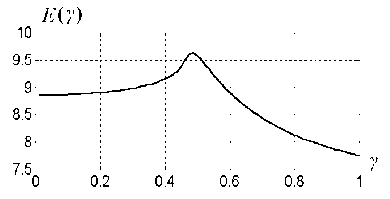
приведена на рис. 4.2.

Значения параметров системы заданы как = Ю.О с-2, д = 0.1 с-1, а начальные условия берутся ср(0) = 0, ф(0) = 10_ю с~К Интересно, что из результатов примера 4.1 следует, что Е(у) у^л/2 9.0 при у 0, что неплохо согласуется с рис.
4.2. На рис.

4.3 представлены результаты измерений характеристики возбудимости на экспериментальной маятниковой установке ИПМаш РАН [75]. Видно, что качественный характер результатов моделирования и эксперимента одинаков.

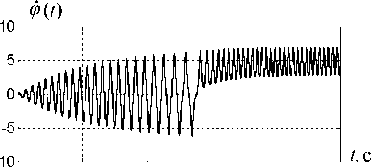
Пик графика Е(у) соответствует уровню входного сигнала, раскачивающего маятник до верхнего положения, т. е. по виду кривой Е(y) возможно определение критических уровней потенциальной энергии системы. Типичный график изменения выхода ф(Т) представлен на рис.

4.4.
Для сложных систем характеристика возбудимости может иметь весьма причудливый вид и содержащуюся в ней информацию о тонких динамических свойствах системы извлечь не просто. В качестве примера рассмотрим систему из двух связанных маятников:
(4.34)
1 + 6Ф1 + ^1 sin ф1 + К(ф1 - 2) = u(t), Ф2 + Q22 + ^2 Sin ф2 + К(ф2 - Ф1) = 0,
где k 0 коэффициент связи. Пусть выходом системы является ее энергия:
н = 2 W + ФІ) + 0 - cos ^і) + ^1(1 cos ip₂) + 2^ + (pi) -
Подадим входное воздействие, аналогичное (4.33):
и = y sign (4.35)
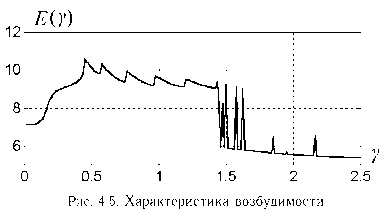
В частном случае k = 0 и ф₂(0) = ^₂(0) = 0 график индекса возбудимости Е(y) совпадает с тем, что получено для одного маятника (рис. 4.2). С ростом коэффициента связи k динамика нелинейной системы (4.34) усложняется, что отражается на виде функции E(y).

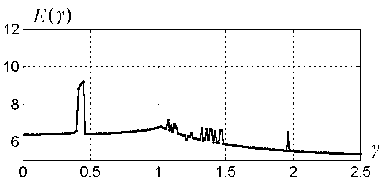
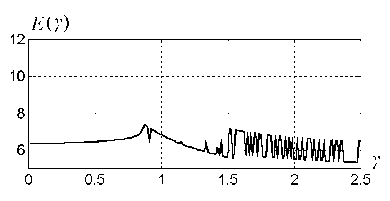
Графики возбудимости для k = 0.25, 0.5, 1.0, 5.0 изображены на рис. 4.5, 4.7, 4.9, 4.11.

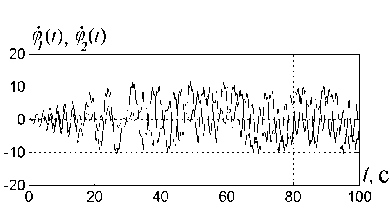
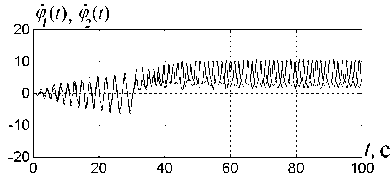
На рис. 4.6, 4.8, 4.10, 4.12 показаны типичные графики процессов ^₁(t), ?₂(Т).

Начальные условия ф₁(0) = ф₂(0) = 0, ^(0) = 10-10 с-1, ?₂(0) = 0 с-1, а значения параметров выбраны д₁ = 0₂ = 0.1 с-1, ^2 = ^2 = 10 с-2. При вычислении Е(y) время моделирования взято равным 500 с. Для усреднения энергии использован метод скользящего среднего по 500 шагам с интервалом считывания 0.05 с.
Из рисунков видно, что с ростом коэффициента связи k характеристика возбудимости Е(y) становится все более и более изрезанной, число ее экстремумов возрастает. Экстремумы E(y) соответствуют бифуркациям (качественным изменениям поведения траекторий системы) изменению числа качаний маятника до перехода во вращательный режим и изменению числа оборотов проскальзывания маятников друг относительно друга. В области многоэкстремальности Е(у) движение маятников носит нерегулярный, хаотический характер.

Характеристики возбудимости относительно других выходов имеют другой вид и позволяют судить о других свойствах системы.
В заключение еще раз отметим, что индекс (характеристика) возбудимости является, подобно амплитудно-частотной характеристике для линейных систем, интегральной количественной оценкой резонансных динамических свойств нелинейной системы. Она находит применение при исследовании сложных колебательных процессов и систем, в частности при исследовании динамики многороторных управляемых вибрационных установок [75].

Рис. 4.2. Характеристика возбудимости маятника (4.32) при q = 0.1 с-1, JQ = 10 -2 (моделирование)

Рис. 4.3.

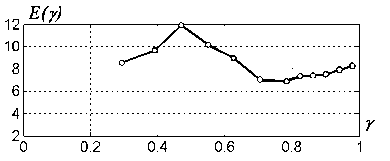
Характеристика возбудимости маятника (эксперимент).

Рис. 4.4. Типичная траектория системы (4.32), (4.33)
при у =1.25.

двухмаятниковой системы (4.34) при К = 0.25

Рис. 4.6.

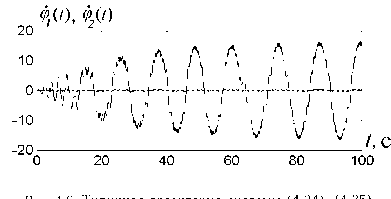
Типичная траектория системы (4.34), (4.35) при К = 0.25, у = 1.25.

Рис. 4.7. Характеристика возбудимости двухмаятниковой системы (4.34)
при К = 0.5.

Рис. 4.8.

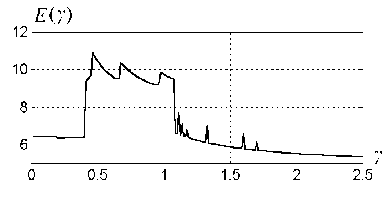
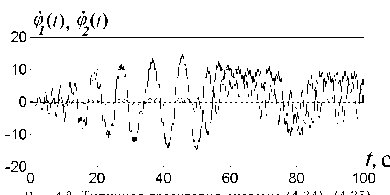
Типичная траектория системы (4.34), (4.35) при k = 0.5, y = 1.25.

Рис. 4.9. Характеристика возбудимости двухмаятниковой системы (4.34)
при k = 1.0.

Рис. 4.10. Типичный процесс в двухмаятниковой системе (4.34), (4.35)
при k = 1.0, y = 1.25.

Рис. 4.11. Характеристика возбудимости двухмаятниковой системы (4.34)
при k = 5.0.

Рис. 4.12. Типичный процесс в двухмаятниковой системе (4.34), (4.35)
при k = 5.0, у = 1.25.

Управление синхронизацией

Явление синхронизации имеет многочисленные применения в механике и физике [14, 15, 70], в вибрационных технологиях [14, 15], в радиотехнике и технике связи [50, 53] и в других областях. В последние годы возрастает интерес к задачам управления синхронизацией, состоящим в обеспечении синхронного протекания процессов в системе путем введения дополнительных обратных связей. Подобные задачи рассматривались ранее для линейных систем [59, 150], а также для релейного закона отключения опережающего роторав многороторном вибровозбудителе [10].

Применение современных методов синтеза законов управления позволяет расширить класс систем, обладающих синхронными режимами, повысить их устойчивость и робастность. С начала 1990-х годов значительно вырос интерес к так называемой хаотической синхронизации, когда каждая из синхронизируемых подсистем продолжает совершать сложные, хаотические колебания и после установления синхронного режима [6, 140, 196]. Предложен целый ряд способов использования эффекта хаотической синхронизации для повышения скрытности и надежности передачи информации (см. например обзоры и специальные выпуски журналов [32, 156, 158]).

Изучаются закономерности и способы обеспечения синхронизации в массивах взаимодействующих осцилляторов, с применениями к синхронизации биологических объектов, искусственных и естественных нейронов и т.д. [70, 96, 208].
В настоящей главе даются общие определения синхронизации, охватывающие как случай самосинхронизации, так и случай управляемой синхронизации. Рассматриваются различные классы задач управления синхронизацией, демонстрирующие общие подходы к анализу и синтезу процессов синхронизации на основе методов пасси-фикации и скоростного градиента.

Определения синхронизации

Как уже было сказано в главе 2, под синхронизацией понимается согласованное во времени функционирование двух или нескольких процессов или объектов. В частности, это может быть совпадение или сближение переменных состояния двух или нескольких систем, или согласованное изменение некоторых количественных характеристик систем.
В определенных случаях синхронизация возникает в силу естественных свойств самой системы взаимодействующих объектов. Примером может служить частотная синхронизация колеблющихся или вращающихся тел (см. ниже).

В таких случаях говорят о самосинхронизации.
В других случаях для согласования поведения объектов необходимо привнесение в систему дополнительных связей или воздействий. Тогда говорят о принудительной или управляемой синхронизации.

В этих случаях под синхронизацией понимают приведение процессов к синхронному протеканию.
В связи с бурным ростом интереса к проблемам синхронизации в различных областях науки и техники возникла парадоксальная ситуация, характерная для многих быстро развивающихся наук: отдельные группы ученых, работающие в определенных направлениях теории синхронизации, плохо знают об исследованиях в других направлениях и, как правило, на них не ссылаются [75]. В результате достижения одних групп исследователей остаются незамеченными представителями других групп и поэтому не используются ими.

Более того, то, что представляется синхронизацией по мнению одних ученых, вовсе не является синхронизацией в глазах других исследователей.
Для рассмотрения различных вопросов синхронизации с единых позиций представляется полезным сформулировать общее определение синхронизации процессов или объектов. Первые варианты общих определений для периодических процессов были предложены в [14] (совпадение или кратность средних частот колебательных или вращательных движений) и в [30] (существование асимптотически устойчивого инвариантного тора размерности п т, где т - степень синхронизации). В [14] было отмечено также, что под синхронизацией может пониматься равенство значений некоторых функционалов от координат систем.

Например, в качестве функционалов могут выступать моменты обращения координат в нуль или достижения ими экстремальных значений. По мере изучения синхронизации хаотических процессов возник целый ряд новых вариантов свойства синхронизации: координатная (идентичная) синхронизация [іі, 141, 196]; обобщенная синхронизация [212]; фазовая синхронизация [211] и
Т. д.
Общее определение свойств синхронизации, охватывающее как случай самосинхронизации, так и случай управляемой синхронизации было предложено в [103] и развито в работах [75, 104, 102]. Близкие, отличающиеся лишь в деталях варианты описаны в работах [108, 111].

В работе [164] исследуется определение, основанное на понятии инвариантного многообразия динамической системы и охватывающее координатную и обобщенную синхронизацию. Ниже, следуя [75, 102], приводятся общие определения синхронизации, позволяющие легко получать как частные случаи многие известные в литературе определения.

Кинематическое определение

Пусть имеется некоторое число k процессов (объектов), состояние каждого из которых в момент времени Т характеризуется некоторым вектором x(i)(t), і = 1,2, ...,k, где t изменяется на промежутке 0 t то. Предположим сначала, что все вектор-функции х(і)(Т) принадлежат одному и тому же функциональному пространству X.
Пусть задана некоторая числовая характеристика данных процессов, определенная зависящими от времени отображениями С_т : X C, где C есть множество возможных значений С_т.

Содержание раздела