Методы построения алгоритмов управления
На самом деле, программное управление может зависеть еще от параметров, а также от начальных условий объекта управления:
u(T) = U (Т, х0). (2.22)
Как уже говорилось, в задачах вибрационной механики подача управления в виде высокочастотной функции времени на нелинейную систему может качественно изменить ее динамику, например превратить неустойчивое положение равновесия в устойчивое и наоборот.
Еще более широкими возможностями обладает управляющее воздействие, использующее при вычислении u(t) результаты измерений состояния объекта или его выходов (наблюдаемых величин). Такое управление записывается в форме обратной связи по состоянию (state feedback):
u(t) = U (x(t)) (2.23) или по выходу (output feedback): u(t) = и (y(t)). (2.24)
В физических задачах встречаются все три типа управления: постоянное, программное и обратная связь. Поскольку реализация управления в виде обратной связи требует возможности измерения необходимых для построения управления величин, которая часто отсутствует, исследование свойств управляемой системы обычно начинают с изучения возможностей низшей формы постоянного управления, затем переходят к исследованию возможностей управления разомкнутого типа (программного), и лишь после этого ставятся и исследуются задачи управления с обратной связью.
Типичная формулировка задачи управления с учетом особенностей физического исследования имеет следующий вид:
найти все возможные виды поведения системы, которые могут бытъ обеспечены при помощи управляющих функций с нормой, не превышающей заданной (достаточно малой) величины и, возможно, при выполнении заданных ограничений;
При ее решении может быть полезным решение вспомогательной задачи, более характерной для теории управления:
найти управляющую функцию (или закон обратной связи) минимальной нормы, обеспечивающую достижение заданного поведения системы (заданной цели управления).
Методы построения алгоритмов управления
Методология кибернетической физики основана на достижениях теории управления. Применяются методы линейного, нелинейного и адаптивного управления, идентификации (реконструкции) параметров, оценивания состояний и параметров и оптимизации систем. Обычно некоторые параметры физической системы неизвестны, а некоторые переменные недоступны для измерения.
По терминологии теории управления это означает, что синтез управления должен выполняться в условиях значительной неопределенности. Поэтому особая роль принадлежит методам робастного и адаптивного управления.
Все перечисленные разделы достаточно хорошо разработаны и составляют основу курсов теории автоматического управления по специальностям, связанным с управлением и автоматизацией. Для ознакомления с ними можно порекомендовать книги [6, 69] Ниже мы кратко опишем два достаточно общих подхода к построению алгоритмов управления в нелинейных и адаптивных системах, систематически применяемые в последующих главах книги: градиентный метод и метод скоростного градиента [61, 79, 80].
Градиентный метод
Как уже было сказано, математическими моделями многих динамических систем в физике, биологии, экономике являются системы разностных уравнений. В случае, если в такой системе может присутствовать управляющее воздействие, ее модель можно записать в виде xk+1 = F (xk, uk) (см. (2.8)), где k = 0,1,2,... номер стадии функционирования дискретной системы или номер очередного момента измерения и подачи управления tk; xk Е вектор переменных состояния (фазовых переменных), uk Е Rm вектор входов (управлений), соответствующих моменту tk. Градиентный метод предназначен для построения управления моделью (2.8) в случае, когда цель управления задана при помощи некоторой гладкой неотрицательной целевой функции Q = Q(x) в виде
Q(хк+і) А, при k k*, (2.25)
где А 0 заданное значение порога точности задачи.
Выразим очередное состояние объекта из (2.8) и подставим в (2.25). Тогда получим приведенную целевую функцию (точнее, семейство функций Qk(и), зависящих от номера шага), непосредственно зависящую от управления:
(2.26)
Qk(u) = Q(Fk(xk, u)).
Градиентный метод основан на изменении вектора uk в направлении, противоположном направлению градиента (вектора из частных производных) от функции Qk по управляющим переменным:
(2.27)
uk+l uk ^k ^ uQk (uk),
где ?ц = , ^}т вектор градиента, 0 коэффициент
шага по управлению. Идея метода хорошо известна в теории оптимизации: при малом Yk поправка Auk = uk+l uk приводит к уменьшению значения функции Qk(u).
В более изощренном выборе нет необходимости, поскольку на следующем шаге управления целевая функция изменится в силу динамики системы. Однако простая форма алгоритма не означает простоты условий его применимости, Условия, гарантирующие достижение цели управления (2.25) в системе (2.8) с алгоритмом (2.27) можно найти в [78, 80]. В их число входят выпуклость функции Qk(u) по и, существование общего решения и = и системы целевых неравенств Qk(u) A и выбор коэффициента шага Yk с зоной нечувствительности: при выполнении текущего целевого неравенства Qk(uk) A выбирается Yk = 0. Подобные условия систематически изучались в рамках метода целевых неравенств, предложенного В.А. Якубовичем в 1966 г., см. [78, 80].
Алгоритмы, подобные (2.27), применяются при управлении дискретными хаотическими системами, а также при управлении хаосом в непрерывных системах на основе линеаризации отображения Пуанкаре.
Отметим, что правая часть алгоритма (2.27) может оказаться зависящей от всего вектора состояния xk, недоступного измерению. Стандартные рецепты для этого случая состоят либо в восстановлении недоступных для измерения координат при помощи специального динамического звена наблюдателя (фильтра), либо в переходе от модели динамики системы в виде уравнения состояния (2.8) к модели в форме вход-выход:
(2.28)
yk+i ф(ук,... ,yk-n, uk,..., uk-n+i).
2.4.2 Метод скоростного градиента
Метод предназначен для решения задач управления непрерывными по времени системами, в которых цель управления задана при помощи целевой функции. Опишем построение алгоритмов скоростного градиента для непрерывной нестационарной системы (2.5) при цели управления, заданной соотношением (2.21), где Q(х, Т) гладкая целевая функция.
Для построения алгоритма вычисляется скалярная функция Q = ^(х, и, Т) скорость изменения величины Qt = Q(x(t), Т) в силу уравнения объекта (2.5):
dQ(x, t) dt
т
+ [VxQ(x, T)] F(x, u, t).
и(х, и, t)
Затем находится градиент функции и(х, и, Т) по входным переменным
ди т ~dF~ ди ди т
VxQ(х, Т).
VиШ(х, и, Т)
Наконец, задается алгоритм изменения и(Т) дифференциальным уравнением
Du
dt
(2.29)
TV и и(х, и, Т),
где Г = Гг 0 симметрическая положительно определенная матрица, например Г = diag {71,..., Ym}, Yi 0. Алгоритм (2.29) естественно назвать алгоритмом скоростного градиента (АСГ), поскольку в нем изменение и(Т) происходит пропорционально градиенту скорости изменения QT.
Происхождение алгоритма (2.29) можно объяснить следующим образом. Для достижения ЦУ (2.21) желательно изменять и(Т) в направлении уменьшения Q(х(Т), Т). Однако Q(х(Т), Т) не зависит от и(Т), найти такое направление затруднительно (в частности, это связано с нахождением функций чувствительности).
Вместо этого можно пытаться уменьшить Q, стремясь к выполнению неравенства Q 0, означающего, в свою очередь уменьшение Q(x(T), Т). Функция Q = и(х, и, Т) уже явно зависит от и, что и позволяет написать алгоритм (2.29).
Можно также рассматривать АСГ как непрерывный аналог или идеализированным вариант дискретного градиентного алгоритма, поскольку при малом шаге дискретизации градиент целевой функции, совпадающий с градиентом ее приращения, приближается по направлению к градиенту скорости изменения целевой функции в силу объекта.
В качестве примера выпишем АСГ для задачи регулирования линейной по входам системы
Х = А(х, t) + B(x, t)u, (2.30)
где A(x, t) п-вектор, B(x, t) n x m-матрица. Уравнение (2.30) можно переписать также в виде
Х= А(х, Т) + ^ Ві(х, t)u, (2.31)
і=і
где иі компоненты вектора и е Rm; Ві(х, Т) е Rn столбцы матрицы В(х, Т).
Пусть целевая функция имеет вид:
1 т
Q(x,t) = -[у -y*(t)] P[y-y*(t)], (2.32)
где у = G(x, Т) е R; у*(Т) е R задающее воздействие (желаемая траектория выхода); G(x, Т) гладкая вектор-функция, Р симметричная положительно-определенная I x I-матрица. Скорость изменения Q(х(Т), Т) будет равна
и(х, и, Т) = [у у*(Т)]тР[СА(х, Т) + СВ(х, t)u у*(Т)], (2.33)
где С = С(х, Т) = dG(x, t)/dx, а скоростной градиент и алгоритм скоростного градиента примут вид, соответственно
?ии(х, и, Т) = В(х, Т)тСР[у у*(Т)], (2.34)
Du т т
= -ГВ(х,і)тСтРІу-уШ (2.35)
В качестве матрицы усиления Г часто берется диагональная (Г = = diag {уі}) или скалярная (Г = уі) матрица (уі, у положительные числа). Алгоритм (2.35) при В(х, Т) = const и С(х, Т) = const представляет собой хорошо известный интегральный закон регулирования.
Аналогичным образом строится и обобщение другого классического закона регулирования пропорционального. Это так называемый алгоритм скоростного градиента в конечной форме:
u(t) = u0 rVuu(x(t), u(t), t), (2.36)
где u0 некоторое начальное (опорное) значение управления (обычно берется uo = 0).
Используются алгоритмы и еще более общей структуры:
и(Т) = и0 уф(х(й), u(t), t), (2.37)
где у 0 скалярный множитель шага (коэффициент усиления), а вектор-функция ^(х, u, Т) удовлетворяет условию псевдоградиент-ности
ф(х, u, t)TVuи(х, u, Т) 0. (2.38)
Алгоритмы вида (2.37) называют алгоритмами скоростного псевдоградиента. Их частным случаем является так называемый знаковый или релейный алгоритм
u(T) = u0 у sign Vuu(x(t), u(t), t), (2.39)
где знак (sign) для вектора понимается покомпонентно: для вектора х = col (хі,..., хт) имеем signх = col (signXi,..., signxm).
Для правильного и обоснованного выбора параметров алгоритмов скоростного градиента требуется проверка условий их применимости. Такие условия для различных случаев можно найти в [61, 78, 80]. Основные из них: выпуклость функции и(х, u, Т) по u и существование идеального управления вектора u* такого, что и(х, u*, Т) 0 для всех х (условие достижимости).
Далее в книге метод скоростного градиента будет использоваться для управления инвариантами гамильтоновых систем. Соответствующие условия применимости будут приведены ниже, в гл. 3.
Метод скоростного градиента и градиентный метод тесно связаны с понятием функции Ляпунова V(х) функции состояния системы, убывающей вдоль ее траекторий. Функция Ляпунова является
абстрактным аналогом таких физических характеристик как энергия и энтропия. Важно, что функция Ляпунова может использоваться не только для анализа, но и для синтеза систем, т.е. для решения обратных задач.
В частности, конечная форма СГ-алгоритмов получается, если в качестве функции Ляпунова взять саму целевую функцию: V(х) = Q(x). Дифференциальная форма СГ-алгоритмов соответствует выбору V(х, и) = Q(х) + 0.5(и и*)тГ_1(и и*), где и* - желае
мое (идеальное) значение управляющих переменных. При обосновании градиентного метода в качестве функции Ляпунова используется квадрат расстояния до идеального управления: V(и) = Іи и*|2.
Результаты: законы кибернетической физики
Значительная часть результатов в традиционных разделах физики представлена или может быть представлена в виде законов сохранения, утверждающих, что некоторые величины не изменяются в процессе эволюции системы. Такая форма представления не вполне соответствует задачам кибернетической физики, результаты в которых должны устанавливать, до какой степени эволюция системы может быть изменена при помощи управления. Поэтому результаты в киберфизике формулируются не как законы сохранения, а как законы преобразования, определяющие класс возможных видов поведения, достижимых при помощи управлений из заданного класса, т. е. определяющие пределы управления.
Приведем несколько примеров.
Первый пример относится к управлению инвариантом (константой движения) консервативной системы, а закон преобразования отвечает на вопрос: что можно сделать с консервативной физической системой введением обратной связи? Результаты работ [220, 221] (см. далее п. 3.1) можно интерпретировать так:
Значение любого управляемого инварианта свободной системы можно изменить на произвольную величину при помощи сколь угодно малой обратной связи.
Следующий закон преобразования относится к диссипативным системам (см. далее п. 3.2). Он показывает, что эффективность малой обратной связи тем выше, чем ближе система к консервативной и дает количественную оценку явления резонанса с обратной связью в нелинейных осцилляторах.
Для управляемой лагранжевой или гамильтоновой системы с малой диссипацией степени р уровень энергии, достижимой при помощи управления уровня у имеет порядок (7/р)2.
Ряд законов преобразования установлен в работах по управлению хаосом [27, 140, 166, 192, 199, 219]. В частности, принцип, предложенный в основополагающей работе [192] (закон Отта-Гре-боджи-Йорке), можно кратко сформулировать следующим образом:
Каждая управляемая хаотическая траектория может быть преобразована в периодическую при помощи сколь угодно малого управления.
Отметим, что требование хаотичности траектории можно существенно ослабить, заменив рекуррентностью, а иногда еще более слабым требованием типа консервативности (выборочная консервативность), если рассматривать систему только в моменты прохождения траектории через секущую поверхность.
Перечисленные и другие результаты подобного типа дают возможность изучать различные свойства физических систем при воздействии обратных связей. Примеры можно найти в последующих главах книги и в упомянутых там ссылках на литературу. Присутствующий в приведенных выше формулировках термин управляе-маяозначает принципиальную разрешимость задачи. Достаточные условия для управляемости составляют предмет математических исследований законов преобразования.
Ряд формулировок можно найти в теоремах последующих глав книги.
Подводя итог, еще раз повторим, что предметом кибернетической физики является исследование свойств физических систем при наличии обратных связей с окружающей средой. В первую очередь представляет интерес случай слабых обратных связей, не вносящих существенных нарушений в естественное функционирование системы.
Методология кибернетической физики основана на методах построения математических моделей управляемых систем, методах оценивания переменных и параметров систем и методах синтеза обратных связей, развитых в кибернетике. Отличие моделей управляемых систем (кибернетических моделей) от традиционных для физики и механики моделей динамики состоит в том, что в них явно указываются входы и выходы системы, поскольку это существенно при построении обратных связей.
В отличие от законов сохранения традиционных областей результаты кибернетической физики формулируются как законы преобразования, устанавливающие возможности и границы изменения свойств системы при помощи управления.
Таким образом, в фундаменте методологии лежит математическое моделирование: построение, исследование и использование математических моделей [7]. При исследовании моделей широко применяется вычислительный эксперимент: то, что не удается доказать математическими средствами, часто оказывается возможным проверить путем компьютерного моделирования. Особенностью очерченного выше направления является еще и то, что в нем осуществляется синтез описательной и предписательной наук.
Подобное расширение сферы и методологии физических исследований способствует достижению их основной цели: лучшему пониманию природы. Развитие нового направления является плодотворным и для кибернетики, обогащающейся новыми задачами и приложениями.
Управление консервативными системами
В настоящей главе рассматриваются задачи управления, в которых в качестве целевых функций выступают функции от основных характеристик физических систем, таких как полная энергия и другие инварианты свободного движения. Для описания динамики управляемых систем используется гамильтонов и лагранжев формализм.
Устанавливаются условия достижимости и предлагаются алгоритмы достижения заданных значений инвариантов путем управления с обратной связью на основе скоростного градиента. Показывается, что достижение целей управления возможно при сколь угодно малой интенсивности (мощности) управления.
Управление энергией гамильтоновых систем
Постановка задачи
Одной из важнейших физических величин является энергия. Энергия представляет собой не только основной инвариант физической системы и ключ к ее описанию на основе гамильтонова формализма, но и меру взаимодействия различных систем. По своему физическому смыслу внутренняя энергия системы является мерой ее возможности совершения работы.
Задача изменения энергии за счет внешних воздействий (управлений) может иметь как теоретическое, так и практическое значение. Например, для энергосберегающих технологий важной задачей является преобразование энергии системы без неоправданных потерь энергии внешних воздействий.
Исключительное значение энергии как функции состояния физической системы состоит в том, что функционал полной энергии гамильтониан может являться основой для построения математического описания динамики системы. Уравнения динамики в гамильтоновой форме используются для описания самых разнообразных физических систем и явлений: от движения космических тел до движения молекулярных ансамблей.
Это еще более усиливает интерес к задачам управления энергией систем. Поэтому изучение фундаментальных законов преобразования свойств систем при помощи управления естественно начать с законов преобразования энергии.
В этой главе будем предполагать, что система консервативна, т.е. что потерями и диссипацией можно пренебречь. Тогда в свободном движении (т.е. при отсутствии внешних сил) энергия является инвариантом системы.
Поэтому оправданной является постановка задачи о переводе системы с одного уровня энергии на другой при помощи малого (в идеале сколь угодно малого) по величине управления.
Итак, рассмотрим задачу управления, в которой целью управления является достижение и поддержание заданного уровня энергии системы. Пусть математическая модель системы задана в гамильтоновой форме:
dH(g,p,u)
дді
дН(д,р, и) dpi
(3.1)
i = 1, . ..,П,
ді =
рі =
где n - число степеней свободы; д = col(gb ... ,дп), р = со1(рь ...,рп) - векторы обобщенных координат и обобщенных импульсов, образующие вектор состояния системы х = col(g, р); Н = Н(д, р, и) - гамильтониан управляемой системы; и(Т) е Rm - вход (вектор внешних обобщенных сил). Предполагается, что гамильтониан Н(д, р, и) = Н(х, и) непрерывно дифференцируемая функция своих аргументов. Модель (3.1) может быть переписана в следующей форме:
(3.2)
g = VpH(g, р, и), р = -VgH(g, р, и).
Рассмотрим задачу приближения к заданному уровню Н* энергии свободной (неуправляемой) системы, т.е. зададим цель управления в виде
lim Но(д(Т),р(Т)) = Н*, (3.3)
где Н0(д,р) = Н(д,р,0) гамильтониан свободной системы, описываемой уравнениями
(3.4)
g = ?рНо(д, р), р = -?дНо(д, р).
Введем целевую функцию
Q(x)=X-(H0(q,p)-H,f, (3.5)
где х = co1(q, р). Тогда цель управления (3.3) примет вид
lim Q(х(Т)) = 0. (3.6)
too
В дальнейшем будем предполагать, что гамильтониан линеен по управлению:
Н(q,р, и) = Ho(q,Р) + Hi(q,р)ти,
где H0(q, р) гамильтониан свободной системы; Hi(q, р) m-мерный вектор так называемых гамильтонианов взаимодействия.
Пример 3.1. Для модели простого маятника гамильтониан свободной системы имеет вид
2/Ho(Q, Р)
+ mgl(1
cos q),
(3.7)
где q(T) g R1 угловая координата; p импульс системы; J момент инерции относительно оси вращения, т масса, I расстояние между осью вращения и центром тяжести маятника; g ускорение свободного падения. Если в качестве управляющего воздействия выбран вращающий момент, приложенный к оси подвеса, то уравнения движения в гамильтоновой форме записываются следующим образом:
(3.8)
q = J 1 р,
р = sin Q + u(T),
где u(T) управляющий момент. Из (3.8) следует, что р = Jq, а гамильтониан взаимодействия имеет вид H1(q, р) = Q. Цель (3.3) будет соответствовать стабилизации маятника в нижнем положении при Н = 0, раскачке маятника до амплитуды
Л 7Д
q* = arccos 1---
mgl
при 0 Н 2mgl или приведению маятника во вращение при Н 2mgl. Значение Н = 2mgl исключительное. Оно соответствует движению по сепаратрисе множеству, состоящему из счетного числа гладких кривых, разделяющих на фазовой плоскости области колебательного и вращательного движения. ?
Алгоритм управления
Применим для решения задачи метод скоростного градиента (см. п.2.4.2).
Прежде всего напомним, что скобкой Пуассона гладких функций f (q, р) и g(q, р) называется функция
Для применения метода скоростного градиента вычислим скорость изменения целевой функции в силу управляемой системы
а затем скоростной градиент по и: VUQ = (Н Н){Н0, Н1}т.
Теперь легко выписать алгоритмы скоростного градиента в конечной форме, например в линейном и релейном вариантах:
и = 7(Но Н ){Но, НДТ, и = Ysign ((Но Н„){Но, Н}т),
(3.10)
(3.11)
где y 0 коэффициент усиления. Можно применять и другие варианты общего алгоритма, выбирая в соотношении
(3.12)
ф ((Но Н){Но, Hi }т)
в качестве ф некоторую вектор-функцию со значениями в Rm, удовлетворяющую условию ф(г)тz 0 при z е Rm, z = О (условие строгой псевдоградиентности).
Замечание 3.1. Если функция ф^) разрывна (в частности, для релейного алгоритма (3.11), то правые части уравнений замкнутой системы управления также разрывны и анализ поведения решений такой системы требует осторожности, в силу возможной неединственности решений, скользящих режимов и т.п. Даже само понятие решения системы с разрывными правыми частями требует специального определения.
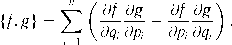
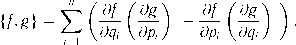
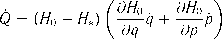
В то же время для рассматриваемых в этой книге систем при использовании для их исследования метод функций Ляпунова сложностей не возникает, а для формального определения решения можно брать любое из известных (см. [6]). Тем не менее, строгие формулировки далее будут даваться только для систем с непрерывными правыми частями. ?
Пример 3.1 (продолжение). Алгоритмы скоростного градиента (3.10), (3.11) в случае маятника (3.8) принимают простой вид:
и = -y(Ho - Н,)и, и = -ysign ((Но - Н,)U).
Условия достижения цели управления
Возможности изменения свойств управляемой гамильтоновой системы путем воздействия на нее управления определяются свойствами построенной замкнутой системы. Прежде всего установим математические условия достижения цели (3.3).
Теорема 3.1 [61, 125, 140]. Пустъ первые и вторые частные производные функций Но,Н1 на множестве По = {х : Q(x) Qo} ограничены для некоторого Q00, а функция ф^) в (3.12) непрерывна и удовлетворяет условию строгой псевдоградиентности ф(z)1z 0 при z е Rm, z = 0.
Тогда алгоритм (3.12) в системе (3.2) при начальном условии х(0) е П0 обеспечивает соотношение u(t) ^ 0 при t и, кроме того, альтернативу: на траектории x(t) либо достигается цель (3.3), либо обеспечивается сходимость {Н0, H1}(x(t)) 0 при t.
Пустъ дополнительно выполнены следующие условия.
At, Для любого с = И* существует е 0 такое, что любое непустое связное подмножество множества
Dec = {х : \{Ио(х), Иі(х)}\ е, Ио(х) с\ е}П По ограничено.
