Метод линеаризации отображения Пуанкаре

В механике возможность значительного изменения динамики системы при помощи периодического сигнала возбуждения известна давно (см. [38, 226] а также ссылки в [14, 15, 95]). В известных работах, однако, рассматривалась только задача стабилизации системы либо в заданном состоянии равновесия, либо относительно заданной (целевой, опорной) траектории.
Обширная физическая литература посвящена исследованию влияния среднечастотных возбуждений, т. е. таких, частота которых близка к частоте собственных колебаний системы. Еще в середине 1980-х годов была обнаружена возможность подавления хаоса путем подачи гармонического воздействия для системы Лоренца [33] и для системы четвертого порядка, служащей моделью динамики двух взаимодействующих популяций [2, 3].
Перечисленные результаты основаны на компьютерном моделировании. Первые попытки теоретического осмысления данного явления даны в работах [177, 200], в которых метод Мельникова применен к исследованию так называемого осциллятора Дуффинга-Холмса
ф сф + Ъф = аф + D cos(uT). (6.4)
С этой целью правая часть (6.4) рассматривалась как малое возмущение, действующее на невозмущенную гамильтонову систему. Аналитически вычислялась функция Мельникова, которая отражает скорость изменения расстояния между устойчивым и неустойчивым многообразиями при малых возмущениях. На ее основе получены значения параметров, при которых поведение системы становится хаотическим. Далее вводилось дополнительное возмущение, состоящее в изменении параметра нелинейности Ъ, вместо которого взята функция Ъ(1 + п cos Ш) и находилась новая функция Мельникова.

Численные исследования этой функции показали, что хаотическое поведение можно подавить, если частоту О выбрать близкой к частоте исходного возбуждения и. Этот эффект был подтвержден экспериментально с помощью установки, содержащей два постоянных магнита, электромагнитный вибратор и оптический датчик. Аналогичные и более точные результаты для осцилляторов с одной степенью свободы общего вида получены в [114, 115].

Развитие и аналитическое обоснование результатов [2, 3], а также обзор исследований по проблеме можно найти в [54].
Выбор функции возбуждения может быть связан с видом присущей системе нелинейности. Рассмотрим этот метод подробнее. Пусть модель объекта управления имеет вид:
Х = f (x) + Bu, x e Rn, u e Rm. (6.5)
Положим, что m = n и det В = 0. Если x*(t) - желаемая траектория управляемого движения, то представляется разумным выбирать функцию возбуждения в виде: [154]
и*(Т) = В-1 (ё*(Т) - f (х*(Т))) , (6.6)
(так называемое воздействие Хюблера) поскольку при таком выборе функция х* (Т) удовлетворяет уравнениям движения возбужденной системы. Уравнение ошибки е = х х*(Т) в этом случае имеет вид ё = f(e + х*(Т)) f(x*(t)). Поэтому, если линеаризованная система с матрицей А(Т) = df (х*(Т))/дх равномерно устойчива в том смысле, что для некоторого Л 0 и для всех t 0 выполнено А(Т) + A(t)1 ЛІ_п, то все решения (6.5), (6.6) сходятся к х*(Т).

Более общие условия сходимости приведены в монографии [140]. Если т п и матрица В - вырожденная, то аналогичный результат можно получить при выполнении следующего условия согласованности: значения вектор-функции ё*(Т) f(х*(Т)) должны лежать в линейном подпространстве, порожденном столбцами матрицы В. Тогда соответствующее управление можно взять в виде и*(Т) = В+(Х*(Т) f (х*(Т)), где В+ есть псевдообратная к В матрица. Несмотря на то что выполнение условия равномерной устойчивости исключает возникновение хаотических (т. е. неустойчивых) траекторий, как отмечено в ряде статей, если области с неустойчивым поведением не являются доминирующими, то наблюдается некоторая локальная сходимость к хаотическим траекториям.

Повысить степень устойчивости можно, вводя в (6.6) обратную связь по ошибке слежения (см. ниже п.6.5).
Обобщая, можно сказать, что к настоящему времени разработано множество методов хаотическими процессами в разомкнутом контуре (управления программным воздействием). Большинство из этих методов исследовано численно в частных случаях и для модельных задач.

Однако общая задача возбуждения или подавления хаотических колебаний с помощью программного сигнала управления по-прежнему остается открытой.

Метод линеаризации отображения Пуанкаре (OGY-метод)

Как уже не раз отмечалось, взрыв интереса к управлению хаотическими процессами был вызван публикацией Е. Отта, С. Гребоджи и Дж. Йорке [192].

В их работе высказаны две ключевые идеи: использование при синтезе регулятора дискретной модели системы, основанной на линеаризации отображения Пуанкаре; использование свойства рекуррентности хаотических траекторий и применение управляющего воздействия только в моменты времени, когда траектория возвращается в некоторую окрестность требуемого состояния или заданной орбиты.

В основополагающей статье [192] метод, который теперь принято называть OGY-методом был описан для систем дискретного времени третьего порядка, а его реализация опиралась на текущее (в темпе с управляемым процессом) вычисление собственных векторов и собственных значений матрицы Якоби для отображения Пуанкаре. Позже были предложены многочисленные расширения и трактовки метода, который в современном изложении (см. напр., [107]) выглядит следующим образом.
Пусть управляемый процесс описывается уравнениями состояния
х = F(х, и), (6.7)
где х е , и е R1. Под переменной и здесь, как правило, понимается изменяемый параметр системы, а не стандартная входная управляющая переменная, но для нелинейных систем эта разница не существенна с точки зрения задачи управления.

Пусть требуемая (целевая) траектория х*(Т) является одним из решений (6.7) при u(t) = 0. Эта траектория может быть как периодической, так и хаотической, но в обоих случаях она рекуррентна. Построим поверхность ( сечение Пуанкаре)
S = {х : s(x) = 0}, (6.8)
проходящую через заданную точку х₀ = х*(0) трансверсально к траектории х*(Т) и рассмотрим отображение х ^ Р(х, и), в котором Р(х, и) есть точка первого возвращения на поверхность S решения (6.7), начинающегося в точке х и полученного при постоянном входе и. Отображение х ^ Р(х, и) называется управляемым отобра-жепием Пуанкаре. Вследствие свойства рекуррентности х* (t) это отображение является вполне определенным, по крайней мере, для некоторой окрестности точки х₀. (Строгое определение управляемого отображения Пуанкаре содержит ряд технических деталей [140]). Рассматривая последовательность таких отображений, получаем дискретную систему
хк+і = Р(x_k, щ), (6.9)
где x_k = x(t_k), t_k - момент времени k-ro пересечения поверхности S, a u_k - значение управления u(t) на промежутке между t_k и t_k+₁.
Следующий шаг синтеза закона управления состоит в замене исходной системы (6.7) линеаризованной дискретной системой
(6.10)
Xk+і = Ахк + Вик,
в которой X_k = x_k х₀. Для полученной системы находится стабилизирующее управление, например в виде линейной обратной связи по состоянию u_k = Сх_к. Окончательно предлагаемый закон управления имеет вид
Схк, если \\хк\\А, 0, иначе,
(6.11)
uk
в котором А 0 параметр алгоритма. Ключевой особенностью данного метода является приложение воздействия только в некоторой окрестности целевой траектории путем введения внешней зоны нечувствительности.

Этим достигается малость управляющего воздействия, которое, согласно (6.11), по норме не превышает \\Сx_k||.
Результаты численных исследований подтверждают эффективность подхода. Часто, однако, отмечается низкая скорость сходимости процесса, что является платой за обеспечение глобальной стабилизации траекторий нелинейной системы с помощью малого управления.
Для того чтобы использовать OGY-метод, следует преодолеть два серьезных препятствия: неточность модели системы и неполноту измерений текущего состояния процесса. Второе из них можно устранить, если вместо используемого в исходном алгоритме вектора состояния х перейти к вектору запаздывающих координат, который вводится как X(t) = \y(t), y(t r),...,y(t (N 1)т)]т e Rn, где у = h(x) - измеряемый выход (например, одна из координат системы), а т 0 - время запаздывания. Тогда закон управления принимает вид
I и(ук, Ук,і,..., Ук,ы-і), если \y_k4 - у*\ А, і = 1,... ,N - 1,
Щ = \
10, иначе,
(6.12)
где ук,і = y(tk - іт).
Э. Хант [155] предложил использовать специальный класс алгоритмов (6.12), названный эпизодической пропорциональной обратной связью (occasional proportional feedback, OPF-алгоритм). OPF-алгоритм используется для стабилизации амплитуды предельного цикла. Он основан на измерении локального максимума (или минимума) выхода у(Т), т. е. для него сечение Пуанкаре определяется согласно (6.8), где s(x) = dh/dxF(х,0), что соответствует у = 0. Если обозначить через y_k значение k-го локального максимума, то OPF-алгоритм примет вид

Кук, если У \ А, 0, иначе,
(6.13)
где y_k = y_k у* и у* = h(x₀) - требуемая амплитуда (заданный
уровень) колебаний.
Заметим, что пока не получено полного обоснования алгоритмов (6.12) и (6.13). Основная трудность состоит в оценке точности линеаризованного отображения Пуанкаре в запаздывающих координатах:
yk + а1 yk,1 + - - - + aN-1 yk,N -1 = b1 uk + - - - + bN -1 Uk-N-1. (644)
Чтобы преодолеть первую из отмеченных выше проблем, связанную с неопределенностью линеаризованной модели объекта, в работе [192] и последующих публикациях предложено проводить оценку параметров модели в уравнениях состояния (6.10). Однако в работе [192] не был описан метод, позволяющий извлечь параметры модели (6.10) из результатов измерений выходного процесса.

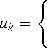
Эта проблема хорошо известна в теории идентификации, и она не простая, поскольку при идентификации в замкнутом контуре хорошее управление может привести к плохому оцениванию.
В работах [6, 27, 131, 132, 140] алгоритм OGY-метода модифицирован и обоснован для класса задач, когда y_k,_i = y_k-i, і = 1,..., N. При этом измерение выходов и изменение управления происходит только в моменты пересечения с поверхностью сечения, y*_t = у* = Н(х₀). При синтезе регулятора использована модель вход-выход (6.14) , имеющая меньше коэффициентов , чем модель (6.10). Для оценки параметров применен метод рекуррентных целевых неравенств В.А. Якубовича, позволяющий разрешить проблему идентификации в замкнутом контуре.

Именно, предложено в закон управления ввести внутреннюю зону нечувствительности (inner deadzone). Алгоритм управления описывается условиями (6.12) и следующими соотношениями:
1, если|ук+1 - у* | Ay и Pk+1 = ^ ^1
1
Sr*
^1
A
1 i = 0, ...,N - 1, 0, иначе; 1 4 - ¦у sign Ьо(ук+1 - У* )wk/IKII2 ?'ш = если рк+1 = 1, иначе; uk+1 = fk+1 wk+1 (if fk+1 если VI
+ fk+1 = fk+1 -(и'_ш-й)/\Ы\\
- K+1 +й)/ІНІ|2 если 4+1 fk+1 если IS
1
V
+ A, если Pk+1 = 0. и и yk+x = 1
и ^К+1 = 1 и Pk+1 = 1
_ (6.15)
где у 0 - коэффициент усиления адаптации, и - максимальное абсолютное значение управления; А связано с размером трубки в пространстве состояния около базовой траектории x(t), где определена модель вход-выход (6.14).
Сочетание этой внутренней зоны нечувствительности с внешней, которая свойственна OGY-методу, приводит к робастности управления, основанного на идентификации по отношению как к неточности модели, так и к ошибкам измерения.

Метод обратной связи с запаздыванием (метод Пирагаса)

В последние годы возрос интерес к методу обратной связи с запаздыванием (time-delayed feedback), предложенному литовским физиком К.Пирагасом [206]. Им рассматривалась задача стабилизации т-периодической орбиты нелинейной системы (2.1) с помощью простого закона обратной связи:
u(t) = K(x(t) x(t т)), (6.16)
где К - коэффициент передачи, т - время запаздывания. Если т равно периоду существующего периодического решения Х(Т) уравнения (2.1) при и = 0 и решение х(Т) уравнения замкнутой системы (2.1),
(6.16) начинается в точке Г = {Х(Т)}, то оно остается в Г для всех t 0. Удивительным, однако, является то, что х(Т) может сходиться к Г, даже если x(0)eГ.
Закон обратной связи (6.16) используется также для стабилизации периодического возбужденного процесса в системе (2.1) с Т-периодической правой частью. Тогда т следует брать равным Т. Естественным образом метод распространяется на задачи стабилизации состояний равновесия и периодических траекторий дискретных систем.
Позже был предложен расширенный метод Пирагаса, при котором управление имеет вид
м
u(T) = K^2rk(y(t Кт) y(t (k + 1)т)), (6.17)
k=0
где у(t) = h(x(t)) e R1 - измеряемый выход; r_k, k = 1, . . . , M -настраиваемые параметры. При r_k = rk, \r\ 1 и M ^ o алгоритм
(6.17) принимает вид
u(t) = K(y(t) y(t т)) + Kru(t т). (6.18)
Несмотря на простой вид алгоритмов (6.16) - (6.18), аналитическое исследование замкнутой системы оказалось сложной задачей.
В работах М.Вассо, Р.Женезио и А. Тези [93, 94] исследована устойчивость возбужденного Т-периодического решения системы Лурье с обобщенным регулятором Пирагаса
u(t) = G(p)(y(t) - y(t - т)), (6.19)
где G(p) (р = d/dt) - передаточная функция фильтра. С использованием методов теории абсолютной устойчивости (см., напр., [50]) в этих работах получены достаточные условия, которым должна удовлетворять передаточная функция линейной части управляемой системы, а также условия на крутизну нелинейной характеристики, которые должны быть выполнены, чтобы фильтр G(p) был стабилизирующим.

В работе [94] предложена процедура синтеза оптимального регулятора, максимизирующего размер области устойчивости.
В работе [229] получено простое необходимое условие стабилизируемое™ с помощью алгоритма Пирагаса (6.16) для одного класса дискретных систем (ограничение нечетности). Условие распространено на более общий случай, а также на системы непрерывного времени независимо в работах [163, 183] на основе теории Флоке. Пусть Ф(Т) - фундаментальная матрица линеаризованной системы относительно заданного т-периодического решения (матрица моно-дромии). Как известно, собственные числа матрицы Ф(т) (мультипликаторы) р_і, і = 1, 2, . . . , п связаны с показателями Ляпунова т-периодического решения р_і соотношениями р_і = т_1 In\Х_І|.

Указанное необходимое условие заключается в том, что число вещественных собственных чисел матрицы Ф(т), больших единицы, не должно быть нечетным. Позже некоторые авторы получали и уточняли приближенные оценки границ значений коэффициента обратной связи К, обеспечивающих стабилизацию периодического решения (см. ссылки в [8]).

Интересно, что полученная в [163] область значений К, обеспечивающих стабилизацию, включает сколь угодно малые значения К при малой степени неустойчивости max р_і, и становится пустой (исчезает) при достаточно большом max р_і.
Если в соотношении (6.18) выбрать \г\ 1, то получаемый алгоритм также можно применять, хотя получаемый регулятор становится неустойчивым. В работе [207] показано, что использование неустойчивого регулятора позволяет существенно ослабить ограничения на матрицу объекта Ф(Т) и, в частности, снять ограничение нечетности.
Несмотря на существенную информацию о свойствах метода Пи-рагаса, полученную в последние годы, проблема нахождения достаточных условий, гарантирующих применимость исходного алгоритма (б.іб), до сих пор остается нерешенной.
Недостатком закона управления (б.іб) является его чувствительность к выбору параметров, особенно - к выбору времени запаздывания т. Очевидно, если система Т-периодическая и цель управления состоит в стабилизации вынужденного Т-периодического решения, то обязательно следует выбирать т = Т. Альтернативным эвристическим приемом является моделирование собственных процессов в системе при начальных условиях х (О) до тех пор, пока текущее состояние х(Т) не приблизится к x(s) при некотором 5 Т, т. е. пока не выполнится условие \x(t) x(s)| е. Тогда выбор т = t s даст разумную оценку периода, а вектор х(Т) будет тем исходным состоянием, при котором начинается управление процессом. Этот подход, однако, часто приводит к завышенным значениям периода. Так как хаотические аттракторы имеют периодические решения с разными периодами, то важно найти и стабилизировать (с помощью малого управления) движение с наименьшим периодом.

Эта проблема пока также остается открытой.

Методы линейного и нелинейного управления

Многие статьи посвящены применению к задачам управления хаосом традиционных подходов и методов автоматического управления. Иногда желаемой цели можно достичь даже с помощью простого пропорционального закона управления.

Например, как показано на ряде примеров в работе [161], метод комбинированного управления (open-plus-closed-loop, OPCL) применим к системам вида Х(Т) = f (х(Т)) + Ви при m = n, det В = 0, т. е. когда число управлений равно числу состояний системы. Предлагаемый закон управления имеет вид
и(Т) = В-1 (х*(Т) f (х*(Т)) К(х х*(Т))) , (6.20)
где К - квадратная матрица коэффициентов усиления и в ряде случаев обеспечивает стабилизацию движения относительно желаемой
траектории х*(Т). С точки зрения теории управления случай т = п, detВ = 0 тривиален.

Действительно, для сходимости решений системы (6.5), (6.20) к желаемой траектории х*(Т) достаточно, чтобы К было выбрано в виде К = кІ_п, где к sup ||А(Т)||, А(Т) = df (х*(Т))/дх.
t
Такой выбор всегда возможен, если вектор-функция х*(Т) ограничена, в частности, для периодических и хаотических траекторий х*(Т).
Для решения более сложных задач при неполном управлении и измерении в теории нелинейного управления разработан целый ряд методов. Один из наиболее развитых - линеаризация обратной связью (feedback linearization) (подробнее см., напр., [61]).

К хаотическим системам он применялся в работах [87, 90] и др. Поясним идею метода для систем, аффинных по управлению
х = f (х)+?(х)и, х е Rn, и е Rm. (6.21)
Система (6.21) называется линеаризуемой обратной связью в области О с Rn, если существуют гладкое обратимое преобразование координат 2 = Ф(х), х е О, и гладкое преобразование обратной связи
и = а(х) + в(х)?, х е О, (6.22)
где ? е Rm - новое управление, такое, что преобразованная система линейна, т. е. ее уравнение в новых координатах имеет вид
2 = Az + В? (6.23)
для некоторых постоянных матриц А, В.
Критерий линеаризуемости обратной связью имеет простой вид для систем с одним входом (м = 1). Именно, система (6.21) линеаризуема обратной связью в окрестности некоторой точки х₀ е Rn тогда и только тогда, когда существует гладкая скалярная функция Н(х) такая, что система имеет в точке х₀ относительную степень п по отношению к выходу у = Н(х).

Напомним, что относительная степень нелинейной системы в точке по определению равна г, если последовательное дифференцирование выходной функции у = Н(х) в силу системы (6.21) дает выражение, содержащее вход точно на г-м шаге. Более формально:
L_gLk_f Н.(х0) = 0, k = 0,1,..., г - 2, L_gLr_t-1 й(х,) = 0, (6.24)
п дф
где через LфФ(x) обозначается производная Ли вектор-функции Ф(х)
вдоль векторного поля Ф: ЛфФ(х) = ?-Ф_г(х).
і=і дх1
Если критерий линеаризуемости выполняется, то система может быть приведена к так называемой канонической форме Бруновскоео (цепи интеграторов) в результате следующих преобразований:
г = ф(х) = col (h(x), Lfh(x),. ..,Ln 1 h(x)),
(6.25)
1
L_gLn~lh(x)
Ln_fh(x) + ^.
Пример 6.1. Рассмотрим систему Лоренца со скалярным управлением в третьем уравнении:
ІХі = а(х2 - Хі),
Х2 = ГХі - Х2 - Х1Х3, (6.26)
Хз = -вхз + Хі Х2 + и.
Выберем у = х_і. Тогда Lfy = у = Х_і = а(х₂ х_і), L2_fу = Lf(Lfy) = Х_і = а (Х₂ Х_і) = а ((г + і) х_і 2х₂ + х_іх₃). Очевидно, относительная степень г = 3 всюду, кроме плоскости х_і = 0. Замену координат можно задать соотношениями хі = гі,і
*2 = -Z₂ + 2ь а
Х₃ = (-2з - (Г - \)Z\ - -2₂ г_і \ а а
т. е. система линеаризуема обратной связью при х_і = 0. Таким образом, система (6.26) эквивалентна линейной в каждом из полупространств {х_і 0}, {х_і 0}. Поскольку линейная система в форме Бруновского вполне управляема, с помощью методов теории линейных систем можно обеспечить любую заданную динамику замкнутой системы.

К недостаткам полученного решения относится то, что оно не является глобальным. Другой существенный недостаток в том, что подобный подход полностью игнорирует собственную динамику системы. Произвольная желаемая динамика достигается ценой Большой мощности управления, требуемой при значительных начальных условиях и при слежении за быстро меняющимся программным движением.

К сожалению, неприменимость к задачам со слабым (маломощным) управлением является типичным недостатком многих работ, использующих традиционые методы нелинейного и адаптивного управления.
В работах [55, 237] исследованы пропорциональные законы управления в расширенном пространстве (х, и) (т. е. динамические обратные связи) в задаче достижения заданной динамики замкнутой системы. Метод [55] распространен на системы с запаздыванием и распределенные системы [56].
Возможности динамических обратных связей могут быть полнее реализованы путем применения наблюдающих устройств (наблюдателей), см. п.5.2. Такой подход дает методическую основу для управления по неполным измерениям. Обзор методов построения нелинейных наблюдателей применительно к задачам управления хаосом дан в [185].

В работе [176] приводятся условия применимости линейных наблюдателей с большим коэффициентом усиления для управления системами с нелинейностями, удовлетворяющими глобальному условию Липшица.
Заметим, что для хаотических моделей глобальное условие Липшица зачастую не выполнено из-за наличия полиномиальных членов, таких как х₁ х₂, х2 и т. д. Это приводит к тому, что ограниченность траекторий хаотических систем, имеющая место в собственном движении, под воздействием управления может нарушаться. Поэтому при выборе управления особое внимание должно быть уделено обеспечению ограниченности решений.

В противном случае решение может уйти на бесконечность за конечное время сорваться, что делает бессмысленным обсуждение вопросов устойчивости и сходимости.
Ряд методов основывается на изменении текущего значения некоторой целевой функции Q(х(Т), Т). Значение Q(x(t), Т) может соответствовать расстоянию между состоянием системы в данный момент времени х(Т) и текущей точкой х*(Т) на заданной траектории, например, Q(х, Т) = \х х*(Т)|2. В качестве целевой функции может быть также выбрана какая-либо мера отклонения текущего положения системы x(t) от заданной целевой поверхности h(x) = О, например, Q(х) = |h(x)|2.

Для систем непрерывного времени значение Q(x) не зависит непосредственно (в тот же момент времени) от сигнала управления и, поэтому вместо Q(х) можно использовать новую непосредственно возникающую целевую функцию Q(x) = dQ/dxF(х, и), т. е. вместо уменьшения значений исходной целевой функции, уменьшать скорость изменения этой функции по времени. Эта идея приводит к методу скоростного градиента (см. п.2.4.2), использование которого для управления хаотическими системами было предложено в [124, 139].
При решении задач стабилизации относительного заданного состояния, или целевого многообразия, использовались различные методы теории нелинейного управления: линеаризация обратной связью (feedback linearization ); теория центрального многообразия (centre manifold); процедуры бэкстеппинга (backstepping) и итеративный синтез (iterative design); метод пассификации метод систем с переменной структурой (СПС); теория абсолютной устойчивости; Н_ж-оптимальный синтез и т.д., см. ссылки в [8]. Заметим, что СПС-алгоритмы с поверхностью переключения h(x) = 0 совпадают с алгоритмами скоростного градиента, для которых целевая функция взята в виде Q(x) = |h(x)|.

Содержание раздела

---