Вороновский Г. - Генетические алгоритмы, искусственные нейронные сети
Настоящая брошюра подводит итоги выполнения первого этапа научного проекта "Применение эволюционных методов математического моделирования в управлении объектами энергетики ", выполняемого совместно Харьковским государственным политехническим университетом и Харьковской ТЭЦ5 при поддержке РоссийскоАмериканского Консорциума по Генетическим Алгоритмам. Проект нацелен на поиск новых концептуальных решений интеллектуальной системы управления современным энергогенерирующим предприятием, первый же его этап был направлен на разработку на базе генетических алгоритмов программного обеспечения для синтеза нейросетевых компонент будущей системы.
Приняв решение опубликовать полученные на протяжении 1995 96 гг. результаты, мы поставили перед собой цель донести до широкого читателя ключевые идеи и эвристические приемы, используемые в эволюционном моделировании, продемонстрировать эффективность новых вычислительных технологий для решения задач искусственного интеллекта. Стремление к предельной простоте и лаконичности изложения побудило нас структурировать брошюру на две части основной раздел, излагающий методические основы подходов, и Приложения, имеющие скорее справочный характер.
Чтобы упростить читателю первые шаги в самостоятельном моделировании искусственных нейронных сетей, мы снабдили брошюру результатами синтеза нейроэмуляторов и нейроконтроллеров для тестового динамического объекта, описав подробно в Приложениях структуру и параметры сетей.
Пользуясь случаем, мы хотели бы выразить благодарность профессору Эрику Гудману, директору РоссийскоАмериканского Консорциума по Генетическим Алгоритмам, за его постоянное внимание к нашим исследованиям в области генетических алгоритмов и всемерную информационную и консультативную помощь в осуществлении проекта.
СПИСОК УСЛОВНЫХ ОБОЗНАЧЕНИЙ И СОКРАЩЕНИЙ
аи Ьі левая и правая границы области допустимых значений i-той переменной проектирования;
$=(Ai A2 A3 Al) хромосома;
%(t)=($1(t),...,$M(t)) текущая популяция генотипов;
c координаты центра активационной функции;
D желаемые выходы сети (выходной шаблон); е ошибка на выходе сети;
E среда, противостоящая адаптивной системе;
H размер скрытого слоя сети;
I реакция среды, противостоящей адаптивной системе;
J функционал качества системы управления; k коэффициент усиления осциллятора;
K количество скрытых слоев сети;
L количество генов в хромосоме;
M размер популяции;
N размерность пространства переменных проектирования, представленных в вещественном виде;
Рі^Р вероятность применения генетических операторов;
Q размер тренировочного набора шаблонов;
поисковое пространство вещественных чисел;
S взвешенная сумма входных сигналов нейрона; s оператор Лапласа;
t показатель времени (непрерывный или дискретный);
T период колебаний осциллятора; ur сигнал задания; и сигнал управления;
V размер входного слоя сети; wi синаптический вес нейрона; w0 смещение нейрона;
W передаточная функция объекта; x=(Xi ,x2,.. .xN) вектор переменных проектирования; x=(x1,x2) переменные состояния в уравнении динамического объекта управления;
~ переменная состояния нейроэмулятора динамического объекта; X=(XbX2, Xy) вектор входных сигналов сети;
X = (X! , X2,..., Xy) входной шаблон; у выходной сигнал нейрона;
Y = (Y1,Y2,...,Yz ) вектор фактических значений выходных сигналов
сети;
z размер выходного слоя сети;
а гиперкуб, на котором осуществляется решение задачи комбинаторной оптимизации;
А оператор задержки;
Ф интерполяционная матрица;
^($ftj) приспособленность особи;
)!(?) средняя по текущему поколению популяции приспособленность особей;
5j ширина окна активационной функции j-того нейрона; т репродуктивный план Холланда;
'D(t)=(p.1(t),...,pM(t)) вектор приспособленностей особей популяции; ще Q генетические операторы;
Е тренировочный набор шаблонов;
Z параметр осциллятора;
АОР алгоритм обратного распространения (ошибки);
ГА генетический алгоритм;
ИНС искусственная нейронная сеть;
НК (NC) нейроконтроллер (neurocontroller);
НЭ (NE) нейроэмулятор (neuroemulator);
ОУ объект управления;
САУ система автоматического управления;
RBF-сеть трехслойная нейронная сеть с радиально-симметричной активационной функцией нейронов скрытого слоя;
XOR логическая функция исключающее ИЛИ.
ВВЕДЕНИЕ. О РАЗЛИЧНЫХ ТОЛКОВАНИЯХ ТЕРМИНА ИНТЕЛЛЕКТУАЛЬНОСТЬ В УПРАВЛЕНИИ
В последние годы среди специалистов в области теории автоматического управления наметился очевидный подъем интереса к новым нетрадиционным (то есть сформировавшимся вне рамок классической парадигмы, базирующейся на аппарате интегро-дифференциального исчисления) подходам, объединенным общей целью интеллектуализации систем управления. Наверное, трудно даже перечислить все те классификационные признаки, по которым эти подходы разнятся между собой, но одной из основных граней различия является то, что именно положено в основу концепции интеллектуализации формализованные каким-либо образом знания человека об объекте управления (ОУ), либо свойственные человеку приемы мышления, посредством которых он изучает окружающий мир и подчиняет его своим интересам.
К первой группе подходов можно отнести, например, жестко детерминированные экспертные системы, а также более гибкие системы управления на базе нечеткой (фаззи) логики (fuzzy logic). Второй подход реализуется в рамках эволюционных методов моделирования, под которыми мы подразумеваем генетические алгоритмы (ГА) и искусственные нейронные сети (ИНС).
ИНС сегодня это не столько совокупность заимствованных из нейрофизиологии моделей параллельных вычислительных структур, сколько арена борьбы идей о природе интеллекта. Если первый этап становления ИНС можно охарактеризовать как попытку синтезировать из набора сравнительно просто функционирующих нейронов некоторую упорядоченную структуру, способную выполнять сложные нелинейные преобразования вход-выход, то сейчас, по мере достижения успеха в решении задач первого этапа, передний фронт исследований перемещается в область психологии, когнитивных наук.
Задача настоящего момента состоит в том, чтобы понять, какие сверхструктуры нейронов и как могут моделировать элементарные акты мыслительной деятельности, а затем воплотить эти принципы в работу систем управления.
Мышление человека невозможно вне языка. Все явления внешнего мира нашли отражение в языке в виде категорий. Слова представляют собой не просто наборы звуков, за каждым из них стоят какие-то конкретные, но достаточно общие представления. Изучая мир, мозг накапливает информацию, упорядочивает ее и далее происходит то, что психологи называют когнитивным сжатием.
Эмпирические знания преобразуются в компактную абстрактную форму, удобную для оперирования, которая, тем не менее, несет в себе наиболее типические и важные в ракурсе решаемой индивидом практической задачи черты объекта.
Поскольку ясно, что кроме нейронов никаких других операционных единиц, участвующих в обработке информации, в мозге нет, логично предположить, что за каждым представлением, образом мира стоит конкретный фрагмент нейронной сети мозга. Создать образ объекта (или скорректировать уже имеющийся) означает тогда натренировать этот фрагмент так, чтобы его реакции на возбуждение не отличались от реакций объекта, известных из жизни.
При этом сеть должна научиться хранить опыт общения с объектом не в виде хронологически или по какому-то другому принципу упорядоченных эпизодов, а в виде собственной структуры, то есть непосредственно послойной архитектуры и сил синаптических связей между нейронами.
Может быть, именно таким путем у индивида складывается внутренняя, свойственная только ему, картина мира, образы которой помогают осознать свое положение в мире, а также прогнозировать дальнейший ход событий. Человек ретроспективно "проигрывает" в голове прошлое и проецирует настоящее на будущее не только тогда, когда играет в шахматы.
Знания о мире, а попросту говоря, прежний опыт составляет основу виртуальной реальности, существующей в нашем сознании как отражение внешнего мира. Именно умение мысленно эмулировать мир, оперировать его образами и дает нам возможность планировать свое поведение, предвидеть события и ориентироваться в пространстве потенциальных возможностей.
То, что мы попытались сделать в настоящей работе, это продемонстрировать исключительно высокий потенциал сочетания двух вычислительных технологий ИНС и ГА для решения задач синтеза интеллектуальных систем управления. С одной стороны, наш интерес к ГА обусловлен их высокой эффективностью при решении задач глобальной оптимизации вообще и как к потенциальной процедуре тренировки нейронной сети, в частности. Действительно, никто сегодня не отрицает, что многие широко известные техники тренировки (Backpropagation, RBF-сети) являются существенно локальными со всеми вытекающими отсюда последствиями, поэтому в этом отношении ГА не знает конкурентов.
С другой стороны, интригующим представляется само сочетание ГА и ИНС. Оба направления относятся к эволюционному моделированию и как бы бросают вызов методам теории автоматического управления, обещая решить традиционные задачи, не привлекая такие базовые понятия классической парадигмы как интеграл, дифференциал, динамическое звено и т. п.
Базируясь на приведенных выше общих рассуждениях, нам удалось синтезировать нейросетевую модель системы управления, которая не только умеет строить внутренние представления о внешнем мире, прогнозировать поведение объекта управления, но также обладает способностью генерировать оптимальное управление в соответствии с требованиями эталонной модели.
ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
По своей сути процессы адаптации являются оптимизационными процессами ...
Дж. Холланд, Предисловие к первому (1975) изданию Adaptation in natural and artificial systems.
Пятнадцать лет должны были бы расставить все по своим местам и охладить пыл. Однако вопреки или благодаря этому, я все еще нахожу Предисловие к изданию 1975 года удивительно уместным. Единственное изменение, которое я бы внес, это сделать большее ударение на совершенствовании и меньшее на оптимизации.
Работа над более сложными адаптивными системами, например, экологическими, убедила меня, что их поведение не описывается так уж хорошо траекториями вокруг глобальных оптиму-мов. Наоборот, соревнование между компонентами системы, направленное на подавление ближайших конкурентов, определяет общее поведение.
Дж. Холланд.
Предисловие ко второму (1992) изданию Adaptation in natural and artificial systems.
Современная библиография по генетическим алгоритмам давно перевалила за 9000 наименований и продолжает непрерывно увеличиваться. Однако, несмотря на такое обилие литературы, довольно трудно точно сформулировать, чем именно они являются квинтэссенцией эволюционных перестроек в природных популяциях организмов, универсальным средством описания адаптаций в популяциях искусственных объектов, или мощной поисковой процедурой с претензиями на решение задач глобальной оптимизации.
Мы намеренно начали этот раздел с сопоставления двух замечаний Дж. Холланда по поводу адаптации и оптимизации, сделанных им в предисловиях к первому и второму изданиям его знаменитой книги [1], положившей начало процессу распространения генетических алгоритмов в научных сообществах. Правда, генетическими они стали называться позднее, ав 1975 году Холланд называл их репродуктивными планами (reproductive plan) и рассматривал прежде всего как алгоритмы адаптации.
Но то смещение акцентов в трактовке понятия адаптация, о котором он как бы вскользь говорит в предисловии 1992 года, очень точно, на наш взгляд, передает то состояние замешательства, которое мы ощущаем и сегодня, пытаясь, с одной стороны, дать достаточно общее и непротиворечивое определение адаптации, а с другой стороны, разграничить понятия адаптации и оптимизации, адаптации и эволюции, адаптации и обучения.
При дальнейшем изложении основных идей ГА мы не будем придерживаться стиля книги Холланда, а подойдем к ним как к процедуре глобальной оптимизации. Эта, хотя и несколько упрощенная по сравнению с холландовской, трактовка ГА вызвала сильный резонанс в литературе, и как показало время, вполне обоснованно.
По большому счету, почти два десятилетия исследований ГА на тестовых многоэкстремальных функциях ушли на доказательство именно этой грани могущества ГА, оставив в некоторой тени их выдающиеся адаптивные способности.
Итак, ГА базируются на теоретических достижениях синтетической теории эволюции, учитывающей микробиологические механизмы наследования признаков в природных и искусственных популяциях организмов, а также на накопленном человечеством опыте в селекции животных и растений.
Методологическая основа ГА зиждется на гипотезе селекции, которая в самом общем виде может быть сформулирована так: чем выше приспособленность особи, тем выше вероятность того, что в потомстве, полученном с ее участием, признаки, определяющие приспособленность, будут выражены еще сильнее. Поскольку ГА имеют дело с популяциями постоянной численности, особую актуальность здесь наравне с отбором в родители приобретает отбор на элиминирование. Стратегия элиминирования, призванная ответить на вопрос От каких особей мы можем безболезненно отказаться? составляет не менее важную компоненту современных ГА, чем стратегия отбора в родительскую группу.
Чаще всего особи, обладающие низкой приспособленностью, не только не участвуют в генерации нового поколения, а элиминируются из популяции на текущем дискретном шаге (эпохе) эволюции.
Впрочем, сказанное справедливо не только для ГА, а для любого численного метода оптимизации. Сама идея оптимальности, как верно подмечено в [3], пришла в науку из биологии.
Однако далеко не всегда мы отдаем себе отчет в том, сколь многие методические приемы оптимального проектирования имеют корни в селекционной практике и являются примером нашего не всегда осознанного подражания Природе.
Небезынтересно по этому поводу мнение другого ныне здравствующего классика ГА, Кеннета Ди Янга, внесшего огромный личный вклад в развитие ГА как самостоятельного научного направления. В [2] он пишет: ...легко впасть в заблуждение, воспринимая сами ГА как алгоритмы оптимизации, а затем удивляться и/или испытывать разочарование, когда они терпят неудачу в поиске ‘очевидного’ оптимума в определенном поисковом пространстве. Мое предложение по поводу того, как избежать такого самообмана, заключается в том, чтобы думать о ГА как о (в высшей степени) идеализированном моделировании природного процесса и как о процедуре, воплощающей цели и задачи (если таковые вообще существуют) этого природного процесса.
Я не уверен, найдется ли кто-нибудь, готовый ответить на вопрос, каковы цели и задачи эволюционных систем; однако, по правде говоря, такие системы вообще не воспринимаются как оптимизаторы функций....
Убедиться в справедливости сказанного не трудно, если попытаться взглянуть на процедуру численной оптимизации через призму гипотезы селекции (см. Рис.2).
Итак, обыкновенно проектирование начинают с формирования в поисковом пространстве области допустимых значений переменных и выбора в ней некоторых пробных точек.
Далее итеративно выполняют следующие действия. Сначала при помощи математической модели устройства производят отображение точек из поискового пространства на пространство критериев, что позволяет составить представление о рельефе поверхности критериев.
Затем на основании полученной информации и в соответствии с выбранной поисковой стратегией осуществляют некоторые манипуляции с координатами точек в пространстве переменных, завершающиеся генерацией координат новых пробных точек.
Очерчивая в общих словах эту знакомую всем цепочку, отметим явно выраженный параллелизм между заложенной в ней идеологией поиска экстремума и тем, как решаются подобные по содержанию задачи в Природе, при адаптации популяций организмов к факторам окружающей среды.
Рис. 2. Циклическая структура процедуры численной оптимизации характеристик проекта
Большинство эвристических поисковых стратегий представляют собой довольно очевидные логические решающие правила, выведенные путем обобщения реального или умозрительного опыта обитания в трехмерном пространстве. Например, представим себе, что ночь застала нас врасплох и нам предстоит без фонарика двигаться по пересеченной местности, например, взобраться на вершину пологого холма.
Ясно, что взяв в руки палку и ощупывая ею ближайшее окружение, мы получим требуемую информацию о локальном рельефе и будем двигаться в том направлении, в котором местность повышается, но не наоборот. Правильный выбор направления движения и величины шага гарантирует нам быстрый успех, если, конечно, поверхность холма гладкая, а не ухабистая.
Действительно, практикуемый способ описания технических объектов при помощи векторов переменных проектирования подразумевает символьное кодирование информации об объекте. Вектор переменных даже не чертеж, то есть глядя на него и не зная правил кодирования, невозможно составить представление об объекте. В определенном смысле можно утверждать, что категория "вектор переменных проектирования" играет в технике ту же роль, что и категория "генотип" в биологии.
Группируя ключевые параметры объекта в вектор переменных, мы, по существу, придаем им статус генетической информации. Именно генетической, потому что, с одной стороны, ее достаточно, для того, чтобы построить сам объект (гипотетически вырастить его), а во-вторых, она служит исходным материалом при генерации генотипов объектов следующего поколения.
А ведь именно такой смысл генотипов потомков имеют координаты упоминавшихся новых пробных точек. Подобно тому, как в Природе скрещивание организмов осуществляется на генетическом уровне, в процедуре оптимизации координаты новых пробных точек получаются как результат манипулирования координатами старых.
Причем, и здесь незримо присутствует гипотеза селекции в качестве родительских всегда выступают лучшие в фенотипическом отношении, а не произвольные точки (особи) из популяции потенциальных решений, неудачные же решения отбрасывают на текущем шаге (можно считать, что они вымирают).
Здесь мы подходим, наконец, к тому, что именно отличает ГА на фоне других численных методов оптимизации.
ГА заимствуют из биологии:
- понятийный аппарат;
- идею коллективного поиска экстремума при помощи популяции особей;
- способы представления генетической информации;
- способы передачи генетической информации в череде поколений (генетические операторы);
- идею о преимущественном размножении наиболее приспособленных особей (речь идет не о том, даст ли данная особь потомков, а о том, сколько будет у нее потомков).
Представление генетической информации
Подобно тому, как природный хромосомный материал представляет собой линейную последовательность различных комбинаций четырех нуклеотидов (А аденин, Ц цитозин, Т тимин и Г гуанин), вектора переменных в ГА также записывают в виде цепочек символов, используя двух-, трех- или четырехбуквенный алфавит. Для простоты изложения рассмотрим случай бинарного кодирования, используемый при моделировании эволюции гаплоидных популяций.
Итак, будем считать, что каждая переменная Xj кодируется определенным фрагментом хромосомы, состоящим из фиксированного количества генов (см. рис. 3).
Все локусы хромосом диаллельны то есть в любой позиции фрагмента может стоять как ноль, так и единица. Рядом стоящие фрагменты не отделяют друг от друга какими-либо маркерами, тем не менее, при декодировании хромосомы в вектор переменных на протяжении всего моделируемого периода эволюции используется одна и та же маска картирования.
Рис. 3. Простейшая маска картирования хромосомы, определяющая план распределения наследственной информации по длине хромосомы
Хотя мы постоянно говорим о декодировании, на самом деле, прямая операция, понимаемая как операция кодирования вектора переменных x в хромосому в ГА не применяется. Хромосомы генерируются случайным образом, путем последовательного заполнения разрядов (генов), сразу в бинарном виде, и всякие последующие изменения в популяции затрагивают сначала генетический уровень, а только потом анализируются фенотипические последствия этих изменений, но никогда не наоборот.
В принципе, для декодирования генетической информации из бинарной формы к десятичному виду подходит любой двоично-десятичный код, но обычно исходят из того, что она представлена в коде Грея. Таблица 1 воспроизводит в полном объеме процедуру декодирования фрагмента хромосомы в проекцию вектора переменных Xj.
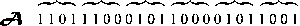
| Таблица 1 Декодирование фрагментов хромосом в проекции вектора переменных |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Из таблицы хорошо видно, почему код Грея имеет явные преимущества по сравнению с двоично-десятичным кодом, который при некотором стечении обстоятельств порождает своеобразные тупики для поискового процесса. В качестве примера рассмотрим любые три рядом стоящие строки из таблицы 1, например, кодирующие сдвиг в 4, 5 и 6 единиц.
Предположим, фрагменты хромосом, стоящие в пятой строке и кодирующие число 5, принадлежат оптимальному вектору, являющемуся решением некоторой задачи, а лучшая особь из текущей популяции содержит фрагмент хромосомы из строки 4. Такая ситуация благоприятна для обоих кодов. Достаточно выполнить всего одну операцию заменить в четвертом разряде фрагмента 0 на 1 и решение будет найдено. Более интересный случай получается, если лучшая особь содержит фрагмент из строки 6. Для кода Грея эта ситуация ничуть не сложнее предыдущей замена 0 на 1 в третьем разряде опять приведет к успеху. В то же время двоично-десятичный код ставит нас в необходимость выполнить последовательно две операции заменить 1 на 0 в третьем разряде и 0 на 1 в четвертом. С какой бы из них мы ни начали, результат не приблизит нас к решению (первый вариант замены переместит нас в четвертую строку, а второй вообще в седьмую). А ведь это не самый худший пример работать с сочетаниями 3-4, 7-8, 11-12 и т. д. строк в двоично-десятичном коде еще сложнее.
