РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ НЕЙРОКОНТРОЛЛЕРА
РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ НЕЙРОКОНТРОЛЛЕРА
Объект управления инерционное звено второго порядка (8). Параметры динамического объекта: T = 0,5, ^ = 0,1.
Цель управления подавление колебательности объекта.
Закон управления: uk+1 = NC(xk, xk-1, urk ).
Дискретность управления: А = 0,1с.
\
+ wo
( n
1
i=1
У = th
Активационная функция нейронов скрытого слоя: Количество нейронов в скрытом слое: 5.
wixi
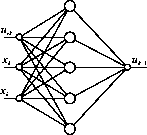
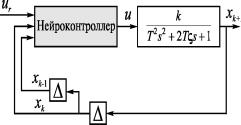
Рис. Ш.1 Огруктура нейроконтрол- Рис. П1.2 Схема работы нейроконтроллера на базе многослойного пер-
лер
а
цептрона NN351
Таблица П1.1
| Параметры нейроконтроллера |
| Параметр |
Номер нейрона скрытого слоя |
Выходной
нейрон |
| 1 |
2 |
3 |
4 |
5 |
1 |
| Wo |
0,1989 |
-0,2478 |
0,1999 |
0,2038 |
-0,0269 |
-0,0978 |
| W1 |
0,5797 |
-0,2454 |
-0,7576 |
-0,4604 |
-0,0244 |
1,4370 |
| W2 |
-0,9609 |
0,9433 |
0,7498 |
-0,2493 |
-0,5230 |
-3,3920 |
| W3 |
0,5347 |
-0,6090 |
0,1281 |
0,8592 |
0,7810 |
-9,8827 |
| W4 |
|
|
|
|
|
5,5034 |
| w5 |
|
|
|
|
|
6,2463 |
|
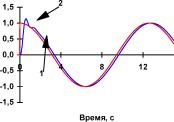
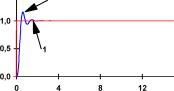
в)
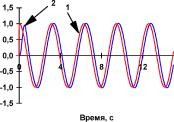
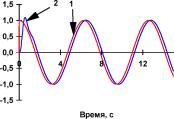
Рис. П1.3 Реакция системы управления (кривая 2) с нейроконтроллером на входное воздействие (кривая 1) в виде гармонического сигнала с единичной амплитудой и частотой а) 0; б) 0,08; в) 0,16 иг) 0,32 Гц
Для оценки параметрической чувствительности системы был введен интегральный функционал качества:
t \
J(x (t)-u
r (t ))P dt
J (х )=
1
max 0
Здесь N=3 количество экспериментов, t
max=10 c время интегрирования переходного процесса в системе, u
r ступенчатое входное задание амплитудой -1, 0 и 1. Значение функционала, полученное при оптимальной настройке нейроконтроллера, равно J=0,0235.
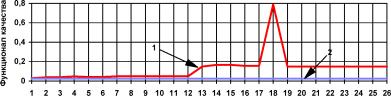
На рис. П1.4 представлен график изменения функционала качества при изменении каждого из 26 параметров нейроконтроллера в диапазоне -100 100%. Как видно, изменение любого из 26 параметров в пределах -
20 20% не приводит к существенному ухудшению качества работы сис
темы (статическая ошибка 5%, перерегулирование ~15%, 1,22 колебания переходного процесса). Такой допустимый диапазон дрейфа параметров от заданного оптимального значения вполне может быть обеспечен при использовании стандартных полупроводниковых приборов.
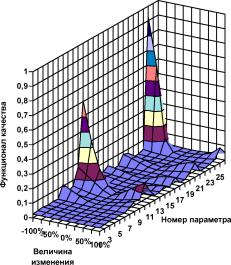
Рис. П1.4. Зависимость качества работы системы управления от изменения параметров нейроконтроллера
Тем не менее, из рис. П1.4 видно, что разные параметры нейронной сети оказывают различное влияние на эффективность ее работы. Так, изменение параметров номер 10, 11 и 24 (веса первой и второй связей третьего нейрона скрытого слоя и вес связи с ним выходного нейрона, соответственно) вызывает наибольшие нарушения в работе нейроконтроллера.
В то же время 100%ое изменение 4, 17 и 22 параметров (вес третьей связи первого и смещение пятого нейронов скрытого слоя и вес первой связи выходного нейрона, соответственно) практически не сказывается на эффективности управления.
На рис. П1.5 представлено семейство переходных функций системы управления при изменении значения 11го параметра нейроконтроллера в диапазоне от -100% до 100%. Изменения в пределах 50% оказывают влияние в основном на статическую ошибку, большие же изменения нарушают также и динамические свойства системы, увеличивая колебательность. Семейство, представленное на рис.
П1.6, показывает, что изменение 17го параметра сказывается лишь на статической ошибке системы.
Рис. П1.6. Переходные функции системы управления при различных изменениях 17го параметра нейроконтроллера
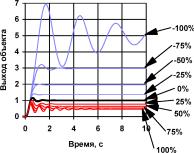
Рис. П1.5. Переходные функции системы управления при различных изменениях 11го параметра нейроконтроллера
Помимо оценки изменений, вызванных варьированием значений настроечных параметров нейроконтроллера, большой интерес представляет анализ влияния на его работу аварий в виде обрыва межслойных связей, выходе из строя нейронов или обрыва обратных связей всей системы управления.
На рис. П1.7 представлен график изменения функционала качества работы системы управления при последовательном, в произвольном порядке, выходе из строя межслойных соединений (сигналы от поврежденных связей считаются нулевыми).
Благодаря тому, что информация передается и обрабатывается нейронами параллельно, при обрывах межслойных связей наблюдается не резкая утеря, а постепенная деградация работоспособности системы.
Распределение функций между отдельными нейронами скрытого слоя можно выяснить, сравнив переходные процессы в системе при их отключении (на выходе нейрона нулевой сигнал). Рис. П1.8 показывает, что
ключевая роль в данном нейроконтроллере принадлежит третьему нейрону скрытого слоя. При его аварии (рис.
П1.8в) сеть теряет способность различать входной сигнал управления ur. (т. е. его амплитуду и полярность), и нейроконтроллер выдает постоянный сигнал. Четвертый и пятый скрытые нейроны определяют, прежде всего, динамические свойства нейроконтроллера , так как при их поломке (рис.
П1.8г,д) резко увеличивается колебательность системы. Роль первого и второго нейронов, очевидно, изза некоторой избыточности структуры нейроконтроллера менее значительна, и их выход из строя заметен только при определенных величинах входного сигнала ur (рис. П1.8а,б).
Таким образом, отдельные нейроны в сети не только делят между собой процесс вычисления, но и выполняют различные функции.
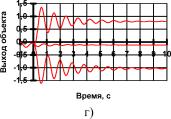
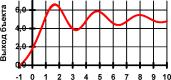
Рис. П1.8. Переходные процессы в системе при подаче на вход сигнала задания м
г=1,0,1 с отключенными а) 1м, б) 2м, в) 3м, г) 4м, д) 5м нейронами скрытого слоя
Другой достаточно часто встречающейся аварийной ситуацией является обрыв обратных связей в системе управления. На рис. П1.9 представлены переходные процессы при различных вариантах аварий, при этом, как
и ранее, считается, что сигналы в поврежденных линиях нулевые. Как показывают эксперименты (рис. П1.9а), в случае обрыва обратной связи по выходному сигналу x
k система сохраняет динамические свойства объекта управления, но резко ухудшается ее статическая характеристика.
Обрыв обратной связи по задержанному выходному сигналу xk-1 (рис. П1.9б) приводит к возникновению в системе устойчивого колебательного процесса с частотой, в три раза превышающей собственную частоту объекта управления. В случае аварии в обоих каналах обратной связи по xk и xk-1 (рис.
П1.9в) нейроконтроллер превращается в линейный усилитель с коэффициентом усиления 3,8.
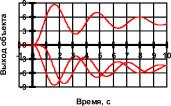
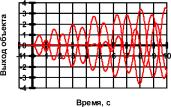
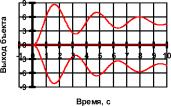
Рис. П1.9. Переходные процессы в системе при подаче на вход сигнала задания u
r=-1,0,1 с оборванными обратными связями: а) по x
k; б) по x
k-1; в) одновременно по x
k и x
k-1
Таким образом, анализ эффективности работы нейроконтроллера при различных параметрических возмущениях доказывает возможность его аппаратной реализации и использования в реальных системах автоматического управления.
ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА БЕЗ ЗАТУХАНИЯ
Параметры динамического объекта T = 0,5, ^ = 0. Закон предсказания: хк+1 = NE(~k,~к ,uk ). Дискретность шага предсказания: А = 0,05 с. Количество нейронов в скрытом слое: 29.
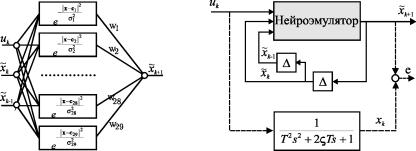
Рис. П2.2 Схема обучения нейроэмулятора
Рис. П2.1 Структура нейроэмулятора на базе RBFсети NN3291
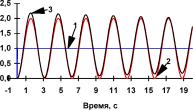
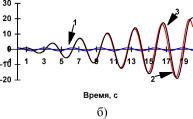
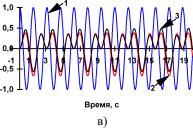
Рис. П2.3 Реакция динамического объекта (кривая 2) и его нейроэмулятора (кривая 3) на тестовые входные воздействия (кривая 1) в виде: а) единичного положительного скачка; гармонических сигналов частотой б) 0,32 Гц ив) 0,64 Гц.
Таблица П2.1
Параметры нейроэмулятора
Номер
нейрона |
Оі |
Си |
С2І |
С3і |
Wi |
| 1 |
1,32940000 |
0,13241723 |
4,00264870 |
3,69552579 |
-0,0001097 |
| 2 |
7,48650000 |
0,87195910 |
-11,884959 |
-12,633569 |
-0,1450785 |
| 3 |
3,23520000 |
-0,6425613 |
-1,1307631 |
-1,0433907 |
-0,0004277 |
| 4 |
8,75700000 |
0,42751159 |
0,43238915 |
-0,3978190 |
-0,0077664 |
| 5 |
3,28400000 |
-0,2018089 |
16,20067093 |
15,56336087 |
0,03483315 |
| 6 |
48,38740000 |
0,45964651 |
-15,708139 |
-15,589026 |
-633,17019 |
| 7 |
50,00000000 |
-0,0679447 |
14,29644381 |
13,57155420 |
-1243,6867 |
| 8 |
14,57210000 |
0,30086970 |
-16,674901 |
-16,200671 |
0,30450690 |
| 9 |
14,13230000 |
0,32749103 |
5,53452296 |
5,10459268 |
-3,2338332 |
| 10 |
24,78510000 |
0,17489940 |
0,69095922 |
0,69371846 |
-68,952788 |
| 11 |
46,97030000 |
-0,1385397 |
3,44557024 |
3,41429828 |
-6199,9877 |
| 12 |
6,80240000 |
-0,5236824 |
9,73838706 |
9,86534335 |
0,01709318 |
| 13 |
31,47980000 |
-0,1656235 |
-4,2535344 |
-3,8596768 |
581,4529719 |
| 14 |
22,39070000 |
0,93144906 |
-7,9566017 |
-8,7541562 |
-44,303714 |
| 15 |
27,91250000 |
-0,0304202 |
-10,353410 |
-9,8316845 |
-101,06493 |
| 16 |
48,04540000 |
0,40019947 |
-3,5018439 |
-3,7229122 |
19822,83699 |
| 17 |
37,88120000 |
0,65216708 |
4,37062760 |
3,65904987 |
418,9776593 |
| 18 |
36,07320000 |
-0,9718113 |
4,04787287 |
5,60667437 |
1100,885665 |
| 19 |
49,90230000 |
-0,3274910 |
-5,5345229 |
-5,1045927 |
-485,76029 |
| 20 |
45,30890000 |
0,91712343 |
-0,6611883 |
-2,1625168 |
-6329,2657 |
| 21 |
7,09560000 |
-0,3530623 |
-2,4496238 |
-1,7834204 |
0,03537472 |
| 22 |
34,46060000 |
-0,3021165 |
-3,3874906 |
-2,6744797 |
1831,77891 |
| 23 |
48,43630000 |
0,19310298 |
-0,5359441 |
-0,4692599 |
-40511,918 |
| 24 |
44,38040000 |
-0,6143198 |
0,89066105 |
0,89738176 |
4872,731958 |
| 25 |
11,64010000 |
-0,0023824 |
11,68965487 |
11,10051653 |
-1,5858362 |
| 26 |
0,35210000 |
-0,7376198 |
3,31480182 |
3,50859631 |
-0,0004036 |
| 27 |
49,26700000 |
0,31347508 |
2,58143453 |
2,15959841 |
29301,96984 |
| 28 |
32,06610000 |
-0,9139232 |
-1,1400909 |
-0,5133197 |
-1674,9079 |
| 29 |
45,60210000 |
0,36572367 |
9,68191210 |
8,59445512 |
-662,99532 |
РЕЗУЛЬТАТЫ СИНТЕЗА И АНАЛИЗ ПАРАМЕТРИЧЕСКОЙ ЧУВСТВИТЕЛЬНОСТИ ЭМУЛЯТОРА КОЛЕБАТЕЛЬНОГО ЗВЕНА С ЗАТУХАНИЕМ
Параметры динамического объекта T = 0,5, q = 0,1. Закон предсказания: хк+1 = NE(~k,xk-1,ык).
Шаг предсказания: А = 0,05 с.
Глубина предсказания: 20 с.
Количество нейронов в скрытом слое: 8.
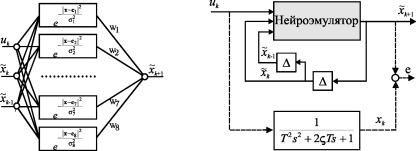
Рис. П3.1 Структура нейроэмулятора на Рис. П3.2 Схема обучения нейроэмуля-базе RBFсети NN381 тора
Таблица П3.1.
| Параметры нейроэмулятора |
Номер
нейрона |
^І |
си |
С2І |
C3i |
Wi |
| 1 |
87,59170000 |
0,99974055 |
1,09053782 |
1,09603289 |
-17227,406 |
| 2 |
94,91950000 |
0,43480822 |
0,58749893 |
0,37194684 |
47788,67779 |
| 3 |
77,43060000 |
0,54402968 |
2,90636127 |
2,58175994 |
912,5565002 |
| 4 |
100,0000000 |
-0,6062078 |
-0,3264445 |
-0,3396649 |
14624,26589 |
| 5 |
88,27570000 |
0,85952439 |
-1,7761579 |
-1,9766618 |
-3270,5978 |
| 6 |
53,20030000 |
-0,6581776 |
-2,5003728 |
-2,0844048 |
131,1890993 |
| 7 |
99,41380000 |
0,21871813 |
-1,5809023 |
-1,6124321 |
4349,455315 |
| 8 |
99,90230000 |
-0,2195961 |
-0,0883838 |
-0,0166504 |
-47309,744 |
|
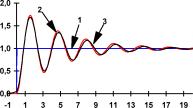
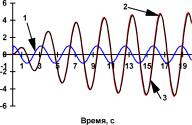
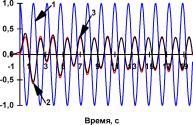
Рис. ПЗ.З Реакция динамического объекта (кривая 2) и его нейроэмулятора (кривая 3) на тестовые входные воздействия (кривая 1) в виде а) единичного положительного скачка, гармонического сигала частотой б) 0,32 Гц ив) 0,64 Гц
Так как целевая функция, использовавшаяся генетическим алгоритмом при обучении эмулятора, включала помимо ошибки в воспроизведении тренировочных шаблонов штраф, пропорциональный количеству узлов в скрытом слое, то в первом приближении можно считать, что описываемая сеть обладает минимальной структурой.
Представленный ниже анализ влияния даже чрезвычайно малых искажений оптимального вектора настроек выявил очень высокую параметрическую чувствительность данного решения. Чем ее можно объяснить, пока не ясно. Мы думаем, три фактора могли сыграть в этом деле существенную роль. Вопервых, возможно, не стоило стремиться к минимизации количества скрытых нейронов. Вовторых, отсутствие в процессе синтеза сети контроля за соотношением расстояний между центрами и шириной окон активационных функций. Наконец, в третьих, применение специфического локального ускорителя ГА, использующего процедуру обращения матрицы. Как бы ни было, это, безусловно, проблема, без решения которой говорить об аппаратной реализации эмулятора не приходится.
А) Изменение ширины окна активационной функции.
Реакции эмулятора на ступенчатое возбуждение, соответствующие различным искажениям параметра о
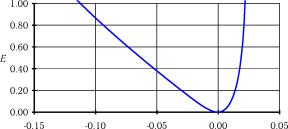
4, демонстрирует рис. П3.4. Кривая 3 соответствует изменению параметра на 0,01% от оптимальной величины; при этом e=3,84- 10-2. Кривая 4 соответствует изменению параметра на 0,1%; при этом e=8,67- 10-1. Кривая 5 соответствует изменению параметра на 0,2%; при этом e=1,22- 104. Зависимость среднеквадратичной ошибки от изменения параметра о
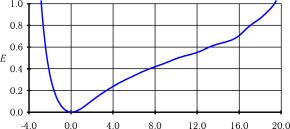
4 приведена на рис. П3.5.
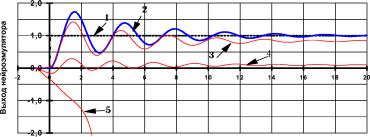
Рис. П3.4. Влияние искажения оптимальной настройки ширины окна активационной функции на способность нейросети эмулировать тестовый динамический объект. Кривая 1 входной ступенчатый сигнал; 2 эталонная реакция объекта^ выход сети при g
4=99,99; 4 выход сети при g
4=99,90; 5 выход сети
при g
4=99,80
.
В) Изменение координаты центра активационной функции c
3,
8.
Работа эмулятора демонстрируется на рис. П3.6. Кривая 3 соответствует отклонению параметра на 0,1% от оптимального значения; при этом e=4,61- 10-1. Кривая 4 соответствует отклонению параметра на 1%; при этом e=1,87. Кривая 5 соответствует отклонению параметра на 4%; при этом e=12,5. Зависимость среднеквадратичной ошибки от изменения параметра c
3,
8 приведена на рис. П3.7.
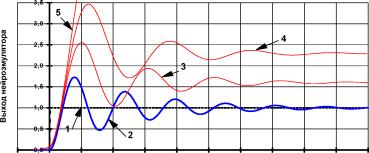
Рис. П3.6. Влияние искажения оптимальной настройки координаты центра активационной функции на способность нейросети эмулировать тестовый динамический объект. Кривая 1 входной ступенчатый сигнал; 2 эталонная реакция объекта; 3 выход сети при c
3,
8=-0,01702; 4 выход сети при c
3,
8=-0,0172;
5 выход сети при c
3,
8=-0,0174.
С) Изменение синаптического веса выходного нейрона.
Работа эмулятора демонстрируется на рис. П3.8. Кривая 3 соответствует изменению наибольшего по модулю параметра w
2 на 10-5%; при этом e=1,94- 10-1. Кривая 4 соответствует изменению параметра w
2 на 10-4%; при этом e=16,71. Кривая 5 соответствует изменению наименьшего по модулю параметра w
6 на 0,007%; при этом e=1,54. Кривая 6 соответствует
изменению параметра w
6 на 0,1%; при этом e=80,15. Зависимость среднеквадратичной ошибки от изменения параметра w
2 приведена на рис. П3.9.
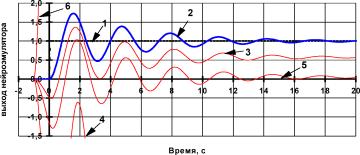
Рис. П3.8. Влияние искажения оптимальной настройки синаптического веса выходного нейрона на способность нейросети эмулировать тестовый динамический объект. Кривая 1 входной ступенчатый сигнал; 2 эталонная реакция объекта; 3 выход сети при w
2=47788,673; 4 выход сети при w
2=47788,637; 5 выход сети при w
6=131,180; 6 выход сети при w
6=131,280.
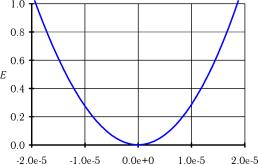
| Изменение параметра сети, % |
Рис.
П3.9. Зависимость среднеквадратичной ошибки от изменения параметра w2
ЭМУЛЯТОР КОЛЕБАТЕЛЬНОГО ЗВЕНА С СИЛЬНЫМ ЗАТУXАНИЕМ
Параметры динамического объекта: T = 0,5, q = 0,5. Закон предсказания: хк+1 = NE(~k,~k_г,uk)
Шаг предсказания: А = 0,05 с.
Глубина предсказания: 20 с.
Количество нейронов в скрытом слое: 10.
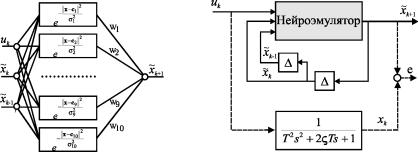
Рис. П4.1 Структура нейроэмулятора на Рис- П4-2 Схема [учения нейроэмуля-базе RBF-сети NN3-10-1 тора
Таблица П4.1
| Параметры нейроэмулятора |
Номер
нейрона |
^і |
си |
С2І |
С3і |
Wi |
| 1 |
99,70690000 |
0,72284891 |
1,01750381 |
1,01039823 |
-106163,87 |
| 2 |
96,48270000 |
0,40865195 |
0,41362282 |
0,41407195 |
10388,48445 |
| 3 |
100,0000000 |
-0,5647115 |
-0,3332744 |
-0,3094531 |
63732,71896 |
| 4 |
5,52140000 |
-0,7225222 |
-0,6242014 |
-0,6140152 |
0,27695870 |
| 5 |
25,06190000 |
-0,7191648 |
-1,1053778 |
-1,1107858 |
-130,64725 |
| 6 |
33,56210000 |
-0,5864175 |
-1,0888907 |
-1,1048114 |
235,1114704 |
| 7 |
100,0000000 |
0,57451998 |
0,71946869 |
0,64836559 |
156186,9946 |
| 8 |
99,90230000 |
-0,7685449 |
-0,1323748 |
-0,0691282 |
-78653,683 |
| 9 |
0,05000000 |
-0,6010585 |
-0,6974816 |
-0,6241169 |
0,00000881 |
| 10 |
100,0000000 |
0,91759329 |
-0,2635411 |
-0,2578979 |
-45608,521 |
|
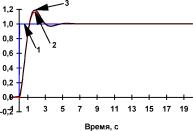

a) б)
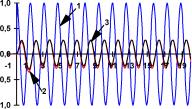
Рис. П4.3 Реакция динамического объекта (кривая 2) и его нейроэмулятора (кривая 3) на тестовые входные воздействия (кривая 1) в виде а) единичного положительного скачка, гармонического сигала частотой б) 0,32 Гц ив) 0,64 Гц
ВИРТУАЛЬНЫЙ ТРАКТ УПРАВЛЕНИЯ НА БАЗЕ НЕЙРОЭМУЛЯТОРА
Параметры нейроэмулятора представлены в Приложении 3. Дискретность управления А1 = 0,1 с, шаг предсказания А 2 = 0,05 с. Закон управления: uk+1 = NC(~k, ~k_1, urk ).
Ё wixi + w0
Активационная функция скрытых нейронов y = th Количество нейронов в скрытом слое: 10.
i=1
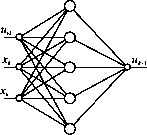
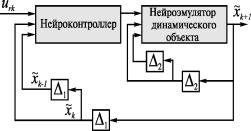
Рис. П5.2 Структура нейроконтроллера на базе многослойного перцептрона NN 3-10-1
Рис. П5.1 Схема виртуального тракта интеллектуальной САУ
Таблица П5.1
Смещение и синаптические веса скрытых нейронов нейроконтроллера
Номер
нейрона |
W0 |
W1 |
W2 |
W3 |
| 1 |
-7,6329 |
-1,9880 |
-6,4170 |
9,1198 |
| 2 |
8,6352 |
0,3241 |
4,7970 |
-0,0922 |
| 3 |
-6,2498 |
0,2765 |
-5,2377 |
-6,5257 |
| 4 |
8,8451 |
-9,4409 |
1,1298 |
3,8790 |
| 5 |
-9,9036 |
-5,4502 |
-4,6493 |
-6,2840 |
| 6 |
-8,9538 |
-1,9490 |
1,0395 |
-7,4608 |
| 7 |
6,5257 |
-7,2655 |
4,3478 |
-8,6364 |
| 8 |
-0,0043 |
-5,0082 |
9,1430 |
-4,7250 |
| 9 |
-2,2005 |
2,4641 |
-1,5144 |
-2,5056 |
| 10 |
0,0153 |
-2,4995 |
-1,5608 |
6,2376 |
Таблица П5.2
Смещение и синаптические веса выходного нейрона нейроконтроллера
| Wo |
0,4547 |
W6 |
0,3801 |
| Wi |
-0,4762 |
W7 |
-0,3780 |
| W2 |
0,2257 |
W8 |
-0,5626 |
| W3 |
-0,2251 |
W9 |
-0,1820 |
| W4 |
-0,4920 |
Wi0 |
0,2511 |
| w5 |
0,3427 |
|
|
Рис. П5.3 и П5.4 демонстрируют работу нейроконтроллера в составе, соответственно, виртуального и прямого трактов управления интеллектуальной САУ.
Как видно, нейроконтроллер вполне успешно справляется как с нейроэмулятором, с помощью которого он был синтезирован, так и с самим динамическим объектом.
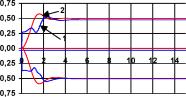
Рис. П5.3.
Выход нейроконтроллера (кривая 1) и реакция нейроэмулятора (кривая 2) на входные задания САУ ur-=-0,5;0;0,5.
Рис. П5.4.
Работа прямого тракта управления САУ при входных заданиях ur= =-0,5;0;0,5. Кривая 1 выход нейроконтроллера, кривая 2 выход тестового динамического объекта.
ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ И ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ В ИНТЕРНЕТЕ
Спектр предлагаемых Интернетом услуг настолько широк, что он в состоянии изменить весь стиль научной жизни и творчества. Интернет предоставляет уникальные каналы для получения свежайшей информации по любому интересующему вас вопросу, предлагает реальные средства приобщиться к жизни мирового научного сообщества, не покидая пределов родного города.
Впрочем, агитировать за Интернет вряд ли еще актуально, мы надеемся, что у вас есть к нему доступ, и хотели бы просто дать краткий список полезных адресов, связанных с деятельностью ГА+ИНС сообщества.
Крупнейшим хранилищем информации в области эволюционного моделирования является ENCORE (The EvolutioNary Computation REpository network) специализированная сеть, объединяющая FTP-серверы ведущих научно-исследовательских организаций и высших учебных заведений, известных своими достижениями в области ГА и ИНС. Одновременно ENCORE выступает дистрибьютором научных материалов тех учреждений, которые не имеют собственных FTP-серверов. Все узлы сети ENCORE содержат одну и ту же информацию, доступную по протоколу FTP и WWW.
В следующей таблицеце приведены адреса некоторых из WWW-узлов.
Таблица П6.1
| WWW-узлы сети ENCORE |
| |
EUNET,
Германия |
| |
Университет Гранада, Испания |
| oke/encore/ |
Институт Санта Фе,
США |
| |
Университет Альберты, Канада |
| |
Китайский университет Гонконга,
Китай |
|
Другие серверы предлагают доступ только по протоколу FTP (более доступному на сегодняшний день).
Таблица П6.2
| FTP-серверы сети ENCORE |
| ftp ://ftp.egr.msu.edu:/ pub/EC/W elcome.html |
Университет Штата Мичиган, Ист Лансинг,
США |
ftp://alife.santafe.edu:/pub/USERAREA/EC/Welcome
.html |
Институт Санта Фе,
США |
| ftp ://ftp.krl.caltech.edu:/pub/EC/W elcome. html |
Калифорнийский институт Технологий,
США |
| ftp ://ftp .cs.wayne .edu:/ pub/EC/W elcome.html |
Университет Уэйна, Детройт, США |
ftp://ftp-bionik.fb10.tu-berlin.de:/pub/EC/Wel
come.html |
Технический университет Берлина,
Г ермания |
| .polytechni que.fr:/ pub/eark/EC/W elcome. html |
Политехническая школа Пале-
зо,
Франция |
ftp://ftp.dcs.warwick.ac.uk:/pub/mirrors/EC/Welcome.
html |
Университет Уорвик, Великобритания |
| ftp://ftp.uct.ac.za:/pub/mirrors/EC/Welcome.html |
Университет Кейптауна,
ЮАР |
| ftp :// elcome. html |
Центр технического образования в Паране,
Бразилия |
|
Примечательно, что в Америке помимо издающихся в привычном виде журналов (таких специализированных журналов два - Evolutionary Computation е IEEE Transactions on Evolutionary Computation), выходит электронный журнал The Genetic Algorithm Digest. Номер объемом 4-5 страниц выходит почти еженедельно (60 раз в год), содержит дневник конференций и вообще играет роль постоянно действующего круглого стола, объединяющего почти 2000 поклонников ГА со всего мира.
Содержание раздела



































