Некоторые аналитические модели СМО
Обозначения : Н- накопитель, К - канал обслуживания, кружок - поток входных заявок, прямоугольник - ПО, ромб - поток обслуженных заявок.
В 1953 году Г. Кендалл предложил стандартные обозначения для введённых выше определений, которые и используются исследователями без изменений. Для однофазных СМО символика Кендалла выглядит следующим образом :
A / B / n / m 2.1
Где A и B входной поток и поток обслуживания соответственно ,
n число каналов, n 1,
m - ёмкость накопителя.
Потоки случайных событий могут иметь различный вид:
- М экспоненциальное распределение длительностей интервалов поступления заявок или длительностей обслуживания ( индекс М от определяющего слова марковский процесс, т.е. такой, когда поведение процесса после момента времени t зависит лишь от состояния процесса в момент времени t и не зависит от поведения до момента времени t),
- D - детерминированное распределение длительностей интервалов поступления заявок или длительностей обслуживания,
- Ек - поток Эрланга к го порядка для длительностей интервалов между приходами заявок или длительностей обслуживания,
- GI - рекуррентный поток (длительности интервалов статистически независимы и имеют одинаковое распределение),
- G - общий вид распределения.
Тогда в символах Кендалла вместо А и В подставляется символ одного из упомянутых потоков, например:
M/M/1 - экспоненциальные потоки с одним каналом обслуживания и неограниченной ёмкостью.
D/GI/5/10 - детерминированный входной поток, рекуррентный поток обслуживания, многоканальное СМО с 5 одинаковыми каналами, ёмкость накопителя 10 и т.д.
Описание любого варианта СМО на языке математики достаточно несложно, но практически малоценно, так как не отражает динамики процесса функционирования системы. Поэтому всегда существует необходимость, получив предварительные числовые ориентиры на основе аналитической модели, далее строить имитационную модель, для чего незаменим ЯИМ GPSS/H .
Некоторые аналитические модели СМО
Не будем рассматривать причины, приводящие к искажению сформулированных свойств простейшего потока, отметим только, что процесс прихода заявок подчиняются в этом случае функции распределения Пуассона, а время прихода и обслуживания описывается экспоненциальной функцией распределения. Любые другие функции распределения приведут к лучшим параметром потоков, поэтому считается, что если параметры СМО удовлетворяют условиям простейшего потока, то они наверняка обеспечат удовлетворительную работу СМО при всех других потоках.
В связи с этим в рассматриваемых далее моделях используются функции распределения Пуассона и экспоненциальные.
Распределение вероятности длительности интервалов между заявками
Пусть f(t)- плотность распределения длительностей t интервалов между любой парой смежных заявок. Определим параметр потока , как среднюю частоту появлений заявок, а 1/, как среднее значение длительности интервала, тогда
t f( t )dt = 1/ . 2.2
Например, если за дискрету времени примем 1 час, а = 4, то среднее количество поступлений равняется 15 минутам (1 / = 0.25) и наоборот, если каждые 10 минут в систему поступает одна заявка, то частота поступлений равняется 0.1 заявок в минуту.
Для стационарного потока плотность определяется как:
f ( t ) = e - t t , 2.3
такое распределение называется экспоненциальным.
Вычисляя вероятность попадания n заявок в произвольно выбранный интервал Т, приходим к распределению Пуассона:
P n ( t ) = ((t )n / n! ) e t . n = 0,1,2, 2.4
Полученные распределения отвечают всем свойствам простейшего потока.
Впредь будем полагать, что отсчёт времени начинается с момента Т 0.
Не трудно показать, что экспоненциальная функция распределения заявок и пуассоновский процесс обладают одинаковыми статистиками и их можно считать синонимами, поэтому, и принято обозначение марковский процесс или М процесс.
Распределение вероятностей длительностей обслуживания
Будем считать, что каждый канал в одно и то же время может обслуживать только одну заявку. Следующие друг за другом интервалы обслуживания независимы и имеют идентичное распределение.
Пусть плотность распределения равна g (t), тогда среднее время обслуживания равно:
T0 = t g ( t ) dt = 1 / , 2.5
где - параметр (темп) потока обслуживания.
Так, например, если за дискету времени принять 1 час, а = 5, то в течение часа прибор обслужит 5 требований и среднее время обслуживания равно 12 минутам и наоборот, если на обслуживание заявки уходит 30 минут, то темп обслуживания = 2. При расчёте среднего времени обслуживания учитывается только время занятости прибора обслуживания.
Для получения верхней границы пропускной способности канала обычно полагают, что распределение длительностей обслуживания является экспоненциальным:
G (t) = e -t при t 0, 2.6
при этом вероятность завершения обслуживания в интервале (t + t) не зависит от того, сколько времени уже потрачено на обслуживание этой заявки (пример системы, не обладающей памятью). Таким образом, если в момент t заявка уже обслуживалась, то в силу (2.6) в момент t + t вероятность того, что в этом интервале обслуживание не заканчивается:
P (t + t) e -. 2.7
Следовательно, при очень малых t, вероятность того, что обслуживание в рассматриваемом интервале не заканчивается равна:
P ( t + t )1 - , 2.8
а что заканчивается
P ( t + t ) . 2.9 Рассмотрим пример, в котором имеется возможность аналитического определения показателей эффективности функционирования СМО (М/М/1). Пусть процесс обслуживания начинается при отсутствии заявок в накопителе, тогда состояние СМО описывается следующей системой уравнений:
2.10
где Рn(t) - вероятность нахождения системы в состоянии
Вероятность нахождения в системе n заявок в момент времени (t + t) равна сумме трех вероятностей:
1) вероятности нахождения в системе n заявок в момент t, умноженной на вероятность того, что за время t в систему не поступает ни одной заявки и ни одна заявил не будет обслужена;
2) вероятности нахождения в системе (n - 1) заявки в момент t, умноженной на вероятность поступления одной заявки за время t, и ни одна заявка не будет обслужена;
3) вероятности нахождения в системе (n + 1) заявки в момент t, умноженной на вероятность ухода одной заявки, при условии не поступления ни одной заявки.
Заметим что,
Образуя разностное уравнение и переходя к пределу, получаем дифференциальные уравнения:
Найдем выражение среднего числа заявок, находящихся в накопителе, и среднего времени ожидания заявок в накопителе для стационарного состояния при загрузке
Приравняв производные по времени t к нулю, получим уравнения:
Положим n =1, тогда (1+ )p1 = p2 +
Следовательно, получим, что рn = рn(1 - ) геометрическое распределение.
Среднее число заявок в системе равно:
Среднее число заявок, находящихся в накопителе, равно:
Среднее время ожидания заявок в накопителе равно:
Среднее время пребывания в системе равно:
E{ w } = 1 /
Сведём основные операционные характеристики рассматриваемой системы с дисциплиной FCFS (FIFO) в таблицу 2.2.
Таблица 2.2 Операционные характеристики СМО
 |
 |
 |
 |
||||||
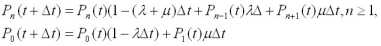
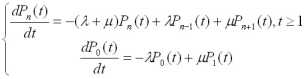
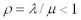
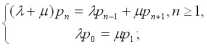
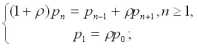
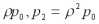
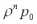
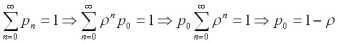
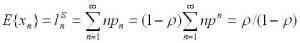
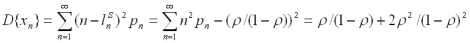
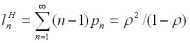
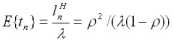
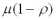
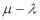
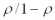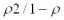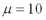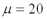| 1- | Ew | Etn | Ew | Etn | |||||
| 0.1 | 0.9 | 0.11 | 0.01 | 1 | 0.11 | 0.01 | 2 | 0.06 | 0.01 |
| 0.3 | 0.7 | 0.43 | 0.13 | 3 | 0.14 | 0.04 | 6 | 0.07 | 0.02 |
| 0.5 | 0.5 | 1.0 | 0.5 | 5 | 0.2 | 0.1 | 10 | 0.1 | 0.05 |
| 0.7 | 0.3 | 2.33 | 1.63 | 7 | 0.33 | 0.23 | 14 | 0.17 | 0.12 |
| 0.8 | 0.2 | 4.0 | 3.2 | 8 | 0.5 | 0.4 | 16 | 0.25 | 0.2 |
| 0.9 | 0.1 | 9.0 | 8.1 | 9 | 1 | 0.9 | 18 | 0.5 | 0.45 |
| 0.95 | 0.05 | 19.0 | 18.05 | 9.5 | 2 | 1.9 | 19 | 1 | 0.95 |
| 0.99 | 0.01 | 99.0 | 98.01 | 9.9 | 10 | 9.9 | 19.8 | 5 | 4.95 |
| 0.999 | 0.001 | 999.0 | 998.0 | 9.99 | 100 | 99.9 | 19.98 | 50 | 49.95 |
Рассмотрим конкретный пример использования Таблицы 2.2. Пусть дискрета времени равна 1 часу, а =0.8. Прибор простаивает в среднем 0.2 часа (12 минут), а среднее количество требований в системе равно 4. При
Возможны ситуации, когда длина очереди ограничена, если в СМО не может быть более L заявок, то длина очереди ограничена величиной L 1 и любая заявка сверх этого значения теряется, и статистическое равновесие в этом случае достигается при любом значении (Л. 2).
В данном разделе не рассмотрены другие более сложные модели использования теории массового обслуживания. Однако, следует подчеркнуть, что теория СМО прекрасно реализуется способами имитационного моделирования с использованием ЯИМ GPSS/H.
Поэтому концептуальная основа теории СМО позволяет решать сколь угодно сложные практические задачи, встречающиеся в технике, бизнесе и информатике.
Глава 3.Средство компьютерного моделирования - ЯИМ GPSS/H
Язык имитационного моделирования GPSS был создан в 1968 году фирмой IBM по заказу военно-морских сил США для моделирования сложнейших процессов снабжения флота, находящегося вдалеке от портов приписки. Поскольку тогда не существовало персональных компьютеров (датой их появления считается, по различным источникам, 1987 1988 год), первая версия GPSS предназначалась для работы в операционной среде и с техническими средствами тех времен (Л.2).
Впоследствии язык неоднократно модифицировался, появилась версия, способная работать не только в операционной системе MS-DOS и в ее эмуляциях, но и непосредственно в ОС Windows’95,98, NT, XP.
Одна из последних версий GPSS, названная GPSS/H, выпущена фирмой Wolverine Software Corporation автор James Henriksen в 1996 году, но к сожалению, пока не нашла широкого применения в России. В то же время ее отличает от старых версий множество новых положительных свойств и возможностей. Перечислим некоторые существенные достоинства:
- отсутствие собственной оболочки, что позволяет сократить время ознакомления с программой и упрощает работу во всех средах;
- наличие так называемого отладчика программ, или дебагера, что позволяет сократить и сделать более эффективным этап отладки программ;
- наличие фортраноподобных переменных (амперсант-переменных), которые позволяют значительно упростить многие операции и сделать модель более информативной для наблюдателя и удобной в работе;
- возможность управления форматом и количеством информации в файле отчета, содержащем результаты моделирования и т.д. (см. Л.1,2).
Назначение и структура GPSS/H
Назначение GPSS/H - General Purpose Simulation System, то есть общецелевая система моделирования. Это средство (ниже будут для краткости использоваться термины язык или ЯИМ) предоставляет пользователю возможность создавать и испытывать имитационные модели различных по своему физическому устройству и назначению систем.
Необходимо только, чтобы решаемая с помощью моделирования задача могла быть описана средствами теории систем массового обслуживания (которая перекрывает широкий класс задач). Строго говоря, под это определение подпадают объекты, процесс функционирования которых можно представить в виде состояний и правил перехода из одного состояния в другое, определяемых в дискретной пространственно-временной области.
Объекты и элементы GPSS/H. Объекты GPSS/H классифицируются по категориям (см. таблицу 3.1), в таблице в графе функции операторов блоков приведены характерные (или единственные) представители операторов рассматриваемой категории.
Таблица 3.1. Объекты GPSS/H
| кат. | Категория объекта | типа | Тип объекта | Мнемонич. обозначение | Функции операторов блоков |
| 1 | Динамическая | 1 | Транзакт | --------- |
Создание транзактов: GENERATE, SPLIT Уничтожение транзактов: TERMINATE, ASSEMBLE |
| 2 | Операционная | 2 | ОБ ( блок ) | ------------ | Объяснены в главе 5 |
| 3 | Аппаратная | 3 | Устройства |
F (facilities) |
Занятие освобождение SEIZE RELEASE Захват возврат PREEMPT RETURN Доступно - не доступно FAVAIL FUNAVAIL Выбор обусловленного направления GATE |
| 4 | Памяти (накопители ) |
S (storages) |
Войти покинуть ENTER LEAVE Свободна занята SAVAIL - SUNAVAIL Ожидание изменения статуса GATE Изменение емкости памяти BSTORAGE |
||
| 5 | Логические ключи |
L (logic switch |
Включение, выключение, инверсия LOGIC Ожидание изменения положения L GATE |
||
| 4 | Вычислительная | 6 | Арифметическая переменная |
V (variable ) |
Целочисленное значение VARIABLE Плавающая точка FVARIABLE |
| 7 |
Булева переменная |
BV | Задается логическими атрибутами СЛА | ||
| 8 | Функция | FN | Задается пользователем или встроенной функцией | ||
| 5 | Статистическая | 9 | Очереди | Q |
Создание очереди покидание QUEUE DEPART |
| 10 | Таблицы | T | Создать таблицу TABULATE | ||
| 6 | Запоминающая | 11 | Ячейки | Х | Создание скалярной переменной |
| 12 | Матрицы | М | Создание 2-х размерных матриц | ||
| 13 | Амперперемен. | Создание переменных 5-ти типов | |||
| 7 | Группирующая | 14 | Списки польз. | С | Включить исключить LINK - UNLINK |
| 15 | Группы | G |
Поместить удалить JOIN REMOVE Проверка принадлежности EXAMINE Определение вида транзакта SCAN Изменение атрибутов - ALTER |
Каждому объекту соответствуют арифметические или логические атрибуты, описывающие состояние объекта в текущий момент модельного времени. Большинство из атрибутов не доступны для программиста.
Атрибуты, к которым в ИМ можно обращаться, называются стандартными числовыми атрибутами (СЧА). Основными объектами GPSS/H являются транзакты и операторы исполнения ОБ (блоки).
Транзакты (сообщения) описывают единицы исследуемых потоков (зHявки на обслуживание), например: задания пользователей в вычислительной системе; детали, подлежащие обработке в ГПС; автомобили в очереди у бензоколонки; корабли, разгружающиеся в порту и т.п.
Операционная категория включает блоки, которые задают логику функционирования ИМ системы и определяют пути движения транзактов между объектами аппаратной категории. Практически все изменения состояний ИМ (события) системы S происходят в результате входа транзактов в блоки и выполнения блоками своих функций.
Основные функции блоков следующие:
создание (генерация) и уничтожение транзактов;
изменение числовых атрибутов объектов;
задержка транзакта на определенный интервал времени;
- изменение маршрута движения транзакта и др.
Проиллюстрируем эти функции на простом примере.
Пример. Блок, создающий транзакты в модели, обеспечивает поступление заявок в СМО через определенные интервалы времени. Занятие или освобождение заявкой канала обслуживания (или места в накопителе) приводит к изменению состояния канала (накопителя). В модели это осуществляется с помощью изменения СЧА объекта GPSS/H, описывающего состояние канала обслуживания (накопителя).
В случае занятости одного из каналов СМО заявка может быть направлена на другой канал. Для этого в модели используется блок изменения маршрута движения транзакта. Блок, осуществляющий задержку транзакта, имитирует процесс обслуживания заявки в течение определенного времени.
Выход обслуженной (или потерянной по каким-либо причинам) заявки из СМО в модели имитируется с помощью блока уничтожения транзактов.
- Объекты аппаратной категории служат для описания единиц оборудования или ресурсов, имеющих ограниченную ёмкость. Воздействуя на эти объекты, транзакты могут изменять их состояния и влиять на движение других транзактов. Ресурсы включают в себя три типа объектов
Устройства описывают оборудование, которое в любой момент времени может быть занято только одним транзактом (одноканальные СМО): обрабатывающий центр, терминал, центральный процессор, АЦПУ, кассир и т.д., а также оборудование, на котором обслуживание одной заявки может быть прервано поступлением другой заявки (например, с более высоким приоритетом).
Памяти (многоканальные устройства) описывают оборудование, которое может использоваться несколькими транзактами одновременно (многоканальные СМО): оперативную память ЭВМ, бункер-накопитель в ГПС, стоянки автомобилей и т.д.).
Логические ключи используются для блокировки или изменения движения транзактов в зависимости от ранее наступивших в ИМ событий.
- Объекты вычислительной категории описывают связи между элементами СС, задаваемые с помощью аналитических или логических соотношений. Они могут служить для задания вероятностных законов распределения случайных величин в ИМ; для численного или логического описания условий, определяющих движение транзактов.
- Статистические объекты обеспечивают вычисление и представление в стандартном виде для показателей эффективности функционирования СС: средних значений, стандартных отношений, эмпирических функций распределения и т.п.
- Запоминающие объекты служат для задания условий моделирования, хранения, накопления и обработки информации, получение которой не предусмотрено стандартными средствами GPSS/H.
- Объекты группирующей категории содержат информацию о транзактах, находящихся в модели. Продвигаясь по модели, транзакты, имитирующие заявки на обслуживание, могут приводить к наступлению таких событий, как: поступление заявки в СМО; занятие (освобождение) места в накопителе; занятие (освобождение) канала обслуживания; прерывание обслуживания заявки с более низким приоритетом; совпадение значений определенных числовых атрибутов двух и более транзактов, называемых синхронизируемыми и т.п. При этом соответствующие транзакты помещаются в один из пяти списков (цепей, в оригинале chain):
-список текущих событий - СТС (время наступления меньше либо равно текущему модельному времени),
-список будущих событий - СБС (время наступления больше текущего модельного времени);
- список прерываний (транзакты, обслуживание которых прервано);
- список синхронизируемых транзактов (находящихся в состоянии сравнения);
- список пользователя содержит транзакты, удаленные программистом из списка текущих событий.
Чтобы при дальнейшем изложении придерживаться единой терминологии введем единое понятия оператора (Таблица 3.2), которое отличается от дословного перевода терминов оригинальной версии языка.
Таблица 3.2 Соответствие английских и русских названий
| Обозначения оригинальной версии языка | Обозначения, введенные в материале |
|
BLOCKS Блоки |
Операторы блоков (блоки) |
|
Сontrol Statements Инструкция управления |
Операторы управления |
|
Compiler Directive Директива компиляции |
Операторы описания |
Длительность испытаний зависит либо от заданной статистической точности, либо от заданного числа реплик в одном прогоне, либо от времени рассмотрения функционирования реальной системы (см. параграф 3.5).
В связи со сказанным необходимо чётко понимать какие времена рассматриваются при ИМ и представлять их различие.
- Тр - реальное время функционирования исследуемой системы S, которое
может быть очень большим, например 10n лет при исследовании космогонических процессов, либо, наоборот, очень малым 10 n секунд при исследовании процессов происходящих в микромире.
- Ти - машинное время имитации, отражающее затраты ресурса времени ЭВМ на организацию ИМ. В случае использования суперкомпьютеров, производительность которых превышает сотни гигафлоп, минута машинного времени может стоить несколько тысяч долларов. Это ограничение должно учитываться создателями ИМ и далее не рассматривается.
- Тм модельное время, используемое в ИМ. Оно может быть сжато при исследовании процессов макромира или растянуто при оперировании со сверхбыстрыми процессами в реальной системе. Кроме того, именно модельное время позволяет избежать сложностей моделирования поведения реальной системы, так в реальной системе события могут происходить одновременно в разных компонентах системы, в обычных не мультипроцессорных ЭВМ параллельные события воплотить нельзя. Модельное время позволяет синхронизовать все события и реализовать квазипараллелизм. При создании ИМ задание временной дискреты модельного времени является обязательным условием до начала процесса ИМ. Естественно, что разные значения времени процессов обязательно должны быть выражены в едином масштабе временной дискреты модельного времени. Так, например, если временная дискрета задана в минутах, другие временные периоды: часы, сутки, годы должны быть так представлены в минутах.
Введем обозначения:
- t0 время начала моделирования (обычно полагают t0 = 0);
- Тм время окончания моделирования;
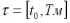
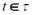
В заключение параграфа приведем ряд определений:
программа или модельный файл - МФ на языке GPSS/H представляет собой описание поведения исследуемой системы, составленное согласно синтаксису языка. Делается это при помощи операторов (таблица 3.2), которые определяют правила перехода системы из одного состояния в другое. Изменение состояния модели называется событием модели.
Одно проигрывание МФ называется реализацией, исполнение всех реализаций, оговоренное параметрами модели (числом стартов или временем моделирования) называется прогоном.
Описание языка моделирования
3.2.1. Структура модели
Модель на языке GPSS/H содержит несколько видов информации, а именно: что происходит с транзактом внутри модели (и с какой вероятностью), в каком режиме должна выполняться модель, сколько должно быть сгенерировано транзактов в этом прогоне модели и т.п., что собой представляют отдельные объекты, встречающиеся в программе. На рисунке 3.1 представлена блок-схема модельного файла.
Модели GPSS/H всегда состоят из нескольких частей, соответствующих этим группам сведений.
Модуль 1 модуль описания и управления. Начинается всегда с ОУ SIMULATE, что дает команду на компиляцию модельного файла.
Модуль также может содержать другие операторы описания и управления. Содержимое модуля задает условия моделирования и само не исполняется.
