Выбор метода построения неманипулируемого механизма
Лемма 11. Максимально возможной заявкой для любого из АЭ для описанной выше обменной схемы является r2 r1.
Доказательство. Из (149) и (150) получаем целевую функцию АЭ1, когда он выступает в роли посредника:fi=(ri-Si/r2)Yi.
А из (149) и (151) - Для АЭ2: f2=(ri r2-S2)Y2.
Очевидно, что для i max st = г^.и
Утверждение 16. При отсутствии возможности кооперации между АЭ и наличии полной информированности АЭ о параметрах ОС, метод доносчика обладает максимально возможной эффективностью
Доказательство. Из леммы 11 следует, что любой из АЭ может стать посредником только в том случае, если сообщит в качестве заявки r2 ri - в, где в - бесконечно малая величина. Из (149) получаем значение функции полезности центра:
(152) fo =( r2 ri - в - c)Yi.
Из (125) и (152), что центр получает прибыль, фактически эквивалентную его прибыли в детерминированной обменной схеме, т.е.K ~ 1. ¦
Следует отметить, что данный механизм обмена также является неманипулируемым - АЭ сообщают истинные значения своих типов.
К сожалению, описанный выше механизм обмена теряет всю свою привлекательность, если АЭ могут кооперироваться между собой, так как элементы будут сообщать минимально возможное значение общего обменного коэффициента - i s = r1 r2. Центр в таком случае получает
максимальный гарантированный результат f0 = (r1 Г2 - c)Y1.
Если же полная информированность АЭ о параметрах обменной схемы отсутствует, или (и) элементы могут кооперироваться между собой, то обменная схема, изображенная на рисунке 15 можно преобразовать в обменную схему, изображенную на рисунке 13.
Результаты, полученные для ОС с двумя АЭ, ниже распространяются
на ОС с конечным числом АЭ.
Рис. 16. Многоэлементная ОС со структурой взаимодействием агентов типа цепочка - конечное число АЭ
Полученные в предыдущих разделах результаты можно перенести на обменные цепочки, состоящие из любого конечного числа АЭ (см рисунок 16). Рассмотрим поочередно каждый из предложенных выше способов.
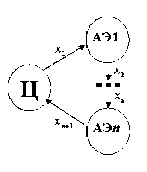
Постановка задачи обмена останется прежней. Обменный коэффициент каждого АЭ имеет для центра интервальную неопределенность -
ri еПі = [Гг,ri].
Способ 1. Результаты леммы 7 можно распространить на случай ограниченного числа АЭ, применив метод индукции - вначале объединяем первый и второй АЭ, затем к вновь образовавшемуся АЭ присоединяем третий АЭ и т.д. Таким образом вновь получается задача обмена между центром и одним АЭ, чью функцию полезности можно записать следующим образом:
fl..n rx1 xn+1,
где
(153) r = П Г, r ?[r, r ], r = П Г, r =П Г -
i=1 i=1 i=1
Также можно записать, что
(154) f = f +УПr,f, -
}=1 i=}+1
Далее задача обмена решается по алгоритму, описанному в способе 1, позволяющему определить множество планов [x1(s),xn+1(s)] , где s=Пsi :
i =1
(155) x,( s) = ^ ^
m( s)
)Y
(156) xn+1( s) = m(r )(s -c(1
m( s)
где
(157) m( s) = [1 + ln c ]-1.
r - c
Для записанного выше механизма обмена очевидным образом доказывается аналог утверждения 12, из чего следует, что данный механизм является механизмом отрытого управления. Т.е. s*=r.
Утверждение 13 также транслируется на случай обменной цепочки из конечного числа элементов - по индукции.
Для построения механизма обмена, в котором также будут фигурировать планы на все трансферты между АЭ (по аналогии с (128),
(129) и (136)), можно в полной мере применить свойства механизма Маскина [66] , так как в обмене у нас участвует ограниченное число АЭ, более трех. Для начала необходимо определить на основании какого дележа будут задаваться трансферты между АЭ.
Лемма 12. Для равного дележа выигрыша коалиции, т.е. когда
Пrrfj =.= Пrif1, необходимо, что бы трансферт ресурса xt для
i=j+1 i=2
i = 2, n задавался выражением
i(n -1)
П rj - (i - 1)П rn
(158) xi =
П'
j =i+1
j=1
j=1
Доказательство. Доказывается данная лемма путем решения системы уравнений, полученных из записанной выше системы равенств и (154). ¦ Также, для равного дележ выигрыша коалиции верна модификация леммы 8 для обменной цепочки с конечным числом АЭ - при таком дележе максимальное значений целевой функции каждого АЭ достигается при s*=r.
Это очевидным образом следует из системы равенств, определяющей дележ и (154).
Теперь мы можем записать механизм открытого управления для цепочки из конечного числа АЭ, построенного на основании механизма Маскина - каждый АЭ сообщает свой вектор s={ ss"}. Затем, если все элементы, за исключением, быть может одного АЭ/ сообщили один и тот же вектор заявок { s, sn*}, то им назначается план (155), (156), (158) где
s = Пs*, ri=s* для i = 1,n. В случае, если заявки АЭ не совпадают, то центр
i=1
выбирает план (155), (156), (158), основанный на некой произвольной комбинации заявок АЭ, например выбирая максимальные оценки обменных коэффициентов:
Гі = si* = max[s/...s"], i = 1,n,
n
s = П s*.
i=1
Способ 2. В модификации способа 2 для обменной цепочки с ограниченным числом АЭ центр последовательно обменивается ресурсами с каждым из АЭ, начиная с первого. Причем полученный от предыдущего АЭ ресурс он передает следующему. Совершенно очевидно, что лемма 9 верна и для данного случая - для обеспечения максимально эффективного обмена центру необходимо целиком передавать АЭі х., полученное от АЭц . Получаем разбиение общей задачи обмена на n подзадач, для каждой из которых можно записать следующую целевую функцию центра:
(159),4 = a,(xi+, - ax),
a
г
,a, ч . і-г
c, a е (^-L,a.+.), i = 1,n -1, a
’ і V ’ i+1 ’ n
a
где a0
1 - обменные коэффициенты центра
i
при обмене с АЭ.
Назначаемый каждому АЭ план можно будет записать следующим образом:
m (r)
Mi(si)
X1
(160) x.
Mr (r)
(s)
ai-1 (1 1
a
m, (r )(s,
)), j = 2, n
m,(s,)
i=1
xn+1 = Y1П m,(r )(si
i=1
a (1 (-
a mi(si) где
(161)m. (s.) = [1 - in aSi - a-1 ]-1.
г г ari -a-1
Утверждение 17. Механизм обмена (160) - является механизмом открытого управления.
Доказательство. Запишем функцию полезности j-ого АЭ,
участвующего в обмене:
/ (?-Sn ) = rjXj (V- Sn ) - Sn ) .
Подставим в трансферты ресурсов, определяемые (160) и (161):
где
(1 ¦ ( 4
a m(si)
W, (s-, Y
(162) f ) = [r
mM,)
(163) x,(s) = П Пm, (r )(s, - a (1
:))¦
¦ .m(s) i=1 ai Mi (si У
X (s )- функция, зависящая только от заявок остальных АЭ
s,= (s1V„,s s ¦¦,sn)¦ Т.е. функцию полезности любого АЭ можно
представить в виде произведения двух функций, одна из которых зависит только от заявки данного АЭ, вторая - только от заявок остальных АЭ: fi(sb...,sn)=fi(si)Xi(s_i).
Легко показать, что максимумf(s) достигается при si*=ri:
f (s) = X/sJm, (r) r~ s ;
os s -a.Ja.
i i i-1 i
r - a , / a
i_i1 i
(s - a_Jai )2
(s)
Xi(s.jMi (ri)
Следовательно, в механизме обмена (160), оптимальной заявкой для каждого АЭ будет истинное значение обменного коэффициента. ¦
Таким образом, нам удалось показать, что механизм обмена (160) является механизмом обмена открытого управления.
В не зависимости от выбранных значений данных параметров, по аналогии с утверждением 15, эффективность механизма (160) будет ниже эффективности механизма (155), (156). Доказывается данное утверждение по индукции.
Способ 3. Отличие в функционировании механизма обмена с разделением ролей для цепочки с ограниченным числом АЭ от цепочки с двумя АЭ заключается лишь в том, что центр выбирает одного бригадира не из двух АЭ, а из всех участников обменной цепочки. Как и в случае с цепочкой из двух АЭ, данный механизм обмена обладает максимально возможной эффективностью (K ~ 1) лишь в случае, когда АЭ полностью информированы о параметрах друг друга и не имеют возможность кооперироваться.
Таблица 3 иллюстрирует принципы выбора метода построения эффективного и неманипулируемого механизма обмена для рассмотренной ОС в зависимости от информированности АЭ и их возможностями по информационно-организационному ИО взаимодействию между собой. Возможность образование коалиции - возможность совместного действия АЭ с целью улучшения общей прибыли АЭ прибыли, в том числе и путем сообщения информации.
Переговоры - возможность передачи информации между АЭ. При этом каждый АЭ преследует собственные цели.
В заключительной главе работы получены следующие результаты. В разделе 3.1 построен эффективный неманипулируемый механизм обмена для многоэлементной ОС с веерным типом взаимодействия агентов.
Исследуемая задача обмена эквивалентна многоэлементной задаче стимулирования в условиях неполной информированности центра.
В разделе 3.2 построены различные неманипулируемые механизмы обмена для многоэлементной ОС с цепочным типом взаимодействия агентов. Определены наиболее эффективные механизмы обмена в
зависимости от возможности информационно-организационного
взаимодействия между АЭ и их информированности.
ЗАКЛЮЧЕНИЕ
В настоящей работе представлена концепция, позволяющая трактовать различные постановки задач управления как задачи обмена. На примере задачи построения неманипулируемых механизмов обмена проиллюстрирована перспективность подобной концепции.
Разработанный общий метод построения неманипулируемых механизмов обмена в активных системах с неполной информированностью центра основан на полученных ранее результатах исследования неманипулируемости механизмов управления, в то время как доказанная эквивалентность задачи обмена и задачи стимулирования позволяет рассматривать построенные в работе неманипулируемые механизмы обмена как механизмы стимулирования.
Основные результаты, полученные в работе, состоят в следующем:
1. Разработана теоретико-игровая модель обменной схемы, в рамках которой обмен определен как процесс перераспределения ресурсов между участниками активной системы. Задача обмена сформулирована как задача управления в активной системе.
2. Разработан общий метод построения неманипулируемых механизмов обмена в активных системах с неполной информированностью центра; получены необходимые и достаточные условия неманипулируе-мости механизмов обмена.
3. Показана эквивалентность задачи обмена и задачи стимулирования в условиях неполной информированности центра, что позволяет использовать результаты исследования задач стимулирования в задачах обмена и наоборот.
4. Построены эффективные неманипулируемые механизмы обмена для:
- двухэлементных иерархических обменных схем с неполной информированностью центра;
- двухэлементной обменной схемы без иерархии в условиях неполной информированности участников
- многоэлементных обменных схем с веерным и цепочным типами взаимодействия агентов.
Перспективными и актуальными представляются следующие направления дальнейшего исследования:
1. Изучение обменных схем со сложными структурами взаимодействия элементов (сетевые структуры).
2. Рассмотрение задач обмена в динамике.
3. Рассмотрение более широкого класса функций полезности участников обменной схемы.
4. Доказательство возможности трактовки большего числа задач управления как задач обмена.
Кроме того, представляется целесообразным расширение области практического применения неманипулируемых механизмов обмена, что, с одной стороны, даст возможность повысить эффективность управления реальными социально-экономическими системами, а, с другой стороны, обогатит теорию новыми постановками задач.
ЛИТЕРАТУРА
1. Ануфриев И.К., Бурков В.Н., Овчинников С.А. Эффективность механизмов обмена в сельскохозяйственной кооперации / Аграрная экономика, политика, история и современность. М. 1996. - 108 с.
2. Ашимов А.А., Бурков В.Н., Джапаров Б.А., Кондратьев В.В. Согласованное управление активными производственными системами. М.: Наука, 1986. - 248 с.
3. Балашов В.Г., Заложнев А.Ю, Новиков Д.А., Задачи назначения центра в линейной активной системе. // Автоматика и Телемеханика 2002 12 с. 92 - 95.
4. Баркалов П.С., Буркова И.В., Глаголев А.В., Колпачев В.Н. Задачи распределения ресурсов в управлении проектами. М.: ИПУ, 2002. -64 с.
5. Багатурова О.С., Кацнельсон М.Б., Красицкая Л.М., Мамиконов А.Г. Управление перераспределением ресурсов путем натурального обмена. М.: ИПУ, 1978. - 80 с.
6. Багатурова О.С., Кацнельсон М.Б., Якубовская Л.Н. Решение задач достройки вариантов обмена неделимых ресурсов / Методы анализа и синтеза автоматизированных систем управления. М.: ИПУ, 1981. -150 с.
7. Бурков В.Н., Багатурова О.С., Иванова С.И., Овчинников С.А., Ануфриев И. К., Маркотенко В. Л. Оптимизация обменных схем в условиях нестабильной экономики. М.: ИПУ, 1996. - 48 с.
8. Бурков В.Н., Данаев Б., Еналеев А.К., Кондратьев В.В., Нанаева Т.Б., Щепкин А.В. Большие системы: моделирование организационных механизмов. М.: Наука, 1989. - 248 с.
9. Бурков В.Н., Зинченко В.Н., Сочнев С.В., Хулап Г.С. Механизмы обмена в экономике переходного периода. М.: ИПУ, 1999. - 72 с.
10. Бурков В.Н., Еналеев А.К. Оптимальность принципа открытого управления.
Автоматика и телемеханика, 1985. 3. C. 73-80.
11. Бурков В.Н., Еналеев А.К., Каленчук В.Ф. Оптимальность принципа открытого управления. Вычислительные процедуры планирования и их свойства // А и Т. 1986.
N 9. С. 81 - 87.
12. Бурков В.Н., Еналиев А.К., Лавров Ю.Г. Синтез оптимальных
механизмов планирования и стимулирования в активных системах. Автоматика и телемеханика, 1992 . 2 10.
С. 113-120.
13. Бурков В.Н., Еналеев А.К., Новиков Д.А. Механизмы
функционирования социально - экономических систем с сообщением информации. Автоматика и телемеханика, 1996 . 3, с. 3-25.
14. Бурков В.Н., Ириков В.А. Модели и методы управления
организационными системами. М.: Наука, 1994. - 270 с.
15. Бурков В.Н., Канцельсон М.Б., Мамиконов А.Г. Прогрессивные механизмы обмена // АиТ. 1983.
1. с. 140-149.
16. Бурков В.Н., Кондратьев В.В. Механизмы функционирования
организационных систем. М.: Наука, 1981.
17. Бурков В.Н., Кондратьев В.В., Цыганов В.В., Черкашин А.М.
Теория активных систем и совершенствование хозяйственного механизма. М.: Наука, 1984. - 272 с.
18. Бурков В.Н., Новиков Д.А.
Введение в теорию активных систем. М.: ИПУ РАН, 1996.
19. Бурков В.Н., Новиков Д.А.
Как управлять проектами. М.: Синтег, 1997. - 188 с.
20. Бурков В.Н., Новиков Д.А.
Модели и механизмы теории активных систем в управлении качеством подготовки специалистов. М.: ИЦ, 1997. - 158 с.
21. Бурков В.Н., Новиков Д.А.
Теория активных систем: состояние и перспективы. М.: СИНТЕГ, 1999. - 128 с.
22. Бурков В.Н., Новиков Д.А.
Управление организационными системами: механизмы, модели, методы // Приборы и системы управления. 1997.
N 4. С. 55 - 57.
23. Гермейер Ю.Б.
Игры с непротивоположными интересами. М.: Наука, 1976. - 328 с.
24. Гуриев С.М., Икес Б.У.
Бартер в России. М.: Российская экономическая школа, 2000. - 19 с.
25. Заруба В.Я.
Аналитическое проектирование мотивационных процедур планирования. Х: Бизнес Информ, 1998. - 248 с.
26. Зинченко В. И. Модели и методы оптимизации обменных схем. М.: ИПУ, 2001 - 25 с.
27. Данилов В.И., Сотсков А.И.
Механизмы группового выбора. М.: Наука, 1991.
28. Интрилигатор М. Математические методы оптимизации и
экономическая теория. М.: Прогресс, 1975. - 606 с.
29. Каленчук В.Ф.
Разработка и исследование оптимальных процедур планирования в активных системах в условиях неопределенности. М.: ИПУ РАН, 1990. - 22 с.
30. Клейнер Г.Б. Производственные функции: теория, методы,
применение. М.: Финансы и статистика, 1986. - 238 с.
31. Кацнельсон М.Б.
Перераспределение ресурсов. М.: Наука, 1985.
32. Караваев А.П., Коргин Н.А. Оптимальные унифицированные системы стимулирования в задаче управления активными системами./ Материалы международной научной конференции "Современные сложные системы управления".
Старый Оскол: СТИ, 2002. С. 134-137.
33. Коргин Н.А. Механизмы открытого управления в обменных схемах / Труды юбилейной международной научно-практической конференции "Теория активных систем". М.: Синтег, 1999.
С. 118.
34. Коргин Н.А. Механизмы открытого управления в двухэлементных обменных схемах / Сборник трудов молодых ученых ИПУ РАН.
М.: Фонд "Проблемы управления", 2000. С. 54 - 58.
35. Коргин Н.А. Механизмы открытого управления в многоэлементных обменных схемах/ Труды международной научно-практической конференции "Управление большими системами".
Тбилиси: ТГУ, 2000. С. 24 26.
36. Коргин Н.А. Механизмы открытого управления в симметричных
обменных схемах/ Тезисы докладов XLIII научной конференции МФТИ "Современные проблемы фундаментальных наук".
Долгопрудный: МФТИ, 2000. С. 34.
37. Коргин Н.А. Задачи теории активных схем с точки зрения обменных схем / Труды международной научно-практической конференции "Теория активных систем".
М.: ИПУ РАН, 2001. Т. 1. С. 45.
38. Коргин Н.А.
Эффективность применения механизмов открытого управления в многоэтапных обменных схемах / Труды международной конференции "Современные сложные системы управления предприятием". Липецк: ЛГТУ, 2001.
С. 113 - 116.
39. Коргин Н.А. Задача стимулирования и обменные схемы // Автоматика и Телемеханика. 2001. 10.
С. 147 - 153.
40. Коргин Н.А. Механизмы открытого управления как способ
повышения надежности функционирования сложных систем / Труды IX Международной конференции "Проблемы управления
безопасностью сложных систем". М.: ИПУ РАН, 2001.
С. 98.
41. Коргин Н.А.
Информация как обмениваемый ресурс./ Тезисы докладов XLII научной конференции МФТИ "Современные проблемы фундаментальных наук". Долгопрудный: МФТИ, 2001.
С. 25.
42. Коргин Н.А.
Механизмы открытого управления в многоэлементных обменных схемах с одним АЭ на каждом уровне./ Труды пятой ежегодной научной конференции "Сократовские чтения 2002". Москва: "Международный университет", 2002.
С. 51.
43. Коргин Н.А. Общий метод построения механизмов открытого управления для обменных схем / Сборник трудов молодых ученых "Управление большими системами". М.: ИПУ РАН, 2003.
Выпуск 3. С. 48 - -55.
44. Макаров И.И.
Бартер и корпоративное управление в России. М.: Российская экономическая школа 2000 - 37 с.
45. Новиков Д.А.
Механизмы стимулирования в динамических и многоэлементных социально-экономических системах // А и Т. 1997. N 6. С. 3 - 26. 5
46. Новиков Д.А.
Оптимальность правильных механизмов управления активными системами. I. механизмы планирования, II. Механизмы стимулирования.
Автоматика и телемеханика, 1997, 2-3.
47. Новиков Д.А.
Оптимальность правильных механизмов управления активными системами. II.
Механизмы стимулирования // А и Т. 1997. N 3. С. 161 - 167.
48. Новиков Д.А.
Стимулирование в социально-экономических системах / Базовые математические модели. М.: ИПУ, 1998. - 216 с.
49. Новиков Д. А. Механизмы стимулирования в динамических и многоэлементных социально-экономических системах // Автоматика и Телемеханика. 1997.
6. С. 3 - 26.
50. Новиков Д.А.
Сетевые структуры и организационные системы. М.: ИПУ РАН, 2003. - 102 с.
51. Новиков Д.А. Обобщенные решения задач стимулирования в активных системах.
М.: ИПУ РАН, 1998.
52. Новиков Д.А., Петраков С.Н.
Курс теории активных систем. М.: СИНТЕГ, 1999. - 108 с.
53. Петраков С.Н.
Механизмы планирования в активных системах: неманипулируемость и множества диктаторства. М.: ИПУ РАН, 2002. -135 с.
54. Суворов А.Д.
Бартер и долгосрочные отношения. М.: Российская экономическая школа, 1999 - 32 с.
55. Теория активных систем / Труды Юбилейной международной научнопрактической конференции. М.: СИНТЕГ, 1999. - 320 с.
56. Фишберн П. Теория полезности для принятия решений. М.: Наука, 1978. - 352 с.
57. Фокин С.Н.
Разработка, исследование и применение процедур распределения моноресурса в социально-экономических системах в условиях неопределенности с учетом приоритетов потребителей (на примере распределения машинного времени на ВЦ в отраслевых НИИ и КБ) / Диссертация на соискание ученой степени канд. техн. наук. М: ИПУ РАН, 1988. - 166 с.
58. Цыганов В.В.
Адаптивные механизмы в отраслевом управлении. М.: Наука, 1991. - 166 с.
59. Akerlof G. The Market for "Lemons": Qualitative Uncertainty and the Market Mechanism // Quarterly Journal of Economics.
1970. vol. 89. p. 488-500
60. Arrow K.J.
Social choice and individual values. Chicago: Univ. of Chicago, 1951. - 204 p.
61. Arrow K.J., Radner R. Allocation of resources in large teams // Econometrica. 1979.
Vol. 47.
N 2. P.361 - 386.
62. Burkov V.N., Lerner A.Ya. Fairplay in control of active systems / Differential games and related topics.
Amsterdam, London: North-Holland publishing company, 1971. P. 325 - 344.
63. Burkov V.N., Novikov D.A., Petrakov S.N.
Mechanism design in economies with private goods:trthtelling and feasible message sets. XIII Conference on system science, 1998. Vol.3 P.255-262
64. Cramton P. C. Bargaining with Incomplete Information; An Infinite-Horizon Model with Two-Sided Uncertainty // Review of Economic Studies.
1984. vol. 51. p. 579-593
65. Craword V., Sobel J. Strategic information transmission // Econometrica.
1982. vol 50 pp. 1431-1451
66. Dasgupta P., Hammond P., Maskin E. The implementation of social choice rules: some general results on incentive compatibility.
Review of Economic Studies, 1979, The Symposium on Incentive Compatibility.
67. Fudenberg D., Levine D., Tirole J. Infinite-horizon models of bargaining with one-sided incomplete information / Game Theoretic Models of Bargainig. Cambridge University press, 1985. p. 73-98
68. Fudenberg D., Tirole J. Sequental Bargaining with Incomplete Information // Review of Economic Studies. vol.
50. 1983. p. 221-247
69. Gjesdal F. Information and incentives: the agency information problem // Review of Economic Studies. 1982. Vol. 49.
N 2. P. 373 - 390.
70. Green J., Laffont J.-J.
Partially verifiable information and mechanism design // Review of Economic Studies. 1986. Vol.
53. N 4. P. 447 - 456.
71. Guriev S., Kvasov D. Barter in Russia: Role of market power. M.: RECEP 1999 - 22 p.
72. Hammond P.J.
Straightforward individual incentive compatibility in large economics // Review of Economic Studies. 1979.
Vol. 46.
N 2. P. 263 - 282.
73. Harris M., Raviv A. A. Theory of Monopoly Pricing Schemes with Demand Uncertainty // The American Economic Review. vol.
71. N. 3. 1981. p. 347-365
74. Harris M., Townsend R. Resource Allocation under Asymmetric Information // Econometrica. vol.
49. 1981. p. 33-64
75. Hurwicz L. On informationally decentralized systems // Decision and organization.
Amsterdam: North-Holland Press, 1972. P. 297 - 336.
76. Kim S.K.
Efficiency of an information system in an agency model // Econometrica. 1995.
Vol. 63.
N 1. P. 89 - 101.
77. Kreps D., Wilson R. Reputation and Imperfect Information // Journal of Economic Theory. vol.
31. 1982. p. 251-268
78. Laffont J.-J., Maskin E. Nash and dominant strategy implementation in economic environment // J. of Mathematical Economy.
1982. Vol.
10. N 1. P. 17 - 47.
79. Martimort D., Stole L. The Revelation and Delegation Principles in Common Agency Games.// Econometrica 2001. pp 350-380.
80. Mas-Collel A., Vives X., Implementation in economies with a continuum of agents // Review of Economic Studies. 1993.
Vol. 60.
N 3. P. 613 - 629.
81. Mas-Colell A., Whinston M.D., Green J.R.
Microeconomic theory. New-York: Oxford University Press, 1995. - 1000 p.
82. Maskin E., Tirole J., The Principal-Agent relationship with informed principal. // Econometrica, 1992. vol 60. pp 1-42.
83. McCelvey R. D. Game Forms for Nash Implementation of General Social Choice Correspondences. Social Choice and Welfare, 1989.
6. P. 139156.
84. Moore J. Implementation, contracts and renegotiation in environment with complete information / Advances in Economic Theory. Cambridge: Cambridge University Press, 1992. Vol.
1. P. 182 - 281.
85. Myerson R.B.
Game Theory / Analysis of Conflict. Harvard University press, 1991. - p. 568
86. Myerson R.B.
Incentive Compatability and The Bargain Problem // Econometrica. vol. 47. 1979. p. 61-74
87. Myerson R. Optimal coordination mechanisms in generalized principal -agent problems // J. of Mathematical Economy. 1982. Vol. 10.
N 1. P. 67 - 81.
88. Repullo R. The Revelation principle under complete and incomplete information. Economic Organizations as Games.
Oxford: Basil Blackwell,1986. P. 179 - 195.
89. Rubenstein A. A bargaining model with incomplete information // Econometrica. vol.
53. 1985. p. 1151-1172
90. Saijo T. Strategy space reduction in Maskin's Theorem: sufficient conditions for Nash implementation. Econometrica, 56.
P. 693-700.
91. Salanic B. The Economies of Contracts.
1997. 507 p.
92. Sen A. Collective choice and social welfare. London: Holden - Day, 1970. -254 p.
93. Sen A. Social choice theory / Handbook on mathematical economics.
Vol. 3. Amsterdam: North-Holland, 1986.
P. 1073-1181.
94. Shubik M. Game theory in the social sciences: concepts and solutions.
Massachusetts: MIT Press, 1991.
95. Tirole J. The theory of industrial organisation. The MIT Press, 1997. -502 p.
