ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ НЕМАНИПУЛИРУЕМЫХ МЕХАНИЗМОВ ОБМЕНА В АКТИВНЫХ СИСТЕМАХ
В данной главе формулируется математическая модель ОС, ставится задача обмена. Проводится сравнительный анализ оснований для классификации АС и ОС, в результате которого обосновывается актуальность рассмотрения задач ТАС как задач обмена. Приводится обзор основных известных моделей и методов, которые могут быть использованы для построения неманипулируемых механизмов обмена для ОС. Формулируется общая постановка задачи построения неманипулируемых механизмов обмена для АС с неполной информированностью центра.
Предложен общий метод решения этой задачи. Выводятся необходимые и достаточные условия неманипулируемости механизма обмена, сформулированные в терминах функций предпочтения агентов.
Полученные автором результаты, содержащиеся в первой главе, были опубликованы в работах [33,37,40,43].
1.1. Модель обменной схемы
Понятие обмена можно понимать в буквальном смысле - считая обменными бартерные схемы. Можно попытаться расширить рамки понятия процесса обмена, рассматривая его, как процесс взаимодействия между членами социально-экономической системы с целью улучшения своего благосостояния.
Для этого необходимо построить модель обменной схемы, которая не противоречит проводимым ранее исследованиям бартерных схем [1,5,6,7,9,15,24,26,31,44] и позволяет рассмотреть другие задачи функционирования социально-экономической системы (активной системы в терминах ТАС) как задачи обмена.
Рассмотрим АС, состоящую из n+1 агентов и т видов ресурсов. Множество всех агентов обозначим I = {0,...,n}.
Множество всех ресурсов обозначим J = {1,...,m}. Набор всех имеющихся у агента i ресурсов обозначим yi = (,...,угт).
Здесь yj обозначает наличие у i-ого агента ресурса типа j. Соответственно распределение ресурсов по всем агентам можно записать в виде матрицы: у = (y0,.., yn)T.
Нумерация агентов от 0 до n оправдана тем, что большинство ОС, рассматриваемых в данной работе будут представлять из себя АС, состоящие из одного руководящего агента и n подчиненных ему агентов. Функции и возможности руководящего и подчиненных агентов будут рассмотрены ниже, при описании структуры подчиненности агентов.
Предпочтения каждого агента опишем произвольной функцией (функция предпочтения): j (у1): Rm ® R; i = 0,n +1.
Агенты обладают возможностью взаимодействовать между собой путем взаимного обмена ресурсами.
Определение 1. Обмен - перераспределение ресурсов из множества Jмежду элементами из множества I: у ^у .
Здесь у0 - матрица начального распределения ресурса (или существующего распределения), уе - соответственно конечного.
Определение 1 и само описание набора агентов и ресурсов выглядят пока достаточно абстрактно, но именно данный подход позволяет дать наиболее общее определение обменной схемы и самого процесса обмена. Рассмотрим качественно, какие ограничения (требования) могут быть наложены на описанную выше модель и приведем примеры данных ограничений.
Данные ограничения могут трактоваться как основания для классификации ОС.
Ограничения по ресурсам. Ограничения данного класса определяют множества всевозможных значений матрицы распределения ресурсов у: уеA.
Примером подобных ограничений являются ограничения на общееколичество ресурса ^ у1. = Y , и ограничения на количество ресурсаi=o(ресурсов) у отдельного агента, например уг} Yj.
Ограничения по возможности взаимодействия между агентами.
Ограничения данного класса фактически превращают некий произвольный набор агентов в сетевую структуру - указывают, с какими агентами данный конкретный агент может обмениваться какими ресурсами. На рисунке 1 приведен пример ограничений данного класса -линии, связывающие агенты указывают на возможность взаимодействия (обмена) между ними, подписи к линиям - указывают на типы ресурсов, которыми данные агенты могут обмениваться. Ограничения данного класса обозначим QS.
Запись y^ye е Qs обозначает, что обмен /-/ возможен в рамках определенной структуры.
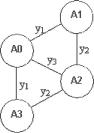
Рис. 1. Структура взаимодействия агентов
Ограничения на вид функций предпочтения агентов. Этодостаточно широкий класс ограничений.
Например, функции всех агентов принадлежат к классу вогнутых однопиковых непрерывных функций. Или вид функций предпочтения может быть указан явным образом, например:
m i
j =z Bi(yi -a) Pi.
i=i
Ограничения данного класса обозначим Q9.
Ограничения индивидуальной рациональности IR(p).
Ограничения данного класса определяют требования, налагаемые на
значения функций предпочтения агентов. Например i е I j(уег) j(y).
Множество распределений ресурсов, индивидуально рациональных по отношению к начальному распределению ресурса, обозначим IR(y). Очевидно, что IR(y) с A.
Накладывая на рассматриваемую схему ограничения приведенных выше четырех классов в различных комбинациях, можно получить достаточно большое количество моделей взаимодействия агентов.
Пример 1. Схема "Распределение ресурсов" (см. рисунок 2)
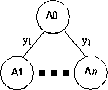
Рис. 2. ОС Распределение ресурсов
Опишем модель АС, используемую в задаче распределения ресурсов [4,16,18,25,29,52,57] в терминах обменных схем:
1. Кол-во агентов - n+1 (Центр - агент с номером 0)
2. Кол-во видов ресурсов - 1
3. Ограничения на ресурс A: ^y = Y1i=o
4. Ограничения QS: агенты с номерами i = 1, n могут взаимодействовать только с агентом номер 0 (центр).
5. Ограничения Q9: функции благосостояния для агентов с номерами i = 1, n - однопиковые, максимум функции благосостояния k-ого достигается при наличии у него ресурса в кол-ве rk.
6. Ограничения ИР зависят от начального распределения ресурса и записываются следующим образом = П У е Л j (yt) ^ j (y-0)
7. Начальное распределение ресурса: у0 = (Yn0,...,0)T
Рассмотренная схема позволяет трактовать задачи распределения ресурсов [4,16,18,25,29,52,57] как задачи обмена?
После введения четырех классов ограничений можно записать ряд ключевых определений.
Определение 2. Множество возможных вариантов обмена (МВО) У(У): Y(y0) е IR(A y е Y(y0), y^y е Qs .
Т.е множество возможных вариантов обмена - совокупность всех индивидуально рациональных распределений ресурсов, переход к которым от начального распределения ресурсов возможен в рамках заданной структуры.
Определение 3. Обменная схема (ОС) - кортеж {I, J, A, y0, Qs, Qq,, IR(y0)}, для которой МВО не пусто.
Для обменных схем можно вести следующие замены:
Определение 4. Трансферт ресурса типа j для элемента i в процессе обмена y^y : xj = yj - yj0.
Соответственно можно определить xi = (-1,..., Xm) - вектор трансфертов всех ресурсов у элемента i; матрица трансфертов в ОС -x =(-V-X) T.
Данная замена актуальна тем, что любой из возможных обменов в ОС однозначно определяется матрицей х. В то время как различным вариантам обмена может соответствовать одинаковое конечное распределение ресурса между агентами.
Определение 5. Множество возможных вариантов обмена в терминах трансфертов Х: хеX $y е Y(y0) : х = y -y.
Множество Х зависит от y0, но, учитывая, что в определении обменной схемы мы рассматриваем единственное начальное распределение ресурсов, аргумент y0 опускается.
Определение 6. Функция полезности i-го агента от обмена:/г (Хг ) = j (Хг + Уі ) - j (Уі ).
По аналогии с множеством Х, аргумент у в записи функции полезности опускается. Очевидно, что свойства функции полезности абсолютно идентичны свойствам функции предпочтения.
Фактически, функции полезности от обмена - это и есть функции предпочтения, но рассматриваемые в новой системе координат (трансфертах), полученной путем сдвига из стартовой системы координат (ресурсы).
Пример 2. Пусть предпочтения агента описываются функцией j(у1,у2) = у2 - (у1 - У1)2. Тогда, в соответствии с определением 6, множество Х зависит от у0, но, учитывая, что в определении обменной схемы мы рассматриваем единственное начальное распределение ресурсов, аргумент у0 опускается.
Таким образом, целевая функция в обменной схеме для данного агента будет иметь следующий вид:
f (Xl, x2 ) = Х2 - Х12 + 2Xj (Уі - Y).
При начальном наборе ресурсов у данного агента {Y^O}, его целевая функция переписывается следующим образом
f (Xj , x2) = Х2 - Х12.^
Также, важными понятиями в рассмотрении обменных схем, являются понятие структуры подчиненности и понятие информационного состояния схемы.
Структура подчиненности определяет иерархию в обменных схемах -т.е. кто определяет правила и последовательность обмена и предлагает возможные варианты обмена для всей схемы. Отметим, что структура подчиненности может не иметь ничего общего со структурой схемы, определяемой ограничениями QS. Одним экстремумом множества возможных структур подчиненности является равноправная структура -когда все агенты оказывают сравнимое влияние на выбор вариант обмена или правила обмена.
В противоположность данной структуре можно поставить иерархическую структуру с двумя уровнями иерархии - из множества всех агентов выделяется один, в подчинение которого находятся все остальные агенты схемы. Используя терминологию ТАС [52], главенствующего агента можно назвать центром (Ц), находящихся у него в подчинении агентов - активными элементами (АЭ).
Для рассмотрения более сложных структур подчиненности можно для /-ого агента ОС ввести следующую характеристику - (lf;lf). if - множество агентов ОС, которым данный агент подчиняется непосредственно. if -множество агентов ОС, находящихся в непосредственном подчинении у данного агента.
Информационное состояние ОС определяет информированность агентов о параметрах ОС. В данной работе сохраняется классификация, принятая в [14,18,19,52]. В соответствии с данной классификацией, основное внимание в данной работе уделяется ОС с неполной и ассиметричной информированностью агентов. Агент считается не полностью информированными, если ему не известны точные значения всех параметры ОС.
Информационное состояние системы считается ассиметричным, если агенты обладают разными уровнями информированности о параметрах ОС.
Введя базовые определения, необходимые для рассмотрения обменных схем, перейдем к формулировке задачи обмена.
1.2. Общая постановка задачи обмена в активной системе
Самая общая постановка задачи обмена может быть сформулирована как стандартная задача управления [18,52]. Реализация любого из вариантов обмена зависит от управляющего воздействия u е U: x =G(u).
Пусть на множестве U*X задан функционал Ф(и, x), определяющий эффективность обмена с точки зрения управляющего органа (например центра самого верхнего уровня, или совокупности всех элементов для равноправной ОС). Величина K(u) = Ф(и, G(u)) называетсяэффективностью управления u е U. Задача управляющего органа заключается в выборе максимально эффективного допустимого управления:
u * е Argmax K(u) = { u е U | V v е UK(u) K(v)}.
ueU
1.3. Рассмотрение задач теории активных систем как задач обмена
Прежде чем обосновать смысл рассмотрения задач ТАС как задач обмена, произведем сравнительный анализ классификации ТАС и классификации ОС, предложенной в данной работе.
Базовая модель АС задается следующим набором параметров [16, 52], который также служит основанием для классификации задач ТАС.
Состав АС - совокупность субьектов, являющихся агентами системы (участниками АС).
Структура АС - совокупность информационных, управляющих и других связей между участниками АС, включая отношения подчиненности и распределения прав принятия решений.
Порядок функционирования - последовательность получения информации и выбора стратегий участниками АС.
Число периодов функционирования - отражает наличие или отсутствие динамики в рассматриваемой АС.
Предпочтения участников АС - определяют совместно с принципами рационального поведения зависимость состояния системы от управляющих воздействий и критерий эффективности системы.
Допустимые множества состояний (стратегий) участников АС -отражают индивидуальные и общие ограничения на выбор состояний, накладываемые окружающей средой, используемой технологией и т.д.
Информированность участников - та информация, которой обладают участники.
Из данного набора параметров часть сохранена и в описании модели обменной схемы. Это состав системы, порядок функционирования, число периодов функционирования и информированность участников, которая в данной работе формулируется как структура информированности агентов ОС.
Затемненные области в приведенной выше таблице указывают на пересечение критериев классификации модели АС и ОС по смыслу. Поясним эти пересечения.
Структура системы распадается на два параметра - структура подчиненности, и структуру взаимодействия, задаваемую ограничениями на возможность взаимодействия между агентами. Причем последний параметр больше принадлежит к группе допустимые множества из классификации ТАС, так как является именно ограничением в модели.
Разделение параметра предпочтения участников системы - всего лишь углубление классификации, позволяющее более четко прояснить структуры модели ОС. Параметр допустимые множества преобразуется прежде всего ограничения на ресурс, но возможность обмена агентов между собой в соответствии с некой структурой также можно расценивать как ограничения на выбор состояний участниками АС.
Таким образом, ОС - это АС, при исследовании которых акцент делается на возможности взаимодействия агентов между собой (обмена ресурсами).
Совершенно очевидно, что многие (если не все) задачи ТАС, могут быть рассмотрены как задачи обмена.
Задачи стимулирования [2,8,12-14,16-22,45-52,55,58] - центрвзаимодействует с активными элементами, требуя от них каких то
действий и назначая стимулирование за эти действия. Взаимодействие между центром и АЭ может быть представлено в виде обмена - центр обменивает свой ресурс (например деньги) на ресурс АЭ - их работу, товар, т.д.
Поэтому очевидно, что задачи стимулирования могут рассматриваться как задачи обмена. В разделе 2.1 приводится строгое доказательство эквивалентности задач стимулирования и обмена.
Задачи распределения ресурса [4,16,18,25,29,52,57] - центр неким образом распределяет имеющийся у себя в наличии ресурс между АЭ. В примере 1 рассмотрена ОС, где возможен только односторонний обмен - один агент может распределить имеющийся у него в наличии ресурс между остальными. Иными словами задачи распределения ресурсов можно представить как частный случай задач обмена.
Представляется перспективным перенос результатов ТАС, полученных для задач распределения ресурсов.
Задачи определения внутренних цен [2,7,13,14,16,17,19-22,25,26,55,58] также могут быть рассмотрены как задачи обмена, где ресурсами к обмену являются деньги и товары.
На рисунке 3 представлена структура рассматриваемых в работе обменных схем. В главе 2 будут рассмотрены двухэлементные ОС, для которых задачи обмена могут быть классифицированы как эквивалентные задачам стимулирования, эквивалентные обратным задачам стимулирования (центр стал АЭ, а АЭ - центром) и как классический обмен - функции предпочтения агентов линейно зависят от количества имеющихся у агентов ресурсов.
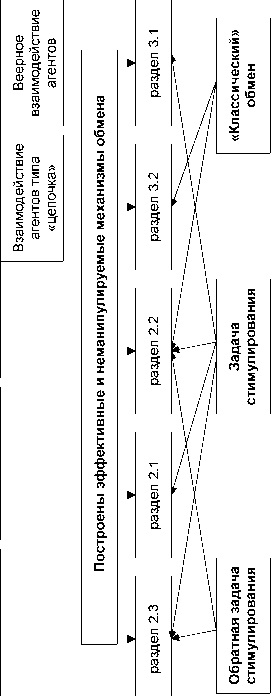
Рис. 3. Рассматриваемые обменные схемы
1.4. Математические модели и методы, используемые для построения неманипулируемых механизмов обмена в активных системах
В данном разделе приведем основные результаты ТАС и микроэкономической теории, применимые для построения неманипулируемых механизмов обмена в активных системах
Условия совершенного согласования. В отечественных работах авторы сосредоточили внимание на способах организации деятельности отдельных элементов системы. В [10-14,16-22,52,53,55,58,62,63] исследуются механизмы функционирования систем, в которых альтернатива представляет собой вектор Евклидова пространства, причем в функции полезности каждого активного элемента явно участвует только одна компонента этого вектора, обычно содержательно интерпретируемая как план, назначаемый данному элементу.
Такие системы в зарубежных работах получили название экономик с частными товарами (Economies with private goods) [45,61,72,53,55,].
Рассмотрим систему, состоящую из центра и n активных элементов. Интересы элементов и центра выражаются их целевыми функциями
fi (xi, yi, ri), i = 1, n и Ф(x, y) где ri e Wi - параметр, параметризующий класс допустимых целевых функций i - го элемента, x = (x^ ..., xn) - вектор планов, назначаемых элементам, а у = (уь ..., yn) - вектор действий, выбираемых элементами. Порядок функционирования системы следующий:
1. Этап сбора информации. Элементы сообщают центру оценки (sb ..., sn) параметров (гь ..., rn);
2. Этап планирования. На основе полученных оценок центр, используя процедуру планирования p : S ® X, где S = nj, X = п хі -ieI ieIмножество допустимых планов, назначает планы xi = pi (s) элементам, i = 1, n.
3. Этап выбора состояния. Получив плановые задания, элементы выбирают свои состояния yi eAi, где A, i = 1, n - множества допустимых состояний.
В предположении рационального поведения элементов, при фиксированных планах выбираемые действия у* будут максимизировать соответствующие целевые функции, то есть:
У* е Pi (xi, ri) = Argmax f (Xj, yj, r).
y^Ai
Как и ранее, при сообщении оценок на этапе 2, будет иметь место эффект манипулирования информацией. Задачей центра является выбор такой процедуры планирования, чтобы в точке равновесия значение его целевой функции было максимально. Введем эффективность механизма S = (S, p)
K(S) = min Y(p(s*), r),
reS
где Y(x, r) = F(x, у * (x, r)).
При заданных значениях параметра ri eW i и плане xi e Xi элементвыбирает действие у* (xi, ri) e Pi (xi, ri) = Argmax fi (xi, yi, ri). ТакимyieAiобразом, можно говорить о функции предпочтения (полезности) элемента
ji(xi, ri) = fi(xi, y*(xi, ri X ri).
Зададим для каждого активного элемента множества Хг(s_г) с Хг и рассмотрим следующую процедуру планирования:
xeX
(5.1) fY (x, s) ® imx
j(X, S) = 1^!ax)j(Z S).
zeXi (s_i)(5.2)
Условие (5.2) обеспечивает назначение элементу плана, максимизирующего его функцию предпочтения (в которую в качестве истинного значения типа АЭ подставляется сообщенная им оценка) и называется условием совершенного согласования (УСС). Условие (5.1) в неявном виде задает процедуру планирования, максимизирующуюцелевую функцию центра.
Механизм, удовлетворяющий (5.1)-(5.2), называется механизмом открытого управления (ОУ).
Теорема 5.1.2 [52] (Принцип открытого управления). Необходимым и достаточным условием сообщения достоверной информации как доминантной стратегии при любых r е W является существование множеств X.(s _г), для которых выполнено условие совершенного согласования. ¦
Таким образом, принцип открытого управления является критерием неманипулируемости механизма планирования в АС с сообщением информации. Помимо манипулируемости, основным свойством любого механизма является его эффективность.
Возникает вопрос, в каких случаях существует оптимальный неманипулируемый механизм (другими словами - в каких АС при поиске оптимального механизма можно ограничиться классом неманипулируемых механизмов). Частичный ответ на этот вопрос дает теорема 5.2.
Теорема 5.2. [52] В активной системе с одним активным элементом для любого механизма планирования существует механизм открытого управления не меньшей эффективности. ¦
Итак, теорема 5.2 утверждает, что механизм ОУ оптимален в одноэлементной АС (другими словами, для любого механизма планирования в одноэлементной активной системе существует эквивалентный прямой механизм. Естественное желание обобщить этот результат на случай многоэлементных АС наталкивается на ряд проблем, основная из которых - зависимость равновесного сообщения s*(r) каждого АЭ i е I от типов других АЭ [13].
Поэтому в общем случае в многоэлементных АС механизмы открытого управления (неманипулируемые) не оптимальны. В то же время, для широкого класса практически важных частных случаев механизмов планирования в многоэлементных АС доказаны результаты об оптимальности механизмов ОУ. Некоторые из этих механизмов рассматриваются в работах
2 В разделе 1.4 нумерация определений, лемм, теорем, формул и т.д. соответствует их нумерации вв источниках. 22
[8,13,19,48,52,55]. В данной работе УСС будут использованы в общем методе построения неманипулируемых механизмов обмена, а теорема 5.2 обосновывает оптимальность неманипулируемых механизмов обмена, которые будут построены в главе 1.
Оптимальность неманипулируемых механизмов распределения ресурсов [4,13,14,16-22,46,47,52,53,55,63]. Рассмотрим систему, состоящую из центра и n активных элементов.
Центр владеет R0 единицами ресурса. Ценность ресурса для i -го элемента определяется его функцией полезности j (xi, r), где xi - получаемое им количество ресурса, а г. - тип АЭ, параметризующий класс допустимых функций полезности. Функция полезности может определять, например, прибыль АЭ от использования ресурса в количестве xi .
Предположим, что о функции полезности АЭ центр не имеет информации, за исключением той, что она принадлежит некоторому классу однопиковых функций с точкой пика r eQ. и однозначно определяется значением этого параметра, то есть получение ресурса в количестве x. = r доставляет максимум функции полезности i-го АЭ.
Задачей центра является распределение ресурса с целью, например,максимизации суммарной полезности всех элементов ^ (р. (хг, г) ® maxieI х"
при ресурсном (балансовом, бюджетном) ограничении: ^ хг R0.
Распределение ресурса осуществляется следующим образом. Каждый активный элемент сообщает центру оценку у eQ i, i e I, своего типа
(параметра своей функции полезности) рг (xt, r) и получает ресурс в количестве xt = p (s), где p(s) = (p(s), p2(s),..., nn (s)) называется процедурой (механизмом) распределения ресурса.
Будем полагать, что множество возможных значений типов i-го АЭ Q.
- является отрезком действительной оси: Q. = [0, D] с R\ i e I, 0 D +?. В качестве ограничения D можно выбрать, например, имеющееся в распоряжении центра количество ресурса R0.
На процедуру распределения ресурса наложим следующие ограничения:
1. Функция p (я) непрерывна по всем переменным и строго монотонна по у. для всех я е [0, D]п, і е I.
2. Будем считать, что ^ r R0 (гипотеза дефицитности) и весь ресурсраспределяется полностью, то есть: ^ х = R0.
3. Каждая группа активных элементов может получить любое количество ресурса, меньшее того, что она уже получила:
у е W, W с I x p (у), і е W 3 sw eW ж : xw = nw (sw, w),
где Ww = nW j-Іе-W
4. Если количество ресурса, распределяемого между АЭ из некоторого подмножества W с I, увеличивается, то каждый АЭ получает количество ресурса, не меньшее прежнего.
В качестве модели поведения примем равновесие Нэша. Вектор сообщений у * (г) называется равновесием Нэша при данном r еО, если і е I, уг е Wг выполняется следующее соотношение:
j (pi (у * ), Гг ) j (pi (Уі , у-г ), Г ).
Лемма 5.1. [52] Пусть у * (г) - равновесие Нэша при данном r, тогда оно удовлетворяет следующим условиям:
1) если х* r, то у * = D;
2) если у * е [0, D), то x* = r .¦
Распределение ресурса в равновесии определяется следующим алгоритмом.
Алгоритм 5.1. [52] На нулевом шаге полагаем уг0 = D для всех і е I и вычисляем распределение ресурса x = p(D, ..., D). Множество Q на нулевом шаге полагаем пустым Q0 = 0.
На шаге j 1 множество Q1 определяем следующим образом:Q1 = {і Е11 (x1-1) i r }.
Для АЭ из множества Q1 по условию 2 определяем sQj е W Qj такие, чтоp , (s ., sJ-1.) = r . .QjK Qj ’ I\QJ J QJ
В конце j -го шага получим s1 = (sqJ , sJQJ) и x1 = p(S).
Если на некотором шаге k окажется, что Qk = Qk-1, то алгоритм останавливается, и полагаем: s* = sk, x* = xk, Q = Qk. -
Результаты применения данного алгоритма, заканчивающегося не более чем за n шагов, имеют следующие свойства:
Лемма 5.2. [52] 1) Если і € Qk, то на любом шаге 1 j k, x1 x1 -1 и x x .
2) s* - равновесие Нэша при данном r. ¦
Определим соответствующий исходному механизму распределения ресурса прямой механизм h(r) = p(s * (~)), ~ eW . Таким образом, в механизме h(~) і-ый элемент сообщает ~ е W., при этом r может быть не равным ~.
Теорема 5.3. [52] Прямой механизм распределения ресурса h(~), определяемый алгоритмом 5.1, является механизмом открытого управления. ¦