НЕМАНИПУЛИРУЕМЫЕ МЕХАНИЗМЫ ОБМЕНА В МНОГОЭЛЕМЕНТНЫХ АКТИВНЫХ СИСТЕМАХ
Данная глава работы посвящена исследованию механизмов ОУ в ОС с конечным числом элементов.
В раздел 3.1 рассматривается ОС с веерной структурой взаимодействия элементов и одним уровнем иерархии. Т.е ОС состоит из одного центра и конечного числа АЭ.
Для многоэлементных ОС, соответствующих многоэлементной задачи стимулирования строится эффективный механизм обмена ОУ.
В разделе 3.2 рассматриваются ОС со структурой взаимодействия элементов типа цепочка и одним уровнем иерархии. Предлагаются три метода построения неманипулируемых механизмов обмена для случая, когда общий метод неприменим.
Первый метод - метод консолидации АЭ - центр рассматривает всех АЭ как единый АЭ и решает задачу нахождения механизма обмена ОУ для полученной двухэлементной ОС. Второй метод - метод разбиения схемы - центр взаимодействует с каждым АЭ по отдельности.
Третий метод - метод доносчика - центр делегирует права промежуточного центра тому АЭ, который сообщит наилучшую оценку типов всех АЭ. Также приводится ОС со структурой взаимодействия элементов типа цепочка и одним уровнем иерархии, для которой возможно применение общего метода построения неманипулируемого механизма обмена.
В последнем разделе третьей главы обсуждается применение полученных автором теоретических результатов при решении прикладных задач.
Полученные автором результаты, содержащиеся в этой главе были опубликованы в работах [32,35,38,42]
3.1. Неманипулируемые механизмы обмена для обменных схем с веерной структурой взаимодействия агентов
Рассматриваемая нами обменная схема будет представлять многоэлементный вариант обменной схемы, рассмотренной в разделе 1.1 (см. рисунок 10).
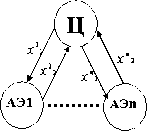
Рис. 10. Многоэлементная ОС с веерным типом взаимодействияагентов
бменная схема состоит из n +1 агентов - одного Центра и n АЭ. В системе имеется два типа ресурсов. Ограничения на ресурс примем
стандартными - A = y'j = Y}; j = 1,2}. Центр может обмениваться с
i=0
каждым из АЭ, АЭ не могут обмениваться между собой. Функции предпочтения имеют следующий вид:
(118) j( У:0, у) = y0 + H (у 2);
граничения индивидуальной рациональности достаточно просты -
IR(y0) = (i = .n j(Уі) j(Уі0)}.
Начальное распределение ресурсов задано следующим образом - весь ресурс первого типа сосредоточен у Ц, весь ресурс второго типа - у АЭ:
Y о
о у10
, Z у20 = Y2.
уи
i =1
Значения Y1 и Y2 выбираются таким образом, что бы рассматриваемая модель могла соответствовать определению обменной.
Запишем функции прибыли от обмена для центра:
(120) fo (x0, x2) = j (Y - x0, X) - j(Y ,0) = H (x20) - x0;
для АЭ:
(121) f (x1, x2) = ji(x1, у2 0 - x2) - ji(0, у2 0) = x1- e(x2, r)-Причем очевидно, что x = ^ xj, j = 1,2.
i=1
Следует отметить, что заданные ограничения ИР можно достаточно просто выразить через функции прибыли агентов от обмена:
IR={ fi (xt) 0; i = 0,n }.
Постановка задачи - найти механизм обмена ОУ p(s), максимизирующий ожидаемую прибыль центра от обмена -Ef (p(s)) ^max, при условии, что ему известны Q = [rmin,rmax] и вероятностное распределении типов АЭ - p(r), одинаковое для всех агентов.
Утверждение 10. Если функция предпочтения центра линейная, то неманипулируемый механизм обмена иметь следующий вид:
де
(ri) = e(xi2(ri),Г) - j (x2(t),T)dT, i = Yn;
J dr
x1
'min i
Z Y'. (r-i) = Yj, j = 1,2.
i =1
Доказательство. При выполненных условиях теоремы 1 для каждого АЭ можно записать его прибыль v(r,s_i) = J (xt(t,s_t),t)dT, i = 1,n.
r ¦ dri
'min '
Учитывая вид функций полезности АЭ, получаем, что
x1 (ri, s_i) =c(x2 (ri, s_i X r) _ J ^(x2 (t s_i ),t)dt, i =1 nr . dr
Очевидно, что функция предпочтения центра линейна, если H(y2) = ay2. Поэтому, функция полезности центра при использовании
неманипулируемого механизма обмена p(r) = (xf(r),x2(r),...,x(r),x2n(r)) будет иметь следующий вид:
Vo(r) = /с (Z 1(r X Z 2(r)) = Z V (r).
i =1 i =1 i =1
ri Qc
Где КО(r ) = a2(r ) _c( x2 (r, r_i), r) + J o-(x2(t, r_i),t)dt.
'min i
J dr
Следовательно, задачу максимизации ожидаемой прибыли центра можно представить виде задачи динамического программирования:
dc
x2(r,r_i) = argma J J [ox; _ c(x2,r) + J (x2,t)dt]P(r )p\r-l )dridr-i, i = Xn;
2 Q q^1
x2 (r, r_i) ? Y2 _ Z x2 (rj, r_,), xl (ri, r_i) ? Yi _ Z 1 (rj, r_,), i = X n ¦
n / i
Очевидно, что для i = 1, n функции x2 (r, r_t) имеют одинаковый вид. Причем их можно представить в следующем виде - x2 (r, r_) = x2 (r), где x2 (r) является решением задачи динамического программирования:
x,
i* i* I* dc
(r ) = argmax J J [ax2 _ c(x2 , r ) + J (x2 ,t)dt]P(ri )p'(r_i )drdr_i , i = 1
QQ
x~ J J / dr
x2(^ ) ? Y2 _Z 2(r, ) = Y2 (r_i ), i (ri ) ? Y1_Z i (r, ) = Y1(r_i ), i = 1 n¦
n/i
n/i
При этом Z Ylj (r_t) = Yj, j = 1,2. ¦
i =1
Иными словами, для рассматриваемой модели ОС с веерным типом взаимодействия агентов задача построения неманипулируемого механизма обмена эквивалентна задачи для ОС с одним АЭ. Задача построения эффективного и неманипулируемого механизма обмена разбивается на две задачи - задача построения эффективного и неманипулируемого механизма обмена для ОС с одним АЭ и задача оптимального распределения ресурсных ограничений между АЭ.
Поясним вышесказанное. Эффективный и неманипулируемый механизм обмена имеет следующий вид - p(r) = (p(~),...,Р(~)). p(r) = (xx(r),x2(r)) -эффективный и неманипулируемый механизм обмена для ОС с одним АЭ:
Функция полезности Ц - f0( хг, х2) = H (х2) - хг;
Функция полезности АЭ - f (xt, x2 ) = xt - c(x2, r);
dc
Хі(Г ) = C( x2(r X r ) -
(x2(r),t)dt,
dr
X2(r) = argmax Efofxjfx^x^r).
x2
r - назначаемый тип і-ого АЭ, задается следующим образом: ~ = min[r, r ]. Критические типы r определяются выполнением
ресурсных ограничений: ^ хх (r) = Y или ^ х2 (r) = Y2. Задача
і=1 і=1
оптимального распределения ресурсных ограничений между АЭ: ?о(Г)-®max, r = (r,...,r ).
r
Метод построения эффективных и неманипулируемых механизмов обмена для ОС с веерным типом взаимодействия агентов может быть проиллюстрирована на примере следующей задачи.
Задача 5. Построить эффективный неманипулируемый механизм обмена для ОС состоящей из центра и двух АЭ. Функции полезности от
і2
2
обмена центра - f0 (хх, х 2) = х 2
2r
і
r eQ = [rmin,rmax], i = 1,2. Ограничения x2 Y2. Центру известно, что
r - r.
max mm
распределение типов АЭ равномерно - F (r)
Механизм ОУ p(r) = (x 1i(r1), x 12(r1), x 2i(r2), x 22(r2)) имеет следующий вид -
p(r) =(p (~),p (~2)); r, r. e Q', r . e Q
г ’ г ? -г
maX[^ ,(rmax Y2 - r-i 2)1/2], r eW / Q r-i eW' , . = l2;
r ={
i max 2 -i
r , r. e Q / Q', r. e Q/ Q'
i -i
r Y
Q' = [rm.n, r], r = (-^r.
л 2 . /V 3 3
„ r. 4r. r .
2
max
6r
Здесь p(r) = (x1(r),x2(r)): x.2(r) =-^-, x. 1 (r.) = г min
Утверждение 11. Механизм p(r) = (p (~),p (r2)) является
неманипулируемым и оптимальным.
Доказательство. Очевидно, что неманипулируемый механизм обмена p (r) = (x1 (r), x2 (r)) является оптимальным для ОС с одним АЭ.
Задача оптимального распределения ресурсных ограничений имеет следующий вид:
2(ri3 + r23) - r
22
r + r
1 2 = Y
J- 0 .
3
min
?о(Гі, r2) = Y2
® max,
3r
2
max
1 '2
Yr
r = (^Г2.
Не трудно видеть, что r1
Задача оптимального распределения ресурсных ограничений является частным случаем задачи распределения ресурсов, для которой доказана оптимальность неманипулируемых механизмов планирования (см. теорема 5.3 [52]).
Используя метод множеств диктаторства [53] можно показать неманипулируемость предложенного метода определения назначаемых типов ~ и r2. На рисунке 11 решение задачи обмена представлено в графическом виде.
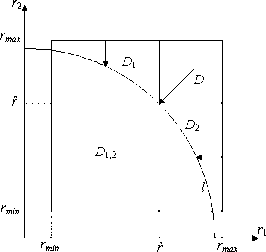
Рис. 11. Множества диктаторства
ОбластьD12: p(r) = (P(r1 ),P(r2)) - обоим АЭ назначаются планы в соответсвии с их заявками. Область D1: p(r) = (p(r),P(~)) - АЭ 1 является диктатором - назначаемые планы зависят только от его заявки. Область D2: p(r) = (P(~),P(r2)) - АЭ 2 является диктатором - назначаемые планы зависят только от его заявки.
Область D : p(r) = (Р(r),P(r)) - планы обоих АЭ не зависят от их заявок. Поэтому, в соответствии с теоремой
2.1.1 [53] предложенный метод определения назначаемых типов
неманипулируем. Следовательно, неманипулируем и весь предложенный механизм обмена. ¦ -
Полученные в данном разделе результаты, вероятно, могут быть перенесены на более общий вид модели ОС с веерной структурой взаимодействия агентов. Но это является предметом дальнейших исследований. Перейдем к рассмотрению ОС со структурой взаимодействия агентов типа цепочка
3.2. Неманипулируемые механизмы обмена для обменных схем со структурой взаимодействия агентов типа цепочка
Пример подобной ОС изображен на рисунке 12.
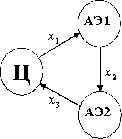
Рис. 12. Многоэлементная ОС со структурой взаимодействия агентов типа цепочка
С состоит из центра и двух АЭ. В системе имеются ресурсы трех типов. В обмен на получаемый от центра ресурс типа 1, АЭ1 передает АЭ2 ресурс типа 2. В свою очередь, АЭ2 в обмен на полученный от АЭ1 ресурс типа 2 передает центру ресурс типа 3.
Вид функций полезности от обмена:
(122) f0(x1,x3) = x3 - cx1 для Ц,
(123) /,(x15x2,r) = rx, - x2 для АЭ1,
(124) /1(x2, x3, r2) = r2x2 - x3 для АЭ2.
Ресурсные ограничения в терминах трансфертов имеют следующий вид А={xt е [0,1^],x2 0,x3 0}. Центру известны диапазоны возможных значений типов АЭ r eQi = [rt,r]. Задача центра - построить механизм обмена ОУ, максимизирующий его гарантированную относительную
®max, s = (у,s2) - вектор сообщений АЭ
прибыль от обмена min
/0(p(s))
/оЙе‘(^) оценок своих типов.
Лемма 6. Максимальный доход выражается:
(125) /0det(ri,r2) = (ГГ -c)^.
Доказательство. Действительно, руководствуясь принципом индивидуальной рациональности для активного элемента, получаем из (123) и (124), что r1x1 x2 и r2x2 x3. Поэтому /0,det (r;, r2) (r1r2 - c)x1 и
достигает максимума при x; = Y1. ¦
Рассмотрим различные методы построения неманипулируемого механизма обмена для предложенной ОС.
Метод консолидации АЭ.
Центр рассматривает всех АЭ как единый АЭ и решает задачу нахождения механизма обмена ОУ для полученной базовой ОС (см. рисунок 13.).
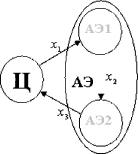
Рис. 13. Метод консолидации АЭ
Фактически мы рассмотрим взаимодействие центра с коалицией, состоящей из двух активных элементов. Пока мы ничего не предполагаем относительно того, как будут взаимодействовать АЭ между собой (т.е какой будет дележ). Но очевидно, что для любого положительного выигрыша данной коалиции найдется такой дележ, когда выигрыши обоих АЭ будут неотрицательны. Поэтому предположим, что для при любом плане обмена, предложенном центром, выигрыш коалиции от которого не отрицательный, оба АЭ не откажутся от участия в обмене. Устанавливать дележ между собой АЭ могут путем определения количества ресурса типа у, который АЭ1 передает АЭ2.
Таким образом трансферты в цепочке остаются прежними.
Лемма 7. Целевая функция коалиции записывается следующим образом:
(126) fn = Г1Г2Х1 - Х3.
Доказательство. Рассмотрим некий план (x1vx3), предложенный центром.
Предположим, что АЭ сообщили и или знают истинные значения обменных коэффициентов друг друга. Из (123) и (124) получим следующее выражения:
Х2 = Гі Xi -fi.
Следовательно
f2 = k2 (ki X -fi) - Z.
Следовательно
(127) f2 + kfi= k2 ki x - z.
В левой части выражения (127) стоит суммарный выигрыш обоих АЭ в размерности ресурса типа z, т.е. суммарный выигрыш коалиции, а правая часть совпадает с правой частью выражения (126).
Рассмотрим аналогичным способом ситуацию, когда оба АЭ взаимодействуют между собой на основании некоторых произвольных заявок 5,1=[rj,r1] и s2=[r2,г2]. Иными словами АЭ искажают информацию о своих обменных коэффициентах (очевидно с целью получения дополнительной прибыли). Тогда по аналогии с (127)
/2'+ sfi'= S2 Si Xi - X3,
гдеfi'иf2' "заявленная" прибыль АЭ. Но из (123) и (124)
X2 = ri Xi -f 1;
X3 = Г2 X2 -fi.
Где fi и f2 - полная прибыль каждого из АЭ. Следовательно выражение
(127) будет выполняться для истинных значений прибыли участников коалиции:
f2 + rfi= Г2 Гі Xi - X3.
Тем самым мы доказали, что целевая функция коалиции записывается выражением (126). ¦
Т. е. мы получили обменную схему состоящую из центра с функцией полезности (122) и одного АЭ с целевой функцией (126). Центр знает диапазон возможных значений обменного коэффициента АЭ W=[ r 1 r 2, rlr2\.
Используя построенный в главе 1 неманипулируемый механизм обмена для задачи 4, построим механизм открытого управления [xi(s),xs(sj\., где S=S!S2.
(128) *i( s) = Yi;
m( s)
Ж;
(129) x3(s) = m(rir2)(s-c(1
m( s)
где (130) m(s) = [i + in s c \-1.
r 1 r 2 - c
Функция полезности центра при использовании данного механизма записывается как
(131) /оА s2) = m(r1r2)(s1s2 - C)Y1-
Утверждение 12. Оптимальные заявки для коалиции будет s*=rlr2.
Доказательство. Из (126), (128), (129) и (130) следует, что
а/12 = m(r-r2)s-(r1 r2 - s1sY1, І = 1,2-
ds
d2 /1
s1s 2 - c
s- (rr2 - c)
= -m(r1r2)-Y'
12
dyds2 s1 s2 - c
Таким образом, видно, что максимум / достигается при sls2=rlr2 , так
5/12-П „ 5 2/12
12
ds1ds2
0 при si=rlr2/ s-i.u
0, а
как для si
ds.
Следовательно, построенный механизм обмена (128) - (130) можно назвать механизмом открытого управления для коалиции. Но данный механизм нельзя назвать полным, т. к. он не определяет размер трансферта ресурса типа 2. Предполагается, что коалиция АЭ сама сумеет поделить полученный ею выигрыш от обмена.
Рассмотрим, каким образом можно ввести в механизм обмена (128) -(130) зависимость размера трансферта ресурса типа 2 от заявок игроков.
Утверждение 13. Не существует такой функции x2(s1,s2), для которой выполнялись бы следующие требования:
Г = argmax/(у, ^);
si
Г2 = argmax /2(si, s2).
s2
Доказательство. Для выполнения приведенных в утверждении требований необходимо, чтобы x2(sj,s2) удовлетворяла следующей паре
fif fif
дифференциальных уравнений: (r1, s2) = 0 и (s1, r2) = 0.
ds1 ds2
С учетом формул (128) - (130) получаем, что
fix s s
(132) -ЧуS2) = m(rlf2)Yl -1-2-;
GS1 S1S2 - C
2
s1
S1S2 - C
fix2
fiS2
(133)
(s1 s2) = m(r1r2)Y1
Из (132)
получаем
-m(r1r2)Y1 (s1s
получаем
fix2
fis1fis2
s1C
(S1 s2) =
C)
Из (133)
5x2 2yc - у s2
2 (s1s2) = -m(r1r2)^-x 1 2
(S1S2 - C)
fiy ф fiy
fis2 fis1
Поэтому не
Следовательно
существует такой удовлетворяющей
ds1ds2 ds2ds1
непрерывно-дифференцируемой функции x2(s1,s2), требованиям утверждения. ¦
Рассмотрим, как может повлиять назначение центром размера трансферта ресурса типа 2 в зависимости от заявок игроков, исходя из предположения, что АЭ поделят выигрыш от обмена поровну:
(134)rf .
( 1 1) ае (--^).
x2
Лемма 8. При дележе выигрыша f2= rf максимум функций полезности каждого АЭ будет достигаться при тех же заявках, при которых достигается максимум выигрыша коалиции, т.е. при s1s2*=r1r2.
fi
Доказательство. Из (127) и (134) следует, что Г r2 Х1 - x3 _ f 12 .
2r
2r
f = rir2X1 - X3 _ fn
1 2 2 ‘
В соответствии с утверждением 12, максимум значений целевых функций АЭ будет достигаться при s1s2=r1r2.rn
Трансферт ресурса типа 2, соответствующий дележу (134) можно записать следующим образом:
(135) r2)
r1r2 Х1 + Х3
2r2
Но центру не известны истинные значения r2 и r2. Поэтому для центра выражение (135) записывается следующим образом:
S 2 Х1( S) + Х2( S)
2S 2
(136) Х2( S = S1 S2)
К сожалению, механизм обмена, определяемый (128), (129) и (136) не является механизмом обмена открытого управления, так как для каждого АЭ в отдельности сообщение истинного значения своего обменного коэффициента не является доминантной стратегией. Более того, верно следующее:
ds.
г
’ ds .
0, i = 1,2.
Хотя утверждение 12 выполняется и для данного механизма.
В качестве решения данной проблемы, можно предложитьследующую модификацию механизма обмена (128), (129) и (136),основанную на механизмах Маскина [66] и МакКельви [83] - каждый АЭсообщает центру оценки как своего обменного коэффициента, так икоэффициента другого АЭ - {s^s.^-}. В случае совпадения заявок от обоихАЭ, центр назначает им план по (128), (129) и (136) в соответствии с 102 сообщенными ему заявками.
В случае не соответствия заявок - s1j^s1,2 или s2j^s2'2, центр выбирает некоторый произвольный план, основанный на представленных заявках, например у = max[sii,у_г ], i = 1,2. Т.е.
выбираются максимальные из сообщенных заявок. Необходимо заметить, что и для такой модификации механизма обмена (128), (129) и (136) утверждение 12 верно.
Для механизмов Маскина и МакКельви предполагалось, что АЭ полностью информированы о параметрах всех участников АС. Для нашего механизма можно ввести такое же допущение, либо предположить, что АЭ как-то информируют друг друга о своих параметрах в ходе их коалиционного взаимодействия.
Метод разбиения схемы
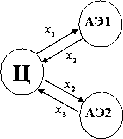
Рис. 14. Метод разбиения схемы
Для данного способа необходимо разбить первоначальную схему на две подсхемы (см. рисунок 14). В первой подсхеме центра дает АЭ1 некоторое количество ресурса типа 1 , и забирает от него некотрое количество ресурса типа 2. Во второй подсхеме центр дает АЭ2 некоторе количество ресурса типа 2, а получает некоторое количество ресурса типа 3.
Лемма 9. Для обеспечения максимальной эффективности функционирования данной схемы центру необходимо передать АЭ2 все количество ресурса типа 2, которое он получил от АЭ1.
Доказательство. Из (122) следует, что прибыль центра не увеличивается с ростом наличия у центра ресурса типа 2, в то время, чем меньше ресурса этого типа Ц передаст АЭ2 тем меньше он сумеет получить ресурса типа 3. Следовательно центру, для повышения эффективности обмена, необходимо передавать АЭ2 весь ресурс типа 2. ¦
С учетом вышесказанного запишем целевые функции всех участников обмена следующим образом. Для первой подсхемы:
(137) foi = ax2 - cxi;
fl = Г1 Xi - X2.
Для второй подсхемы:
(138) fo2 = X3 - 0X2;
f2 = Г2 X2 - X3,
где a - произвольным образом введенный обменный коэффициент для центра по ресурсу типа 2. Легко видеть что для ?а(137) и (138) в сумме дают (122).
Но для правильного построения механизмов открытого управления для каждой из подсхем необходимо ввести следующие ограничение на о :
c
(139) ае (, r 2).
r 1
Множество возможных значений о не пусто при выполнении условий
Г1 r 2 c.
Теперь перейдем к построению механизмов обмена для обоих подсхем.
Для первой схемы все достаточно просто - это простая задача классического обмена, рассмотренная в разделе 1.2. При рассмотрении второй схемы мы сталкиваемся с большими трудностями - центру необходимо отдать АЭ2 весь ресурс типа и сохранить неманипулируемость механизма обмена.
Введем следующую зависимость плана обмена для первого АЭ от заявки второго:
mir) m2(r2) Y.
m(si) m2(s2) 15
(140) у( у, у)
C (1__L_) m2(r2) Y
a mCO m2(s2) 1
(141) Х2(У S2) = Ml(ri)(S1
где
, 4 r„ , s. - c/a_
(142) m (sx) =[1 + In -] ;
r j - c/a
S2 ~ a ]_1 r 2 _ a '
(143) ju2(s2) = [1 + ln
Формулы (140) и (141) представляют механизм обмена ОУ для задачи
тЖ)
классического обмена, помноженные на
*2 У 2 -
тЖ2)
Обозначим
c1
(144) Y2(у) = ml(rl)(sl - -(1--))Y1.
a MW
Тогда (141) можно переписать следующим образом:
(145) x2(s„ s2) = У) Y2( s,).
m( s2)
Выражение (145) аналогично выражению, определяющему первую компоненту плана обмена в механизме обмена ОУ для задачи классического обмена. Отсюда следует, что вторую компоненту плана обмена для АЭ2 можно будет записать следующим образом:
(146) хз(У s2) = тЖ2Ж2 _ a(1--^)Y2(s1).
m2(s 2)
Выражения (140), (141) и (146) являются механизмом обмена между центром и двумя АЭ, полученным методом разбиения схемы, так как полностью определяют трансферты всех ресурсов в системе.
Утверждение 14. Механизм обмена, определяемый выражениями (140), (141) и (146), является механизмом открытого управления.
Нам необходимо показать, что максимум целевых функций обоих АЭ будет достигаться при сообщении ими истинных значений своих обменных коэффициентов. Из (123), (140), (141) и (146) следует, что
S s,, ,2) = йЩ m(r-) JL-5_;
оу m(s2) s - c /_
d2 f, X m2(r2) ,_4 T - c/_
(s2) = -^^-
(S1 - c / _)
ds
OS1- (S1, S2) = Y2 (S1 )й2 (Г2 ) T-2^ ; ds1 s2 - _
0 ^ (S1 , S2) = -Y2 (S1 )й2 (T2 kl _
ds; 4 ^ * ^2 -_)
Следовательно, с учетом ограничений модели и (139), получаем, что максимум функции полезности АЭ1 достигается при s1=r1 , для АЭ2 - при
S2=r2-rn
Сравним эффективности механизмов, построенных в данной и предыдущей главах - (128), (129) и (140), (141), (146). Эффективность неманипулируемого механизма обмена, полученного первым методом записывается:
K1 = m(T1T2);
Полученного вторым методом -
m1(T1)m2(T2)
(Г1Г2 - С)
(147) K 2
(T1
))(Т2 - _(1
))
й2(Т2)
Проанализируем полученные выше выражения.
Лемма 10. ?т15 т2, удовлетворяющим ограничениям модели, верноследующее - 1. mte) m(r1 X mte) m(r2 ^ 2. mte) ^ m (r (T2).
Доказательство. С учетом ограничений на параметр а получаем следующие неравенства:
T - c/_ t r2 - c - c(r2 /_ -1) t r2 - c TjT2 - c r1 - c/_ ri T2 - c - c(r2/_- 1) r1 r2 - c ri T2 - c ’
r2 - a rj r2 - c - (ra - c) rj r2 - c rj r2 - c
Из полученных выше неравенств очевидным образом следует, что m(kjk2)m(K) и m(kjk2)М2(к2)-
Для доказательства второго утверждения рассмотрим следующую функцию
м (rj r2) = m(rj r2)/ mj(rj)m2(r2)-
Очевидно, что M (r j r 2) = 1. Кроме того,
om m( ч2)
(rir2) = 12
or
mj(rj) rm( r1r2)
Ml( ri)M2(r2)
12
r - c/a rr - c
m(rir2)2 c(r2/a- j)
dM
dr
(rir2)
0;
mj(ri)m2(r2)(ri- c/aXrir2- c)
m2(r2) riM(rir2)
ом( ) mte)
(rir2) =-
dr2
Мі(Г1)М2(Г2)
m(rir2)2 (ria - c)
r2 - a rir2 - c
dM
(rir2)
0.
Or2^ Ml (ri )М2 (r2 )(r2 - a)(ri r2 - c)
Следовательно Ju(r1 r2) jU1(r1)m2(r2), так как функция M(r1r2)-возрастающая. ¦
Далее, можно показать, что
c 1 1 c
(r - - (1--))(r2 - a(1--))----
a M1(r1) M2(r2) M1(r1)M2(r2)
= rr + c(1--1---1) - ra(1
(148) M1(r1) M2(r2)
1 N c 1 S ^ 1 ,
) - r1(1--) - r2 (1--~)
r1r2 + c(1 -
MM M2(r2)
M2(r2)
mM'
r1r2 - c
Утверждение 15. Консолидированный неманипулируемый механизм обмена обладает большей эффективностью, чем неманипулируемый механизм обмена, полученный методом разбиения схемы.
Доказательство. Из неравенства (148) следует, чтоK2 jul{rl)m2{r2). А из Лемма 10 - K2 ? m(r1r2) = ?)- ¦
Но механизм (140), (141), (146) однозначно задает трансферты ресурсов всех типов в обменной схеме и побуждает АЭ сообщать центру истинные значения обменных коэффициентов, а не результирующего обменного коэффициента, как в механизме (128), (129) (или в его модификации (128), (129) и (136)), что может быть актуальным в отдельно взятых обменных схемах.
Метод доносчика
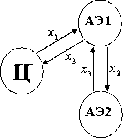
Рис. 15. Метод доносчика
Данный способ подразумевает, что центр каким-то образом присваивает одному из АЭ роль промежуточного центра (или посредника) и назначает ему некий план обмена. Посредник, в свою очередь, назначает некий план обмена между собой и оставшимся АЭ (см рисунок 15).
Не трудно показать, что в случае полной информированности обоих АЭ и отсутствия возможности их кооперации данный способ позволяет устранить неполную информированность центра и свести задачу обмена к детерминированной. Данный механизм обмена выглядит следующим образом:
Центр просит каждого из АЭ сообщить свою оценку их общего обменного коэффициента r2 r1. Затем центр выбирает АЭ, сообщившего наибольшую оценку, и назначает ему следующий план обмена
(149) Xi=Yi; X3=Si Yi,
где i - номер АЭ, которого центр назначил посредником. Так как посредник обладает полной информированностью относительно параметров другого АЭ, то он решает детерминированную задачу обмена:
(150) X2=s1/r2Y1; хз= sjYj, если посредник - АЭ1 и
(151) Xi=Yi; X2=riYi, если АЭ2.
Очевидно, что всю прибыль от обмена между элементами получает посредник. Следовательно, каждый из АЭ будет стремится сообщить максимально возможную заявку.