РАСПРЕДЕЛЕНИЕ ПРЕМИИ В НЕОДНОРОДНОМ КОЛЛЕКТИВЕ
В основе этой процедуры лежит следующее рассуждение. Показатель rі характеризует квалификацию i-го элемента. Чем выше квалификация элемента, тем больший объем работ он выполняет, или выполняет работу за более короткое время или на более высоком уровне качества. Однако в силу того, что такой способ формирования КТУ не учитывает реальный вклад каждого элемента в результаты деятельности всего коллектива, из (30) сразу следует, что рассматриваемая процедура формирования КТУ не побуждает элементы системы повышать эффективность работы.
Естественный и простейший способ определения КТУ и соответственно, вклада i-го элемента в результаты деятельности всего коллектива - пропорционально показателю эффективности xi. В этом случае
d. = ^ (31)
!,
j=i
Отсюда следует, что целевая функция каждого элемента зависит как от показателя эффективности, которого он смог достичь, так и от показателей эффективности, которые были достигнуты остальными элементами системы. Таким образом, исследуемую ситуацию можно рассматривать как игру n лиц с функциями выигрыша вида (32). Эффективность функционирования системы оценивается по суммарному показателю эффективности в ситуации равновесия по Нэшу [13]. Для нахождения значений показателей эффективности х: в ситуации равновесия по Нэшу необходимо решить систему уравнений
j
9X:
? xj-¦
(32)
Ф - kX: .
2,-
J=1
-Ф - к = 0
J=1
? xj
=1
Отсюда
Ф(п -1) kn2
(33)
X: =
что означает, что в ситуации равновесия все элементы достигают одинаковых показателей эффективности, и соответственно,
Ф(п -1) kn
*
X j = nX =
(34)
j=i
Значение целевой функции і-го элемента определяется выражением
Ф
j і = n
Из (33) видно, что чем больше премиальный фонд, тем больше показатель эффективности і-го элемента.
Но вполне естественно считать, что начиная с некоторого значения Ф, рост показателя эффективности і-го элемента прекратится, так как вполне естественно предположить, что каждый элемент
61
ограничен своими физическими возможностями. В дальнейшем будем считать, что максимальный показатель эффективности, которого может достигнуть элемент, для всей системы одинаков и обозначается через xma, то есть xi ? xmax.
В работе рассматривается случай
- kxma 0 .
n
Нетрудно определить минимальный размер премиального фонда Фmin, который будет стимулировать все элементы максимально повышать показатели эффективности работ.
Для однородного коллектива Фmin находится из условия
* max
xi =x , откуда
(35)
n2kxmax
min
(n -1
Дальнейшее увеличение размера премиального фонда не дает никакого эффекта, поскольку элементы не могут работать выше своих возможностей.
При проведении игрового эксперимента была рассмотрена деятельность подразделений фирмы, состоящей из пяти человек, т.е. n=5.
Пусть Ф=2000; кі=к2=к3=к4=к5=4. Роль участников игрового эксперимента здесь выполняют автоматы. Их параметры: у}=0,3; g2=0,5; g3=0,4; Y4=0,6; Js=0,7. Из (32) нетрудно определить положение цели i-го автомата. В к-й партии оно определяется выражением
Теоретико-игровой анализ модели показал, что в ситуации равновесия показатели эффективности игроков равны
xi =x2 =x3 =x4 =x5 =80.
На рис. 19 приведены графики изменения стратегий участников игрового эксперимента. А на рис. 20 график, изменения суммарного значения показателя эффективности.
Из графика на рис. 19 следует, что, аналитические результаты, практически, полностью соответствуют результатам игрового эксперимента.
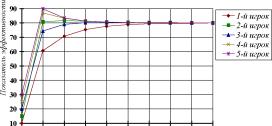
Рис. 19.
А график на рис. 20 показывает, что уже к десятой партии суммарное значение показателя эффективности соответствует его значению в ситуации равновесия по Нэшу.
| 420 -I |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
8
т |
| 380 |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| 300 |
|
|
|
|
|
|
|
|
|
| 260 |
|
|
|
|
|
|
|
|
|
| 220 |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
4 |
1 |
0 1 |
3 1 |
6 1 |
9 2 |
4 ^Г
1
. N |
5 2
р парт |
|
| Рис. 20. |
Теперь ставится вопрос. Возможно ли достигнуть более высоких результатов деятельности в однородном коллективе, не увеличивая фонд премирования Ф?
Один из подходов к решению этой задачи заключается в следующем. Предположим, что коллектив, состоящий из n элементов, разбит на m подколлективов по п- элементов в каждом, Соответственно, фонд Ф разбит на m подфондов Фj, j=1,...,m. Из (32) следует, что в ситуации равновесия по Нэшу показатель эффективности элемента, входящего в j-й подколлектив, можно записать как
Ф-(П- - 1) kn2
Соответственно, суммарный показатель эффективности работы всего j-го подколлектива равен
njxj =
Фj(ni -1)
Наконец, суммарный показатель эффективности всего коллектива определяется выражением
= Ф 1 g ф,
k kj=1nj
и- =1ІФ
j=1 kj=1
1-
V nj 0
(36)
Теперь необходимо рассчитать, какое количество элементов должно находиться в каждой подгруппе, чтобы суммарный показатель эффективности достигал максимального значения. Формально запись этой задачи можно представить в виде
m ф .
Z ® min
j=1nj
m
Z n, = n
(37)
j=1
Решая эту задачу, получаем
(38)
n.
nj =
j=1
Будем считать, что Ф}- таковы, что nj -целые числа. Подставляя в (36), выражения для nj из (38), получим значение суммарного показателя эффективности коллектива
(39).
Сравним теперь суммарный показатель эффективности до разбиения однородного коллектива (34) с суммарным показателем эффективности, который получается после разбиения коллектива на m подколлективов (39).
Предположим, что
Ф(n -1) Ф 1 Г m
kn к kn
тогда
или
\j=1 0
Равенство имеет место только в случае, когда m=1. Во всех остальных случаях
Следовательно, разбиение однородного коллектива не приводит к увеличению суммарного показателя эффективности работ.
Пусть количество элементов изменилось и стало равным (n-1), то есть из коллектива ушел элемент под номером n, а размер премиального фонда остался прежним (не уменьшился). Покажем, каким образом уход из коллектива одного элемента влияет на суммарный показатель эффективности работы коллектива.
Используя выражение (34), определим суммарный показатель эффективности, который выполняет коллектив с количеством элементов (n-1) в ситуации равновесия
j * _ Ф(п - 2) j _і j k(n -1)
Легко показать, что
Ф(п - 2) ? Ф(п -1) k(n -1) kn
Следовательно, сокращение однородного коллектива приводит к уменьшению суммарного показателя эффективности работы.
При этом нетрудно видеть, что показатель эффективности отдельного элемента возрастает.
Наконец, ставится следующая задача. Возможно ли повысить суммарный показатель эффективности однородного коллектива, не увеличивая фонд премирования Ф, но по-другому формируя КТУ элементов?
Пусть КТУ определяется выражением
xa
8г _ V, где a1. (40)
j
j_1
Тогда для нахождения равновесной ситуации по Нэшу имеем
,2 a-1
axa-1( j xa - oxf-1)
j_1
¦x Ф - k _ 0 , г = 1,...n
a2
( j xj)
j_1
или
2a-1
a-1
k
аФ
xi
xi
(41).
i = 1,...n
jxa (jxj)2
j_1
j _1
Предположим, что в силу однородности коллектива, в ситуации равновесия по Нэшу показатели эффективности xi будут у элементов одинаковы. Следовательно, из (41) имеем
X, = а
Ф(п -1) кп2
Сравнивая (34) и (42) можем утверждать, что при а1 в ситуа-
- * *
ции равновесия по Нэшу x x .
Здесь следует отметить, что все приведенные выше рассуждения справедливы для случая, когда возможности элемента по повышению показателя эффективности не ограничены. Однако вполне естественно предположить, что на физические, умственные, эмоциональные и временные затраты существуют ограничения, обусловленные индивидуальными возможностями каждого элемента. В связи с этим можем считать, что максимальное значение показателя эффективности i-го элемента равно ximax. И соответственно, выводы, полученные выше, справедливы для случая X* ? хт^ .
Если для заданного а окажется, что xt xma, то в этом случае i-й элемент может обеспечить достижение лишь показателя
эффективности хмса. Отсюда можно найти значение Omax, при кото-
- *
* _ max
ром x = x .
Действительно, из (42) следует, что
2 **
nx
аФ
nx
или
Ф(п -1) кп
Z*
Xj = а
(42)
j=і
соответственно,
a max =
kxmaxn2
Ф(п -1)
Другое ограничение на значение а можно вывести из следующих соображений.
В ситуации равновесия значение целевой функции i-го элемента определяется выражением
Ф п 1 j, = (1 - а-) 0.
Поэтому
a .
n -1
Таким образом, использование процедуры (40) для формирования КТУ i-го элемента позволяет увеличить суммарный показатель эффективности коллектива на величину
a Wn - 1) - ФО,- 1) = Ф(п - V (a -1) . kn kn kn
Соответственно, процент увеличения определяется величиной
h = a -1 = - ,
n -1
то есть, если коллектив состоит из 11 человек, максимально суммарный показатель эффективности можно увеличить на 10%.
При решении системы (41) было сделано предположение, что для однородного коллектива в ситуации равновесия показатель эффективности у всех элементов одинаков. Проверим это предположение путем проведения игрового эксперимента.
Условия эксперимента те же, что были в примере, рассмотренном ранее, но КТУ определяется в соответствии с выражением (40) и a=1,2. Положение цели автомат находит из решения уравнения
a-1
¦ 2
ОФ Е xa = Е XT + X,
j *i
j*i
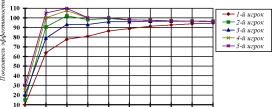
А на рис. 22 график изменения суммарного значения показателей эффективности автоматов.
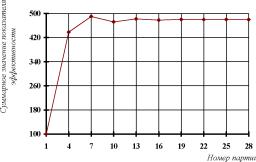
Формальный анализ модели показал, что в ситуации равновесия показатели эффективности автоматов равны:
x1 =x2 =x3 =x4 =x5 =96.
Из графика, изображенного на рис. 21, видно, что автоматы сошлись в ситуацию
x*=94,4; x2*=96,45; x3*=96,28; x4=96,38; x3=96,31.
Следует отметить, что значения показателей эффективности в имитационном эксперименте, полученные за двадцать восемь итераций отличаются от показателей эффективности, рассчитанных теоретически, всего на 1,5%.
РАСПРЕДЕЛЕНИЕ ПРЕМИИ В НЕОДНОРОДНОМ КОЛЛЕКТИВЕ
Для неоднородного коллектива целевая функция i-го элемента записывается в виде
j=80-kiXi.
Пусть 8І i-го элемента формируется в соответствии с (31). При этом целевая функция i-го элемента имеет вид
X
j = -^~ Ф - kiXi, (43)
Zxj
j=1
В каждом периоде функционирования элементы стремятся достичь таких показателей эффективности работы, чтобы увеличить значение своей целевой функции. Нетрудно показать, что для функции вида (43) существует ситуация равновесия по Нэшу.
Решая систему уравнений
X xj- x
0, i = 1,...n,
ЭХ:
(44)
( П Y
Xx,
V j=1 получаем
Ф(п -1)
n
Xkj
j=1
Отсюда показатель эффективности i-го элемента определяется выражением
Xkj -кі(п-1)
X* = ^п-Ф(п -1) , i = 1,...,п (45)
(Х?2
j=1
При проведении игрового эксперимента также рассматривалась деятельность подразделений фирмы, состоящей из пяти чело-
век, т.е. n=5. Фонд так же не изменился Ф=2000. Роль участников игрового эксперимента выполняли автоматы с те ми же параметрами, что и выше рассмотренном эксперименте. А вот значения коэффициентов затрат поменялись следующим образом: k1=3; k2=k3=k4=4; k5=5. Положение цели i-го автомата в k-й партии определялось выражением
Теоретико-игровой анализ модели показал, что в ситуации равновесия показатели эффективности игроков равны
x1 =160; x2 =x3 =x4 =80; x5 =0.
На рис. 23 приведены графики изменения стратегий участников игрового эксперимента. А на рис. 24 график, изменения суммарного значения показателя эффективности.
Из графика на рис. 23 следует, что, аналитические результаты, практически, полностью соответствуют результатам игрового
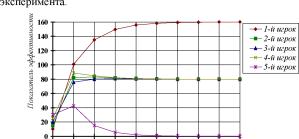
Из (44) следует, что суммарное значения показателя эффективности коллектива определяется фондом премирования Ф и
П
суммой коэффициентов затрат М kj . В двух последних экспери-
j=1
ментах и фонд и сумма коэффициентов оставались неизменными, но сами значения к, изменились. Как следствие, суммарное значение показателей эффективности элементов в ситуации равновесия по Нэшу не поменялось, но поменялись равновесные значения показателей эффективности элементов. Это хорошо показал график изменения стратегий на рис. 23.
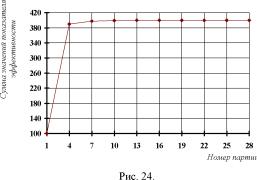
А график на рис. 24 показывает, что уже к десятой партии суммарное значение показателя эффективности соответствует его значению в ситуации равновесия по Нэшу. Сравнивая графики на рис. 22 и на рис. 24 можно утверждать, что суммарное значение показателей эффективности изменялось в обоих экспериментах практически одинаково.
Предположим, что коллектив состоит из р-лидеров и (п-р) рядовых элементов.
Пусть к - коэффициент затрат лидера, к - коэффициент затрат рядового элемента, соответственно, причем к кр .
Полагаем, что к1=к2=...=кр=кл и кр+1=кр+2=...=кп=к. Тогда
X к2 = X к + X к2 = ркл + (п - р)кр .
j=1 І=1 j=p+1
Используя выражение (44), найдем показатель эффективности рядового элемента хр в равновесной ситуации 72
Ф(п -1)
п-1
xp = ¦
(46)
pkp + (п - p)kл
pkp + (п - p )k1
Соответственно, показатель эффективности лидера хл определяется выражением
Ф(п -1)
п-1
1 - kp
(47)
pkp + (п - p )kл
pkp + (п - p )kл
Используя выражение (44), найдем суммарный показатель эффективности коллектива
pxл + (п - p )xp =
(48)
Ф(п -1)
pkл + (п - p)kp Если в (31) положить k=kp, то сравнив (46) и (33) нетрудно показать, что xp Xj , то есть появление в коллективе лидеров (более
квалифицированных) вынуждает рядовых (менее квалифицированных) элементов снижать показатель эффективности работ.
Понятно, что снижение показателя эффективности рядовыми элементами влечет за собой и уменьшение значения их целевой функции. Но, кроме того, если бы показатель эффективности рядовых элементов остался таким же, каким он был до разбиения коллектива на p-лидеров и (п-p) рядовых (то есть не снизился), то значение целевой функции рядовых элементов уменьшилось бы еще больше.
А из (46) получаем, что если количество лидеров в коллективе таково, что
kp
kp - kл
, kn
или p 1 +--,
kp - kл
то рядовым элементам вообще не выгодно увеличивать показатель эффективности работы.
При этом (47) принимает вид
хл = Ф(p -1) p2k
Однако при p=1, то есть если в коллективе есть только один лидер, рядовым элементам всегда выгодно увеличивать показатели эффективности работы.
В то же время легко показать, что появление в коллективе лидеров приводит к повышению суммарного показателя эффективности работ всего коллектива, несмотря на снижение показателей эффективности работ рядовыми элементами, то есть справедливо неравенство
_Ф(п -1)_ ф(п -1) (49)
ркл + (п - р)кр крп
Действительно, из (49) следует, что
крп ркл + (п - р)кр
или
р(кр - кл ) 0.
Так как кркл, то отсюда и следует справедливость неравенства
(49).
Определим минимальный размер премиального фонда Фтіп, который будет стимулировать все элементы максимально повышать показатели эффективности работ.
Если коллектив однороден, то все элементы имеют одинаковый коэффициент затрат к, и соответственно справедливо (33). Определим Фтіп, при котором хр=хта.
max _ Фтіп(п - 1)
кп2 ,
откуда
кп2хтах
Ф ¦
тіп
Предположим, что предел физических возможностей как рядового элемента, так и лидера, одинаковы, то есть максимальный показатель эффективности работ равен хтах.
Из сравнения (46) и (47) следует, что хлхр. Поэтому для того, чтобы лидеры вышли на предел своих физических возможностей, требуется меньший фонд стимулирования.
Пусть Ф таково, что хл=хшас, а хрхтах. В этом случае из (32) целевая функция рядового элемента может быть представлена в виде
Тогда в равновесной ситуации по Нэшу показатель эффективности рядового элемента равен
X,
Ф - kpx,.
j i=п-5
Z Xj + pxn
J=1
p xmax
п- p
x=-
(п - p - 1)Ф+д/(п - p - 1)2Ф2 + 4рХпсо:Ф(п - p)kp
2(п - p)2kp
Теперь можно определить значение Фтіп, при котором рядовой элемент неоднородного коллектива выходит на максимум своих физических возможностей. В этом случае
(п - p-1)Фт„+1(п - p-1)ФПп1п+4pXnWXPmJn - p)kP
2(п - p)2kp
max
X :
xma
п- p
Из
этого выражения нетрудно получить
kpп2хтах
(50)
Ф ¦ =
т,п
п-1
Дальнейшее увеличение размера фонда не дает никакого эффекта, поскольку выше своих возможностей элементы работать не могут.
Из сравнения (35) и (50) видно, что в неоднородном коллективе минимальный размер премиального фонда, который стимулирует все элементы системы максимально увеличивать показатели эффективности работ, остается таким же, что и для однородного коллектива.
Покажем, возможно, ли дальнейшее увеличение показателей эффективности работ в коллективе в рамках того же премиального фонда Ф.
Разобьем неоднородный коллектив на два подколлектива. Пусть первый состоит из p-лидеров, а второй состоит из (п-p) рядовых элементов. То есть при этом мы получили два однородных коллектива. Соответственно разобьем премиальный фонд Ф всего коллектива, именно: Ф=Фл+Ф1’. Тогда в положении равновесия по Нэшу суммарный показатель эффективности первого подколлектива равен
Фл (p -1)
Px1 =
кл p
Суммарный показатель эффективности второго подколлектива равен
(п - p)xp = Ф Р(п - P -1.
2 кр(п - р)
Соответственно, общий показатель эффективности всего коллектива из п элементов равен
К + (п - pM = М +
к p kp (п - p)
Выше было показано, что разбиение однородного коллектива на несколько подколлективов не приводит к увеличению суммарного показателя эффективности. Для неоднородного коллектива это не так.
Пусть
Фл(p -1) Фp(п - p -1) (Фp + Фл)(п -1)
кл p кр(п - p) pkл + (п - p)kp
В результате ряда преобразований получаем
кл кл
(п - p)(1 - ) +
V
л
к2 P Фл V
--
Ф Р
(51)
кл кл
p(1--) +--
и
(п - P)2
Таким образом, разбиение неоднородного коллектива на два подколлектива приводит к увеличению их суммарного показателя эффективности работы, если справедливо (51).
Неравенство (51) приобретает более простой вид, если p = 2 то есть в коллективе находится половина лидеров и половина рядовых. Тогда неравенство (51) может быть записано в виде
Фл кл
Ф Ф.
А так как 1, то разбиение фонда Ф пополам приводит к кр
увеличению суммарного показателя эффективности работ.
Выше было показано, что сокращение однородного коллектива приводит к уменьшению суммарного показателя эффективности работы коллектива. Рассмотрим данную задачу для неоднородного коллектива.
Пусть количество элементов в неоднородном коллективе изменилось и стало равным (n-1), то есть из коллектива ушел элемент под номером п, а размер премиального фонда остался прежним (не уменьшился). Покажем, каким образом уход из бригады одного рядового элемента влияет на суммарный показатель эффективности работы коллектива.
Используя выражение (48), определим суммарный показатель эффективности, который выполняет коллектив с количеством элементов (п-1) в ситуации равновесия
n^x*J =-Ф(п^2_- (52)
j=1 J ркл + (п - р -1 )кр
Сравнив выражения (52) и (48) в результате ряда преобразований имеем
кі Р-1
кр р
кл
или - 1
кр
(53)
Таким образом, уход из неоднородного коллектива одного рядового элемента приводит к повышению суммарного показателя эффективности работы, если выполняется условие (53).
ЗАКЛЮЧЕНИЕ
В работе рассмотрены базовые модели и механизмы внутрифирменного управления. Использование таких механизмов в практике управления фирмой позволит выявить их внутренние резервы, что позволит достичь более высоких результатов с меньшими затратами. Естественно, что описанные здесь механизмы не охватывают все моменты, необходимые для управления фирмой, однако их применение может служить основой для принятия правильных решений.
Обоснованность принимаемых управленческих решений существенно повышается, если при этом используется метод имитационных игр, позволяющий, с одной стороны, проверить на модели правильность принятого решения, а с другой, служит средством обучения. В работе приведены результаты ряда имитационных игр, с помощью которых проверяются или обосновываются принимаемые решения.
Одной из задач дальнейших исследований является развитие базовых моделей и механизмов на более сложные и реальные ситуации.
ЛИТЕРАТУРА
1. Бурков В.Н., Трапезова М.Н. Механизмы внутрифирменного управления. М., Институт проблем управления, 2000.
2. Дьяченко М.А. Внутрифирменное планирование: Учебное пособие для вузов/ ГУУ. - М.: ЗАО Финстатинформ,
1999.
3. Герчикова И.Н. Менеджмент: Учебник. - М: ЮНИТИ,
2000.
4. Гибсон Дж.Л., Иванцевич Д.Л., Доннелли Д.Х. - мл. Организации: поведение, структуры, процессы: Учебник для вузов. - М: ИНФРА-М, 2000.
5. Смирнов Э.А. Основы теории организации: Учебное пособие для вузов. - М.: Аудит, ЮНИТИ, 1998.
6. Ануфриев И.К., Бурков В.Н., Вилкова Н.Н., Рапацкая С.Т. Модели и механизмы внутрифирменного управления. М., Институт проблем управления, 1994.
7. Ковалев В.В. Финансовый анализ. М., Финансы и статистика, 1998.
8. Емельянов С.В., Бурков В.Н., Ивановский А.Г., Немцева А.Н., Ситников В.И., Соколов В.И., Щепкин А.В. Метод деловых игр. Международный центр научно-технической информации, М. 1976.
9. Чепрунова О.Ю. Щепкин А.В. Разработка экспериментов с моделями организационных систем. Автоматика и телемеханика, 1988, N 8.
10.Опойцев В.И. Равновесие и устойчивость в моделях коллективного поведения. М., Наука, 1977.
11. Управленческий учет: Учебное пособие/под редакцией А.Д. Шеремета. - М: ИД ФБК-ПРЕСС, 2000.
12. Баркалов С.А., Бурков В.Н., Глухов А.В., Курочка Н.Н., Мещерякова О.К., Серебряков В.И. Диагностика, оценка и реструктуризация строительного предприятия. Бизнес-планирование. Воронежская государственная архитектурностроительная академия, Воронеж, 2000.
13. Бурков В.Н., Данев Б., Еналеев А.К., Кондратьев В.В., На-нева Т.Б., Щепкин А.В. Большие системы: моделирование организационных механизмов. М.: Наука, 1989.
14. Бурков В.Н., Кашенков А.Р. Противозатратные механизмы
управления научными исследованиями и разработками. В кн. Совершенствование организационно-экономического механизма управления деятельностью научно
исследовательских и проектно-конструкторских учреждений. М.: МДНТП, 1988.
15. Бурков В.Н., Кашенков А.Р. Принципы построения противозатратных механизмов прогрессивного налогообложения для двух моделей хозрасчета в науке. М.: МДНТП, 1988.
16. Волгин Н.А. Современные модели оплаты труда: методика и рекомендации по внедрению. М.: ИНПИОН. 1992.
17. Дудашова В.П. Мотивация труда в менеджменте. Кострома. КГТУ, 1996.
18. Мироносецкий Н.Б., Исаева Н.А., Парфенова Л.К., Щеглов Ю.А. Планирование и анализ хозяйственной деятельности предприятия в условиях налоговой системы. Новосибирский государственный университет, 1991.
19. Динова Н.И. Бригадные формы оплаты труда. - В кн. Механизмы управления социально-экономическими системами. М. Институт проблем управления, 1988.
20. Щепкин А.В. Имитационная игра Бригадные формы оплаты труда. В кн. Modemizace vyucovaciho procesu na vysokych skolach a pri vychove a vzdelavani dospelych, Praha, 1986.
Содержание раздела




