ПРИНЦИП РАВНЫХ РЕНТАБЕЛЬНОСТЕЙ
Таким образом, рассмотренный механизм распределения однотипных работ и прибыли явно не эффективен.
Не меняя механизма распределения объемов работ, внесем коррективы в механизм распределения прибыли. Введем для этого внутреннюю цену, обозначив ее через 1. Внутреннюю цену будем определять по формуле
і=і
Тогда внутренняя или условная прибыль i-го подразделения может быть представлена в виде
1 xi
ji = 1xi -т .
2 Г
А реальная прибыль этого подразделения будет определяться
как
p i П.
i n
Е jj
j=i
Ниже приведены результаты игрового эксперимента по использованию внутренней цены при распределении прибыли фирмы. Эксперимент проводился не с автоматами, а с реальными игроками.
В игре участвовало шесть игроков, все значения параметров игры такие же, как и в предыдущем эксперименте.
Эксперимент с реальными игроками занимает существенно больше времени. Это касается как времени проведения одной партии игры, так и времени проведения всего игрового эксперимента, так как скорость сходимости в равновесную ситуацию, если она существует, в экспериментах, проводимых с реальными игроками, как правило, ниже, чем в играх с автоматами. Кроме того, большое количество времени занимает у игроков процесс обработки информации, принятия решения и передачи этого решения руководителю игры. Эти причины не всегда позволяют организаторам игровых экспериментов провести достаточно партий игры. Поэтому здесь результаты проведения эксперимента представлены на таблице 1, в которой отражено развитие ситуации в первых десяти партиях.
| Таблица 1. |
| Партия 1 |
Номер игрока |
1 |
2 |
3 |
4 |
5 |
6 |
| Заявленный объем работ |
20,00 |
22,00 |
25,00 |
33,00 |
30,00 |
18,00 |
| Полученный объем работ |
27,03 |
29,73 |
33,78 |
44,59 |
40,54 |
24,32 |
| Внутренняя цена |
6,08 |
| Условная прибыль |
91,31 |
92,40 |
110,3 |
105,4 |
129,1 |
105,6 |
| Прибыль фирмы |
318,08 |
| Прибыль |
45,79 |
46,34 |
55,33 |
52,88 |
64,76 |
52,98 |
(N
%
к |
Заявленный объем работ |
28,00 |
25,00 |
27,00 |
35,00 |
37,00 |
40,00 |
| Полученный объем работ |
29,17 |
26,04 |
28,13 |
36,46 |
38,54 |
41,67 |
| Внутренняя цена |
4,69 |
| Условная прибыль |
51,65 |
54,25 |
65,92 |
60,13 |
74,56 |
71,30 |
d
с |
Прибыль фирмы |
340,32 |
| Прибыль |
46,52 |
48,87 |
59,38 |
54,16 |
67,16 |
64,23 |
со
%
к |
Заявленный объем работ |
30,00 |
26,00 |
31,00 |
38,00 |
40,00 |
45,00 |
| Полученный объем работ |
28,57 |
24,76 |
29,52 |
36,19 |
38,10 |
42,86 |
| Внутренняя цена |
4,29 |
| Условная прибыль |
40,82 |
44,81 |
53,89 |
45,96 |
59,60 |
52,48 |
d
с |
Прибыль фирмы |
340,41 |
| Прибыль |
46,70 |
51,26 |
61,65 |
52,58 |
68,19 |
60,04 |
%
К |
Заявленный объем работ |
32,00 |
28,00 |
36,00 |
29,00 |
43,00 |
40,00 |
| Полученный объем работ |
30,77 |
26,92 |
34,62 |
27,88 |
41,35 |
38,46 |
| Внутренняя цена |
4,33 |
| Условная прибыль |
38,46 |
44,01 |
49,93 |
55,86 |
56,79 |
60,76 |
d
с |
Прибыль фирмы |
340,42 |
| Прибыль |
42,82 |
48,99 |
55,58 |
62,18 |
63,22 |
67,63 |
*п
%
К
н
Рч |
Заявленный объем работ |
27,00 |
25,00 |
29,00 |
27,00 |
41,00 |
34,00 |
| Полученный объем работ |
29,51 |
27,32 |
31,69 |
29,51 |
44,81 |
37,16 |
| Внутренняя цена |
4,92 |
| Условная прибыль |
58,05 |
59,72 |
72,16 |
72,56 |
76,95 |
84,12 |
03
С |
Прибыль фирмы |
339,96 |
| Прибыль |
46,59 |
47,93 |
57,92 |
58,24 |
61,77 |
67,52 |
|
| Партия 6 I |
Номер игрока |
1 |
2 |
3 |
4 |
5 |
6 |
| Заявленный объем работ |
23,0 |
27,0 |
26,0 |
29,0 |
42,0 |
35,0 |
| Полученный объем работ |
25,2 |
29,6 |
28,5 |
31,8 |
46,1 |
38,4 |
| Внутренняя цена |
4,95 |
| Условная прибыль |
61,1 |
58,6 |
73,2 |
72,9 |
76,0 |
84,5 |
| Прибыль фирмы |
337,61 |
| Прибыль |
48,3 |
46,4 |
57,9 |
57,7 |
60,2 |
66,8 |
| Партия 7 |
Заявленный объем работ |
21,0 |
22,0 |
25,0 |
26,0 |
36,0 |
33,0 |
| Полученный объем работ |
25,7 |
26,9 |
30,6 |
31,9 |
44,1 |
40,4 |
| Внутренняя цена |
5,52 |
| Условная прибыль |
75,8 |
76,1 |
90,9 |
91,3 |
104, |
106, |
| Прибыль фирмы |
3411 |
,04 |
| Прибыль |
47,4 |
47,6 |
56,8 |
57,1 |
65,3 |
66,5 |
| Партия 8 |
Заявленный объем работ |
22,0 |
23,0 |
27,0 |
28,0 |
33,0 |
34,0 |
| Полученный объем работ |
26,3 |
27,5 |
32,3 |
33,5 |
39,5 |
40,7 |
| Внутренняя цена |
5,39 |
| Условная прибыль |
72,5 |
72,5 |
87,1 |
87,0 |
101, |
101, |
| Прибыль фирмы |
34-3,88 |
| Прибыль |
47,8 |
47,8 |
57,4 |
57,3 |
66,8 |
66,5 |
| Партия 9 |
Заявленный объем работ |
23,0 |
24,0 |
26,0 |
28,0 |
30,0 |
32,0 |
| Полученный объем работ |
28,2 |
29,4 |
31,9 |
34,3 |
36,8 |
39,2 |
| Внутренняя цена |
5,52 |
| Условная прибыль |
76,1 |
75,8 |
91,3 |
91,3 |
106, |
106, |
| Прибыль фирмы |
34-3,57 |
| Прибыль |
47,7 |
47,5 |
57,2 |
57,2 |
66,7 |
66,9 |
| I Партия 10 |
Заявленный объем работ |
22,5 |
22,0 |
27,0 |
27,0 |
31,0 |
31,5 |
| Полученный объем работ |
27,9 |
27,3 |
33,5 |
33,5 |
38,5 |
39,1 |
| Внутренняя цена |
5,59 |
| Условная прибыль |
78,1 |
78,0 |
93,7 |
93,7 |
109, |
109, |
| Прибыль фирмы |
34-4,40 |
| Прибыль |
47,8 47,8 57,4 57,4 66,9 66,9 |
Таким образом, в ситуации равновесия игроки сообщают заявки, обеспечивающие им получение максимальной прибыли. В свою очередь, прибыль, полученная фирмой при введении механизма внутренних цен, в ситуации равновесия более чем на 90% выше прибыли, полученной до введения механизма внутренних цен.
ПРИНЦИП РАВНЫХ РЕНТАБЕЛЬНОСТЕЙ
Предыдущий раздел был посвящен вопросам распределения работ между подразделениями фирмы при отсутствии единой технологической цепочки, то есть каждое подразделение фирмы могло выполнить любую работу по договору. Ситуация меняется, если каждое подразделение может выполнять только свой вид работы. Таким образом, работы по подразделениям фирмы распределять уже не надо. Однако необходимо определить объем финансирования для каждого подразделения. Как это сделать?
Пусть зг-затраты на выполнение работ i-м подразделением
П
фирмы таковы, что Е зі C , то есть работа для фирмы в принципу
пе выгодна. Необходимо определить сг-объем финансирования выполнения работ в каждом подразделении фирмы i=l,
Один из вариантов решения этой проблемы - это использовать принцип равных рентабельностей [6]. Рентабельность определяется как прибыль на 1 руб. затрат.
Максимальная рентабельность всего договора на уровне всей
фирмы ртах
Соответственно, рентабельность i-го подраз
деления фирмы pi =
-L . Если ставится задача обеспечить
равную рентабельность во всех подразделениях фирмы, то для определения объемов финансирования каждого подразделения на основе принципа равных рентабельностей можно записать
- Зі _, - 3j i=l
Из первого уравнения этой системы, получаем
cj - 3j = 3j - 3j
з
или
CJ= 3 J ¦
3,¦
Из последнего уравнения системы получаем
n г П
U f Е 3, = С.
J=1 3 J=1
И, наконец,
c = jC ¦
13,
7=1
Так как руководству фирмы не известны точные значения з, при определении объемов финансирования центр использует информацию, полученную от подразделений фирмы sh i=1, ...,n. Тогда
s, С Ci = лС ¦
Е s
=1
Прибыль i-го подразделения фирмы может быть записана как
s, n
Esj
=1
Легко видеть, что для увеличения прибыли каждому подразделению выгодно завышать оценку sДля устранения этой тенденции введем дополнительные отчисления от сверхплановой прибыли, которые равны (s-3) В этом случае остаточную прибыль можно представить в виде
Пі = C - 3 - a(si - 3i) = С - 3i - a(si - 3), (5)
Els,
=1
где a-норматив дополнительных отчислений от сверхплановой прибыла
Ситуация равновесия по Нэшу находится из условия
(6)
П
ds,
или
n С a n Y
s, = У s, 1--У s,
j =1 V C J=1
Складывая эти n уравнений, получаем n C n -1
У sj =---
j=j a n
Таким образом,
s=
Выражение (6) определяет равновесие по Нэшу, если s, з,. Подразделению фирмы не выгодно будет завышать свои затраты, если с ростом заявляемых затрат будет снижаться прибыль подразделения, то есть, если выполняется условие
дП, ds,
Из этого условия следует
У sj - s,
1 _ J=1
C-a0
У.*,
\j=1 0
или
У
j=1
С n Y
іл
vJ=1
Вычитая из обеих частей последнего неравенства по 1, получим
Но
С -E sj
С-Е s,
j=i
Г n ^
E s
Vj=1 ' 0
(7)
-j-1 = р - рентабельность работ, определяемая на
j=1
этапе планирования. Потому выражение (7) можно переписать в виде
(р +1 - a)
Е Sj
j=1
Вычитая еще раз по 1 из обеих частей этого неравенства, получим
Zs,
(р +1 - a) р +1
или
¦ (р+7 Es/
j =1
Умножим обе части последнего неравенства на Си вычтем из обеих частей по 1. После несложных преобразований получим
р +1 - a
(Р +1)2
С.
(8)
Пусть a=1, то есть у подразделения фирмы изымается вся сверхплановая прибыль. Тогда при ртах1 неравенство (8) будет выполняться всегда, если справедливо неравенство
з Р max Jmin / \2
(Р max + 1)
(9)
Рассмотрим случай, когда з1=з2=...=зп=з. При этом (9) представим в виде
(рmax + C
Pm
Умножая это неравенство на 1/п и учитывая, что
-= Рmax + 1, полУчаем
пз
Р max + 1
пр max
(10)
или
1
Р ?-
max
п -1
(11)
Таким образом, только для низкорентабельных договоров можно надеяться на то, что принцип равных рентабельностей обеспечит достоверность оценок затрат, сообщаемых подразделениями фирмы.
Рассмотрим теперь случай когда a1, то есть у подразделений фирмы не только отбирается сверхплановая прибыль, но подразделения еще и штрафуются за завышение оценок затрат.
Предположим, что о=1+8, где 80, тогда (8) можно переписать в виде
Р - S (Р+1)2
C,
и для случая, когда на фирме п одинаковых подразделений неравенство (10) записывается как
Р max + 1
п(Рmax - d )
или
1 + 5п
Р ?-
max
п -1
А отсюда следует, что ограничение на максимальную рентабельность становится менее жестким.
Действительно, если n=11 и о=1, то максимальная рентабельность, при которой еще может быть обеспечено получение достоверной информации, равна 10%. В то же время для случая, когда 0=1,1, то есть штраф составляет 10% от превышения оценки затрат над фактическими затратами, максимальная рентабельность, обеспечивающая получение достоверной информации, уже равна 21 %.
Ниже приводятся результаты игрового эксперимента с шестью автоматами. Условия эксперимента следующие: C=900; n=6; зі=100; з2=110; з3=120; з4=130; з5=140; з6=150; 0=1; у]=0,3;
у2=0,5; у3=0,4; у4=0,6; у5=0,5; у6=0,7. Легко посчитать, что Ртах=0,2. А проведенный выше анализ показал, что в рассматриваемом случае достоверность информации может обеспечиваться при 0=1, ртах 0,2 одинаковых затратах подразделений на выполнение работ.
Из (5) нетрудно определить положение цели i-го автомата. В k-й партии оно определяется выражением
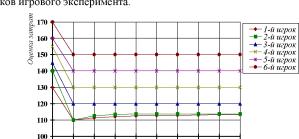
Из графика следует, что третий, четвертый, пятый и шестой игроки сообщают достоверную информацию, а первый и второй завышают свои затраты.
На рис. 14 представлен график изменения стратегий автоматов, когда a=1,04.
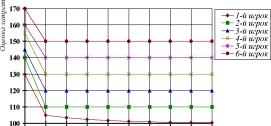
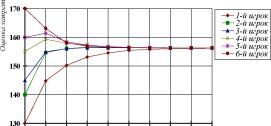
ПРОТИВОЗАТРАТНЫЕ МЕХАНИЗМЫ УПРАВЛЕНИЯ
Рассмотрим пути построения противозатратного механизма. Основная идея, которая закладывается в этот принцип, заключается в следующем. При уменьшении затрат на производство и росте потребительских свойств, прибыль должна увеличиваться [13-15]. Так как П=рЗ, то отсюда следует необходимость поставить рентабельность в зависимость от затрат З и эффекта L таким образом, чтобы р увеличивалось при уменьшении З и увеличении L. Для этого вводится новый показатель
L
~З
и предполагается что р=р(Э). Показатель Э характеризует эффективность продукта (фактически это эффект у потребителя на 1 руб. затрат у производителя). Для того чтобы механизм формирования цены (стоимости) продукта был бы противозатратным, необходимо, чтобы выполнялись следующие требования:
- прибыль П=р(Э)З была убывающей функцией затрат;
- стоимость производства С=[1+р(Э)]З должна быть возрастающей функцией затрат.
Из первого требования получаем
dL = А [р (э )х З ]=р (э )-э А о,
йЗ йЗ^У ' J ? ' йЭ
а из второго требования имеем
d_
АЗ
([і+р (Э)]х З )=і+р (э )-э Аэ
Оба эти неравенства можно записать в следующем виде:
р (Э ) 1.
о Э А йЭ
э а
йЭ
р (Э) через к(Э), то-
В соответствии с [13] обозначим
гда последнее неравенство можно записать в форме дифференциального уравнения
3d- - р(Э)= h(3), (12)
аЭ
где h(3) произвольная функция, принимающая значения в интервале (0,1). Это уравнение легко решается. Действительно, для этого сделаем замены
Ф )=3 р (э)
р (3) = Эи(3)
dp
. Оз
du
d3
и( Э) + Э
Подставляя эти выражения в (12) получаем
du h( Э)
d5 ~ ~э2~ .
А это уравнение легко интегрируется
„(Э) = ЭIhdx.
1 Х
При интегрировании используется условие, что р(1)=0. Содержательно это означает, что продукт, для которого эффект равен затратам, не дает прибыли. Таким образом, общий вид зависимости р(3), обеспечивающий противозатратность по прибыли механизма формирования цены (стоимости) представляется как
р (э )=э jЩ^Ох.
1 х
Для иллюстрации этого подхода рассмотрим следующий пример. Пусть h(3)=k, 0k1. В этом простейшем случае имеем
3 k
р (Э ) = 3 j ~d = k (Э-1).
1Х
Стоимость производства тогда будет определяться выражением С=[1+р(Э)]З=ЗЩ1-З)={1-ЩЗ+kL.
То есть стоимость продукта является линейной комбинацией затрат на производство и эффекта.
Идея применения линейной комбинации между минимально необходимыми затратами и максимально возможной оценкой работы будет в дальнейшем использована при разработке процедуры, предназначенной для определения объемов финансирования подразделений фирмы.
Рассмотрим теперь следующий механизм.
Предварительно для всех подразделений устанавливается единый минимальный норматив рентабельности р0 (при меньшей рентабельности выполнение работ становится невыгодным для всей фирмы). То есть
С-Ъ
Ро,
i=1
После этого со всех подразделений фирмы собираются оценки затрат на выполнение работ sr, i=1, После сбора информации о затратах для каждого подразделения руководство фирмы устанавливает лимитную (максимальную) стоимость работ (максимальный объем финансирования)
Li = С-(1 + р0) Ъsj -si
=1
Главной особенностью лимитной стоимости работ i-го подразделения является тот факт, что она не зависит от величины оценки затрат самого этого подразделения.
На основе лимитной стоимости работ определяется лимитная рентабельность работ подразделения
hr
Li - sr
si
Зная минимальный р0 и максимальный h уровни рентабельности, руководство фирмы определяет договорной уровень рентабельности
Pr=(1-k)po+khi, ke(0;1). (13)
То есть, договорной уровень рентабельности pr является линейной комбинацией между минимальным р0 и максимальным hi уровнями рентабельности.
На основе рассчитанного уровня рентабельности определяется объем финансирования
c1=(1+p1)s1. (14)
В этом случае выражение для прибыли i-го подразделения фирмы может быть представлено в виде
ni=Ci-3i-a(Si-3i)=(1+pi)Si-3i-a(Si-3;). (15)
Или
П=[(1-k)(1+po)-a]s i+kLi-(1-a)3i.
Отсюда следует, что подразделениям фирмы невыгодно будет завышать оценки затрат на выполнение работ, если
1-a+(1-k)p0rk0.
Это неравенство можно переписать в виде
k 1--a . (16)
1 + po
С другой стороны, объем финансирования подразделения фирмы с ростом его затрат должен расти. Для того, чтобы выяснить условия выполнения этого требования запишем
Cl=(1+Pl)Sl=[1+(1-k)pork]Sl+kLl=(1-k)(1 +po)Si+kLi.
Отсюда следует
(1-k)(1+po)0
или k1.
n
Для реализуемости механизма необходимо, чтобы Z ci C .
i=1
Действительно, так как
Z Ci =(1 - kn)j + po )Z si + knC, (17)
i=1 i=1
то из неравенства
(1 - kn)1 + po )Z si + knC C
i=1
следует, что
(1- kn) C -(1 + po )Z'
i=1
Или
(18)
Заметим здесь, что при формировании объемов финансирования на основе рассматриваемого механизма не все финансовые средства C распределяются между подразделениями фирмы, так
П
как Z c ? C , в то же время при использовании принципа равных
i=1
рентабельностей на финансирование подразделений расходовалась вся сумма средств C.
Покажем теперь, что договорная рентабельность каждого подразделения будет не ниже нормативной.
Для этого достаточно показать, что hi-Po- Действительно
C -(l + Po )| Z Sj - si
C -(l + Po )Z sj
j=1
+ Po Po ,
hi =
s.
или
C -(l + Po)Z Sj
-j^ 0.
si
Это неравенство справедливо, так как C - (l + P0 )Z si 0 .
i=i
Таким образом, при выполнении условий (16) и (18) подразделениям фирмы не выгодно будет завышать оценки своих собственных затрат. Прибыль каждого подразделения в этом случае зависит только от фактических затрат и может быть записана в виде
Пі=[(1-k)Pa-k]3l+kLl =Po3i+k
C -(l + P o )Z 3 j j=i
На рис. 16 изображены две прямые
a
1 + Po
Точки, находящиеся в заштрихованной области на графике удовлетворяют неравенствам (16) и (18). Поэтому эту область можно считать областью противозатратности. Отсюда следует, чтобы область противозатратности была не пуста, должно выполняться условие
1 Ро
п 1 + Ро
или
Ро -П - (19)
п -1
Другими словами, если k, п, а и р0 таковы, что эта область не пуста, то подразделениям выгодно сообщать руководству фирмы истинные значения затрат на выполнение работ.
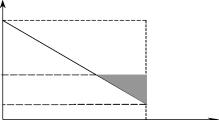
k
1
1 п
Р о
р о + 1
0 1 а
Рис. 16.
Заметим здесь, что последнее неравенство - это ограничение на минимальную рентабельность, в то время как при распределении финансовых средств на основе принципа равных рентабельностей выражение (11) - это ограничение на максимальную рентабельность. Нетрудно также заметить, что с ростом п область противозатратности сокращается.
Для иллюстрации действия рассматриваемого механизма распределения финансовых средств рассмотрим результаты проведенного игрового эксперимента (Таблица 2). Условия эксперимента следующие: C=1000; n=6; з1=100; з2=100; з3=110; з4=110; з5=120; з6=120; р0=0,15; k=0,16; a=0,97.
| Таблица 2 |
| Партия 1 |
Номер игрока |
1 |
2 |
3 |
4 |
5 |
6 |
| Оценка затрат |
120 |
125 |
130 |
145 |
150 |
165 |
| Лимитная стоимость |
177,7 |
183,5 |
189,2 |
206,5 |
212,2 |
229,5 |
| Лимитная рентабельность |
0,481 |
0,468 |
0,456 |
0,424 |
0,42 |
0,39 |
| Фактическая рентабельность |
0,203 |
0,201 |
0,199 |
0,194 |
0,19 |
0,19 |
| Объем финансирования |
144,3 |
150,1 |
155,8 |
173,1 |
178,8 |
196,1 |
| Прибыль |
24,96 |
25,86 |
26,16 |
29,16 |
29,76 |
32,46 |
| Прибыль фирмы |
168,66 |
| Партия 2 |
Оценка, затрат |
110 |
130 |
130 |
140 |
140 |
150 |
| Лимитная стоимость |
206,5 |
229,5 |
229,5 |
241,0 |
241,0 |
252,5 |
| Лимитная рентабельность |
0,877 |
0,765 |
0,765 |
0,721 |
0,72 |
0,68 |
| Фактическая рентабельность |
0,266 |
0,248 |
0,248 |
0,241 |
0,24 |
0,24 |
| Объем финансирования |
139,3 |
162,3 |
162,3 |
173,8 |
173,8 |
185,3 |
| Прибыль |
29,60 |
33,20 |
32,90 |
34,70 |
34,40 |
36,20 |
| Прибыль фирмы |
201,00 |
| Партия 3 |
Оценка, затрат |
100 |
140 |
135 |
150 |
130 |
130 |
| Лимитная стоимость |
212,2 |
258,2 |
252,5 |
269,7 |
246,7 |
246,7 |
| Лимитная рентабельность |
1,123 |
0,845 |
0,870 |
0,798 |
0,90 |
0,90 |
| Фактическая рентабельность |
0,306 |
0,261 |
0,265 |
0,254 |
0,27 |
0,27 |
| Объем финансирования |
130,5 |
176,5 |
170,8 |
188,0 |
165,0 |
165,0 |
| Прибыль |
30,56 |
37,76 |
36,56 |
39,26 |
35,36 |
35,36 |
| Прибыль фирмы |
214,86 |
| Партия 4 |
Оценка, затрат |
100 |
150 |
140 |
170 |
140 |
150 |
| Лимитная стоимость |
137,5 |
195,0 |
183,5 |
218,0 |
183,5 |
195,0 |
| Лимитная рентабельность |
0,375 |
0,300 |
0,311 |
0,282 |
0,31 |
0,30 |
| Фактическая рентабельность |
0,186 |
0,174 |
0,176 |
0,171 |
0,18 |
0,17 |
| Объем финансирования |
118,6 |
176,1 |
164,6 |
199,1 |
164,6 |
176,1 |
| Прибыль |
18,60 |
27,60 |
25,50 |
30,90 |
25,20 |
27,00 |
| Прибыль фирмы |
154,80 |
| Партия 5 |
Оценка, затрат |
110 |
140 |
120 |
145 |
130 |
135 |
| Лимитная стоимость |
229,5 |
264,0 |
241,0 |
269,7 |
252,5 |
258,2 |
| Лимитная рентабельность |
1,086 |
0,886 |
1,008 |
0,860 |
0,94 |
0,91 |
| Фактическая рентабельность |
0,300 |
0,268 |
0,287 |
0,264 |
0,28 |
0,27 |
| Объем финансирования |
142,9 |
177,4 |
154,4 |
183,2 |
165,9 |
171,7 |
| Прибыль |
33,28 |
38,68 |
00
г-
-t |
39,28 |
36,28 |
37,18 |
| Прибыль фирмы |
219,48 |
|
| Партия 6 |
Номер игрока |
1 |
2 |
3 |
4 |
5 |
6 |
| Оценка затрат |
100 |
100 |
110 |
110 |
120 |
120 |
| Лимитная стоимость |
356, |
356, |
367, |
367, |
379, |
379, |
| Лимитная рентабель- |
2,56 |
2,56 |
2,34 |
2,34 |
2,16 |
2,16 |
| Фактическая рентабель- |
0,53 |
0,53 |
0,50 |
0,50 |
0,47 |
0,47 |
| Объем финансирования |
153, |
153, |
165, |
165, |
176, |
176, |
| Прибыль |
53,5 |
53,5 |
55,0 |
55,0 |
56,5 |
56,5 |
| Прибыль фирмы |
330,36 |
| Партия 7 |
Оценка, затрат |
110 |
100 |
110 |
110 |
120 |
120 |
| Лимитная стоимость |
356, |
344, |
356, |
356, |
367, |
367, |
| Лимитная рентабель- |
2,23 |
2,44 |
2,23 |
2,23 |
2,06 |
2,06 |
| Фактическая рентабель- |
0,48 |
0,51 |
0,48 |
0,48 |
0,46 |
0,46 |
| Объем финансирования |
163, |
151, |
163, |
163, |
174, |
174, |
| Прибыль |
53,5 |
517 |
53,2 |
53,2 |
54,7 |
54,7 |
| Прибыль фирмы |
321 |
,12 |
| Партия 8 |
Оценка, затрат |
100 |
100 |
130 |
110 |
120 |
120 |
| Лимитная стоимость |
333, |
333, |
367, |
344, |
356, |
356, |
| Лимитная рентабель- |
2,33 |
2,33 |
1,82 |
2,13 |
1,97 |
1,97 |
| Фактическая рентабель- |
0,49 |
0,49 |
0,41 |
0,46 |
0,44 |
0,44 |
| Объем финансирования |
149, |
149, |
184, |
161, |
172, |
172, |
| Прибыль |
49,8 |
49,8 |
54,9 |
51,3 |
52,8 |
52,8 |
| Прибыль фирмы |
311 |
,88 |
| I Партия 9 |
Оценка, затрат |
100 |
100 |
110 |
110 |
120 |
120 |
| Лимитная стоимость |
356, |
356, |
367, |
367, |
379, |
379, |
| Лимитная рентабель- |
2,56 |
2,56 |
2,34 |
2,34 |
2,16 |
2,16 |
| Фактическая рентабель- |
0,53 |
0,53 |
0,50 |
0,50 |
0,47 |
0,47 |
| Объем финансирования |
153, |
153, |
165, |
165, |
176, |
176, |
| Прибыль |
53,5 |
53,5 |
55,0 |
55,0 |
56,5 |
56,5 |
| Прибыль фирмы |
330,36 |
Отсюда следует, что наилучшие результаты достигаются в том случае, когда подразделения фирмы сообщают достоверную информацию. В то же время искажение информации приводит к уменьшению прибыли подразделений и фирмы в целом.
ПРОТИВОЗАТРАТНОСТЬ ПРИ ФОРМИРОВАНИИ ФОНДА ОПЛАТЫ ТРУДА
Эффективность работы подразделений фирмы зависит не только от эффективности работы сотрудников (их квалификации, заинтересованности в снижении затрат и т.д.), но и от объективных условий, связанных с видом выполняемых работ.
До сих пор эффективность работы подразделения определялось показателем рентабельности, зависящим от стоимости договора и затрат подразделения. Разные подразделения объективно имеют разные соотношения между стоимостью живого труда и стоимостью материальных затрат или привлеченного труда, что ставит их в неравные условия [6].
Действительно, пусть зі=Аі+Ві, где Агстоимость живого труда, Вгстоимость материальных затрат или привлеченного труда, тогда
C-(l + Р о )Х 3 j j=1
Пі=ро(Аі+Ві)+к
и ФОТ i-го подразделения можно представить в виде
ФОТг=Аг+цПг,
где /I - процент отчисления в ФОТ от прибыли, или
ФОТ1=(1+рро)А1+троВ,+тк
C -(l + Ро )Х 3j j=i
Если А1=А2и В1В2, то не трудно видеть, что ФОТ1ФОТ2. Одинаковые условия при формировании ФОТ подразделений фирмы обеспечиваются, если при определении объема финансирования используется следующая процедура.
Для всех подразделений устанавливается единый минимальный норматив рентабельности ро
Со всех подразделений фирмы собираются заявки затрат на выполнение работ:
аг-оценка стоимости живого труда;
6г-оценка стоимости материальных затрат или привлеченного труда.
После сбора информации о затратах для каждого подразделения руководство фирмы определяет минимальный объем финансирования
Wi=(1+po)ai+bi.
Затем определяется лимитная (максимальная) стоимость работ i-го подразделения фирмы
п п_
Zw-wi = C-(1+po) Zaj-ai
Z bj - bi
Vj=1 0
L, = C -
.(20)
На основе лимитной стоимости работ определяется лимитная рентабельность работ подразделения
f n \ n n
C-po Zaj-ai -Zaj-Zbj
\j=1 0 j=1 j=1
Li - ai - bi
(21)
hi
a,
a,
Затем руководство фирмы определяет договорной уровень рентабельности в соответствии с выражением (13)
kC + Pofli - kpo Z aj - k Z aj + Z bj
Pi
a,
На основе рассчитанного уровня рентабельности определяется объем финансирования
Теперь можно определить прибыль i-го подразделения фирмы Пі=Сі-Аі-Ві- a(arAi)-p(brBi).
или
Из последнего выражения следует, что подразделениям фирмы невыгодно будет завышать оценки затрат живого труда на выполнение работ, если выполняются условия (16) и затрат привлеченного труда, если
1-k-bo.
Объем финансирования подразделения фирмы с ростом затрат как живого, так и привлеченного труда должен расти. Из выражения (22) следует (1-k)0 или k1.
Нетрудно проверить, что для реализуемости рассматриваемого механизма должно выполняться неравенство (19).
Содержание раздела




