Коалиционная неманипулируемость прямых механизмов
Возьмем, например, такой профиль предпочтений, что функции полезности jj (xj) = -|Xj |, j2 (x2) = x2 -1/2 имеют точки пика равные
соответственно (0, 1/2). Сообщая достоверную информацию, элементы получают планы (1, 1/2) и полезности (1, 0) соответственно.
Если же первый активный элемент сообщит недостоверную информацию: 1/2, а второй сохранит своё сообщение 1/2, то будут назначены планы (12,12) и полезности элементов в этом случае будут (0, 0).
Таким образом, в настоящем разделе сформулированы достаточные условия неманипулируемости прямых механизмов планирования, накладывающие ограничения на структуру множеств диктаторства (Т.2.1.1). Кроме этого, исследование манипулируемости механизмов планирования в АС с двумя АЭ (примеры 2.1.1, 2.1.2) дает наглядную геометрическую интерпретацию условий неманипулируемости в терминах множеств диктаторства.
§2. Коалиционная неманипулируемость прямых механизмов
В §1 настоящей главы были построены достаточные условия неманипулируемости прямых механизмов планирования. В настоящем параграфе мы введем понятие коалиционной неманипулируемости и получим необходимые и достаточные условия коалиционной неманипулируемости для механизмов, удовлетворяющих предположению А.2.1.1.
Введем несколько отношений между векторами в Rn, которые будут необходимы нам в дальнейшем. Будем писать, что x р у,
X, у 6 Rn если хс(р) = Ус(ру xA(р) Уа(р ХМ(р) Ум(р) . Используя это
обозначение, определение множеств Бр, Dp можно записать следующим
образом:
Бр = 6 Rn| ~ р h(~)}, р 6pn .
DP = {~ 6 Rn| ~с(р) 6 Projc(р) Бр, ~ р хр (~с(р))}, р 6РП
Кроме отношения р определим отношение р . Будем записывать х р у , если хс(р) = Ус(р XA(р) ? Уа(ру хм(р) ^ Ум(р).
Для каждого подмножества активных элементов J с I и для каждого вектора состояний р 6pn определим множества D(р, J) и вектора состояний с(р, J) следующим образом:
D(р, J) = {~ 6 Rn\ ~с(р) 6 Рго.Іс(р)Бр , ~ = хр (~с(р)Х ~_J р xPj (~с(р))} ,
с(р, J) 6pn : cJ (р, J) = рі1 и i 61 \ J ® с (р, J) ='с'.
В дальнейшем будем исследовать прямые механизмы, удовлетворяющие следующему условию
A.2.2.1. р 6pn, J 61 ® D(р, J) с D(р, j).
Условие А.2.2.1 содержательно означает, что при переходе из множества диктаторства Dp, р 6pn с меньшим числом диктаторов в
множество Dc( J) с большим количеством диктаторов, АЭ не являвшиеся диктаторами в Dp получат планы, не лучшие прежних.
Будем говорить, что прямой механизм h: Rn ® Rn коалиционно
манипулируем, если $r е Rn, $J с 1, 3rJ е RJ такие, что j е J ®
® j j (hj (rJ, r- J)) ^ j j (hj (rJ, r- J)) и $г e J ® ji (hi (~J, r- j )) 9г (hi (rj, r- j )) - Содержательно, это означает, что при некотором профиле предпочтений найдется коалиция элементов, каждый элемент которой не проигрывает от сообщения недостоверной информации и найдется элемент, который строго выигрывает.
Следует отметить, что такое определение коалиционной неманипулируемости расходится с общепринятым [22,108]
Определение 2.2.1. Коалиционно неманипулируемым назовем
механизм h: Rn ® Rn такой, что r е Rn, J с I, J е RJ ®
{i е J ® ji (hi (rJ, r-j )) ji (hi (rj, r-j ))} или (3j e J:
j j (hj (~J, r- J)) j j (hj (rJ, r- J))}.
Коалиционная неманипулируемость означает, что для любого профиля предпочтений и для любой коалиции ни какая коалиция АЭ не может получить выигрыш от создания коалиции либо полезность одиного из АЭ рассматриваемой коалиции строго убывает при образовании коалиции.
Верны следующие утверждения
Лемма 2.2.1. Пусть механизм h: Rn ® Rn удовлетворяет
предположениям А.2.1.1, А.2.2.1 и для него D = D0, тогда этот механизм коалиционно неманипулируем. ^
Лемма 2.2.2. Пусть механизм h: Rn ® Rn удовлетворяет А.2.1.1 и коалиционно неманипулируем, тогда D = D0. ^
Лемма 2.2.3. Пусть механизм h: Rn ® Rn удовлетворяет А.2.1.1 и коалиционно неманипулируем, тогда выполнено А.2.2.1. ^
Следствием Л.2.2.1-Л.2.2.3 является следующая теорема.
Теорема 2.2.1. Для того, чтобы прямой механизм h: Rn ® Rn удовлетворяющий А.2.1.1, был коалиционно неманипулируем необходимо и достаточно, чтобы выполнялись условия А.2.2.1 и D = D0 . ^
Теорема 2.2.1 дает необходимые и достаточные условия для коалиционной неманипулируемости прямых механизмов в смысле определения 2.2.1.
В следующем параграфе мы рассмотрим обобщения результатов § 1 настоящей главы на механизмы планирования с векторными планами,
что является обобщением результатов работ [7,14] о неманипулируемости механизмов голосования.
§3. Неманипулируемость прямых механизмов планирования с векторными планами
В §§ 1-2 настоящей главы мы получили достаточные условия неманипулируемости и необходимые и достаточные условия коалиционной неманипулируемости в терминах множеств диктаторства. Эти результаты включают результаты работ [7,14,53] для механизмов планирования со скалярными планами как частные случаи.
В настоящем параграфе мы обобщим результаты этих работ на механизмы планирования с векторными планами.
Рассмотрим активную систему с сообщением информации. Обозначим множество активных элементов через I. Пусть активным
элементам назначаются векторные планы х1 е RJi, где J - множество компонент планов для i -го активного элемента. Обозначим через J множество всех компонент планов всех активных элементов J = - J1 .
іеі
Будем считать, что функции полезности р1 (xi) активных элементов являются однопиковыми, т.е. такими, что для каждого активного элемента і е I существует единственная точка Г е RJi такая, что для любой точки х1 е RJi такой, что х1 Ф Г выполняется р1 (х1) (р1 (Ах1 + (1 -А)r1) р1 (r1), А е (0,1). Также будем считать функции полезности активных элементов сепарабельными, т.е. такими, что для каждого активного элемента 1 е I , для любой компоненты его
плана j е J1 и для любых компонент плана х1, х" е R1 и х1_]-, х-;- е RJ1 '{1} таких, что р1 (х'j, х-j) р1 (х, х-j) выполняется р1 (х'j, ~-j) р1 (х, ~-j).
В такой активной системе введем прямой механизм планирования h: RJ ® RJ . По аналогии с индексом состояния АЭ (§ 1 Главы II), определим индекс состояния рj для каждой компоненты плана каждого
активного элемента j е J и каждого вектора точек пика r е RJ следующим образом р j = а если х}- hj (r), р j = m если х}- hj (r) и
рj = c если хj = hj(r). Обозначим через р ер7 вектор состояний всех компонент планов всех активных элементов. Индекс состояния 1 -го активного элемента 1 е I обозначим через р1 = рJ. .
Механизм планирования e : RJi ® RJi, i e I назовем элементарным для i -го АЭ, если для всех компонент плана j e Ji и для всех состояний рj Ф c существуют числа xPj e R{такие, что для любого Г e RJi такого, что Г р j xPj выполняется e}- (r) = xPj и для любого Г e RJi такого, что xc‘ a rj и rj рj xPj . Элементарный
механизм планирования для АЭ с двумерным планом из R2 приведен на рис. 2.3.1, в нем xa = x2a = 0 и x" = x" = 1. Очевидно для любого элементарного механизма выполнено B = Б0.
Ж Г2
(m, m)
(c, m)
'(.
(ac)
d,
(m, a)
(a, a)
Лемма 2.3.1. Пусть функция полезности активного элемента i e I однопиковая и сепарабельная, тогда любой элементарный механизм e : RJi ® RJi неманипулируем. ^
Далее будем считать выполненным следующее условие.
А.2.3.1. Для любого вектора состояний множество Projc(р) Dp является односвязным и существует функция хp :Projc(р) Dp ® RJ такая, что для любого активного элемента i е I величина
J \C (p Jt ) = J \C( p Jt )(rC ( p )\C( p Ji ))- Для любого r е Dp выПолняется
h(r) = хp (rC(p)) и для любого p epJ , Vi е I, VJ е Ji и V~ е Dc(p, J)
найдется r е Dp такой, что xc(p,J)(~C ~ ) = хp (rC(p)) -
Теорема 2.3.1. Пусть функции полезности активных элементов однопиковые и сепарабельные, прямой механизм h: RJ ® RJ ограничен и удовлетворяет условию А.2.3.1, тогда механизм h(r), r е RJ является неманипулируемым. ^
Данная теорема является обобщением результатов работ для механизмов коллективного выбора с векторными альтернативами [7,14,53] и позволяет исследовать неманипулируемость механизмов планирования с векторными планами в терминах множеств диктаторства. В следующем параграфе мы рассмотрим механизм активной экспертизы (МАЭ) и механизм распределения ресурса (МРР), и исследуем их свойства с точки зрения теории реализуемости и множеств диктаторства.
Так же будут рассмотрено соотношение результатов работ [110,111] и результатов § 1 настоящей главы.
§4. Неманипулируемость и реализуемость механизмов активной экспертизы и распределения ресурса
В настоящем параграфе мы рассмотрим МАЭ, МРР а также их обобщения рассматривавшиеся в параграфе 4 главы 1, и установим связь между результатами работ [80,89,111,112] и утверждениями параграфа 2.1. Также приведем результаты работы [113], демонстрирующие возможности применения условий реализуемости (параграф 3 главы 1) в общем виде для исследования реализуемости и неманипулируемости.
Докажем, что прямые механизмы распределения ресурса, определяемые алгоритмом 1.4.1, удовлетворяют условиям А.2.1.1 и
D = D0 . Также проверим выполнение свойств ММ, НСМ, ПО и ОПВ (см. раздел 1.3) для таких механизмов.
Если выполнены условия А.1.4.1-А.1.4.3, то алгоритм, аналогичный алгоритму 1.4.1, примет следующий вид.
На нулевом шаге полагаем s0 = D для всех i = 1, n и получаем распределение ресурса x0 = pi(D, ..., D). Множество Q на нулевом шаге полагаем пустым Q0 = 0 .
На шаге j множество Q1 определяем следующим образом Q1 = {i е I: (x]-1)i rt}.
Для АЭ из множества Q1 по А.1.4.2 определяем s
е W , такие,
QJ
что
Q-
p ,¦ (s ,¦, s1 1) = r
Qjy Qj I\QjJ Q
В конце j - го шага получим
s1 = (s ,, s1 -1.) и x1 = p (s1) .
Q j I \Q j
Если на некотором шаге к окажется, что Qk = Qk-1, то алгоритм останавливается и полагаем s* = sk , x* = хк, Qk = Q .-
| Результаты этого алгоритма обладают следующими свойствами, приводимыми здесь без доказательства (см. [113]). | ||||||||||
|
Лемма 2.3.1. Для механизма распределения ресурса свойство ММ выполнено. ^
Лемма 2.3.2. Для механизма распределения ресурса свойство НСМ выполнено. ^
Лемма 2.3.3. Если d = 0 и ^ D R , то для механизма
ІеІ
распределения ресурса свойство ОПВ не выполнено. В противном случае ОПВ выполнено. ^
Лемма 2.3.4. Для механизма распределения ресурса свойство ПО выполнено. ^
Приведем без доказательств следующие утверждения.
Теорема 2.3.1. Для механизма распределения ресурса,
определяемого алгоритмом 1.4.1, не выполнены условия теорем 1.2.6.1.2.8 и выполнены условия теоремы 1.2.5.
Теорема 2.3.2. Для механизма распределения ресурса,
определяемого алгоритмом 1.4.1, выполнены условия теоремы 1.3.1, и такой механизм распределения ресурса достоверно реализуем.
Теорема 2.3.3. Для механизма распределения ресурса,
определяемого алгоритмом 1.4.1, выполнены предположение А.2.1.1 и условия теоремы 2.1.1, и такой механизм неманипулируем. ^
Следует отметить, что теоремы 2.3.2 и 2.3.3 представляют собой один и тот же результат о неманипулируемости механизма распределения ресурса, определяемого алгоритмом 1.4.1. Так же из теоремы 2.3.1 видно, что хотя необходимое условие реализуемости (теорема 1.2.5) выполнено, достаточные условия реализуемости СГВ, определяемого
рассматриваемым механизмом распределения ресурса, не выполнены.
Для механизмов активной экспертизы, соответствующие прямые механизмы в литературе [111,112] определяются при истинных мнениях экспертов r, упорядоченных по возрастанию, то есть на множествах вида {г е [d, D]n : rx r2 ... rn}. Удобно их описать в терминах перестановок
множества I . Перестановкой множества I называется взаимнооднозначное соответствие t: I ® I.
Пусть задано множество активных элементов I. Рассмотрим перестановки t множества I
1 2 3 ... n \
t1 t2 t3 ... tn 0
которые задают некоторые упорядочения активных элементов. Формально будем писать t: I ® ?, где I - исходное множество активных элементов, ? - упорядоченное множество активных элементов. При этом элементы множества I будем обозначать латинскими буквами, а элементы множества ? будем обозначать греческими буквами. Множество всех перестановок t: I ® ? обозначим через Т . На случай совпадения истинных мнений некоторых экспертов введем разбиения Е множества I на множества Et, l = 1, |e| . Через 3 обозначим множество
всех разбиений E множества I , а через T E множество всех перестановок t е T, переводящих разбиение E множества I в разбиение
X множества ? такое, что для всех l = 1, |e| , Xl = t(El) = {%l,...,%l + \El}, то есть множества Xl представляют из себя последовательное перечисление элементов множества ?. Для каждого разбиения Ег определим последовательность {il }П=1 активных элементов из Ег, такую, что l е{1, ...,|e|}, il = min Г1(а). Определим для каждого разбиения
aeXl
Е е 3 и t е ТЕ следующие множества:
^Е = {r е[d, D]:. l е{1, ..., |Е|} j е Ei, r} = гц и гч гІ2 ... rln}.
Рассмотрим некоторое разбиение Е из 3 и произвольную перестановку t еТЕ . Определим вектор s(a), а е? следующим образом
I s В = d, В = 1, a,
s(a) = | B -
Isb = D, В = (n - a), n, а е?.
Обозначим pt (sj, ..., sn) = p(st(j), ..., st(n)) и для заданных E и t е TE
определим последовательности {Wa }па=1 и {Wa’ E }па=1 следующим образом:
Wa = pt (s(a)) и Wa E = mm WB.
В ех
При заданных разбиении E и перестановке t е ТЕ, для каждого r е ^, соответствующий p (s) прямой механизм h(r) определим следующим образом
h(r) = max min (г , ^, WJe). (2.3.1)
aе? t (a)
Очевидно, что для каждого r е [d, D]n всегда найдутся единственное разбиение E е 3 и единственная, с точностью до перестановок внутри множеств El разбиения E , перестановка t е T E такие, что r effif . Последовательность {W^, Е }па=0 не меняется при перестановках элементов внутри множеств разбиения Е, поэтому механизм h(r) определен для каждого r е [d, D]n однозначно. Нам будет удобно обозначить через W(r) множество элементов из ?, на которых достигается max min (r _j , W^) при данном r е [d, D]n Очевидно, W(r) е x, поэтому обозначим через w(r) такой номер I, что X =W(r).
Свойства введенного механизма описываются следующей леммой.
Лемма 2.3.5. Для любого r е [d, D]n, верны следующие утверждения:
1) если ri h(r), то h(r), h(~, r_t) = h(r) и h(r),
h(~, r_t) h(r);
2) если r h(r), то V~ h(r), h(~, r-i) = h(r) и h(r), h(~, r-i) h(r). ^
Рассмотрим теперь свойства СГВ, определяемой
соответствующим прямым механизмом для механизма активной экспертизы.
Лемма 2.3.6. Для механизма активной экспертизы свойство ММ выполнено. ^
Лемма 2.3.7. Для механизма активной экспертизы свойство НСМ выполнено. ^
Лемма 2.3.8. Для механизма активной экспертизы свойство ОПВ выполнено. ^
Лемма 2.3.9. Для механизма активной экспертизы свойство ПО выполнено. ^
Приведем без доказательств следующие утверждения.
Теорема 2.3.4. Для механизма активной экспертизы,
определяемого (2.3.1), не выполнены условия теорем 1.2.6.-1.2.8 и выполнены условия теоремы 1.2.5.
Теорема 2.3.5. Для механизма активной экспертизы,
определяемого (2.3.1), выполнены условия теоремы 1.3.1, и такой механизм распределения ресурса достоверно реализуем.
Теорема 2.3.6. Для механизма активной экспертизы,
определяемого (2.1.1), выполнены предположение А.2.1.1 и условия теоремы 2.1.1, и такой механизм неманипулируем. ^
| Сводка результатов лемм 2.3.1-2.3.9 приведена в таблице 2.1. Использованы следующие обозначения: символ + означает, что для данного механизма свойство выполнено; символ - означает, что для данного механизма свойство не выполнено. | |||||||||||||||
|
|||||||||||||||
| Таблица 2.1. Свойства соответствующих прямых механизмов распределения ресурса и механизмов активной экспертизы |
Теорема 2.3.7. Пусть прямой механизм H = (ЭТ, h) удовлетворяет
условиям условию А.2.1.1 и для него D = D0, тогда для этого механизма выполнены А.1.2.1, А.1.2.2. ^
Таким образом, условия параграфа 1 главы 2 на структуру множеств диктаторства являются более сильными, чем условия А.1.2.1, А.1.2.2.
Связь между результатами по неманипулируемости механизмов планирования можно отразить следующим образом:
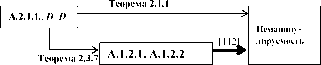
Таким образом, наиболее слабым условием неманипулируемости является НСМ, а наиболее сильным - условия параграфа 1 главы 2. Настоящий параграф устанавливает связь между условиями неманипулируемости механизмов планирования работ [54,89,111,112], обсуждавшихся в § 2-5 главы I, и результатами § 1 главы 2. Кроме этого, показана трудоемкость проверки свойств ММ, НСМ и ОПВ (леммы 2.3.1-2.3.9) для механизмов планирования. При этом оказывается, что только НСМ гарантирует неманипулируемость (Т.2.3.2, Т.2.3.5) рассмотренных механизмов планирования. Условия остальных теорем о реализуемости оказываются невыполенными (Т.2.3.1, Т.2.3.3), что указывает на неэффективность использования аппарата теории реализуемости для исследования механизмов планирования.
Таким образом, в настоящей главе были получены достаточные условия неманипулируемости прямых механизмов планирования а также необходимые и достаточные условия коалиционной неманипулируемости прямых механизмов планирования в терминах множеств диктаторства. Показана эффективность и наглядность применения метода анализа множеств диктаторства для исследования неманипулируемости прямых механизмов.
Глава III. Существование эквивалентных прямых механизмов
При построении механизмов функционирования АС центр может иметь некоторый исходный механизм планирования, в котором сообщение достоверной информации не является равновесием. В таком случае центр может попытаться определить для каждого возможного профиля предпочтений одно из равновесий Нэша и на его основе построить соответствующий исходному прямой механизм.
В настоящей главе приводятся условия, гарантирующие существование эквивалентных прямых механизмов для непрямых механизмов планирования и конструктивно определяется вид эквивалентного прямого механизма.
В § 1 настоящей главы определяется формализм метода множеств диктаторства по отношению к непрямым механизмам. В § 2 приводятся условия существования равновесия Нэша.
В § 3 приводятся общие условия существования эквивалентных прямых механизмов, на основании которых в § 4 строятся конструктивные условия существования эквивалентных прямых механизмов для линейных и дифференцируемых механизмов планирования.
§1. Прямые и непрямые механизмы планирования
Пусть механизм g: S ® Rn не является прямым и для каждого профиля предпочтений j еЭТ с SPn мы знаем одно из положений равновесия s* (j) которое зависит только от положения точек пиков элементов r е Rn. Такие равновесия будем записывать следующим образом: s*(r).
Для непрямого механизма g : S ® Rn построим соответствующий ему прямой механизм. Элементы сообщают информацию ~ е R1, i е I о своих точках пика, центр по ним находит вектор равновесных заявок s* (r) для механизма g : S ® Rn и назначает планы х = g(s* (r)).
Получим новый механизм h(r) = g(s* (r)). Если соответствующий прямой механизм h(r) удовлетворяет условиям теоремы 2.1.1, то он неманипулируем и, следовательно, для непрямого механизма g: S ® Rn существует эквивалентный прямой механизм (см. § 1 главы I)
h(r) = g(s* (r)).
В настоящей главе будем рассматривать непрямые механизмы следующего вида. Пусть планы элементам назначаются по заявкам s) е Sj = [0,1] в соответствии с процедурой планирования
X = g (s'), x е Rn, s = (s1,..., sn) е S = [0,1]n . Будем предполагать, что процедура планирования непрерывна в S и частично монотонна, то есть gj (s) не убывает по st при любых s е S.
В настоящей главе мы получим условия на механизм g: S ® Rn , которые достаточны для того, чтобы соответствующий прямой механизм h(r) удовлетворял теореме 2.1.1, которая гарантирует его неманипулируемость.
Для того, чтобы получить такие условия существования эквивалентного прямого механизма, для каждого возможного профиля предпочтений необходимо найти хотя бы одно равновесное сообщение. Поэтому в следующем параграфе мы докажем теорему о существовании равновесия Нэша для непрямых механизмов планирования.
§2. Существование равновесия Нэша
Рассмотрим непрямой механизм g :[0,1]" ® R". Пусть для
некоторого r е R" существует положение равновесия s* (r). При этом данному r можно сопоставить вектор состояний р такой, что
gc (р )(s* (r)) = rC (р) , gM (р )(s* (r)) rM (р ) , gA( р )(s* (r)) rA( р) . В силу того. что s* (r) - равновесие Нэша, элементы i е M(р) будут сообщать заявки s* е Arg max gi(s',s-), элементы i е A(р), s* е Arg min gi(s',s-) и
s,'e[0,1] s,'e[0,1]
s* е [0,1], i е C(A).
В силу частичной монотонности {s;- = 1}е Arg max gi (s,, s-i) и
s,'е[0,1]
{s;- = 0}е Arg min gi (s',, s-i). Далее будет доказано, что в равновесии
s'i е[0,1]
s* = 1, i е M(A); s* = 0, i е A(A) и s* е [0,1], i е C(A).
Найдем положения равновесия для механизма примера 2.1.1. Пример 3.2.1. Для механизма g1 (s) = s1 + 2 - s2, g2 (s) = s1 + s2,
si е [0, 1], i = 1, 2 , (r1, r2) е R2 найдем одно из возможных равновесий для всех профилей р е SP". Очевидно для всех функций полезности с точкой пика r е D(m, m) вектор сообщений s* = (1, 1) будет равновесием Нэша.
Действительно, пусть r е D(m, m), например r = (4, 3). g(s*) = (3, 2) и, изменяя свое сообщение, первый АЭ не может получить план больший трех, поскольку при g(s1, s2*) 3 для всех si е [0, 1]. Поскольку функция полезности р1 строго возрастает до точки пика r1 = 4 , то р1( g1(s*)) p^g^, s*)). Аналогично s2 е [0, 1],
р2(g2(s*)) p2(g2(s1*, s2)). Тогда s* = (1, 1) является равновесием Нэша для всех профилей предпочтений, задаваемых однопиковыми функциями полезности таких, что их точки пика r1 = 4, r2 = 3 .
Аналогично, для любого профиля предпочтений р е SP", такого, что вектор точек пиков профиля r е D^c m), равновесие Нэша
определяется выражением s* (r) = (r1 - 2, 1). Например, для профиля с точками пиков r1 = 2,5 и r2 = 2. Положение равновесия s* (r) = (0,5; 1).
Действительно, при s* = 0,5, s* = 1, gj(s*) = 2,5, g2(s*) = 1,5. Как видим при таком векторе сообщений первый активный элемент получает максимально возможную полезность и меняя своё сооб^ление ?^і ? [0, 1],
j1(g (s*)) j2(g (s1, s*)). Аналогично невыгодно менять своё сообщение второму элементу, так как s2 е [0, 1) g2(s*) g2(s-*, s2).
Значит s* (r) = (0,5; 1) является равновесием Нэша при r = (2,5; 2).
Приведем выражения для векторов равновесных сообщений, если
r е D(m, m), s* (r) = (1, 1);
r е D(m, c), s* (r) = (1, r2 -1);
r е D(m, a), s* (r) = (1, 0);
r е D(c, a), s*(r) =01 1); r е D(a, a), s* (r) = (0, 0); r е D(a, c) , s* (r) = (0, r2);
r е D(a, m), s* (r) = (0, 1);
r е D(c, m) , s* (r) = (r1 - 2 1) .-
В записи s_j индекс J , где J - подмножество I, обозначает по аналогии с индексом i все компоненты вектора s, которые не принадлежат J .
Для каждого вектора состояний р ер определим вектор spC(р) размерности |і \ С(р)| , с компонентами sP, i е I \ C(р) :
0, i е А(р);
sP = ,
г [1, i е M(р).
Так же, для каждого вектора состояний определим множества
Sр = {s е R : sm(р) sM(р sA(р) sA(р sc(р) е [0, 1]ІС(рр еР.
Для случая двух элементов, разбиение {S р } изображено на рис. 3.1.
Далее нам потребуется некоторые очевидные из геометрических соображений свойства множеств Бр, р ер, доказательства которых приводятся в приложении.