Технология функционирования системы формирования решений
Внутренняя информация касается производства, финансов, основных фондов, оборотных средств, кадров и т.д. Вся перечисленная информация достаточно точна и находится в обязательной бухгалтерской и статистической отчетности.
Внешняя информация отражает состояние дел во внешней сфере и касается рынка, конкурентов, кредитной и таможенной политики государства, мировых тенденций в области финансов и энергоносителей и др. Источником этой информации являются бюллетени, сводки, биржевые отчеты, пресса.
База знаний содержит модели формирования решений, ориентированные на вполне конкретную область. Знания в системе, ориентированной на обратные вычисления, могут быть представлены в следующих формах:
- дерево целей, снабженное формулами расчета;
- дерево вывода;
- дерево вероятностей;
- нечеткие множества.
Модули приобретения знаний и ввода данных содержат в себе систему управления базами знаний (СУБЗ) и систему управления базами данных (СУБД). С помощью СУБЗ создают деревья целей, выводов и вероятностей, корректируют и ликвидируют их.
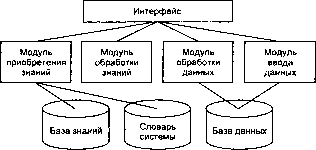
СУБД предназначены для создания баз данных, ввода исходных данных и их корректировки.
Модуль обработки знаний состоит из ряда подмодулей, предназначенных для числовой обработки каждого вида знаний. Работают они автономно.
Модуль обработки данных предназначен для поиска, агрегирования и выполнения предварительных расчетов на основе баз данных.
Пользовательский интерфейс является диалоговой компонентой системы и представляет собой программные и аппаратные средства, которые обеспечивают взаимодействие пользователя с системой. Данный термин охватывает все аспекты взаимодействия пользователя и системы формирования решений.
Он также включает те факторы, которые делают взаимодействие простым, интерактивным и удобным. Недружественность пользовательского интерфейса зачастую является главной причиной того, что менеджеры не используют компьютерную поддержку своей деятельности в полной мере.
Наличие программной оболочки исключает этап программирования, что существенно сокращает трудоемкость и сроки разработки системы. Она позволяет лицу, формирующему решение, оперативно адаптировать систему под новую конъюнктуру рынка, изменения в социальной среде и т.д.
В зависимости от характера принимаемых решений используется та или иная форма базы знаний. Если проблема и цель достаточно определены и могут быть описаны детерминированными зависимостями, то применяется дерево целей. В противном случае, т.е. когда связи между событиями расплывчаты, но могут быть описаны с некоторой долей определенности, применяются деревья вывода и нечеткие множества.
При наличии вероятностной информации можно применять дерево вероятностей.
Перечислим типовые процедуры машинной технологии формирования решения с помощью программных оболочек.
1. Сформулировать проблему, цель или гипотезу, требующие принятия решения, а также критерий оценки альтернатив.
2. Выполнить постановку задачи и выбрать модель базы знаний.
3. Составить словарь системы.
4. Наполнить систему знаниями и данными.
5. Проанализировать полученный вариант (варианты) решения и в случае надобности изменить условия их получения.
Формирование проблемы, цели или гипотезы
Допустим, предприятие характеризуется низкой рентабельностью и высокой себестоимостью продукции, что существенно снижает его конкурентоспособность. Признаками проблемы низкой конкурентоспособности являются сокращение объемов реализованной продукции, снижение уровня заработной платы, а также трудности с получением и возвратом кредитов.
Цель в данном случае состоит в повышении рентабельности до желаемого уровня, определяемого траекторией развития предприятия. В качестве критерия оценки вариантов решений можно выбрать минимум ресурсов, необходимых для достижения цели.
Постановка задачи и выбор модели базы знаний
Согласно сложившейся практике постановка задачи должна содержать описание:
- результирующей информации (что следует получить в результате решения задачи);
- входной информации;
- условно-постоянной информации;
- процедур и алгоритмов преобразования входной информации в результирующую.
В итоге выполнения данной процедуры получают:
- дерево целей с формулами для расчетов, или дерево вывода типа И-ИЛИ с нечеткими множествами;
- ограничения, диктуемые объемами наличных ресурсов;
- перечень первичных документов (бухгалтерских, финансовых, внешних и др.);
- перечень результирующих документов (бумажных, электронных).
Составление словаря системы
Словарь системы - это набор слов, фраз, кодов, наименований, используемых разработчиком для обозначения условий, целей, заключений и гипотез. Словарь - это тот набор слов и обозначений, которым владеет система и благодаря которому пользователь понимает результаты ее работы.
Составление словаря -важная работа, ибо четко сформулированные условия и ответы резко повышают эффективность эксплуатации системы. При составлении словаря и при его вводе в систему следует иметь в виду, что требуется однозначное, без повторений обозначение (или формулирование) только гипотез (главных заключений, находящихся в корне дерева).
Условия и промежуточные выводы могут использоваться в качестве исходных данных для вывода различных гипотез и поэтому их обозначения могут повторяться.
Наполнение системы данными и знаниями
Эта процедура предусматривает отчуждение субъективных знаний у лица, формирующего решение, для настройки системы. Системе следует сообщить:
- приоритеты в достижении цели на различных уровнях дерева, а также шаг и диапазон изменения коэффициентов относительной важности (КОВ);
- ограничения на используемые ресурсы, а также диапазон их изменения;
- критерий, согласно которому следует выбирать вариант решения;
- форму выдаваемой информации (таблица, диаграмма, график и т.д.).
Исходные данные из бухгалтерской, финансовой и другой отчетности, а также информация из внешних источников (ставки рефинансирования, кредитные ставки, таможенные пошлины и т.д.) поступают в базу данных.
Анализ предложенного варианта решения
Система может лишь подготовить вариант (варианты) решения, но не может его принять. Ответственность за принятие решения несет лицо, формирующее решение, поэтому оно должно взвесить все возможные последствия данного шага.
Если возникают какие-либо сомнения либо появились новые соображения, которые можно ввести в систему и получить уточненное решение, то после их ввода система повторно выполняет необходимые расчеты и предоставляет новый вариант решения.
Технология функционирования системы формирования решений
Технологию функционирования системы рассмотрим с помощью интерфейса, указывающего на операции, которые следует выполнить.
Основное меню системы содержит шесть позиций, содержание которых раскрывается с помощью выпадающих подменю. Для разработчика системы предназначены позиции Правила, Ввод, Редактирование, а для пользователя - Ввод, Выполнение, Печать.
В процессе приобретения опыта работы с системой пользователь сам сможет выполнять функции разработчика, так как программирование не требуется.
Позиция Правила позволяет вводить правила при создании новой системы. Чтобы инициировать работу созданного набора правил, предварительно необходимо его загрузить.
Для этого предназначена позиция Загрузитъ, которая после ее выбора предоставляет пользователю возможность указать и загрузить требуемый набор правил.
После ввода нового набора правил возникает необходимость в его сохранении. Сохранить можно под старым именем или новым. Для этого достаточно указать позиции Сохранитъ или Сохранитъ как...
При желании можно отказаться от этих функций нажатием клавиши Esc.
Таблица Ввод знаний предоставляет эксперту возможность ввести следующую информацию:
Гипотезы.
Правила.
Формулы.
База данных.
Терминальные вершины.
Указав первую позицию, пользователь получает на экране макет ввода гипотезы. При этом в случае проверки гипотезы на синонимию он может, нажав клавишу F7, открыть окно словаря использованных гипотез.
После ввода всех требуемых гипотез (ввод их обязателен) эксперт нажатием клавиши Esc может вернуться в главное меню.
Ввод правил с помощью позиции Правила является центральной процедурой системы. Указав данную позицию, пользователь получает меню, в котором следует уточнить тип правила.
Для этого предусмотрена таблица Тип правила.
Выбрав позицию Простое, эксперт получит макет ввода простого правила (рис. 6.4).
Ввод правил, условия в которых связаны логическими операциями ИЛИ/И, выполняется по тому же макету, что и простое правило, однако число выводов не ограничивается.
Некоторые или большинство терминальных вершин могут содержать условия, выполнение которых ведет к изменению содержания самого правила. Если возникла необходимость ввода реляционного выражения, эксперт в окне Тип правила должен указать позицию Реляционное выражение, что обеспечит ему соответствующий макет ввода (рис.
6.5).
В том случае, если реляционное выражение поддерживается формулами, следует указать соответствующую позицию (Формулы). Указав ее, эксперт получает на экране макет ввода формул (рис.
6.6). Просмотр и редактирование уже введенного набора правил осуществляется с помощью специального диалогового окна. Изменение (удаление, редактирование) осуществляется после вызова директории с именами файлов с наборами правил.
Чтобы добавить новое правило, можно воспользоваться таблицей диалога Тип правила, которая, в свою очередь, обеспечит эксперту макет ввода правила.
Ввод реляционного выражения
Тип правила
Коэффициент
определенности
Что выводится из реляционного выражения
Условие
Условие отрицается
да
нет
F7 - Словарь
F2 - Сохранить
Esc - Отказ
Ввод формул
Имя переменной
Выражение, определяющее переменную
F2 - Сохранить
Esc - Отказ
F7 - Словарь
Рис. 6.6
Позиция Выполнение главного меню предназначена для пользователя. Однако, прежде чем запустить систему на выполнение, он должен загрузить тот набор правил, работа с которым планируется.
Загрузка осуществляется в окне Ввод правил. Указав позицию Выполнение, пользователь получает окно с предложением указать, обрабатывать ли все гипотезы данного набора правил или только одну.
Введя в окно свое пожелание, пользователь получает макет ввода значений переменных для использования реляционных выражений и формул. Осуществляется это с помощью таблицы диалога Макет ввода коэффициентов.
Макет ввода представлен на рис.
После окончания ввода всех исходных данных система автоматически производит расчет коэффициента определенности гипотезы. Если в качестве терминальных вершин используются реляционные выражения или формулы, ввод их производится так же, как и простых терминальных вершин.
Результаты расчетов предоставляются в диалоговом окне, форма которого показана на рис. 6.8.
- Результаты расчетов-
Для гипотезы Г_~_
Коэффициент определенности равен [
F1 - ответ на вопрос КАК F1 - ввод иного условия Enter - продолжение
Рис. 6.8
Возникшие сомнения в отношении правильности результатов пользователь может рассеять, нажав клавишу F1. В результате на экране появляется объяснение типа КАК.
Дальнейшее развитие систем, ориентированных на применение обратных вычислений, по всей вероятности, будет направлено на синтез неоднородных баз знаний. Это представляется вполне очевидным, так как человек применяет в своей деятельности множество форм и методов представления и обработки знаний.
Второе направление, которое уже достаточно интенсивно развивается, касается методов, обслуживающих информационные технологии, направленные на обработку информации, поступающей из сети Интернет. Эта информация характеризуется сильной неструктурированностью и разнородностью, однако она необходима для правильного формирования решения. В настоящее время интенсивно развиваются информационные технологии, предназначенные для обработки именно такой информации, названные Интеллектуальный анализ данных (Data Mining).
Ожидается, что эта и другие новейшие достижения в области искусственного интеллекта существенно повлияют на дальнейшее развитие систем формирования решений.
ПРИЛОЖЕНИЯ
| 1. Формулы обратных вычислений для детерминированных зависимостей | ||||||||||||||||||||||||
|
| Целевая установка, пример | Прирост аргументов |
Коэффициенты |
| У = /(*(*), Z( р, р- = Я_(а),ар с-(р) |
П-АП = ~, Ь С-АС = к2 |
и іі ^ д |
| Решение задач на основе единого коэффициента прироста аргументов | ||
| У+ f(x+(,a) z+(P)X Р+ =К+ (а)Ц+ф), а Р. | АК = а?0, AZ| = p^0 |
-(а// + р/С) = d , d±yj(d2 +4офДЯ Кг) 0 2ар |
| у+ = /(*, г~(р)), р+ _ П+{а) с-(р) |
А/7 = а0, АС = Р0 |
ДРС "р(Р + ДР) + а |
| ^+=/(*-(а),г+(Р)), Ф+ =АФ~(а)+ПФ+ф), Р а |
АЛФ = а0, А/7Ф = р0 |
, АФ an ........ 0 р-а |
| у+ = f(x-(а), г-(Р)), р+ _ П~(а) с-(Р) |
АП = а к0, АС = рАг0 |
ь САР 0 Р(Р + Д/)-а |
| у~ = х+(а), г+(р)), П = В-С |
А? = а0, АС = Р*0 |
*.= м р-а |
| У~ f(x~(a), г+(Р)), р- _ П~{а) С+(Р)’ а р |
А/7 = а к0, АС = Р к0 |
7 _П-С(Р-АА) 0 ~ Р(Р-АР) + а |
| У~ = /(*"(а), г"(Р)), Г = К~ (а)-(Г ф) |
АК = ак0, АС = р к0 |
/ф + Са = 7 , d±yjd2 +4арДР ^0 " Л Q 2аР |
| Целевая установка, пример | Прирост аргументов |
Коэффициенты |
| Решение задач без коэффициентов прироста аргументов | ||
| / = /(*+(а),г+(Р)), Я+ = 5+(а)-С+(Р), а р |
АВ = АС, Р АС = ^ "-1 Р |
- |
| у+ = f(x+(a), г'(Р, р+_Я+(а) С(Р) ’ а Р |
ас = (Р + АР)С-П Р+АР+- Р дя = аАС Р |
- |
| У+ = fix'(а), г+(Р)), П+ = П~ (а) + П„ (Р) | аяп=|аяи, АЯИ = Р |
- |
| У+ = /(- *( а), z(P)), /+ _ Б~ (а) (в) |
аа = а+Ы)-б, I + AJ-Р АБ=-АА Р |
- |
| у~ = /(*+(а), г+(Р)), Л' =В+(а)-С+ф), Р а |
А* = ^, Р АС = ^ Р |
- |
| .Г = /(*, г (Р), Я-=Яп+(а) + Яи+(р) | В АЯИ = "-1 Р |
- |
| Целевая установка, пример | Прирост аргументов |
Коэффициенты |
| У~ = /(- *"() г+(Р), П~ = П~ (а) + П* (Р) | АЯП=^, АЯИ=^ "-1 Р |
- |
| У~ = f(x~( а), г~(Р) П~ = Пп(а) + Пн (Р) |
АЯ.-7-, тш~ш і+" Р |
- |
| Решение задач без указания приоритетности целей | ||
| Ь + " 1 ? +* ^ II II + |
В + АВ = кВ, С+АС=кС |
, П + АП к =- Я |
| ¦* ./(-?*,г-) С" |
Л + А/7 = кП С С-АС = к |
|
| y+ = f(x',z+) Л+ =в~-с+ |
В-АВ = ~, к С + АС = кС |
-(А+АА)+(А+АА)2 + U СВ |
| К ' ' 1 2С |
||
| У~ = /(* г) А~ = В~ - С~ |
В-АВ = ~, к г с-дс = - к |
к= А А-АА |
| Целевая установка | Вид задачи |
| P(A + Bf = = P{A{a)f + Р{Вт+ |
Р(А + В) + АР(А + В) = Р(А) + АР(А) + Р(В) + АР(В) АР(А) _ а АР(В)р |
| Р(А + В)+ = | Р(А + В) + АР(Л + Я) = /(Л) + АР(А) + Р(?) - АР(В) і Др( а |
| = Р(Л(а))+ + Р(Д(р)Г | АР(В) Р |
| Р(А + ВУ = = Р(А(а))+ + Р(Вф))~ |
Р(А + В) - АР(А + В) = Р(А) + АР(А) + Р{В) - АР{В) АР(А) а АР(Я) р |
| Р(А + В)+ = = Р(А)+ + Р(В)+ |
Р(А + В) ± АР(А + В) = Р(А)± А Р(А) + Р(Я) ± АР(Я) АР(А) = к Р(А) АР(В) = кР(В) |
| Р(А + В)+ = = Р(А)+ + Р(В)~ |
Р(А + В) + АР(Л + В) = Р(А) + АР(А) + Р(В) - АР(В) АР(А) = к Р(А) АР(В) = кР(В) |
| Р(А + В)+ = = Р(А)+ + Р(В)+ --Р(А)+ - Р(В)+ |
Р(А + В) + АР(А + В) = Р(А) + АР(А) + Р(В) + ДР(В) -¦ -(Р(А) + АР(А))(Р(В)+ДР(В)) АР(А) _ а Д/(Я)"р |
| Р(А + В)+ = = Р(А)~ + Р(В)+--Р(А)~Р(В)+ |
Р(А + В) + АР(А + В) = Р(А) - АР(А) + Р(В) + АР(Я) -- -{Р(Л)-ЬР{А)){Р{В) + Ы{В)) АР(А) _ а Д/(Я) ~ р |
| Целевая установка | Вид задачи |
| Р{А + В)+ = = Р(А)+ + Р(Я)+ - -Р(А)+Р(В)+ |
P{A + B) + AP(A + B) = P(A) + AP(A) + +P(B) + AP(B) - (P(A) - AP(A))(P(B) + AP(B)) ' AP(A) = k-P(A) AP(B) = kP(B) |
| Р(А + В)+ = = Р(А)~ + Р(В)+ --Р(А)-Р{ВГ |
P(A + B) + AP{A + В) = Р(Л) - ДР(Л) + +P(B) + ДЯСЯ) - (Р(Л) - AP(A))(P(B) + AP(B)) ' AP(A) = k P(A) AP(B) = kP(B) |
| P{ABf = = іИ(а))±х хР((В I ЛХр))* |
P(A3)±AP(A-3) = = (P(A)±AP(A))(P(B\A)± . ±A/(?|/Q) АР(Л) a AP(tf) " p |
| P(ABf = = Р(А(а))±х xPUBlAmf |
(Л - 5) ± АР(Л - B) = (/(/*) ± AP(A))(P(B \A)± ±AP(B\A)) AP(A) = k-P(A) AP(B\A) = k-P(B\A) |
| P(ABf = = 7И(а))±х хТЧДф))* |
fР(Л - 5) ± АР(Л - 5) = (Р(Л) ± AP(A))(P(B) ± AP(B)) j AP(A) _ a [др(В)_ p |
| P(ABf = = Р(А)* ¦ Р(В)* |
P(A - B) ± AP(A - 5) = (Р(Л) ± ДР(Л))(Р(Я) ± AP(?)) AP(A) = k-P(A) AP(B) = kP(B) |
| P(Af = P(Hi(a)f х хР(А\Н1) + +Р(Н2(Р)±Р(А\Нг) |
P(A)±AP(A) = (Р(Я,)±ДЯ(Я, ))(Р(Л |Я,) + ¦+(Р(Я2)±ДР(Я2))(Р((|Я2) ЛДЛ) х(Я,) 1 АР(5) " р(Я2) |
| P(Af = PiHrf х xP(A\Hl) + +P(H2)±P(A\H2) |
(Л) ± ДР(А) = (Р(Я,) ± АР(Н\))(Р(А 1 Я,) + +(/(Я2)±Д/(Я2))(/(Л|Я2) ' ДР{Н,) = к Р{Нх) АР(Н2) = к ¦ Р(Н2) |
| Целевая установка | Прирост аргументов (вид задачи) | |
| ct(b)+ = ct+(a) - ct(np) | / \ л / ч ct(b) + Act(b) ct(a) + Act(a)= к к ' ct(np) |
|
| ct(b)~ = ct~ (a) - ct(np) | Ч А „ Ч ct(b)-Act(b) ct{a) Act(a) = ct(np) |
|
| ct(b)+ =ct+mia(a)ct(np) | /л* / ч ct(b) + Act(b) c,min (а)+ Aclmi„ (a) = ct(np) |
|
| ct(b)~ =сГтів(а)сІ(пр) | / ч a / ч ct(b)-Act(b) *min() Дс/тіп(й) = ct(np) |
|
| ct(b)+ =ct*m„(a)ct(np) | / ч a / ч ct(b) + Act(b) е1тЛ") + Ас'™Л")= „ . ct(np) |
|
| ct(b)~ =Ct~aua(p)-Ct(np) | / ч a / ч ct(b)- Act(b) тах() Act^(a) = ct(np) |
|
| ct(k)+ = cf+(a,a)x xct(npl) + ct+ (b, P) x xct(np2) - cf + (a ,a) x xc/(n/il)-c/'(A,P)x xct(npl) |
ct(k) + A ct(k) = (c/(a) + Ac/(a)) - + (c/(Z) + +Act(b)) - ct{npl) - -(ct(a) + Acf(a)) - с/(л/?1) - (cf(?) + Ac/(Z?)) - ct(np2) Act(a) a Acf(fc) P |
|
| ct(k)+ = cf+(a,a)x xcf (/!/ll) + ct~ (b, P) x xct(np2)~ ct+ (a, a) x xcf(/i/jl)cf"(?,P)x xct(np2) |
- | c/() + Act(k) = (cf(a) + Act(a)) - + (ct(b) - -Act(b)) - ct(np2)- -(c/(a) + Act(a)) - c^(/2/?l) - (ct(b) - Act(b)) - ct{np2) A ct(a) a A ct(b) P |
| ct(k)+ = cf"(a,a)x xcf (/i/il) + ct+ (b, P) x xct(np2) - ct~ (a, a) x xct(npl) ct+(b,fl)x xct(np2) |
ct(k) + Act(k) = (c/(a) - Ac/(a)) - c/(h/?1) + (c/(Z?) + +Act(b)) - ct(np2) - -(ct(a) - Act(a)) - ct{np\) - (c^(fc) + Ac/(Z)) - ct(np2) A ct(a) a A ct(b) P |
ЛИТЕРАТУРА
1. Тихонов А.Н. Об устойчивости обратных задач // ДАН СССР. - 1943. - 39(5). - С. 195-198.
2. Пригожий И. Конец определенности. Время, хаос и новые законы природы. - Ижевск: НИЦ Регулярная и хаотическая динамика 2001. - 208 с.
3. Романов А.Н., Одинцов Б.Е. Советующие информационные системы в экономике. - М.: ЮНИТИ, 2000. - 487 с.
4. Марселлу с Д. Программирование экспертных систем на ТУРБО ПРОЛОГЕ. - М.: Финансы и статистика, 1994. - 256 с.
5. Дик В.В. Методология формирования решений в экономических системах и инструментальные среды их поддержки. -М.: Финансы и статистика, 2000. - 300 с.
6. Прикладные нечеткие системы / К. Асаи, Д. Ватада, С. Иван и др.; Под ред. Т. Тэрано, К. Асаи, М. Сугено. - М.: Мир, 1993.-368 с.
7. Саати Т. Принятие решений. Метод иерархий. - М.: Радио и связь, 1993. - 320 с.
8. Турский Е.И. Теория вероятностей с элементами математической статистики. - М.: Высшая школа, 1971. - 328 с.
9. Заде Л. Понятие лингвистической переменой и его применение. - М.: Мир, 1976. - 215 с.
