Решение задач без указания приоритетности целей
Число это следующее: Хх 4; Х2 5.
Так как общее число шаров должно быть равно И, уменьшим число черных на 2. Тогда новое соотношение красных, белых и черных шаров будет следующим: 4, 5, 2.
Проверка. Р(Л + В) + АР(^ + 5) = ~ ~ ~ = 0,8.
На рис. 3.2, б результаты расчетов представлены новым числом шаров: число красных увеличилось до 4, белых - до 5, а черных - сократилось до 2.
2. Целевая установка: Р(А + В)+ = Р(А(а))+ +
Такая целевая установка ориентирует на то, что достичь желаемого результата следует не за счет одновременного увеличения вероятностей наступления событий А и В, а за счет увеличения одной вероятности и уменьшения другой.
Как и ранее, вначале запишем систему уравнений в общем виде, обращая внимание на то, что в соответствии с постановкой задачи прирост вероятности наступления события В имеет отрицательный знак:
'Р(А + В) + АР(А + В) = Р(А) + АР(А) + Р(В) - АР(В),
- АР(А) _ а
ДР(Д)Т
Пр и м е р (рис. 3.3).
Обратимся к предыдущей целевой установке. Пусть, как и ранее, необходимо увеличить вероятность наступления событий А или 5 до 0,8 с коэффициентами приоритетности для события А, равного 0,7, и для события В, равного 0,3.
Однако добиться увеличения общей вероятности необходимо за счет увеличения вероятности наступления события А и уменыне-ния события В. На рис. 3.3, б представлена задача обратных вероятностных вычислений с различной направленностью в изменении аргументов.

Так как старое и новое (желаемое) значения вероятности наступления событий А или В известны, система уравнений приобретает вид:
0,17 = ДР(Л)-ДР(Д)),
- АР(А) 0,7
_др(я)-о,з'
Решив ее, получим:
АР(А) = 0,3;
АР(В) - 0,13.
Новые значения вероятностей наступления событий А или В следующие:
Р(А) + АР(А) = 0,27 + 0,3 = 0,57; Р(В) - ДР(В) = 0,36 - 0,13 = 0,23.
Для того чтобы узнать, какое соотношение шаров может обеспечить такие вероятности, составим уравнения:
Р(Л) + Л/ЧЛ) = ;
П
Р(В)-АР(В) = ^,
П
где, как и ранее, ХуХ2 - новое число красных и белых шаров. Соответственно
Xx6;X23.
В связи с тем что общее число шаров не изменилось, число черных шаров сокращается до двух. Проверка указывает на правильность вычислений:
Р(А + В) + АР(А + В) = + = = 0,8.
11 11 11
На рис. 3.3, б результат вычислений представлен в виде измененного числа шаров красного и белого цветов.
3. Целевая установка: Р(А + В)~ = Р(А(а))+ + Р(5(Р))".
Такая целевая установка ориентирует на определение соотношения шаров, обеспечивающего снижение вероятностей наступления событий А или В, причем вероятность события А должна увеличиться, а вторая, т.е. вероятность наступления события В, должна снизиться. Остальные данные те же, что и в предыдущей задаче.
На рис. 3.4, б представлена графическая интерпретация обратных вероятностных вычислений, предназначенных для уменьшения вероятностей наступления событий А или В.
Запишем нужную систему уравнений, имея в виду задачу уменьшения вероятностей появления событий А или В:
ГР(А + В) - АР(А + В) = Р(А) + АР(А) + Р(В) - АР(В\
АР(А) _ а ЛР(Я)"Р'

Пример. Допустим, новое желаемое значение суммы вероятностей равно 0,5, существующее же равно 0,64; если коэффициенты а и Р равны 0,3 и 0,7 соответственно, то система примет вид:
0,17 = АР(В) - АР(А),
АР(Л) 0,7 АР(В) ~ 0,3
Решив ее, получим:
АР(А) = 0,18;
АР(В) = 0,42.
Новые значения вероятностей наступления событий А или В равны:
Р(Л) +АРМ) = 0,27+ 0,11 = 0,38; Р(В) -АР(В) = 0,36-0,26 = 0,1.
Новые вероятности обеспечиваются следующим соотношением шаров:
р(Л)+др(Л) =;
П
Р(В)-АР(В) = ^,
П
где, как и ранее, Х{, Х2 - новое число красных и белых шаров соответственно.
Число красных шаров должно быть равно Хх 4, а белых -Х2 1 (рис. 3.4, б).
Так как общее число шаров равно 11, черных шаров будет 6.
Проверка. /(Л + Д)-ДР(Л + Д) = д + д = ^ = 0,45, что на 0,05
меньше желаемого значения. Такая погрешность вполне приемлема.
Здесь следует отметить, что на исходные данные существуют ограничения. В данной задаче для того, чтобы не получить отрицательные вероятности, накладывается ограничение вида а р. Кроме того, желаемый прирост для АР(В) должен быть таким, чтобы разность Р(В) - АР(В) не получилась отрицательной.
Решение задач без указания приоритетности целей
В данном разделе используются сведения из разд. 2.4.
4. Целевая установка: Р(А + В)+ = Р(А)+ + Р(В)+.
Задача обратных вероятностных вычислений принимает следующий вид:
7\А + В) ± АР(А + В) = Р(А) ± АР (А) + Р(В) ± АР(В\
АР(А) = к Р(А),
АР(В) = кР(В),
где к - коэффициент, позволяющий определить искомые приросты вероятностей.
Остальные обозначения прежние.
Пример. Воспользуемся целевой установкой 1. Отличие состоит в том, что информация о приоритетах направлений достижения цели отсутствует.
Это значит, что коэффициенты а и Р либо неизвестны, либо несущественны.
Допустим, у лица, формирующего решение, в качестве цели фигурирует стремление к увеличению вероятности наступления события А или В до 0,8. Графическая интерпретация задачи та же, что и на рис.
3.2, за исключением того, что коэффициенты а и Р отсутствуют.
Так как желаемое значение Р(А + В) + АР(А + В) известно и равно 0,8 и известны также значения: Р(А) + Р(В) = 0,63; Р(А) = = 0,27 и Р(В) = 0,36, система приобретает следующий вид:
0,17 = АР(Л) + АР(В),
АР(А) = к-0,27,
АР(В) = к 0,36.
Решив ее относительно получим к = 0,27.
Новые значения вероятностей событий А и В равны:
Р(А) + АР(А) = 0,27 + 0,27 - 0,27 = 0,34;
Р(В) + АР(В) = 0,36 + 0,27 - 0,36 = 0,46;
Новое соотношение шаров следующее:
Р(А)+АР(А) = ^-,
Р(В) + АР(В) = Ь-,
Хх 4; Х2 5.
Таким образом, мы получили тот же ответ, что и в целевой установке 1. Произошло это из-за довольно сильного огрубления результатов расчета, так как число шаров должно быть целым. При других постановках результаты, как правило, отличаются.
5. Целевая установка: Р(А + В)+ =Р(А)+ +Р(В)~.
При такой целевой установке обратная задача обратных вычислений запишется следующим образом:
Р(А + В) + АР( А + В) = Р(А)+АР(А) + Р(В) - АР(В), АР(А) = к-Р(А),
АР(В) = кР(В).
П р и м е р. Теперь рассмотрим, каковы будут результаты, если одна из вероятностей, например наступления события А, должна увеличиться, а другая - уменьшиться. При этом сумма этих вероятностей, т.е. вероятность наступления события А или В, должна увеличиться и достичь величины 0,7.
Вероятность наступления события А равна 0,36, а события В - 0,27.
Подставив эти данные в систему уравнений, получим:
0,07=ЛР(А) - АР(В),
ЛР(Л) = А 0,36,
АР(В) = к 0,27.
Решив систему относительно к, получим к = 0,78. Приросты равны:
/*(,4)+ДР(Л)=0,36+0,36 0,78 = 0,64,
Р(В) - АР(В)=0,27 - 0,27 - 0,78 = 0,06.
Теперь определим новое соотношение шаров:
Р(А)+АР(А)=^-,
Р(В)-АР(В) = ^,
Хх*1\Х2*\.
Таким образом, красных шаров 7, белых - 1, а черных - 3 (разность 11-8).
Проверка. Р(А + В)+АР(А+В) = 1+1=А=0,7.
Здесь, как и ранее, необходим предварительный анализ исходных данных, так как существует возможность получения бессмысленных результатов. Прежде всего это касается вероятности наступления события А, которая должна быть больше вероятности наступления события В. Это требование вытекает из определения вероятности, которая не может быть меньше нуля.
Кроме того, желаемое значение АР(А) не может превышать определенного уровня, что также может привести к отрицательным значениям вероятностей.
Поиск безусловной вероятности наступления одного из совместных событий
3.3.1.Решение задачи без коэффициентов прироста
Известно, что вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей событий без вероятности их совместного появления, т.е.
Р(А + В) = Р(А)+Р(В) - Р(А) - Р(В).
С практической точки зрения приведенная формула для вычисления безусловной вероятности наступления совместных событий для событий, число которых больше двух, неудобна. Поэтому можно воспользоваться иной формулой:
р(а+в)=\-р(а)р(в\
где А, В - события, противоположные событиям А и В.
Тогда формула для обратных вычислений примет вид:
Р{А + В)± АР(А + В) = 1-(Р(А)± АР(А))(Р(В) ± А Р(Ё).
Здесь следует обратить внимание на то, что приросты вероятностей противоположных событий поменяли знаки:
+АР(Л),+АР(Д).
Пр и м е р . Прямые расчеты приведем из [8], а затем выполним обратные вычисления: производится два выстрела по одной и той же мишени. Вероятность попадания для первого выстрела равна 0,6, для второго - 0,7.
Найти вероятность того, что в мишени будет хотя бы одна пробоина.
Пусть А - событие, при котором будет попадание при первом выстреле, В - попадание при втором, т.е. Р(А) = 0,6; Р(В) = 0,7.
События А и В независимые, но совместные. Тогда вероятность попадания при первом или втором выстреле равна:
Р(А + В) = Р(А) + Р(В) - Р(А)Р(В) = 0,6+0,7 - 0,6 - 0,7 = 0,88, или
Р(+В) = 1 - Р(А)Р(В) = 1 - 0,4 - 0,3 = 0,88.
В общем виде задача поиска безусловной вероятности наступления одного из совместных событий записывается в виде:
Р(А + В)±АР(А + В) =
= Р(А)±АР(А) + Р(В)±
±АР(В)-(Р(А)±АР(А))(Р(В)±Р(В)\
АР(А) _ а АР(В)~р'
6. Целевая установка:
Р(А + В)+ = Р(А(а)Т + Р( В(Р))+ - Р(А(а))+ Р(В(/1))+.
Такая целевая установка в виде задачи обратных вычислений отразится следующей системой уравнений:
Р(А + В) + АР(А + В) =
= Р(Л) + ДР(Л) + Р(Д) +
+Р(В)-(Р(А) + АР(А))(Р(В) + АР(В)),
АР(А) _ а ДР(Д)~р‘
Обозначения прежние.
Пример (рис. 3.5). Продолжим рассмотрение предыдущего примера, но уже будем решать противоположную задачу.
Допустим, что требуется узнать, какие должны быть вероятности Р(А) и Р(В), позволяющие увеличить вероятность Р(А + В) с 0,88 до 0,92. При этом часть прироста вероятности Р(А + В) должна происходить за счет увеличения вероятности Р(А) пропорционально коэффициенту а = 0,7, а увеличения вероятности Р(В) - пропорционально коэффициенту Р = 0,3.
Графическая интерпретация решения задачи поиска безусловной вероятности наступления совместных, но независимых событий представлена на рис. 3.5,6.

Подставив исходные данные в систему уравнений общего вида, получим:
0,04 = 0, ЪАР(А) - 0,4АР(В) - АР(А)АР(В),
АР(А) а ДР(Я)~р'
Решив его относительно АР(А) и АР (В), получим:
0,4р+0,За-?(0,4р+0,За)2-4ар0,04
2а
АР{А) = ±АР(В\
АР( Л) = 0,1; АР(В) = 0,043.
Проверка. АР(А) = 0,1; АР(В) = 0,043; Р(Л) + АР(А) = 0,7; Р(В) + + АР(В) = 0,743; Р(А + В) + АР(А + В) = 0,7 + 0,743 - 0,7 - 0,743 = = 0,924 0,92.
Пример. Вначале рассмотрим прямую задачу.
Токарь обслуживает два станка, работающих независимо один от другого. Вероятность того, что первый станок в течение часа не потребует внимания токаря, равна 0,6, а второго станка - 0,5.
Какова вероятность того, что в течение часа хотя бы один станок не потребует внимания токаря?
Обозначим через А событие, выражающее искомую вероятность, а через Ах и А2 события, заключающиеся в том, что оба станка в течение часа не потребуют внимания токаря. Все события независимы, но совместны.
Их вероятности равны Р(А) = 0,6 и Р(В) = 0,5. С учетом принятых обозначений имеем:
А = + А2,
Р(А) = Р(А1+А2).
Для прямых вычислений воспользуемся противоположными событиями, которые формулируются следующим образом: ни одни станок не проработает без вмешательства токаря. Тогда
а = ага2,
Р(АХ) = 1 - Р(А{) = 1 - 0,6 = 0,4,
Р(А2) = 1 - Р(А2) = 1 - 0,5 = 0,5.
Из независимости событий АхиА2 следует независимость противоположных им событий Д и Д,. Согласно правилу умножения вероятностей независимых событий имеем:
Р(А) = Р(АХ Л2) = 0,40,5 = 0,2.
Отсюда вероятность того, что в течение часа хотя бы один станок не потребует внимания токаря, равна:
Р(Л) = 1-Р(І) = 1-0,2 = 0,8.
Теперь рассмотрим противоположную задачу. Допустим, необходимо узнать условия, при которых вероятность того, что хотя бы один станок не потребует внимания токаря, повысится до 0,92.
При этом приоритетность наступления событий остается прежней: для А она равна 0,7, а для В - 0,3. Согласно рассматриваемой целевой установке запишем систему уравнений, предварительно подставив и преобразовав исходные данные:
0,12 = 0,5 АР(А) + 0,4 АР(В) - АР(А)- АР(В),
АР(А) __ 0,7 АР(В) 0,3
Отсюда искомые приросты: АР(В) = 0,088; АР(А) = 0,21; Р(В) + + АР(В) = 0,588; Р(А) + АР(А) = 0,8; Р(А + В) + АР(А + В) = 0,588 + + 0,8 - 0,588 - 0,8 = 0,918 ~ 0,92.
В результате получен следующий ответ: для того чтобы вероятность того, что хотя бы один станок не потребует внимания токаря, повысилась до 0,92, необходимо повысить вероятность Р(А) до 0,81, а Р(В) - до 0,588.
Здесь, в отличие от предыдущих примеров, в условии задачи не указаны мероприятия или характеристики объектов, от которых зависят исходные вероятности. Поэтому обратные вычисления на этом заканчиваются, и перечень необходимых мероприятий, позволяющих повысить исходные вероятности, не приводится.
Решение задач без указания приоритетности целей
Напомним, что задача обратных вычислений, решаемая для поиска безусловной вероятности наступления одного из двух совместных событий, в общем виде записывается следующим образом:
Р(А + В)± АР(А + В) = Р(А) ± АР(А) + Р(В) ±
± АР{В) - (Р(А) ± АР(А))(Р(В) ± АР{В)\
* АР(А) = к-Р(А\
АР(В) = кР(В).
Обозначения прежние.
7. Целевая установка:
Р(А + В)+ = Р(А)+ + Р(В)+ - Р(А)+ Р(В)+.
Будем считать, что повышение вероятности попаданий должно достигаться за счет снижения вероятности первого попадания, но повышения второго. Тогда система неравенств запишется следующим образом:
Р(А + В) + АР(Л + В) = Р(А) + АР(А) + Р(В) +
+АР(В) - (Р(А) - АР(А))(Р(В) + АР(В)1 4 АР(А) = к Р(А),
АР(В) = кР(В).
Пр и м е р . Воспользуемся исходными данными из предыдущего примера. Подставив их, получим следующее уравнение:
0,ЗА2-0,5А + 0,12 = 0,
откуда к = 0,29; АР{А) = 0,29 - 0,6 = 0,174; ДР(В) = 0,29 - 0,5 = = 0,145; Р(А) + ДР(А) = 0,774; Р(В) + ДР(В) = 0,645.
Проверка. Р(А + В) + ДР(А + В) = 0,92.
8. Целевая установка:
Р(А + В)+ = Р(А)~ + Р{В)+ - Р(А)~ Р{ВУ.
Система уравнений для решения обратной задачи примет вид:
Р{А + В) + ДР{А + В) = Р(А)~ ЛР(А)+Р{В) + +ДР(5)-(Р(^)-ДР(^))(Р(5) + ДР(5)),
' АР(А) = к-Р(А),
ДР(В) = кР(В).
Пример. Воспользуемся исходными данными предыдущего примера, однако будем считать, что повышение вероятности попаданий должно достигаться за счет снижения вероятности первого попадания и повышения второго. Подставив известные величины в систему уравнений, получим:
0,12 = -0,5 ДР(А) + 0,4 ДР(5) + ДР(А)- АР(В),
АР(А) = к О,6,
АР(В) = кО,5.
Решив квадратное уравнение
0,ЗА2-0,1A-0,12 = 0,
получим к = 0,82; ДР(А) = 0,6 - 0,82 = 0,49; ДР(В) = 0,5 - 0,82 = = 0,41; Р(А) - ДР(А) = 0,6 - 0,49 = 0,11; Р(В) + АР(В) = 0,5 + 0,41 = = 0,91.
Проверка. Р(А + В) + АР(А + В) = 0,11 + 0,91 - 0,11 - 0,91 = 0,92.
Поиск условной вероятности совместного наступления событий
Известно, что вероятность совместного наступления двух событий А и В равна вероятности наступления события А, умноженной на условную вероятность события В, вычисленную в предположении, что событие А уже произошло, т.е.
Р(А-В) = Р(А)-Р(В\А),
где Р(А) - вероятность наступления события А;
Р{В\А) - условная вероятность наступления события В, вычисленная в предположении, что событие А уже произошло.
Решение задачи без коэффициентов прироста
9. Целевая установка:
Р(А ¦ Bf = P(A)(a)f ¦ Р((В | ЛХр))*.
На основании формулы совместного наступления двух событий запишем задачу обратных вычислений следующим образом:
Р(А - В) ± АР(А - В) = (Р(А) ± АР(А))(Р(В | А) ± АР(В \ А)),
АР(А) _ а АР(Д)-р’
где Р(А - В) РІА), Р(В) А Р(А - В)
АР(В\А)
АР(А), АР(В)
а, Р
вероятность совместного наступления событий А и В; вероятности наступления независимых событий А и В; желаемый прирост (положительный или отрицательный) вероятности совместного наступления событий А и В;
прирост вероятности свершения события В при условии, что событие А свершилось;
приросты вероятностей наступления независимых событий А и В соответственно;
коэффициенты приоритетности в наступлении событий А к В соответственно.
Пр и м е р . Для иллюстрации процесса решения обратной задачи рассмотрим вначале следующую прямую задачу. В урне 12 шаров, из них 4 белых и 8 красных.
Два белых шара и четыре красных помечены голубой полоской. Какова вероятность извлечения красного шара с полоской.
Обозначив буквой А событие извлечения красного шара, а буквой В - то, что красный шар имеет голубую полоску, можно найти искомую вероятность
Р(А - В) = Р(А) ¦ Р(В\А) = ~ I = і = 0,33.
Допустим, необходимо увеличить вероятность извлечения красного шара с полоской до 0,5. Причем большей частью - за счет повышения вероятности извлечения красного шара (а = 0,6) и меньшей частью - за счет того, что этот шар будет с голубой полоской (Р = 0,4). Обе вероятности должны увеличиваться. Графическая интерпретация противоположной задачи обратных вычислений условной вероятности представлена на рис.
3.6.
Сплошная дуга, связывающая линии графа, указывает на то, что речь идет о появлении обоих событий (А и В).
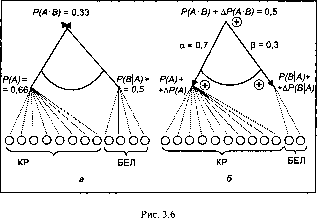
Для решения задачи обратных вычислений вначале запишем систему уравнений в общем виде:
Р(А ¦ В)+ АР(А ¦ В) = (Р(А) + АР{А)){Р{В \А) + АР(В | А)),
¦ АР (А) _ а АР(В)~р'
Подставив известные величины, получим:
0,5 = (0,66+АР(А)Х0,5 + АР(В I А)),
- АР(А) 0,6
АР(2?|Л)_ 0,4
Решив данную систему получим:
АР(А) = 0,16; АР(В \А) = 0,12,
Р(А) + АР(А) = 0,66 + 0,16 = 0,82,
Р(В\А) + АР(В\А) = 0,5 + 0,12 = 0,62.
Проверка. Р(А ¦ В) + АР(А ¦ В) = 0,82 - 0,62 = 0,51 0,5.
Теперь найдем соотношение шаров, которое должно обеспечить желаемый прирост вероятности:
красных: Р(А)+АР(А) = ^ 10; красных с полоской: Р{В\А)+АР(В\А) =
На рис. 3.6, б показано новое соотношение шаров после выполнения обратных вычислений.
Число белых шаров сократилось до 2, для того чтобы общее количество шаров было неизменным, а именно 12.
Решение задач без указания приоритетности целей
10. Целевая установка:
Р(А ¦ В)* = P{Af ¦ Р(В I Af.
Как и прежде, составим систему уравнений вида:
Р(А ¦ В) ± АР(А ¦ В) = (Р(Л) ± АР(А))(Р(В \ А)± АР(В \А)),
АР(А) = к Р(А),
АР(В\А) = к-Р(В\А).
Решая эту систему, необходимо вначале выяснить, имеет ли она решение, так как зависимые события более чувствительны к исходным данным по сравнению с независимыми.
Поиск условной вероятности совместного наступления независимых событий
Известно, что вероятность совместного появления независимых, но совместных событий равна произведению вероятностей этих событий:
Р(АВС-...) = Р(А)Р(В)Р(С)-....
3.5.1.
Решение задач без коэффициентов прироста
11. Целевая установка:
Р(АВ)± = Р(А(а))±Р(Вт±-
На основании формулы появления двух независимых, но совместных событий задачу сформулируем следующим образом:
'Р(Л - В) ± АР(А - В) = (Р(Л) ± АР(А)){Р(В) ± АР{В)\
АР(А) _ а АР(Я)р’
Обозначения прежние.
Решение задач без указания приоритетов целей
12. Целевая установка: Р^АВ)* = /(/1)± - /(fi)±.
Задача, в которой приросты будут определяться с помощью единого коэффициента, принимает вид:
' Р(А ¦ В) ± АР(А ¦ В) = (Р( А) ± АР(А))(Р(В) ± АР(В)),
¦ АР(А) = кР(А),
АР(В) = кР(В).
Обозначения прежние.
Поиск вероятности наступления события совместно с одним из ряда несовместных событий (полная вероятность)
Обратные вычисления оказываются чрезвычайно полезными при принятии решений, касающихся наступления некоторого события совместно с другими событиями, обычно называемыми гипотезами. Речь идет о формуле полной вероятности
P(A)=fjP(Hi)P(A\Hi),
І=1
где Р(Л) - вероятность наступления события А;
Р(Н) - вероятность осуществления гипотезы
Р(А I Нх) - условная вероятность наступления события А при осуществлении гипотезы
3.6.1.
Решение задач без коэффициентов прироста
13. Целевая установка:
P(Af = Р(Я, (о))1 - Р(А I Н1)+Р(Н2 (Р))1 - Р(А IН2).
При наличии двух гипотез задача обратных вычислений может быть сформулирована в следующем виде:
Р{А) ± АР(А) = (Р(НХ) ± АР(Н,) ± АД Я, ))ДЛ|Я,) + (Р( Я2 ± А Р(Н2 ))Р(А | Я2), - АР{НХ) а{Нх)
ар(я2) р(Н2У
где а(Я{), Р(Я2) - коэффициенты приоритетов осуществления гипотез Я{ и Я2 (сумма их равняется единице).
Вполне реальны задачи управления не только безусловными, но и условными вероятностями; для решения таких задач необходима информация о приоритете наступления события при осуществлении той или иной гипотезы. Тогда в систему уравнений необходимо добавить информацию о пропорциях в изменении приростов условных вероятностей. Такая задача примет вид:
'Р(А) ± АР{А) = (Р(Н,) ± АР(Н, ))(Р(А I Я,) ±
±АР{А\ Я, )){Р{Н 2)) ± А Р(Н2 ))(Р(А \Н2)±АР(А\Н2)\ АР{НХ) _а{Н,)
А Р{Н2) р {Н2У АР(А 1Я1) у (Я,)
АР{А\Н2)) 5 (Я2)’
где АР(Д I Я|), АР(Д | Я2) - приросты условных вероятностей наступления
события А при осуществлении гипотез Я1 и Я2 соответственно;
у(Я|), 8(Я2) - коэффициенты приоритетности наступления
события А при осуществлении гипотез Я] и Я2 соответственно.
Остальные обозначения прежние.
В общем случае в рассматриваемой задаче может фигурировать не две гипотезы, а больше. Тогда задача должна быть записана с учетом нормирования коэффициентов приоритетности, что является условием применения процедуры свертки/развертки.
Пример (рис. 3.7).
В начале рассмотрим прямую задачу.

В цехе два типа станков производят одни и те же детали. Производительность станков одинакова, но качество выпускаемой продукции различное: первый тип станков дает 0,90, а второй -0,75 продукции отличного качества. Вся продукция содержится на складе.
Число станков первого типа 7 шт., а второго - 3 шт. Определить вероятность того, что взятая наугад продукция окажется отличного качества.
Пусть А - событие, состоящее в том, что взятая наугад продукция отличного качества. Имеются также две гипотезы:
Н{ - взятая продукция произведена станками первого типа;
Н2 - то же станками второго типа.
Тогда
Р(Н,)=;Р(Я,)=. 1 10 2 10
Условные вероятности события А при этих гипотезах следующие:
Р(Л|#,) = 0,90; Р(Л|#2) = 0,75.
Тогда по формуле полной вероятности
Р(А) = 0,7-0,9 + 0,3-0,75 = 0,825.
Теперь допустим, что существует необходимость повышения Р(А) до 0,91. Каковы при этом должны быть соотношения станков, если приоритетность в изменении станков следующая: число станков первого типа должно увеличиваться пропорционально коэффициенту а = 0,6, а второго - уменьшаться пропорционально коэффициенту (3 = 0,4.
Графическая интерпретация обратных вычислений в случае применения формулы полной вероятности представлена на рис. 3.7, б.
Для решения задачи составим систему уравнений:
'Р(А) + АР(А) = (Я(Я,) + ДР(Я, ))Р(А | Я,) + (Р(Я2) - АР{Н2 )Р(А \ Я2)),
- АР(Я,) _ а(Я,)
АР(Н2) Р(Я2)'
Решая эту систему, следует тщательно проанализировать область значений исходных данных, при которых задача имеет смысл.
3.6.2.
Решение задач без коэффициентов прироста
14. Целевая установка:
P{Af = Р{НХ f ¦ Р{АIHt)+P(H2 f Р(АIН2).
В соответствии с общей постановкой задач данного класса запишем следующую систему уравнений:
Р(А) ± АР(А) = (Р(Я,) ± ДР(Я, ))Р(А I Я, )(Р(Я2) ± АР(Н2 )Р(А \ Н2)),
- Ы{Н,) = к Р{Н,\
АР(Н2) = кР(Н2).
Обозначения прежние.
Поиск вероятности, характеризуемой функцией или плотностью распределения
До сих пор изучались случайные события, качественно характеризующие результаты опыта. Теперь можно рассмотреть результат опыта, характеризуемый количественно.
Как известно, случайную величину можно представить с помощью функции распределения. Если известна функция распределения, то задача обратных вычислений может быть решена с помощью следующей системы уравнений:
((*, ± Ах,) X {хг ± Лх2)) = F(x2 ± Ах2 ) - F(xx ± Ах,), Ахх _ а
где F - функция распределения случайной величины х;
