Решение задач без процедуры свертки/развертки
у = у + Х; Е+=Т+(у)Ф+(Х).
Приросты для аргументов П и D равны:
П + АП = к,П; D + AD = k7D;
к2Р
-Р(аП - оР) + уІ(-Р(сП - оР))2 + 4а сРПР(Р + АР)
1 2 oDP ‘
С целью определения приростов для С и Е предварительно выполним для них нормализацию весов:
Р+? Р+?
Тогда приросты:
D + AD k4D ’
С + ДС = ?,С; Е + АЕ = клЕ\ к,=
кА =
-?(?|і’С - р '?) + 7(0(\|'С - Р'?))2 + 4р'? - С - Е(Р + АР)
Приросты соответственно будут:
Т + АТ = к5Т; Ф + АФ = к6Ф; *6=?±М,
А:5?
_ - у'Ф) + yj(E(k'T - у'Ф))2 + 4у'Х'ЕТФ(Е + АЕ)
5 21'ФЕ
Пример (рис. 2.26). Норматив Р на незавершенное производство рассчитывается по формуле
Р = ПСТ,
где П - однодневный расход материалов;
С - длительность производственного цикла (дни);
Т - коэффициент нарастания затрат в незавершенном производстве.
Допустим, необходимо увеличить норматив за счет повышения всех составляющих формулы расчета. Это отразится следующим образом:
Р+=77+(а)С+(Р).Г(у).
Свернуть эту формулу можно следующим образом:
Р+ = /7+(а)Р+(о),о = р + у, D+ = С+ф) + Г+(у). Приросты для Пи D равны:
р + др
/7 +Д/7 = кхП\ D + AD = кгО\ кх =-,
к2 =
-Р(аП-aD) + у](-Р(аП - aD))2 + 4ааРПО(Р + АР) __
Для определения приростов С и Г предварительно следует нормировать веса аргументов:
P + Y P+Y
Отсюда приросты равны:
С + АС = к,С; T+AT=kJ; к, =
Р' = -?-; Y' = - У
D + AD k4D ’
к4 =
-D(y'C - Р 'Е) + 7(-?(y'C - Р'Г))2 + 4Р'у 'TDC(D + AD) 2Р 'TD '
Проверка. Р = 400; АР = 50; П = 20; С = 4; Т=5;а = 0,6; Р = 0,3; Y = 0,1; D = 20; р' = 0,75; І = 0,25; а = 0,4; = 1,072; к2 = 1,049;
П + АП = 21,44; Z) + ДП = 20,98; А:3 = 1,045; кА = 1,0038; С + ДС = = 4,18; Т+ АТ= 5,019; Р + АР = 21,44 - 4,18 - 5,019 = 449,798 450.
Кратные функции
29. Целевая установка: Р+ = а р+у; у р.
В (Р)
С~( у)
Вначале свернем эту функцию следующим образом:
+ А+( а) В+ф)
" ~ где ~ г-1 \ ' 0_Р + 7-
D~(a) С (у)
Приросты для А и D равны:
A + AA = ktA; D-AD = , ? к,=а + Р
аР + -
к_ 2 кхР 1 „ аР
Р + АР
Для того чтобы определить приросты В и С, необходимо нормализовать их веса:
Р
P+y’
Р' =
y' =
В связи с тем что приросты аргументов В и С определяются умножением, задача решается на основе функции:
D-AD = B+®')C~{y').
С
Тогда приросты В + АВ = къВ, С - АС = можно найти за счет:
кА(Р- АР)
3 D ’
*4 =
CP' + By' + у](СР' + By’)2 - Ay®'(D - AD) 2у'р '(D-AD)
Пример (рис. 2.27). Р = 5; АР = 3; А = 100; В = 5; С = 4; ? = 20; а = 0,6; р = 0,3; у = 0,1; р' = 0,75; Y = 0,25; к= 1,095; к2 = 1,46; А + АА = 109,5; D - AD = 13,7; *3 = 1,3289; кл = 1,94;
5 + ДЯ = 1,3289 - 5 = 6,6445; С-ДС = -^- = 2,06; Р+АР = 109,5 :
1,94
: 6,6445: 2,06 = 7,999 * 8.
Смешанные функции
30. Целевая установка: Р+ = Я+(а)+Л+(Р)-С+(у).
Здесь одновременно имеем дело с аддитивной и мультипликативной функциями. Свернем смешанную функцию:
Р+ = П+ (а) + D+ (о), где о = Р + у, D+ = А+ (Р) - С+ (у).
Приросты для аргументов П и D равны:
П + АП = кхП\ D + AD = k2D;
К _(Р.:+АР)-к{П , а(Р + АР) + аП-аО
/С. .
2 D П
Приросты для А и С определяются так:
А + АА = къП\ С+АС=к4С; к4=^~’
Р(у'А-рС) + уІ(Р(у'А-рС))2 +4$'у'РАС(Р + AD)
3~ 2y'DIT ‘
П p и m e p. P - 44; AP = 10; П = 20; Л = 6; C = 4; D = 24; a = 0,4; P = 0,2; у = 0,4; P' = 0,33; Y = 0,66; = 1,2; k2 = 1,25; П + АП =
= 1,2 - 20 = 24; Z + AZ) = 1,25 - 24 = 30; къ = 1,059; к = 1,179; A + AA = = 1,059 - 6 = 6,3588; C + AC = 1,179 - 4 = 4,716; P + AP = 24 + + 6,3588 - 4,716 = 53,988 = 54.
Решение задач без процедуры свертки/развертки
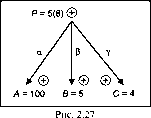
Этот метод предполагает решение системы уравнений, число которых равно числу аргументов функции. Рассмотрим функцию с тремя аргументами.
31. Целевая установка: у+ = /(*+(а), г+(Р), /Г (у)).
Если для расчета приростов аргументов воспользоваться индивидуальными коэффициентами, то получим:
х+Ах = кхх, z + Az = Jc2z,
рлАр = ~. къ
Задача обратных вычислений запишется в виде:
У + Ау = Дкхх,к2г,^-),
h
а
рТ?
к^х-х
к2г-гл р-
к2г г кхх-хл р-
Р
Р_ а+у к3
Ограничения на значения исходных данных устанавливаются из семантики индивидуальных коэффициентов:
*,1, к2 1, к3 1.
Пример. Вложения во внеоборотные активы П, как правило, состоят из приобретения объектов основных средств Р, приобретения нематериальных активов О и приобретения земельных участков В. Формула расчета следующая:
я = р+о+р.
Допустим, целевая установка следующая: необходимо повысить общие вложения во внеоборотные активы за счет увеличения объектов основных средств, наращивания нематериальных активов и сокращения стоимости земельных участков. Все это отражается на формуле следующим образом:
П+ = Р+(а) + 0+(Р) + Р~(у),
где а, (3, у - коэффициенты относительной важности целей, отражаемых аргументами Р, О и В. Соответственно задачу будем решать с помощью индивидуальных коэффициентов:
Р + АР = кхР,
0 + Ш = к209
В-АВ = .
h
Запишем задачу обратных вычислений:
П+АП = к,Р+kjO н,
2
к{Р-Р _ а
ЬО-О+В- P+Y
к20-0
к^-Р+В-
Решив данную систему относительно к? к2 и ку можно получить приросты для аргументов Р, О и В.
2.7.
Комплексный пример применения обратных вычислений в экономике
В качестве примера выберем предприятие, руководство которого озабочено низким уровнем рентабельности. При этом оно осознает пути повышения рентабельности и способно указать приоритеты в выборе этих путей.
Дерево целей (см. рис. 1.2), формулы для прямых расчетов и числовые значения исходных показателей рассматривались в разд. 1.1. На рис.
1.3 с помощью знаков плюс и минус показаны направления изменения аргументов. Приоритетность целей представлена в табл. 2.1.
Для того чтобы расчетные формулы к рис. 1.3 можно было использовать для обратных вычислений, их необходимо снабдить целевыми установками.
Приведем их.
* ’ Ф+(Р) + Г(у)'
Для расчета Р выполним свертку: Д~(Р + у) = Ф+(Р) + 9(у) и введем индивидуальные коэффициенты:
Я + Л/7 = Я,
Д-АД = ^-, к2
Р + АР кхР
_ а+(р + у)Р , _
1 аР ’ ~
Р + АР
(Р + У )Р+-
Значения Р, П, Ф и О указаны на рис. 1.2, а коэффициенты приоритетности - на рис.
1.3 и в табл. 2.1.
Если а = 0,7; р + у = 0,3; Р = 0,22; АР = 0,1; П = 510; Д = Ф + О = = 2295, то кх - 1,4;к2 = 1,04; П + АП - 1\А\Д- АД = 2206,7.
| Таблица 2.1 Коэффициенты относительной важности аргументов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ф + АФ = кхФ,
ро
Р0+уФ-
0(у + р)
кх -¦
у(Д-АД)-$0-уФ
уф
Если Р = 0,1; у = 0,2; Ф = 2000, О = 295, то получим: кх = 1,044; к2 = 2,49; Ф + ДФ= 2088; 0-АО= 120,4.
Проверка. Д - АД = 2088 + 120,4 = 2208,4 2206,7.
у + Х у+Х
Проверка. Р + АР =
П+АП
д-ьд
0,32.
Здесь индивидуальные коэффициенты равны:
7777 + А7777 = 7777,
ПД + ШД = к2ПД,
, 77 + А77 - к2ПД + 77 ,
1 ял 2
П + АП + Н-ПП + -ПД
_р
ПД(^+1)
Если а = 0,9; р = 0,1; П = 714; ПП = 400; ПД = 120; Я = 10, то получим: = 1,46; к2 = 1,17; ЛЯ + ДЯЛ= 584; ПД + АПД= 140,4. Проверка. П + АП = 584 + 140,4 - 10 = 714,4 = 714.
З.ЛЛ+ =В+(а)-С"(Р);
Индивидуальные коэффициенты равны:
В + АВ = кД,
ЛЛ + ДЛЛ +
*.=-
С( +1)
р
-С-ПП-АПП+В
Р
Так как а = 0,6; Р = 0,4; 5 = 4000; С = 3600, то получим: кх = 1,03; /t2 = 1,02; В + АВ = 4080; С - АС = 3495,12.
Проверка. ПП + ДЛЯ = 4080 - 3495,12 = 584,8.
4.В+ = К+(а)Ц-ф).
Индивидуальные коэффициенты равны:
К + АК = к]К, Ц-АЦ =
(В + АВ)к2 КЦ
-Ц + К +
Р
(-Ц + К)2-4-(КЦ + АВ)
Так как а = 0,7; Р = 0,3; К = 200; Ц = 20, то получим: к1 = 1,545; к2 = 1,5; К + АК = Ш;Ц-АЦ= 13,3.
Проверка. В + АВ = 309 - 13,3 = 4109,7 4080.
5. С = ПЕР+ (а) + ПОСТ (Р).
Рассчитаем коэффициенты:
ПЕР + АПЕР = к\ ПЕР,
ПОСТ
ПОСТ - АПОСТ = ,
к2
оПОСТ - а (С - АС) + рДЕР 1_ ф-а)ПЕР ’
ПОСТ
1 ~ С АС +
(р-а)
Так как ПЕР = 2100; ПОСТ = 1500; а = 0,3; |3 = 0,7, то получим: * = 1,04; *2=1,15; ПЕР + ДЯ?Р = 2184; ПОСТ- АПОСТ = = 1304,3.
Проверка. С-АС = 2184 + 1304,3 = 3488,3 * 3495.
6. /7?Р~ = К ¦ ПЕ+ (а), а = 1.
Здесь мы имеем функцию с одной переменной, которая обратима. Поэтому обратные вычисления не нужны. Прирост для одного аргумента равен:
ПЕР + АПЕР = (ПЕ + ДПЕ)К,
2184
13,3
ПЕР+АПЕР К
ПЕ + АПЕ
164,2.
Результат: ПЕ + А ПЕ = 164,2.
7. ПЕ+ = ПРП+ (а) + НПР+ (Р).
Здесь мы имеем аддитивную функцию, поэтому задачу можно решить путем пропорционального деления прироста функции. Так как а = 0,2; |3 = 0,8; ДПЕ = 59,4, то получим:
ПРП + А ПРП = ПРП + аД ПЕ = 60 + 0,2 - 59,4 = 71,88;
НПР + ДНПР = НПР + РДЯ? = 45 + 0,8 - 59,4 = 95,52. Проверка. ПЕ + АЛЕ = 164 164,2.
8. ПРП* = ПМЗ* (а) + ПЗТ+ (р) + ПР\+ (у).
Здесь так же, как и в формуле пункта 7 имеем аддитивную функцию, поэтому при а = 0,5; Р = 0,3; у = 0,3; ЫІРП = 11,88 получим:
ПМЗ + ЬЛМЗ = ПМЗ + а - Д ПРП = 25,94;
ПЗТ + АПЗТ = ПЗТ + Р - ЛПРП = 33,56;
ПР\ + Д77Р1 = 7ZP1+у - АПРП = 12,4.
Проверка. ПРП + ЫІРП = 71,87.
9. НПР+ = АУЦ+(а) + РЕМ* (Р) + ПР2* (у).
Здесь так же, как и в формулах пунктов 7 и 8, можно воспользоваться пропорциональным делением прироста функции. При а = 0,4; Р = 0,4; у = 0,2; ДНПР = 50,52 получим:
АУЦ + ААУЦ = АУЦ + а-АНПР = 32,2;
РЕМ + АРЕМ = РЕМ + Р - АПРП = 33,2;
ПР2 + АПР2 = ПР2 + а - А ПРП = 30,1.
Проверка. НПР + ДНПР = 95,5 * 95,52.
Ю.ПОСТ- =РУ-(а) + ОХ'ф) +АП'(у)+ ПРЗ~ (о).
Для решения данной задачи следует воспользоваться процедурой свертки/развертки. Обозначим через РУ + ОХ = А и АП + + ПРЗ = В. Тогда имеем:
ПОСТ- = Л(а + р) + Д-(у + о).
Введем индивидуальные коэффициенты:
А-АА = ,
А
5-Д5 = ,
к2
к- ±
1 (у + а)А - (а + р)Я + (а + р)(ПОСТ - АПОСТ) ’
*2=_I_
ПОСТ-АПОСТ- к\
Первый промежуточный результат: , = 1,12; 2 = 1,18; Л - ДЛ 625; В-АВ = 677,96.
А~ =Ру-(а') + ОХ-ф'); а'= 0,6; р' = 0,4;
РУ_
к\ ’ ОХ
РУ-АРУ=
ОХ-АОХ
аг
РУ
к\ =
р'РУ-ат + а?-АЛ)’ 2 А_М_РУ_
При РУ = 300; ОХ = 400; а = 0,3; Р = 0,2 получим: кх = 1,18, к2 = 1,08; РУ- АРУ = 254,24; ОХ-АОХ= 370,4.
Проверка. А - АА = 254,24 + 374,4 = 624,6 = 625.
В' = АП’(у')+ ПР4~(o'); у' = 0,4; о' = 0,6;
АП
к ;
ПР4
АП - ААП =
ПР4-АПР4 =
ЛЯ
к\ =
а'ЛЯ - у'ПР4 + у\В - АВ) ПР4
к2 - -
АП‘
В-АВ-
При ЛЯ = 100; ЯР4 = 700; у = 0,2; а = 0,3 получим следующее: кх = 1,95, к2 =1,12; АП - ААП = 51,28; ЯРЗ - АЯРЗ = 625. Проверка. В -АВ = 51,28 + 625 = 676,28 677,9.
11.Ф+ = АФ+(а) + Пф-($). Введем индивидуальные коэффициенты:
АФ + ААФ = к,АФ;
ПФ
ПФ-АПФ =
* =
аПФ - а(Ф + ДФ) + РАФ ~ АФф-а) ’
к Пф
2~ Ф + АФ-кхАФ'
При а = 0,6; Р = 0,4; АФ = 900; ПФ =1100 получим: кх = 1,29, к2 = \,\9;АФ-ААФ = 1161; ПФ- АПФ = 924,4.
Проверка: Ф + АФ = 1161 + 924,4 = 2085,4 = 2088.
12.0' = П3~ (а) + ЯГ (р) + ГП~ (у) + ДС~ (X) + ПР4~ (а).
Здесь функция имеет пять аргументов, что сущуственно затрудняет возможность установить приоритетность аргументов. Поэтому откажемся от весов важности целей и решим задачу без них:
Л . у*. ПЗ НЗ ГП ДС ПР4
О-АО- + + + -!= +-.
X X X X X
Отсюда получим:
= 2,45.
О-АО
Результат: ПЗ - АПЗ = 57,14; НЗ - А НЗ = 18,37; ГП - А ГП = = 22,45; ДС-АДС = 16,33; ПР4 - АПР4 = 6,12.
Проверка. О-ДО = 57,14 + 18,37 + 22,45 + 16,33 + 6,12 = 120,4.
\Ъ.ПЗ~ =ТЗ-(а)+ СЗ~ф) + ПД 4-(у).
Здесь можно применить единый коэффициент, согласно которому будут снижаться приросты:
АТЗ = а к0; АСЗ = р Л0; АПД = у-к0; ПЗ-АПЗ = ТЗ-ак0 +СЗ-рХ0 + ПД4-у-к0.
Отсюда получим: к0 = АПЗ.
При а = 0,6; р = 0,3; у = 0,1; АПЗ = 82,86; ТЗ = 100; СЗ = 25; ПД4 = 15 получим: АТЗ = 49,7; АСЗ = 24,9; АПД4 = 8,28.
Результат: ТЗ-АТЗ = 50,3; СЗ - АСЗ = 0,1; ПД4 - АПД4 = 6,72. Проверка. ПЗ - АПЗ = 57,12 57,14.
14. ДС~ = СС~ (а) + ЗС~ (Р).
СС
СС+АСС=
зс
ЗС-АЗС = ;
СС
*і =
рсс - аЗС + а (ДС - АДС) ЗС
кг =¦
СС'
ДС-АДС-
При а = 0,1; р = 0,9; СС = 15; ЗС = 25 получим: к= 1,19; к2 = = 6,67; СС - А СС = 12,6; ЗС - АЗС = 3,73.
Проверка. ДС - АДС = 16,33.
| Таблица 2.2 Результаты обратных вычислений с учетом имеющихся ресурсов, руб. |
||||||||||||||||||||||||||||
|
| Показатель | Значение | |
| предыдущее | новое | |
| Затраты на оплату труда работников | зоо | 254,24 |
| управления | ||
| Затраты на охрану | 400 | 370,40 |
| Арендная плата | 100 | 51,28 |
| Прочие постоянные затраты | 700 | 625,00 |
| Активная часть основных фондов | 900 | 1161,00 |
| Пассивная часть основных фондов | 1100 | 924,40 |
| Производственные запасы | 140 | 57,14 |
| Незавершенное производство | 45 | 18,37 |
| Готовая продукция | 55 | 22,45 |
| Денежные средства | 40 | 16,33 |
| Прочие элементы оборотного капитала | 15 | 6,12 |
| Текущий запас | 100 | 50,30 |
| Страховой запас | 25 | 0,10 |
| Подготовительный запас | 15 | 6,72 |
| Собственные денежные средства | 15 | 12,60 |
| Заемные средства | 25 | 3,73 |
Она может служить основой для разработки планов мероприятий, необходимых для функционирования различных структурных подразделений, ответственных за достижение того или иного показателя.
Очевидно, изменение показателей наталкивается на ограничения, ибо ресурсы предприятия всегда конечны. Поэтому необходим алгоритм, с помощью которого можно определить прирост одного показателя за счет другого.
Как этого можно достичь, будет показано в гл. 6.
Глава 3ПРИМЕНЕНИЕ ОБРАТНЫХ ВЫЧИСЛЕНИЙ ДЛЯ ФОРМИРОВАНИЯ РЕШЕНИЙ В УСЛОВИЯХ РИСКА
Дерево вероятностей
Существует большое число задач, где зависимости между переменными носят вероятностный характер. Среди таких задач достаточно актуальными являются:
- управление рисками - определение условий (мероприятий, состава объектов, параметров, характеристик и т.д.), гарантирующих снижение финансовых, инвестиционных, банковских, информационных и других рисков до желаемого уровня;
- управление безопасностью - определение условий или мероприятий, выполнение которых обеспечит установленный уровень информационной, экономической, технической, экологической, военной, социальной и др. безопасности;
- управление надежностью - определение условий, гарантирующих установленный уровень надежности системы (информационной, экономической, технологической).
Решение перечисленных задач предполагает наличие у лица, принимающего решение, соответствующего аппарата, способного ответить на вопрос: Что делать?. Например, лицу, формирующему решение, необходимо знать ответ на вопрос: Каковы должны быть условия для того, чтобы уровень инвестиционного риска снизился с 0,6 до 0,2?.
Чтобы система могла выдавать ответы на такого рода вопросы, необходимо поставить и решить обратную по отношению к прямой задачу, которая может, например, формироваться следующим образом: От каких факторов зависит инвестиционный риск и как он определяется?.
Так же, как и в детерминированных задачах, одни вероятностные события зависят от других событий, которые, в свою очередь, могут носить как детерминированный, так и стохастических характер. Поэтому в общем случае следует рассматривать зависимости и того, и другого характера совместно.
Проблема решения обратных задач на основе обратных вычислений, сочетающих в себе детерминированные и вероятностные задачи, еще ждет своего решения. Пока мы остановимся лишь на методах решения обратных вероятностных задач.
Вероятностные зависимости одних событий от других будем представлять с помощью графа, который, как правило, вырождается в дерево. Далее такое дерево будет называться деревом вероятностей. В узлах дерева будут находиться вероятности наступления тех или иных событий, а дуги будут символизировать связи между событиями.
Все узлы будут делиться на две группы: расчетные и терминальные. Значения вероятностей событий, находящихся в терминальных узлах, либо заданы, либо определяются правилами, находящимися вне обратных вычислений. Расчетные узлы - это результат обратных вычислений.
Корень дерева - это узел, где указывается значение вероятности, заданное лицом, формирующим решение (желаемый уровень риска, надежности, безопасности и т.п.).
На рис 3.1 представлено дерево, иллюстрирующее в общем виде прямые и обратные вероятностные вычисления.
Направленность дуг указывает на различие используемой исходной информации. Дуги, направленные вверх, указывают на прямые вероятностные вычисления.
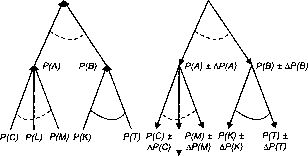
Для них в качестве исходной информации выступают вероятности терминальных узлов дерева. Если же дуги направлены вниз, то мы имеем дело с обратными вычислениями, для которых часть исходной информации находится в корне дерева.
Кроме того, линии на рис. 3.1, которые связывают события, являются либо пунктирными, либо сплошными дугами: пунктирная символизирует операцию сложения вероятностей, сплошная -операцию умножения.
На рис. 3.1,6 к вероятности наступления событий А или В (Р(Л + В)) добавлен прирост АР(А + В), который совместно с дополнительными данными служит исходной информацией для расчета приростов всех оставшихся узлов дерева.
Буквами греческого алфавита (а, (3, у,...) обозначены коэффициенты приоритетности наступления тех или иных событий, а с помощью знаков плюс или минус - направления приростов этих изменений. Например, Р(А) + АР(А) указывает на рост вероятности Р(А) на величину АР{А), а Р{В) - АР{В) отражает уменьшение вероятности Р(В) на величину АР(В).
Большинство модификаций метода обратных вычислений, рассмотренных в гл. 2, применимы и для решения вероятностных задач. Рассмотрим две модификации:
- решение задач обратных вычислений без коэффициентов прироста аргументов;
- то же без указания приоритетов целей.
Задачу обратных вероятностных вычислений в общем виде можно сформулировать следующим образом:
известны: вероятность наступления событий А, В, С, ...;
формулы, по которым вычисляются вероятности наступления событий А, В, С,...;
желаемый прирост вероятности наступления события, отражаемого в корне дерева вероятностей;
желаемые направления приростов изменении вероятностей в узлах дерева;
приоритетность в изменении наступления событий;
определить: новые значения вероятностей наступления событий, отражаемых терминальными узлами дерева;
соотношение условий, обеспечивающих новые значения вероятностей в терминальных вершинах. ,
Далее рассмотрим формальные постановки обратных вероятностных задач и их решения с помощью обратных вычислений для следующих классов вероятностей:
- Безусловная вероятность наступления одного из несовместных событий.
- Безусловная вероятность наступления одного из совместных событий.
- Условная вероятность совместного наступления событий.
- Условная вероятность совместного наступления независимых событий.
- Вероятность наступления события совместно с одним из ряда несовместных событий (полная вероятность).
- Вероятность, характеризуемая функцией или плотностью распределения.
- Вероятность появления события в некоторой серии испытаний (формула Бернулли).
Рассмотрим постановки задач в двух вариантах, а также примеры их решения. В стремлении к простоте изложения в примерах участвуют лишь два события (А и В).
3.2.Поиск безусловной вероятностинаступления одногоиз несовместных событий
Решение задачи без коэффициентов прироста
Как известно, вероятность наступления в некотором испытании какого-либо одного из событий А, В, С,... равна сумме вероятностей событий, если любые два из них несовместны. Расчет ведется по формуле
Р(А + В + С+ ...) = Р(А) + Р(В) + Р{С) +....
Дальнейшее чтение материала предполагает предварительное ознакомление с разд. 2.3.
В общем виде задача обратных вычислений, если рассматриваются два события, решается с помощью следующей системы уравнений:
Р(А + В) ± АР(А + В) = Р(А) ± АР(А) + Р(В) ± АР(В),
АР(А) _ а АР(Я) "(3’
где Р(А + В) -вероятность наступления одного из независимых
событий А или 2?;
± АР(А + В) - желаемый прирост вероятности наступления одного
из независимых событий А или В\
Р(А), Р{В) - вероятности наступления событий А и В соответ
ственно;
± АР(А), ± АР(В) - приросты вероятностей наступления независимых событий А и В соответственно;
а, (3 - коэффициенты приоритетности в наступлении собы
тий А и В соответственно.
1. Целевая установка: Р(А + В)* = Р(А(о))+ + /*(ЖР))+.
Задача обратных вероятностных вычислений принимает вид:
Р(А + В) + ЛР(А + В) = Р(А) + АР(А) + Р(В) + АР(В),
АР(А) а АР(В)~ р'
Как и ранее, а + (3 = 1.
Полученные в результате решения новые вероятности наступления событий А и В позволяют определить новые условия, от которых они зависят. Если через Xt обозначить новые условия для свершения события А, а через Х2 - для события В, то мы приходим к двум уравнениям:
Р{А) + ЬР(А) =
п
Р(В) + АР(В) =
где п - общие условия наступления событий А и В.
Ответ будет следующим:
*,=п(/(Л)±ДР(Л));
Х2=п(Р(В)±АР(В)).
п р и м е р (рис. 3.2).
Рассматривается урна, в которой находятся три красных шара, четыре белых и четыре черных. Вероятность того, что при одном извлечении будет вынут либо красный, либо белый шар без труда можно определить по формуле безусловной вероятности. Обозначив через А событие извлечения красного шара, а через В - белого, получим:
Р(А + В) = Р(А) + Р(В) = + = = 0,63.
11 11 11
На рис. 3.2, а графически представлено прямое вычисление вероятностей наступления двух независимых событий А или В, а на рис.
3.2, б- обратные вероятностные вычисления с одинаковой направленностью в изменении аргументов.
Пунктирная дуга, соединяющая дуги графа, указывает на то, что речь идет о появлении либо события А, либо события В.
Допустим, необходимо увеличить вероятность наступления событий А или В до 0,8. На рис.
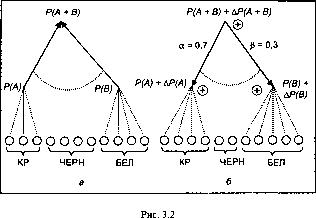
3.2, 6 показаны в окружностях знаки плюс, означающие, что как вероятность (Р(А)+АР(А)) наступления события А, так и вероятность (Р(В)+АР(В)) наступления события В должны увеличиваться. Достижение цели, заключающейся в повышении вероятности наступления независимых событий Aw В, должно в большей части происходить за счет повышения вероятности наступления события А. Это отражает коэффициент приоритетности а = 0,7.
В меньшей мере нагрузка ложится на второе событие В. Коэффициент приоритетности его наступления равен 0,3.
Для решения сформулированной задачи обратных вычислений запишем следующую систему уравнений:
Р(А + В) + АР(А + В) = Р(А) + АР(А) + Р(В) + АР(В),
АР(А) __ а АР(В) ~ (3
Так как желаемое значение вероятности наступления событий А или В известно из условия задачи (Р(А + В) + АР(А + В) = = 0,8), а существующая вероятность равна 0,63, то, подставив эти значения в приведенную систему уравнений, получим:
0,17 = АР(А) + АР(В),
АР(А) 0,7 АР(В) _ 0,3
Решая эту систему, имеем:
АР(А) = 0,11,
АР(В) = 0,05.
Таким образом, новые значения вероятностей наступления событий Л или В равны:
Р(А) + АР(А) = 0,27 + 0,11 = 0,38;
Р(В) + АР(В) = 0,36 + 0,05 = 0,41.
Для того чтобы обеспечить новые условия для наступления событий А или В, решим следующие уравнения:
Р(Л) + ДР(Л) = ^-;
п
Р(5) + Д/(Я) = ,
П
где Ху Х2 - число красных и белых шаров, обеспечивающих новую вероятность наступление событий А или В, являющихся независимыми.
