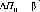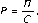Решение задач без коэффициентов прироста аргументов
Пусть, как и ранее, задана функция у = f(x, z). Введем величину к0, которая, будучи умноженной на КОВ каждого из аргументов, позволит получить желаемый для них прирост.
8. Целевая установка: у+ = /(jc+(a), г+(р)).
Введем единую величину к0 и получим искомые приросты следующим образом:
Ах = a - к0,
Az = p-?0.
Задача обратных вычислений заключается в поиске величины к0 из уравнения
у + Ау = /О + akQ, z + р0).
Пр и мер (рис. 2.8).
Умножением количества на цену получают выручку, приобретенную в результате реализации продукции. Формула расчета имеет вид:
Р = КЦ,
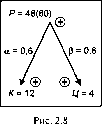
Допустим, целевая установка следующая: нарастить выручку за счет увеличения количества продаваемой продукции и ее цены. При этом большая часть выручки должна быть получена за счет увеличения количества (а (3). Такая установка отразится следующим образом:
Р+ = К+ (а) ¦ Ц+ (3), a р.
Введем величину к0 и получим:
АК = а к0; АЦ = (3 к0;
Р + АР = (/Г + аА0)(Л + РА0);
; _ -(аЦ + ptf) ± 7(аД + РА-)2 + 4ард/
~ 2ар '
Вполне очевидным ограничением на исходные данные служит следующее неравенство:
УІІаЦ + рК)2 +4фАР -(аЦ + рЯ-)-
Проверка, а = 0,6; Р = 0,4; К = 12; Ц = 4; Р = 48; Д/' = 12; 0 = 1,58; ДАТ = 0,6 -1,58 = 0,95; АЦ = 0,4 - 1,58 = 0,63;
К + АК= 12 + 0,95 = 12,95; Ц + АЦ = 4 + 0,63 = 4,63;
Р + АР = 12,95 - 4,63 = 59,958 = 60.
9. Целевая установка: /* = /(х+(а), z (Р)).
Задача заключается в поиске величины к0 из следующего уравнения:
у + Ау = f(x + ak0, z -р?0).
Пример. Воспользуемся примером из целевой установки 2, имеющей вид
П+( а)
С~(Р) ’
Р+
ар,
где Р - рентабельность;
П - прибыль;
С - себестоимость продукции.
Введем величину к0 и получим:
А/7 = ак0; А С = Р к0;
П + ак0
С-рЛо ;
к0 =
АPC
Р(Р + АР) + а
Проверка, а - 0,7; (3 = 0,3; П = 24; С = 4; Р = 6; АР = 4; 0 = 4,32; АЯ = 0,7 - 4,32 = 3,02; АС = 0,3 - 4,32 = 1,3; Я + АЯ = 27,02;
27 02
С-АС = 2,7; Р + АР = і= 10.
2,7
10. Целевая установка: = f(x~(а), г+(Р)).
В общем виде задача запишется следующим образом:
y + Ay = f(x-ak0,z + р*о).
Пример (рис. 2.9). Обратимся к задаче из целевой установки 3, где речь шла о среднегодовой стоимости основных производственных фондов Ф, которая рассчитывалась по формуле
Ф = АФ + ПФ,
где АФ - среднегодовая стоимость активной части основных производственных фондов;
ПФ - среднегодовая стоимость пассивной части основных производственных фондов.
Как и ранее, будем считать, что необходимо нарастить среднегодовую стоимость основных производственных фондов за счет снижения АФ и повышения ПФ. Прирост следует добиться большей частью за счет увеличения ПФ.
Это отражается в формуле расчета следующим образом:
Ф+ = А Ф~ (а) + ПФ+ (Р), р а.
Введем величину к0 и получим:
АФ
ААФ = ак0; АПФ = р?0; АФ = 0(а-Р); к0
Р~а
Проверка, а = 0,4; (3 = 0,6; АФ 40; ПФ = 10; Ф = 50; АФ = 2; kQ= 10; ААФ = 4; А ПФ = 6; АФ - ААФ = 36; ПФ + АЯФ = 16; Ф + АФ = 36 + 16 = 52.
11. Целевая установка: д;+=/(л: (а), г (Р)).
В общем виде задача запишется так:
у + Ау = f(x-ak0, z -р?0).
Пример. Вернемся к целевой установке 9 и рассмотрим, можно ли решить задачу повышения рентабельности путем одновременного уменьшения прибыли и себестоимости продукции с помощью единого коэффициента. Тогда целевая установка запишется следующим образом:
, + = 1Г(а)
С(Р) ’
где Р - рентабельность;
П - прибыль;
С - себестоимость продукции.
Как и ранее, введем величину к0 и получим:
АП = ак0; АС = рк0;
Р + АР =
П -ак0
с-рк0 ’
С-АР
0 " Р(Р + ДР)-сГ
Проверка, а = 0,7; Р = 0,3; П = 24; С = 4; Р = 6; ДР = 4; 0 = 6,96; ДЯ = 0,7 - 6,96 = 4,87; АС = 0,3 - 6,96 = 2,09; Я - ДЯ = 24 - 4,87 =
= 19,13; С - АС = 4 - 2,09 = 1,91; Р + ДР = ^^ = 10,015 * 10.... ,91
Теперь рассмотрим случаи снижения значения функции.
12. Целевая установка: у = /(л:+(а), г+(Р)).
В'общем виде задача запишется так:
у Ау = f(x + ct0, z + р0 ).
Пример (рис. 2.10). Воспользуемся примером из целевой установки 1, в котором прибыль П определяется путем вычитания себестоимости продукции С из выручки В:
П = В-С.
Изменив знак прироста функции, получим следующую целевую установку:
П~ = В+ (а) - С+ (Р).
Решая уравнение
А-АА = (B + ak0)-(C + fik0), где
- АВ = ак0, АС = fik0,
получим
0 р-а
Проверка, а = 0,3; (3 = 0,7; В = 12; С = 4; П = 8; ДП = 2; к0 = 5; ДД = 0,3 - 5 = 1,5; АС = 0,7 - 5 = 3,5; Я- ДЯ = (12 + 1,5) - (4 + 3,5) = 6.
13. Целевая установка: у = f(x (а), г+(Р)).
В общем виде задача запишется так:
У ~ Ay = f(x-ак0, z + Р?0).
Пример (рис. 2.11). Обратимся к примеру, рассмотренному в целевой установке 2. Однако теперь зададимся иной целью, которая будет заключаться в понижении рентабельности за счет уменьшения прибыли и повышения себестоимости.
Большая часть прироста должна быть обеспечена за счет уменьшения прибыли. Такая целевая установка запишется следующим образом:
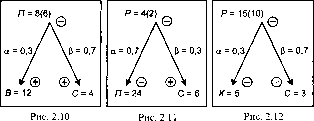
а р.
Р- . П~(а)
С+(р)’
Решив уравнение относительно к0, получим:
П-С(Р-АА) р(Р-АР) + а *
Проверка, а = 0,7; р = 0,3; П = 24; С = 6; Р = 4; АР = 2; 0 = 9,23;
14. Целевая установка: у = /(* (а), г О.
В общем виде задача запишется так:
y-ky = f(x-ak0,z-$k0).
Пример (рис. 2.12). Затраты на перевозку продукции рассчитываются по формуле:
Р = КС,
где Р - затраты на перевозку;
К - количество перевозимой продукции;
С - стоимость перевозки единицы продукции.
Допустим, целевая установка следующая: снизить затраты на перевозку за счет снижения количества перевозимой продукции и стоимости перевозки единицы продукции. Большая часть снижения затрат должна произойти за счет снижения количества продукции. Такая целевая установка отразиться следующим образом:
Р~ - (а) - (Р).
Введем величину kQ. Тогда задача обратных вычислений запишется в виде:
откуда получим:
Проверка, а = 0,3; р = 0,7; К= 5; С = 3; Р = 15; АР = 5; к0 = 1,21; Р- АР = (5-0,3* 1,21)(3 - 0,7 - 1,21) = 9,967 * 10.
Иногда у пользователя при наличии функции, с числом аргументов больше двух нет желания применять процедуру свертки/
развертки. В этом случае лицо, формирующее решение, сталкивается с проблемой решения уравнений п-й степени.
Если такая перспектива для него приемлема, то процесс расчетов сокращается.
Пример. Численность вспомогательных рабочих Ч определяется по формуле
Ч=М-С-К9
где М - число мест вспомогательных рабочих;
С - количество рабочих смен;
К - коэффициент списочного состава.
Необходимо за счет увеличения всех аргументов повысить численность вспомогательного состава. Такая целевая установка отразится следующим образом:
Ч+ =М+(а). С+Ф)К+(у).
Если, как и ранее, ввести величину kQ, то можно получить:
АМ = ак0; АС = р0; АК = ук0.
Это позволяет записать задачу в виде:
Ч +АЧ =(М + ак0)(С- р к0 )(К + ук0).
Отсюда получим:
a|Jy/to + ap/^o + (аСК+рМК + у СМ + ауС + руМ)к0-АЧ =0.
Решить это уравнение можно с помощью метода Кардано.
Подобным образом можно вывести уравнения для любого числа аргументов, что, однако, вынуждает прибегать к численным решениям уравнений высших порядков.
Решение задач без коэффициентов прироста аргументов
Пусть задана функция у = f(x, z). Целевые установки, учитывающие пожелания пользователя, остаются прежними.
Вначале рассмотрим варианты, учитывающие увеличение функции, а затем ее снижение.
Гу + Ау = /(jc + Ajc, z + Az),
Ах _ а Az Р
В такой постановке надлежит пользоваться следующими ограничениями:
Ах 0, Az 0.
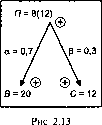
Пример (рис. 2.13). Воспользуемся зависимостью из целевой установки 1, где фигурируют прибыль Я, выручка В и себестоимость продукции С. Эта зависимость представляется в виде формулы
Я = Д-С.
Целевая установка состоит в следующем: необходимо нарастить прибыль за счет повышения выручки и себестоимости, причем большая часть прироста прибыли должна произойти за счет повышения прибыли, а меньшая - за счет повышения себестоимости. Такая целевая установка отражается следующим образом:
П+ =Я+(а)-С+(Р), ар.
Представим эту задачу в виде системы уравнений:
П + АП = В + АВ-(С- ДС),
' АД _ а АС _ Р
Решив ее относительно А В и АС, получим:
АВ = АС,
Р
Проверка, а - 0,7; Р = 0,3; В = 20; С = 12; П = 8; АЯ = 4; АС = 3; АД = 7;Д + АВ = 27; С + АС = 15; П + АЯ = 27 - 15 = 12.
Какими граничными значениями должны обладать Ду, а и Р, чтобы задача имела решение, укажет система следующих неравенств:
Одним из очевидных ограничений является неравенство
ар.
В качестве примера здесь использована аддитивная функция, для которой отыскивались приросты с одинаковыми знаками. В п. 1.3 было показано, что в таких частных случаях задачу можно решить путем пропорционального деления прироста функции и добавления результатов деления к ее аргументам.
Этого не сделано с целью демонстрации общности метода обратных вычислений без коэффициентов прироста аргументов.
у + Ау = f(x + Ах, z - Az),
Ах_а Az Р
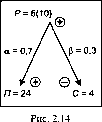
Пример (рис. 2.14).
Воспользуемся примером из целевой установки 2, в которой рентабельность Р рассчитывается делением прибыли П на себестоимость продукции С. Пусть целевая установка остается прежней, т.е. необходимо увеличить рентабельность за счет повышения прибыли и снижения себестоимости, причем большая часть увеличения рентабельности должна произойти за счет повышения прибыли, а меньшая - за счет снижения себестоимости. Такая целевая установка представляется следующим образом:
Я+( а)
С~(Р) ’
Р+
ар.
Составим систему уравнений:
П + АП С-АС’
Р + АР--АП а
АС р
Решив ее относительно АП и АС, получим:
(Р + АР)С-П Р+АР+-
Р
а АС
Р '
АП =
Неравенствами для поиска приемлемых диапазонов исходных данных служат выражения: АС 0 и АП 0.
Проверка. а = 0,7; Р = 0,3; П = 24; С = 4; Р = 6; АР = 4; АС = 1,3;
27
ДЯ= 3;Я + АП = 21; С + АС = 2,1; P + bP = s‘10’
у + Ay = f(x- Ах, z + Az), Ах а
Пр и мер (рис. 2.15). Прибыль 77 , направляемая на потребление, и прибыль 77 , направляемая на инвестиции, составляют общую прибыль, равную
П Пп + Пи,
где П - общая прибыль.
Необходимо определить, какими должны быть величины Пп и 77 , чтобы П увеличилась на величину А/7. Прибыль Пп должна снизиться, а прибыль Яи - увеличиться.
Большая часть А/7 должна возникнуть за счет увеличения 77и, а меньшая - за счет 77п. Такая целевая установка отражается следующим образом:
7/+ = /7" (а) + П+ (р), а р.

Рис. 2.16
Представим эту задачу в виде системы уравнений:
П + АП = (77п - А/7П) + (77и + А/7И), ДЯП _а
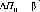
Решив ее, получим:
А „ а А „
АЯП = АПи,
АЯИ=.
Р
Очевидным ограничением служит выражение а р. Проверка, а - 0,3; Р = 0,7; Яп - 10; Яи = 30; П - 40; ДП 7; ДЯп = 5,26; ДЯи = 12,28; Яп - ДЯп = 10 - 5,26 = 4,74; Яи + ДЯи = = 35 + 12,28 = 42,28; Л + АП = 4,74 + 42,28 = 47,02 47."
18. Целевая установка: у+ = f(x~(a), г~(Р.
Задача обратных вычислений принимает вид:
У + Ay = f(x - Ах, z - Az%
^ Ах а
Az р
Как правило, Задача имеет решение при а р.
Пример (рис. 2.16). Индекс прибыли рассчитывается по формуле
Б_ А’
где / - индекс прибыли;
Б - прибыль базового периода;
А - прибыль анализируемого периода.
Необходимо поднять индекс за счет снижения прибыли как в базовом, так и в анализируемом периодах. Большая часть снижения должна произойти за счет снижения прибыли в анализируемом периоде. Такая целевая установка отразится следующим образом:
/+ _ Б (а)
А ФУ
Запишем систему уравнений:
Б-АБ А-АА 9
/ + Д/ = АБ а
АА Р
Решив данную систему, получим:
А(І + АІ) - Б
т at а ’
/4-Д/--
АБ = АА.
АЛ -
Проверка. Б = 20; А = 15; / = 1,3; АІ = 0,17; а = 0,3; |3 = 0,7; АА = 2,31; АБ = 0,99; Б - АБ = 20-0,989 = 19,01; Л - АА = 15--2,31 = 12,69; І + АІ = = 1,498*1,5.
12,69
Теперь рассмотрим задачи, решение которых позволяет снизить значение функции.
19. Целевая установка: j; = f(x+(a), г+(Р)).
Задача обратных вычислений принимает вид:
у - Ay = f(x + Ах, z + Az),
- Ах _ а Az Р
Пр и мер (рис. 2.17). Воспользуемся зависимостью из целевой установки 1, где прибыль П рассчитывается на основе выручки В и себестоимости продукции С. Расчет выполняется по формуле
П = В-С.
Целевая установка состоит в следующем: необходимо снизить прибыль, однако выручка и себестоимость должны повыситься. При этом большая часть снижения прибыли должна произойти за счет повышения себестоимости. Такая целевая установка отражается следующим образом:
П~ = В+ (а) - С+ (Р), р а.

Составим систему уравнений:
77 - АП = В + АВ - (С - АС),
АВ а
дсТ
Решив ее относительно А В и АС, получим:
АВ = , АС = .
Р 1_"
Ограничением служит выражение ^ * ¦
Проверка, а = 0,3; Р = 0,7; В = 20; С = 12; 77 = 8; Д77 = 4; АС = 7; АВ = 2,99; В + АВ = 22,99; С + АС = 19; П-АП = 22,99 - 19 = 3,99 - 4.
20. Целевая установка: у~ = f(x+(a), г-(Р)).
Задача обратных вычислений принимает вид:
ry-Ay = f(x + Ax,z-Az),
Ах _ а Az р
Пример (рис. 2.18). Прибыль Пп, направляемая на потребление, и прибыль 77и, направляемая на инвестиции, составляют общую прибыль П, равную
П ~ Пп Л„.
Целевая установка следующая: необходимо снизить общую сумму прибыли, причем большая часть отрицательного прироста прибыли должна быть обеспечена за счет увеличения прибыли, направляемой на потребление, и меньшей - за счет прибыли, направляемой на инвестиции. Такая целевая установка запишется следующим образом:
Л- = Лп+(х) + /7и(р).
Это позволяет сформулировать следующую задачу обратных вычислений:
П - А/7 = Пп+ А/7П + (77и - А/7И), ЛЯ^=а АЯИ р'
Решив ее, получим:
АЯ„
АЯИ
АЯИ
Р ’
Д/7
Ограничением служит выражение а р.
Проверка, а = 0,3; Р = 0,7; Пп = 12; 77и 8; П = 20; Д/7 = 2; АП = 3,5; ДЯ = 1,5; П + АП =12+ 1,5 = 13,5; П - АП = 8 -- 3,5 = 4,5; П - АП = 13,5 + 4,5 = 18.
21. Целевая установка: у = /(* (а), г+(Р.
Запишем задачу обратных точечных вычислений:
у - Лу = f(x Ах, z + Az), s Ах: _ а Az р
Пример (рис. 2.19).
Воспользуемся целевой установкой 20, но изменим знак первого аргумента на минус, а второго - на плюс. Кроме того, большая часть отрицательного прироста функции должна быть получена за счет первого аргумента. Такая целевая установка запишется следующим образом:
П~ = П~ (а) + П* (Р).
Задача обратных вычислений примет вид:
П - АП = Пп -АПа + (Яи + АЯи),
АПп _ а
¦ лдГр'
Решив ее, получим:
ЛЯП
АЯИ
аЛЯи
~Г~’
АП
Ограничением служит выражение: а р.

Проверка, а = 0,7; Р = 0,3; Пп = 12; Пк = 8; П = 20; ДЯ = 2; ДЯ = 1,5; АП = 3,49; Я - ДЯ = 12 - 3,49 = 8,51; Я + ДЯ =
и’’п’’п п ’ ’’и и
= 8 + 1,5 = 9,5; Я- ДЯ = 8,51 + 9,5 = 18,01 - 18.
22. Целевая установка: у = f(x (a), z (Р)).
Задача обратных вычислений в данном случае имеет вид:
у - Ay = /(х- Ах, z - Az),
Ах _ а Az Р
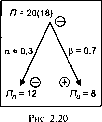
Пример (рис. 2.20). Воспользуемся примером из целевой установки 20, но изменим знак обоих аргументов на минус.
Кроме того, будем считать, что большая часть отрицательного прироста функции должна быть получена за счет второго аргумента. Такая целевая установка запишется следующим образом:
П~ - П~ (а) + П~ (Р).
Рассматриваемая задача примет вид:
Я-АЯ = ЯП-АЯП+(ЯИ-АЯИ), ¦ АЯП а Ш р’
Решив ее, получим:
АПп Д/7И
хД/7и
~Г~
АП
1+"
Проверка, а = 0,3; Р = 0,7; #п = 12; #и = 8; П = 20; АП = 2; АП = 1,399; АП = 0,599; П - АП = 12 - 0^599 = 11,4; П - АП = = 8- 1,399 = 6,6; П -АП= 11,4 + 6,6= 18.
Эта задача содержит аддитивную функцию и одинаковые знаки приростов, поэтому она может быть решена также простым делением прироста функции между аргументами (см. п. 1.3).
Решение задач без указания приоритетности целей
Достаточно часто важность целей установить или невозможно, или затруднительно. Иногда такая характеристика не интересует лицо, формирующее решение.
Например, если у функции 7-10 аргументов, то определить важность целей, отражаемых с их помощью, весьма проблематично. Существуют специально разработанные для этого методы, например, метод анализа иерархий Саати, однако этот и другие методы требуют значительных дополнительных усилий [7]. Очень часто перед лицом, формирующим решение, стоит задача добиться цели без указания каких-либо приоритетов в путях ее достижения.
В таких случаях задача обратных точечных вычислений упрощается и сводится к решению уравнений с одним неизвестным. Им служит единый коэффициент, на который следует либо умножить, либо разделить исходные значения аргументов, чтобы получить желаемый прирост функции.
Как и ранее, функция дополняется целевыми установками, однако КОВ отсутствуют.
Пусть задана функция у = f(x, z). Как и ранее, в соответствии с целевыми установками возникают следующие варианты обратных точечных вычислений:
y±=f(x±9z±).
Как видим, КОВ отсутствуют.
23. Целевая установка: у+ = /(л:+, z+).
Если ввести единый коэффициент к, то можно получить:
х + Ах = кх; z + Az = kz.
Задача обратных вычислений примет вид:
у + Ау = f(kx, kz).
Пример (рис. 2.21).
Воспользуемся задачей из целевой установки 1, где речь шла об исчислении прибыли по формуле П = В-С, а Я прибыль; В - выручка; С - себестоимость продукции.
Допустим, целевая установка состоит в следующем: необходимо повысить прибыль за счет увеличения выручки и себестоимости. Такая целевая установка представляется следующим образом:
П+ =В+-С+.
Представим эту задачу в виде выражения:
П + АП = В + АВ-(С + АС).
Введем величину к и запишем:
В + АВ = кВ,
С + АС = кС.
П + АЛ -кВ-кС - к(В - С),
откуда получим
, П + АП Я
Проверка. В = 20; С = 8; П = 12; АП = 8; к = 1,66; П + ДЯ = = 1,66- 20- 1,66- 8 = 20,05 -20.
24. Целевая установка: = /(л;+, г ).
Задача обратных вычислений имеет вид: у + Ay = /(far, ).
Пример. Обратимся к задаче из целевой установки 2, предназначенной для расчета рентабельности по формуле
где Р - рентабельность;
П - прибыль;
С - себестоимость продукции.
Пусть, как и ранее, целевая установка следующая: увеличить рентабельность за счет повышения прибыли и снижения себестоимости. Такая целевая установка представляется следующим образом:
Р+
П +
С~ ’
Введем коэффициент к и запишем:
П + АП = кП,
С-АС =. к
Подставив эти выражения в общую функцию, получим откуда
Р + ДР
= 9,987 10.
Р+ДР:
Проверка. П = 24; С = 4; Р = 6; АР = 4; к = 1,29; 30,96
3,1
25. Целевая установка: = /(л: , г+).
Обратная задача имеет вид: У + Ду = /(, ?z).
Пример (рис. 2.22). Если формула для прямого расчета
А = В-С,
а целевая установка отражена следующим образом:
А+ =В~-С+,
то наша задача примет вид
А + АА = кС.
к
В ней использованы следующие обозначения:
В-АВ=~,
к
С + АС = кС.
Решив уравнение относительно к, получим:
_ -(А + АА) + уІ(А + АА)2 + 4СВ 2С '
Проверка. В = 80; С = 8; А = 12; = 4; к = 1,04; ^ + АЛ = 34,78 -
- 18,4= 16,38 16.
Если возникает потребность в поиске значений аргументов, обеспечивающих уменьшение функции, то здесь возможности данной модификации ограничены. В таких случаях следует обратиться к иным модификациям метода. Задача обратных вычислений с аддитивной функцией и с обоими отрицательными приростами аргументов может быть решена с помощью данного метода.
Рассмотрим ее.
26. Целевая установка: у = f(x , г ).
Задача обратных вычислений имеет вид:
y-Ay = f(*L).
к к
Пример. Допустим, прямая формула расчета следующая:
А - В-С.
Если целевая установка
А~ = ВТ - С,
то задача обратных вычислений запишется следующим образом:
А-ЬЛ = -к
Решая ее, получим к = .
А-АА
Проверка. А = 12; ЬЛ = 4; В = 20; С = 8; к = 1,5; В - ДВ = 13,33; С - АС = 5,33; А-АА = 13,33 - 5,33 = 8.
Рассмотрим еще один пример с аддитивной функцией, но уже с тремя аргументами.
Допустим, необходимо снизить величину оборотного капитала И за счет снижения производственных запасов 3, снижения
незавершенного производства Н и увеличения денежных средств С. Формула расчета
# = 3 + + С,
которая в соответствии с целевой установкой приобретает вид:
И~ =3~ +Н~ +С+.
Введем искомый коэффициент и получим:
3-АЗ = , Н -АН = , С л-АС = кС,И-АИ = + + кС, к к к к
Ск2 -(И - АИ)к + (3 + Н) = 0.
Решив уравнение, получим
, И -АИ + J(fi-AM)2 -4С(3 + Н) к =-:-1-.
2 С
Проверка (рис. 2.23).
И = 35; АИ = 5; 3 = 10; Я = 20; С = 5; к = 4,73; 3 - АЗ = 2,11; Я - ДЯ = 4,22; С + АС = 23,66; И - ДЯ = = 2,11 + 4,22 + 23,66 = 29,99 * 30.
2.5.
Решение задач с помощью процедуры свертки/развертки
Процедура свертки/развертки применяется для упрощения процесса решения задач обратных точечных вычислений, которые используют прямые функции с числом аргументов больше двух. Процедура свертки/развертки базируется на понятии элементарной базовой конструкции (ЭБК). Эта конструкция содержит в себе только три элемента, которые приведены к стандартному виду и два из которых соединены одной из четырех арифметических операций (+, -, *, Г).
Большинство экономических расчетов можно свести к ЭБК, что позволяет достаточно просто решить ряд задач. В качестве примеров ЭБК можно привести следующие выражения:
Р~ = П+ (а) - С+ (Р); D- = К+ (а) + Т~ (р);
D+ Я
П+ = А+ (а) - В+ (Р); Р =7^Л'
Процедура свертки уже рассмотрена в п. 1.2, поэтому остановимся на процедуре развертки.
Аддитивные функции
27. Целевая установка: Р+ = Я+ (а) + С+ (р) + Т+ (у) + 0+ (X).
Процесс свертки/развертки можно продемонстрировать с помощью рис. 2.24, на котором отражены следующие шаги процедуры свертки/развертки:
Р+ = Я+(а) + Я+(а); Я+= С++Г++0+; а = р + а + А,;
=С+(р) + Я1+(?|/); Я1+=Г+(у) + 0+(^); \|/ = у + А,.
Задачу будем решать с помощью индивидуальных коэффициентов прироста аргументов. Вначале отыскиваются приросты фиктивной вершины D и реальной Я обычным способом:
Я + АЯ = А:1Я, D + ЛЯ = k2D,
; а(Р + АР) + оЯ - а? t (Р + АР)-кхП
1 П 2 D
Для того чтобы определить прирост фиктивной вершины Z)l, необходимо нормализовать веса Р и \|/ следующим образом:
Р' =
Р
Р + ?’
Тогда получим приросты фиктивной вершины D1 и реальной С следующим образом:
С +АС = къС, Dl + ADl = кф\,
, _ р'ф + А?) + ?|/'С-Р'?1 , _ф + М))-къС
3 С 4 Dl
Для того hto6ji рассчитать приросты аргументов Т и Z), предварительно следует нормализовать их веса:
г , /? . - у+Х у+Х
Приросты оставшихся аргументов:
Т + АТ = к5Т, 0 + А0 = к60,
, _ y'(?1 + AD1) + XT-y'C , _ (Dl + ADl)-ksT
*5 т ’ 6 о -
Пример (рис. 2.25). Оборотный капитал предприятия можно рассчитать по формуле
9 = Я+С + 7\
где О - стоимость оборотного капитала в некотором периоде;
Я - стоимость производственных запасов;
С - стоимость незавершенного производства;
Т - стоимость прочих элементов оборотного капитала (готовая продукция, денежные средства и пр.).
Допустим, необходимо повысить общую стоимость оборотного капитала за счет повышения стоимости всех его элементов. Такая целевая установка отразится следующим образом:
0+ = Я+(а) + С+(р) + Г+(у).
Свернем эту формулу:
С+(р) + Г(у) = Я+(а); а = р + Х.
Тогда
0+ =Я+(а) + Я+(ст).

Приросты для аргументов П и D равны:
П + АП = кх П\ D + AD = k2D. Отсюда коэффициенты для расчета приростов:
*.=
а (О + АО) + аП - аD
П
к2 =
(0 + А0)-к}Л D '
Приросты для аргументов Си Травны:
С + АС = кгС,Т + АТ = к4Т,
Р+у р+у Тогда коэффициенты для расчета приростов:
Э'__Ё_, / = . У
, p'(I + AD) + y'C-pT , (D + AD)-k3C
*3 ~ 9 ^4 ~ _ -
Проверка. П = 60; С = 30; Т = 10; О = 100; ДО = 40; а = 0,6; Р = 0,1; у = 0,3; D = 40; Р' = 0,25; І = 0,75; kx = 1,4; k2 = 1,4; П +АП = = 1,4 - 60 = 84; D + AD = 1,4 - 40 = 56; = 1,13; kt = 2,2; С + ДС =
= 1,13 - 30 = 33,9; T+ AT= 2,2 - 10 = 22; О + ДО = 84 + 33,9 + 22 = = 139,9 140.
Мультипликативные функции
28. Целевая установка: Р+ = Я+ (а) - С* (р) - Т* (у) - Ф+ (X).
Как и ранее, вначале эту функцию следует свернуть:
Р+ =n+(a) D+(a); D+ = С+(р)?+(\|/); а = р + у + Х.;
Содержание раздела