Одинцов Б. - Обратные вычисления в формировании эк решений
Обратные вычисления относятся к наиболее капризным и трудным задачам. Объясняется это непредсказуемостью поведения обратной функции, форма записи которой, как правило, либо неизвестна, либо представлена приближенно.
Отсюда возникает проблема определения диапазонов исходных данных, при которых задача имеет решение.
Если прямые зависимости, получаемые в процессе изучения связей между событиями, отражают существующее положение вещей (воспроизводят как есть) и обычно рассматриваются в качестве первичных, то обратные зависимости, полученные из уже имеющихся, с одной стороны, прямых зависимостей, а с другой -обратными функциями, находят, исходя из целей управления, которое отсутствует в прямых зависимостях.
Объективно обратные вычисления должны рассматриваться в качестве вторичных, так как зависят от целей воздействия на те или иные события, и их решение обусловлено прямыми задачами.
В пособии изложен один из методов решения обратных задач, названный автором обратными вычислениями. Специфика такого рода вычислений заключается в том, что они не требуют знания обратной функции. Метод ориентирован на получение отдельных значений аргументов прямой функции на основе задаваемого для нее прироста. Для того чтобы задача была корректной, она доопределяется с помощью дополнительной информации, касающейся целей решения обратной задачи.
Вычисления называются точечными, так как позволяют найти некоторые точки в диапазоне возможных изменений аргументов функции.
Метод обратных вычислений имеет несколько модификаций, которые при решении одной и той же прикладной задачи дают различные результаты. Разница в результатах тем заметнее, чем больший требуется прирост функции. Какую из модификаций применять в каждом конкретном случае, зависит от специфики предметной области.
Здесь необходимы дополнительные исследования, в результате выполнения которых можно было бы дать однозначный ответ на вопрос: Какая модификация метода наиболее целесообразна в данном случае?.
В пособии рассмотрены задачи, которые поделены на три класса: детерминированные, стохастические и решаемые в условиях неопределенности. Для всех трех классов выведены типовые целевые установки, возникающие в процессе управления.
Эти установки позволяют привести любую функцию, используемую для прямого расчета, к виду, который позволяет выполнить обратные вычисления.
Особенно подробно рассмотрены задачи, выраженные детерминированными зависимостями. Здесь удалось разработать достаточно простую процедуру свертки/развертки, которая позволяет сводить громоздкие исходные зависимости к функциям с двумя переменными.
Такие функции обеспечивают использование стандартных операций для их обработки.
Задачи, решение которых предназначено для учета рисков, представлены следующими видами вероятностей:
безусловные вероятности наступления одного из несовместных событий;
безусловные вероятности наступления одного из совместных событий;
условные вероятности наступления всех возможных несовместных событий и т.д.
Здесь можно отметить, что формулы для прямых вероятностных расчетов уже известны. Отсюда обратные вычисления можно свести к набору стандартных процедур.
По мере повышения уровня интеллектуализации различного рода прикладных систем, в том числе и систем формирования решений, приходится все больше отказываться от детерминированных или стохастических зависимостей между событиями и переходить к средствам, способным воспроизводить условия неопределенности.
Детерминированные зависимости, как правило, чрезвычайно идеализируют связи между событиями, а применение стохастических связей ограничивается сложностью получения исходных данных.
Представление связей между событиями с помощью нечетких множеств первого и второго рода вынуждает прибегать к разработке специальных средств, позволяющих выполнять обратные вычисления. Для воздействия на реальные события в условиях неопределенности эти средства должны обеспечить:
сочетание субъективных оценок правил вывода с объективной информацией в базе данных, природа которых различна;
сочетание различных шкал, применяемых для измерения субъективной и объективной информации.
Применение обратных вычислений в условиях неопределенности, несмотря на всю свою перспективность, остается одним из самых малоразработанных направлений создания интеллектуальных систем.
Одна из глав (5-я) демонстрирует возможности некоторых модификаций метода в решении инженерных задач. Здесь для иллюстрации выбрано несколько типовых расчетов: логарифмические, степенные и показательные функции, а также вычисление площадей различных фигур, заданных определенными интегралами, решение дифференциальных уравнений в приложении к различным техническим задачам.
Настоящее издание является учебным, поэтому в нем не ставилась задача строгого доказательства тех или иных математических утверждений. Большинство из них достаточно прозрачны, а их корректность проиллюстрирована на многочисленных примерах.
Тщательное рассмотрение большинства возможных вариантов решения задач базируется на детерминированных зависимостях, что позволило остальные типы задач, а именно стохастические и задачи, решаемые в условиях неопределенности, представить не так полно, ибо появилась возможность делать соответствующие ссылки.
Большинство расчетов в экономике осуществляется на основе простейших арифметических формул, что позволяет сводить их с помощью специальной процедуры к функциям с двумя аргументами. Это упрощает проблему вычислений, так как появляется возможность обращаться к набору базовых, т.е. типовых, функций, для которых уже известны стандартные расчетные формулы.
Каждый конкретный случай формирования решений можно свести к набору типовых процедур, поэтому для удобства выполнения расчетов в конце учебного пособия приведены приложения, в которых находятся типовые целевые установки и используемые при этом стандартные формулы для обратных вычислений. В приложении 1 представлены типовые операции для обработки детерминированных зависимостей, в приложении 2 -для вероятностных зависимостей, в приложении 3 - для приближенных рассуждений, а в приложении 4 - для логарифмических, показательных и степенных функций.
Автор считает своей обязанностью поблагодарить всех, кто прямо или косвенно поддерживал данное направление на протяжении многих лет. Это прежде всего касается Заслуженного деятеля науки РФ, д.э.н., проф. А.Н.
Романова, который систематически стимулировал и направлял работу в данной области, а также д.э.н., проф. В.В.
Дика, приложившего значительные усилия в разработке процедуры свертки/развертки, чьи критические замечания заметно способствовали улучшению качества рукописи.
В проверке результатов и разработке программного обеспечения, поддерживающего процесс решения обратных задач на детерминированных зависимостях, принимали участие студенты и аспиранты, перечислить которых невозможно. Всем им автор приносит свою благодарность.
Глава 1ОСНОВЫ ОБРАТНЫХ ВЫЧИСЛЕНИЙ
1.1.Обратные задачи и обратные вычисления
Фундаментальные особенности человеческого восприятия окружающего мира предопределяет изучение его с помощью парных категорий, среди которых можно выделить следующие:
причина- следствие
При этом категория, находящаяся слева от стрелки, всегда является первичной, так как от нее зависит категория, находящаяся правее. Это позволило К. Попперу в своей книге Открытая Вселенная: аргумент в пользу индетерминизма сформулировать следующее: ...здравый смысл склонен утверждать, что любое явление обусловлено теми или иными предшествующими явлениями и поэтому любое явление может быть объяснено или предсказано... [2].
Если данное утверждение принимается, то это значит, что принимается позиция Аристотеля, которая заключается в том, что главное предназначение науки состоит в изучении и объяснении причин, повлекших за собой те или иные события (последствия) в природе и обществе.
Результаты изучения подчиненности вторичных категорий первичным находят свое отражение с различной степенью адекватности в прямых зависимостях (следствий от причин, результатов от затрат, достижения целей от средств и т.д.). Эти зависимости воспроизводят существующее положение вещей, т.е. воссоздают то, как есть.
В обобщенном виде результаты изучения прямых связей можно представить следующим образом:
следствие = /(причина), результат = /(затраты), достижение цели = ^средства),
где / указывает на прямую связь между причиной и следствием, средствами и целью, затратами и результатами и т.д.
Внимательно вглядываясь в попперовско-аристотелевские разъяснения предназначения науки, мы, однако, не находим того, что объективно сопровождает всякую осмысленную деятельность человека и в том числе ученого, - это цель его деятельности. Между тем изучение и объяснение этих самых причин происходит с вполне определенной целью, преследуемой ученым.
Человек в силу своей природы после изучения того, как есть непременно инициирует процесс перехода к тому как нужно. Человеку не свойственна лишь пассивная констатация фактов или событий, ему в подавляющих случаях требуется подчинить себе эти события, повлиять на них в соответствии со своими потребностями.
Такого разъяснения мы не находим в цитированном труде.
Процесс перехода к тому, как нужно, т.е. влияние на события, требует дополнения в зависимости между событиями информации, отражающей антропоморфные цели. Кроме того, сами зависимости должны рассматриваться задом наперед.
Если ранее в качестве ведущих понятий рассматривались причина, средства, затраты, а в качестве ведомых - следствие, цель, результаты, то теперь они должны поменяться местами. В обобщенном виде такую трансформацию можно представить следующим образом:
причина = ^(следствие), затраты = ^(результаты), средства = #(цель),
где g указывает на обратную зависимость между используемыми понятиями.
Здесь мы приходим к обратной задаче, ибо цель исследования событий как таковых принципиально отличается от цели исследования, результаты которого предназначены для последующего влияния на эти события человеком. Первичным является изучение и воспроизведение прямых связей, т.е. того, как есть, вторичным - изучение обратных связей с целью изменения того, как есть на то, как должно быть.
При этом существует довольно важная особенность: изучение обратных связей возможно лишь при наличии результатов изучения прямых связей.
Существует фундаментальное различие между прямыми зависимостями (обозначенными ранее как f) и зависимостями, которые получают с целью последующего влияния на эти события (обозначенными как g). Если первые воспроизводят существующие связи между событиями, то вторые предназначены для нарушения, т.е. изменения этих связей в соответствии с внешними по отношению к ним целями. Получение обратных зависимостей и есть'результат постановки и решения обратных задач.
Вполне естественно, что главное внимание должно уделяться прямым зависимостям, ибо они цель и результат всякой науки. Вторичные (обратные) связи, не упоминающиеся в попперовско-аристо-телевских воззрениях, находятся как бы в тени (в положении золушки, ждущей своего часа).
Их звездный час приходит лишь в том случае, если возникла потребность во вмешательстве в существующий ход событий, в его изменении в соответствии с целями управления.
Может возникнуть путаница в используемой терминологии. Поэтому обратимся к классическому изображению системы управления, представленной на рис.
1.1. Обычно в таких схемах используются термины прямая и обратная связь: прямая связь несет в себе директивную информацию, а обратная - отчет об исполнении предписаний. Чтобы избежать путаницы, будем употреблять эти термины, если в процессе управления обратные задачи на решаются. Тогда контур управления на этом рисунке представляется пунктирными линиями.
Если же обратные задачи ставятся и решаются, то контур управления сохраняется, однако используемые при этом средства будут иными. На рассматриваемом рисунке он отражается с помощью сплошных линий.
Статус обратных зависимостей, рассматриваемых с позиции главного предназначения науки как чего-то второстепенного, не мог не повлиять на уровень развития многих прикладных систем
|
||||||||||||||||||||||||||||||||||||||||||||||
| Рис. 1.1 |
Главная причина такого достаточно плачевного положения дел состоит в том, что эти системы изначально не в состоянии выдавать информацию, необходимую для воздействия на вполне реальные события, ибо в них не заложены основы такого воздействия - обратные зависимости. Наличие прямых зависимостей (детерминированных или стохастических) мало чем может помочь, ибо они воспроизводят то, что есть. Верх возможностей такого рода систем - это констатация фактов, их анализ и ответ на вопрос: Что будет, если?. В результате системы не могли ответить на вопрос: Как сделать, чтобы?. Отсюда резкое угасание интереса к подобного рода системам, пессимизм, разброд и шатание. Для того чтобы системы стали полезными, т.е. с их помощью можно было реально влиять на события, в основу их построения, кроме формализованных прямых зависимостей, должны быть положены и обратные, рассматриваемые сквозь призму антропоморфных целевых установок.
Для этого они должны уметь решать обратные задачи. Приведем примеры прямых и обратных к ним задач экономического профиля.
Системы, ориентированные па формирование решений в условиях определенности (детерминированные зависимости)
1. Пр я м а я задача: Какова рентабельность предприятия?
Обратная задача: Что следует предпринять, чтобы рентабельность повысилась на А %?
2. П р я м а я задача: Какова конкурентоспособность предприятия?
Обратная задача: Что следует предпринять, чтобы конкурентоспособность повысилась на В единиц?
3. Пр я м а я задача: Какова выручка предприятия за месяц?
Обратная задача: Что следует предпринять, чтобы выручка увеличилась на К единиц?
Системы, ориентированные на формирование решений в условиях неопределеннсти
1. Пр я м а я задача: Каково доверие к заключению Акции данного предприятия поднимутся в цене.
Обратная задача: Что следует предпринять, чтобы акции данного предприятия поднялись в цене на А единиц?
2. Прямая задача: Каково доверие к заключению ВВП в будущем периоде увеличиться на К единиц.
Обратная задача: Что следует предпринять, чтобы ВВП в будущем периоде увеличился на К единиц?
3. Пр я м а я задача: Каково доверие к заключению, что цены на энергоносители в будущем периоде снизятся?
Обратная задача: Что следует предпринять, чтобы цены на энергоносители в будущем периоде не снизились?
Системы, ориентированные на формирование решений в условиях риска (стохастические зависимости)
1. Пр я м а я задача: Какова вероятность наступления одного из независимых событий?
Обратная задача: Что следует предпринять, чтобы данная вероятность повысилась?
2. Пр я м а я задача: Определить вероятность того, что взятая наугад продукция окажется отличного качества.
Обратная задача: Что следует предпринять, чтобы взятая наугад продукция оказалась отличного качества.
Обратные связи воспроизводятся с помощью обратных функций, а задачи, решаемые с их помощью, получили название обратных. Основы систематических исследований обратных задач заложил академик А.Н. Тихонов в своей работе [1], опубликованной в 1943 г. Однако под обратными задачами он понимал изучение свойств объектов, недоступных или неудобных для непосредственного изучения. Поэтому подвергаются изучению те характеристики объекта, которые можно измерить, а затем на их основании отыскать закономерности в развитии самих объектов. А.Н. Тихоновым также введено следующее определение, имеющее теоретическую значимость: пусть некоторая совокупность элементов {х} отображается функцией f(x) на другую совокупность элементов {х*}: х* = f(x). Такое отображение называется
взаимно однозначным в точке xQ9 если Xq =f(xQ)* f(x) для любого элемента х, отличного от х0.
Это определение позволяет доказать следующую теорему: пусть некоторое метрическое пространство R непрерывно отображается на другое метрическое пространство Л*, т.е. х* = /(*), * *
[х е R, х е R ]. Если это отображение взаимно однозначно в точке х0 и пространство R компактно, то отображение х = /~‘0*) также непрерывно в точке х*.
В отличие от содержания обратных задач, исследуемых в работе [1], в нашем понимании такая задача характеризуется прежде всего целью управления, выраженной с помощью значения какого-либо экономического или другого показателя, и наличием прямой функции. Эта функция отражает зависимость следствия от причины, результатов - от затрат, уровня достижения цели -от затраченных для этого средств и т.д.
Обратные задачи характеризуются капризностью и трудоемкостью. Капризность заключается в непредсказуемости поведения функции, вид которой, как правило, либо неизвестен, либо известен приблизительно. Отсюда всегда существует проблема с определением диапазонов значений исходных данных, при которых задача, во-первых, имеет смысл, а во-вторых - имеет решение.
Так как обратную функцию получить трудно, а зачастую и невозможно, существует потребность в разработке метода, который позволил бы решать некоторые обратные задачи без нее. Решения для такого класса задач могут быть частичными, т.е. точечными, базирующимися не на области решений, а на некоторой ее точке.
Метод обратных точечных вычислений, представленный далее, требует немногого: корректно оформленных прямых зависимостей и дополнительной информации о целях, преследуемых лицом, формирующим решение. Дополнительная информация отражается в специально разработанной форме, названной целевая установка. Эта форма позволяет достаточно просто трансформировать исходные формулы в соответствующие постановки обратных задач.
Решение обратных задач с помощью обратных вычислений -это получение точечных значений приростов аргументов прямой функции на основании ее задаваемого значения и дополнительной информации, поступающей от лица, формирующего решение. Точечными они называются потому, что отыскиваются новые значения аргументов лишь для одной заданной точки функции.
Дополнительная информация, используемая при этом, касается:
целевой установки лица, формирующего решение, выражаемой с помощью знаков (увеличение или уменьшение) приростов каждого из аргументов прямой функции;
приоритетности в путях достижения целей, отражаемой с помощью коэффициентов их относительной важности (КОВ).
Полученное решение задачи требует тщательного анализа, ибо вычисленные точечные значения неизвестной обратной зависимости могут быть бессмысленными. Анализироваться должны исходные данные, диапазон их значений, при которых задачи имеют решение. Семантический анализ исходных данных и полученных результатов - одна из обязательных процедур решения обратных задач.
Далее будут использоваться следующие рабочие термины:
прямая зависимость - выражение, отражающее связи между событиями (объектами), которые характеризуют состояние как есть;
прямые вычисления (расчеты), осуществляемые с помощью прямых функций;
обратная зависимость - выражение, отражающее цели, преследуемые лицом, формирующим решение;
обратные точечные вычисления, осуществляемые на основе обратных зависимостей, в результате которых получают искомые приросты аргументов прямой функции.
Применение обратных вычислений в экономике
Рассмотрим, каким образом можно использовать обратные вычисления для формирования управленческих решений, на примере повышения рентабельности предприятия. Подробно этот пример будет демонстрироваться в разд.
2.7, здесь же исследуем принципиальные возможности данного метода.
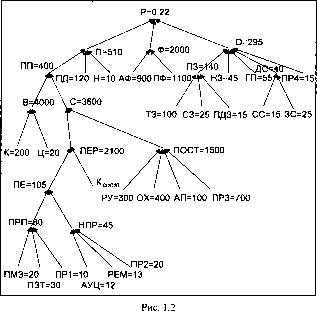
Рассмотрим дерево показателей, предназначенное для расчета рентабельности предприятия. Дерево имеет восемь уровней (рис.
1.2), что вполне достаточно для формирования предписаний различным службам предприятия, выполнение которых должно привести к повышению рентабельности. Стрелки указывают направление расчетов.
На рис. 1.2 не все терминальные (висячие) вершины достаточно детализированы. Например, активная часть основных фондов, от которой во многом зависит эффективность производства, представлена лишь одним показателем.
Для реального принятия решений эти показатели должны детализироваться по структурным подразделениям, по классам основных фондов и т.д. То же касается и оборотного капитала, особенно показателей, характеризующих его отдельные элементы (технологический запас, производственный запас, страховой запас и т.д.).
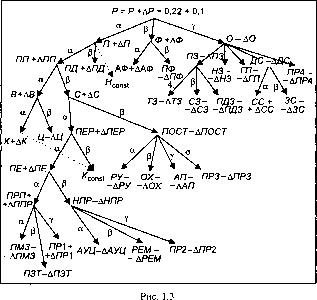
Целевые установки, указанные лицом, формирующим решение, приведены на рис. 1.3.
Коэффициенты относительной важности представлены в табл. 2.1.
Приведем расчетные формулы:
где Р - рентабельность;
П - чистая прибыль, полученная за анализируемый период;
Ф - среднегодовая стоимость основных производственных фондов; О - месячная стоимость оборотных средств.
2. П- ПП + ПД - Я,
где ПП - прибыль от продаж;
ПД - прочие доходы, в том числе чрезвычайные;
Н - налог на прибыль.
з.пп = в-с,
где В - выручка от продажи товаров, продукции, работ, услуг за месяц; С - себестоимость товаров, продукции, работ, услуг за месяц.
4. В = К - Ц,
где К - объем выпуска продукции, шт.;
Ц - цена единицы продукции, руб.
5. С = ПЕР + ПОСТ,
где ПЕР - совокупные переменные расходы; ПОСТ - постоянные затраты.
6 .ПЕР = КПЕ,
где К - объем выпуска продукции, шт.;
ПЕ - переменные затраты, приходящиеся на единицу продукции.
7. ПЕ = ПРП + НПР,
где ПРП - производственные переменные затраты;
НПР - непроизводственные переменные затраты.
Ъ. ПРП = ПМЗ + ПЗТ + ПР\,
где ПМЗ - прямые материальные затраты;
ПЗТ - прямые затраты на оплату труда;
ПР1 - прочие производственные переменные затраты.
9. НПР = А УЦ + РЕМ + ПР2,
где А УЦ - содержание аппарата управления цехом;
РЕМ - содержание и ремонт производственного оборудования;
ПР2 - прочие непроизводственные переменные затраты.
10. ПОСТ= РУ + ОХ + АП + ПРЗ,
где РУ - затраты на оплату труда работников управления;
ОХ - затраты на охрану;
АП - затраты на аренду производственного инвентаря и производственных площадей;
ПРЗ - прочие постоянные затраты.
П.Ф = АФ + ПФ,
где АФ - активная часть основных производственных фондов;
ПФ - пассивная часть основных производственных фондов.
12. 0 = ПЗ + НЗ + ГП+ДС + ПРА,
где ПЗ - производственные запасы;
НЗ . - незавершенное производство;
/77 - готовая продукция;
ДС - денежные средства;
ПРА - прочие элементы оборотного капитала.
Из перечисленных в формуле для О элементов будут вычисляться лишь два, а именно:
13. ПЗ = 73 + СЗ + ЛДЗ,
где ТЗ - текущий запас;
СЗ - страховой запас;
ПДЗ - подготовительный запас.
14. ДС = СС + ЗС9
где СС - собственные денежные средства;
ЗС - заемные денежные средства.
Так как существует проблема повышения рентабельности, возникает обратная задача, которая формулируется следующим образом: на основании
прямых зависимостей показателей;
информации о желаемых направлениях в изменениях показателей;
информации о приоритетности в изменениях показателей;
информации о желаемом приросте рентабельности рассчитать приросты терминальных вершин дерева целей.
Граф показателей превращается в дерево целей с обратным направлением расчетов.
