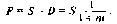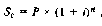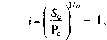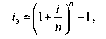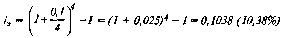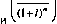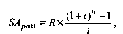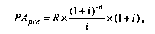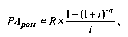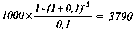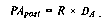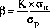Глава 4. Методический инструментарий управления

ПРИБЫЛЬЮ

4.1. КОНЦЕПЦИЯМ МЕТОДИЧЕСКИЙ ИНСТРУМЕНТЛРИЙОЦЕНКИ

СТОИМОСТИДЕНЕГ ВО ВРЕМЕНИ

Управление прибылью требует постоянного осуществления различного рода финансово-экономических расчетов, связанных с потоками денежных средств в разные периоды времени. Ключевую роль в этих расчетах играет оценка стоимости денег во времени.

Концепция стоимости денег во времени состоит в том, что стоимость денег с течением времени изменяется с учетом нормы прибыли на финансовом рынке, в качестве которой обычно выступает норма ссудного процента (или процента).

Иными словами, в соответствии с этой концепцией одна и та же сумма денег в разные периоды времени имеет разную стоимость; эта стоимость в настоящее время всегда выше, чем в любом будущем периоде.

Концепция стоимости денег во времени играет основополагающую роль в практике вычислений, связанных с управлением прибылью. Она предопределяет необходимость учета фактора времени в процессе осуществления любых долгосрочных финансовых и инвестиционных операций путем оценки и сравнения стоимости денег при начале финансирования со стоимостью денег при их возврате в виде будущей прибыли, амортизационных отчислений, основной суммы долга и т.д.

Оценка стоимости денег с учетом фактора времени требует предварительного рассмотрения связанных с ней базовых понятий. Ниже изложено содержание основных из этих понятий.

ПРОЦЕНТ — сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный процент, кредитный процент, процент по облигациям, процент по векселям и т.п.).

ПРОСТОИ ПРОЦЕНТ — сумма дохода, начисляемого к основной сумме капитала в каждом интервале,

И А Бланк

по которой дальнейшие расчеты платежей не осуществляются. Начисление простого процента применяется, как правило, при краткосрочных финансовых операциях.

СЛОЖНЫЙ ПРОЦЕНТ — сумма дохода, начисляемого в каждом интервале, которая не выплачивается, а присоединяется к основной сумме капитала и в последующем платежном периоде сама приносит доход. Начисление сложного процента применяется, как правило, при долгосрочных финансовых и инвестиционных операциях.

ПРОЦЕНТНАЯ СТАВКА (ставка процента) - удельный показатель, в соответствии с которым в установленные сроки выплачивается сумма процента в расчете на единицу капитала. Обычно процентная ставка характеризует соотношение годовой суммы процента и суммы предоставленного (заимствованного) капитала (выраженное в десятичной дроби или в процентах)

БУДУЩАЯ СТОИМОСТЬ ДЕНЕГ - сумма инвестированных в настоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента (процентной ставки).

НАСТОЯЩАЯ СТОИМОСТЬ ДЕНЕГ - сумма будущих денежных средств, приведенных с учетом определенной ставки процента (процентной ставки) к настоящему периоду времени.

НАРАЩЕНИЕ СТОИМОСТИ (компаундинг) - процесс приведения настоящей стоимости денег к их будущей стоимости в определенном периоде путем присоединения к их первоначальной сумме начисленной суммы процентов.

ДИСКОНТИРОВАНИЕ СТОИМОСТИ - процесс приведения будущей стоимости денег к их настоящей стоимости путем изъятия из их будущей суммы соответствующей суммы процентов (называемой "дисконтом ”).

ПЕРИОД НАЧИСЛЕНИЯ — общий период времени, в

г течение которого осуществляется процесс наращения

или дисконтирования стоимости денежных средств.

Раздел I. Концептуальные основы управления прибылью предприятия

ИНТЕРВАЛ НАЧИСЛЕНИЯ — обусловленный конкретный временной срок (в пределах общего периода начисления), в рамках которого рассчитывается отдельная сумма процента по установленной его ставке (осуществляется отдельный платеж процента).

ПРЕДВАРИТЕЛЬНЫЙ МЕТОД НАЧИСЛЕНИЯ ПРОЦЕНТА (метод пренумерандо или антисипативный метод) — способ расчета платежей, при котором начисление процента осуществляется в начале каждого интервала.

ПОСЛЕДУЮЩИЙ МЕТОД НАЧИСЛЕНИЯ ПРОЦЕНТА

(метод постнумерандо или декурсивный метод) — способ расчета платежей, при котором начисление процента осуществляется в конце каждого интервала.

ДИСКРЕТНЫЙ ДЕНЕЖНЫЙ ПОТОК - поток денежных средств по финансовой и инвестиционной деятельности, имеющий четко ограниченный период начисления процентов и конечный срок возврата основной суммы капитала.

НЕПРЕРЫВНЫЙ ДЕНЕЖНЫЙ ПОТОК — поток денежных средств по финансовой и инвестиционной деятельности, период начисления процентов по которому не ограничен, а соответственно не определен и конечный срок возврата основной суммы капитала.

АННУИТЕТ (ФИНАНСОВАЯ РЕНТА) - длительный поток платежей,

характеризующийся одинаковым уровнем процентных ставок на протяжении всего периода.

Среди изложенных базовых понятий, связанных с оценкой стоимости денег во времени, наиболее сложным является понятие процентной ставки, по которой осуществляется процесс наращения и дисконтирования стоимости денежных средств. Это понятие отличается многообразием конкретных его видов, используемых в практике вычислений. Процентная ставка, используемая в процессе наращения или дисконтирования стоимости денежных средств (оценки их будущей и настоящей стоимости), классифицируется по следующим основным признакам (рис. 4.1.).



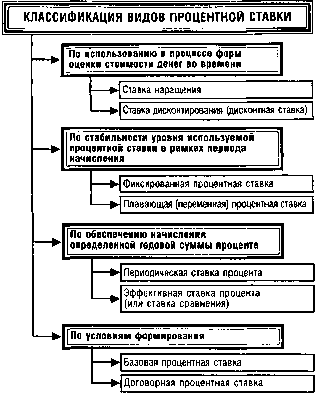
Рнсунок4.1. Классификация видов процентной ставки, используемой в процессе оценки стоимости денег во времени.

1. По использованию в процессе форм оценки стоимости денег во времени различают ставку наращения и ставку дисконтирования (дисконтную ставку).

Ставка наращения представляет собой процентную ставку, по которой осуществляется процесс наращения

стоимости денежных средств (компаундинг), т.е. определяется их будущая стоимость.

Ставка дисконтирования (дисконтная ставка) представляет собой процентную ставку, по которой осуществляется процесс дисконтирования стоимости денежных средств, т.е. определяется их настоящая стоимость.

2. По стабильности уровня используемой процентнойставки в рамках периода начисления выделяют фиксированную и плавающую процентные ставки.

Фиксированная ставка характеризуется неизменным ее уровнем на протяжении всех интервалов общего периода начисления.

Плавающая (или переменная) процентная ставка характеризуется регулярно пересматриваемым ее уровнем по соглашению сторон в разрезе отдельных интервалов общего периода начислений. Такой пересмотр обусловливается изменением средней нормы процента на финансовом рынке (или в отдельных его сегментах), изменением темпа инфляции и другими условиями.

3. По обеспечению начисления определенной годовойсуммы процента различают периодическую и эффективную процентные ставки.

Периодическая ставка процента при обеспечении определенной годовой суммы процента может варьировать как по уровню, так и по продолжительности отдельных интервалов на протяжении годового периода платежей.

Эффективная ставка процента (или ставка сравнения) характеризует среднегодовой ее уровень, определяемый отношением годовой суммы процента, начисленного по периодическим его ставкам, к основной сумме капитала.

4. По условиям формирования различают базовую идоговорную процентные ставки.

Базовая процентная ставка характеризуется определенным исходным ее уровнем в качестве первоначальной основы последующей ее конкретизации кредитором (заемщиком) в зависимости от условий осуществления соответствующей хозяйственной операции.

Договорная процентная ставка характеризует конкретизированный ее уровень, согласованный кредитором

и заемщиком и отраженный в соответствующем инвестиционном договоре.

Система основных базовых понятий позволяет последовательно рассмотреть методический инструментарий оценки стоимости денег во времени в разрезе наиболее характерных вариантов осуществления такой оценки. Этот методический инструментарий дифференцируется в разрезе следующих видов вычислений (рис. 4.2.).

I. Методический инструментарий оценки стоимости денег по простым процентам использует наиболее упрощенную систему расчетных алгоритмов.

1. При расчете суммы простого процента в процессе наращения стоимости (компаундинга) используется следующая формула:

/ = р X п X / ,

где /— сумма процента за обусловленный период времени в целом; Р — первоначальная сумма (стоимость) денежных

средств; п — количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени; / — используемая процентная ставка, выраженная

десятичной дробью. В этом случае будущая стоимость вклада (S) с учетом начисленной суммы процента определяется по формуле:

S = Р + I = Р х (1 + т) .

Пример: Необходимо определить сумму простого процента за год при следующих условиях: первоначальная сумма вклада — 1000 уел. ден. ед.; процентная ставка, выплачиваемая ежеквартально - 20%.

Подставляя эти значения в формулу, получим сумму процента:

I = 1000 х 4 х 0,2 = 800уел. ден. ед.;

будущая стоимость вклада в этом случае составит:

S = 1000 + 800 = 1800 уел. ден. ед.

Множитель (1 + и/) называется множителем (или коэффициентом) наращения суммы простых процентов. Его значение всегда должно быть больше единицы.

В процессе наращения стоимости -> В процессе наращения стоимости В процессе дисконтирова- В процессе дисконтирова- ния стоимости ния стоимости

Рисунок 4.2. Систематизация основных методических подходов к оценке

В процессе наращения стоимости

В процессе дисконтирования стоимости

стоимости денег во времени.

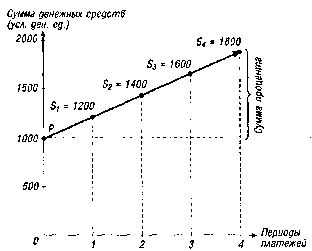
Процесс наращения суммы вклада во времени по простым процентам может быть представлен графически (рис. 4.3.).

Рисунок 4.3. График наращения суммы денежных средств по простым процентам (при процентной ставке 20%). 2. При расчете суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта) используется следующая формула:

D=S-Sx

где D

1 + ш '

сумма дисконта (рассчитанная по простым процентам) за обусловленный период времени в целом;

S — стоимость денежных средств;

и —количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени;

/ — используемая дисконтная ставка, выраженная десятичной дробью.

В этом случае настоящая стоимость денежных средств (Р) с учетом рассчитанной суммы дисконта определяется по следующим формулам:

Пример: Необходимо определить сумму дисконта по простому проценту за год при следующих условиях: конечная сумма вклада определена в размере 1000 уел. ден. ед.; дисконтная ставка составляет 20% в квартал.

Подставляя эти значения в формулу расчета суммы дисконта, получим:

D = 1000 - 1000

---= 444

1 + 4x0,2 у_Сл. $_ен. _е$.

Соответственно настоящая стоимость вклада, необходимого для получения через год 1000 уел. ден. единиц, должна составить:

Р = 1000 - 444 = 556 уел. ден. ед.

-• Используемый в обеих случаях множитель f 1 называется дисконтным множителем (коэффициентом; суммы простых процентов, значение которого всегда должно быть меньше единицы.

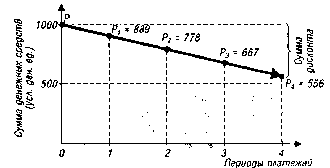
Процесс дисконтирования суммы денежных средств может быть представлен графически (рис. 4.4).

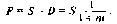
Рисунок 4.4. График дисконтирования суммы денежных средств по простым процентам (при дисконтной ставке 20%). П. Методический инструментарий оценки стоимости денег во сложным процентам использует более обширную и более усложненную систему расчетных алгоритмов. 1. При расчете будущей суммы вклада (стоимости денежных средств) в процессе его наращения по сложным процентам используется следующая формула:

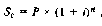
где S_c — будущая стоимость вклада (денежных средств) при его наращении по сложным процентам;

Р — первоначальная сумма вклада;

i — используемая процентная ставка, выраженная десятичной дробью; n —количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Соответственно сумма процента (1_С) в этом случае определяется по формуле:

С — S_c ~ Р ,

Пример: Необходимо определить будущую стоимость вклада и сумму сложного процента за весь период инвестирования при следующих условиях: первоначальная стоимость вклада — 1000 уел. ден. ед.; процентная ставка, используемая при расчете суммы сложного процента, установлена в размере 20% в квартал; общий период инвестирования — один год. Подставляя эти показатели в вышеприведенные формулы, получим:

Будущая стоимость вклада =

= 1000 х (1 + 0,2)⁴ = 2074 уел. ден. ед.

- Сумма процента =

= 2074 - 1000 = 1074 уел. ден. ед.

D_r=S - Р

Пример: необходимо определить настоящую стоимость денежных средств и сумму дисконта по сложным процентам за год при следующих условиях: будущая стоимость денежных средств определена в размере 1000 уел. ден. ед.;

используемая для дисконтирования ставка сложного процента составляет 20% в квартал.

Подставляя эти значения в формулы, получим: Настоящая стоимость — уел. ден. ед.

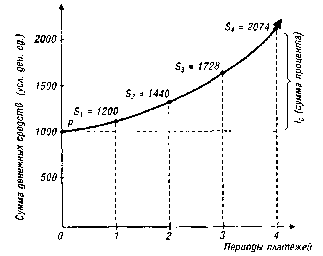
Графически процесс наращения стоимости вклада по сложным процентам представлен на рис. 4.5.

Рисунок 4.5. График наращения суммы денежных средств по сложным процентам (при процентной ставке 20%). 2. При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам используется следующая формула: S (1 + if ’ где Рс—первоначальная сумма вклада; S — будущая стоимость вклада при его наращении; / — используемая дисконтная ставка, выраженная десятичной дробью; л—количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени. Соответственно сумма дисконта (Dc) в этом случае определяется по формуле:

^рс=

1000

(1 + 0,2)4

- 482

Сумма дисконта = 1000 - 482 = 518 уел. ден. ед.

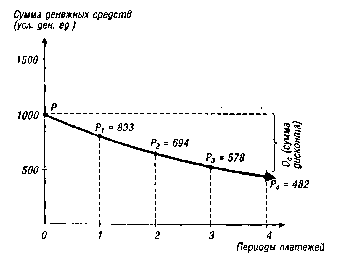
Графически процесс дисконтирования денежных средств по сложным процентам представлен на рисунке 4.6.



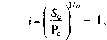
применяется

сложным процентам,

стоимости денежных средств по следующая формула:

где /— средняя процентная ставка, используемая в расчетах стоимости денежных средств по сложным процентам, выраженная десятичной дробью; S_c — будущая стоимость денежных средств; Рс — настоящая стоимость денежных средств; и — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Пример: необходимо определить годовую ставку доходности облигации при следующих условиях: номинал облигации, подлежащий погашению через три года, составляет 1000 уел. ден. ед.; цена, по которой облигацияреализуется в момент ее эмиссии, составляет 600 уел. ден. ед.

Подставляя эти значения в формулу, получим: годовая ставка доходности =

- -1 -1,666?³ - 1 = 0,186 (18,6%).

[б00 ) ' ⁷

4. Длительность общего периода платежей, выраженная количеством его интервалов, в расчетах стоимости денежных средств по сложным процентам определяется

_;i=\og(SJ?_Q) ^

путем логарифмирования log (1 +1) _п0 следующей формуле:

где S_c — будущая стоимость денежных средств; Рс — настоящая стоимость денежных средств; /— используемая процентная ставка, выраженная десятичной дробью.

5. Определение эффективной процентной ставки в процессе наращения стоимости денежных средств по сложным процентам осуществляется по формуле:

Рисунок 4.6. График дисконтирования суммы денежных средств по сложным процентам (при дисконтной ставке 20%). 3. При определении средней процентной ставки, используемой в расчетах

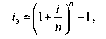
где |_э — эффективная среднегодовая процентная ставка при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

i — периодическая процентная ставка, используемая при наращении стоимости денежных , средств по сложным процентам, выраженная о десятичной дробью;

яи— количество интервалов, по которым осуществляется каждый процентный платеж по периодической процентной ставке на протяжении года.

Пример: необходимо определить эффективную среднегодовую процентную ставку при следующих условиях:

денежная сумма 1000 уел. ден. ед. помещена в коммерческий банк на депозит сроком на 2 года; i годовая процентная ставка, по которой ежеквартально осуществляется начисление процента, со ставляет 10% (0,1).

Подставляя эти значения в формулу, получим:



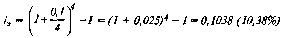
Результаты расчетов показывают, что условия помещения денежной суммы сроком на 2 года под 10% годовых при ежеквартальном начислении процентов, равнозначны условиям начисления этих процентов один раз в год под 10,38% годовых (10,38% составляет размер эффективной или сравнимой процентной ставки).

При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает большое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.

Пример: Перед инвестором стоит задача разместить 100 уел. ден. ед. на депозитный вклад сроком

на один год. Один банк предлагает инвестору выплачивать доход по сложным процентам в размере 23% в квартал; второй — в размере 30% один раз в четыре месяца; третий — в размере 45% двараза в году; четвертый — в размере 100% одинраз в году.

Для того, чтобы определить, какой вариант инвестирования лучше, построим следующую таблицу:

условиях инвестирования (уел. ден. ед.)

Таблица 4.1. Расчет будущем стоимости вклада при различных

^ ! Настоящ ая стоимос Ставка процента Будущая стоимость вклада в конце 1-го период 2-го период 3-го период 4-го период 1 2 100 100 23 123 151 186 229 3 4 100 100 30 130 169 220 45 145 210 100 200

Сравнение вариантов показывает, что наиболее эффективным является 1-й вариант (выплата дохода вразмере 23% один раз в квартал).

Используемые в процессе оценки стоимости денег множители (1 + i)ⁿ

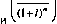
] называются соответствен

но множителем наращения и множителем дисконтирования суммы сложных процентов. Они положены в основу специальных таблиц инвестиционных вычислений, с помощью которых при заданных размерах ставки процента и количества платежных интервалов можно легко вычислить настоящую или будущую стоимость денежных средств по сложным процентам (см. приложения 1 и 2).

III. Методический инструментарий оценки стоимости денег при аннуитете связан с использованием наиболее сложных алгоритмов и определением метода начисления процента — предварительным (пренумерандо) или последующим (постнумерандо).

1. При расчете будущей стоимости аннуитета наусловиях предварительных платежей (пренумерандо) используется следующая формула:

где SA_pre — будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо); Л —член аннуитета, характеризующий размер отдельного платежа; / — используемая процентная ставка, выраженная десятичной дробью; и —количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условияхпредварительных платежей (пренумерандо), при следующих данных:* период

платежей по аннуитету предусмотрен в количестве 5 лет;

интервал платежей по аннуитету составляет один год (платежи вносятся в начале года); сумма каждого отдельного платежа (члена аннуитета) составляет 1000 уел. ден. ед.; используемая для наращения стоимости процентная ставка составляет 10% в год (0,1). Подставляя эти значения в приведенную формулу, получим:

будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), рав-

, на: 1000х⁽¹-+-°¹)~¹ х (1 + 0,1) = 671бусл. ден. единиц.

2. При расчете будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнуме-рандо), применяется следующая формула:



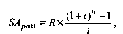
где SAp_0st — будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо); R— член аннуитета, характеризующий размер

отдельного платежа; i — используемая процентная ставка, выраженная десятичной дробью; п — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), по данным, изложенным в предыдущем примере (приусловии взноса платежей в конце года).

Подставляя эти данные в приведенную формулу, получим:

будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо),

равна.усл. ден. единиц.

тох

= 6105

Сопоставление результатов расчета по двум примерам

показывает, что будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей, существенно превышает будущую стоимость аннуитета, осуществляемого на условиях последующих платежей, т.е. в первом случае плательщику обеспечена гораздо большая сумма дохода.

3. При расчете настоящей стоимости аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), используется следующая формула:



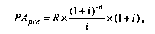
где РА_рге — настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо); R — член аннуитета, характеризующий размер отдельного платежа;

147

/ — используемая процентная (дисконтная) ставка,

выраженная десятичной дробью; « — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени. Пример: Необходимо рассчитать настоящую стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), при следующих данных:

период платежей по аннуитету предусмотрен в количестве 5 лет;

интервал платежей по аннуитету составляет один год (при внесении платежей в начале года); сумма каждого отдельного платежа (члена аннуитета) составляет 1000 уел. ден. ед.; используемая для дисконтирования стоимости ставка процента (дисконтная ставка) составляет 10% в год (0,1).

Подставляя эти значения в приведенную формулу, получим:

настоящая стоимость аннуитета, осуществляемого на условиях предварительных

mOxldLх (2+0,1)- 4169

платежей (пренумерандо), равна.усл. ден. единиц.

4. При расчете настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (пост-нумерандо), применяется следующая формула:



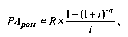
где PA_post — настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо); R — член аннуитета, характеризующий размер отдельного платежа; / — используемая процентная (дисконтная) ставка, выраженная десятичной дробью; и —количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), по данным, изложенным в предыдущем примере (приусловии взноса платежей в конце года).

Подставляя эти данные в приведенную формулу, получим:

настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо),



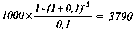
равна:

уел. ден. единиц.

Сопоставление результатов расчета по двум последним примерам показывает, что настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей, существенно превышает настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей, т.е. в первом случае в процессе дисконтирования инвестору гарантирована гораздо большая сумма дохода в настоящей стоимости.

5. При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется следующая формула:

R — SAp_0Slx-

0 + 0"-1

аннуитету (член аннуитета при

где R — размер отдельного платежа по предопределенной будущей его стоимости); SAp_0St — будущая стоимость аннуитета (осуществляемого на условиях последующих платежей); i — используемая процентная ставка, выраженная десятичной дробью; я — количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.

6. При расчете размера отдельного платежа при заданной текущей стоимости

_R-_PA

аннуитета используется такая формула: ¹ ^^{1 +}

где R — размер отдельного платежа по аннуитету (член аннуитета при известной текущей его стоимости); PApost— настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей); /— используемая процентная ставка, выраженная десятичной дробью; и— количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени. В процессе расчета аннуитета возможно использование упрощенных формул, основу которых составляет только член аннуитета (размер отдельного платежа) и соответствующий стандартный множитель (коэффициент) его наращения или дисконтирования.

В этом случае формула для определения будущей стоимости аннуитета

(осуществляемого на условиях последующих платежей), ^^post ^ ^ ’ имеет вид:

где SA_post — будущая стоимость аннуитета (осуществляемого на условиях последующих платежей); R — член аннуитета, характеризующий размер

отдельного платежа; ІА — множитель наращения стоимости аннуитета, определяемый по специальным таблицам, с учетом принятой процентной ставки и количества интервалов в периоде платежей.

Соответственно, формула для определения настоящей стоимости аннуитета имеет

вид:



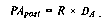
где PAp₀s_t — настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей); R — член аннуитета, характеризующий размер отдельного платежа; Da —дисконтный множитель аннуитета, определяемый по специальным таблицам, с учетом принятой процентной (дисконтной) ставки и количества интервалов в периоде платежей.

В приложениях 3 и 4 приведены множители наращения стоимости аннуитета и его дисконтные множители.

Использование стандартных множителей (коэффициентов) наращения и дисконтирования стоимости (приложения 1-4) существенно ускоряет и облегчает процесс оценки стоимости денег во времени.

4.2. КОНЦЕПЦИЯМ МЕТОДИЧЕСКИЙ У. ИНСТРУМЕНТАРИЙ УЧЕТА

ФАКТОРА ИНФЛЯЦИИ

В процессе управления прибылью постоянно приходится считаться с фактором инфляции, которая с течением времени обесценивает стоимость находящихся в обращении денежных средств (капитала в денежной форме).

Влияние инфляции сказывается на многих аспектах хозяйственной деятельности предприятия. В процессе инфляции происходит относительное занижение стоимости отдельных материальных активов, используемых предприятием (основных средств, запасов товарно-материальных ценностей и т.п.); снижение реальной стоимости денежных и других финансовых его активов (дебиторской задолженности, нераспределенной прибыли, инструментов финансового инвестирования и т.п.); занижение себестоимости производства продукции, вызывающее искусственный рост суммы прибыли и приводящее к росту налоговых отчислений с нее; падение реального уровня предстоящих инвестиционных доходов предприятия и т.п. Особенно сильно фактор инфляции сказывается на проведении долгосрочных финансовых и инвестиционных операций предприятия.

Инфляция является объективным, постоянно действующим фактором, присущим развитию экономики не только нашей страны, но практически всех стран мирового сообщества. Даже в странах с развитой и наиболее устойчивой экономикой — США, Японии, ФРГ, Великобритании, Франции и других — инфляционные процессы происходят непрерывно, хотя их интенсивность относительно низкая. В современной экономической теории принято даже считать, что рост уровня цен в пределах 10% в год является нормальным экономическим явлением, оказывающим стимулирующее воздействие на развитие общественного производства.

Стабильность проявления фактора инфляции и его активное воздействие на результаты хозяйственной деятельности предприятия определяют необходимость постоянного учета влияния этого фактора в процессе управления прибылью.

Концепция учета влияния фактора инфляции в управлении различными аспектами хозяйственной деятельности предприятия заключается в необходимости реального отражения стоимости его активов и денежных потоков, а также в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами, при осуществлении различных хозяйственных операций.

Реализация этой концепции в практике управления прибылью и использование соответствующего ее методического инструментария требуют предварительного рассмотрения ряда связанных с ней базовых понятий. Ниже изложено содержание основных из этих понятий.

ИНФЛЯЦИЯ — процесс постоянного превышения темпов роста денежной массы над товарной (включая стоимость услуг), в результате чего происходит переполнение каналов обращения деньгами, сопровождающееся их обесценением и ростом цен.

ТЕМП ИНФЛЯЦИИ — показатель, характеризующий размер обесценения (снижения покупательной способности) денег в определенном периоде, выраженный приростом среднего уровня цен в процентах к их номиналу на начало периода.

ФАКТИЧЕСКИЙ ТЕМП ИНФЛЯЦИИ - показатель, характеризующий реальный прирост среднего уровня цен в рассматриваемом прошедшем периоде.

ОЖИДАЕМЫЙ ТЕМП ИНФЛЯЦИИ - прогнозный показатель, характеризующий возможный прирост среднего уровня цен в рассматриваемом предстоящем периоде.

ИНДЕКС ИНФЛЯЦИИ — показатель, характеризующий общий рост уровня цен в определенном периоде, определяемый путем суммирования базового их уровня на начало периода (принимаемого за едини-

Раздел I. Концептуальные основы управления прибылью предприятия

цу) и темпа инфляции в рассматриваемом периоде (выраженного десятичной дробью).

НОМИНАЛЬНАЯ СУММА ДЕНЕЖНЫХ СРЕДСТВ -оценка размеров денежных активов в соответствующих денежных единицах без учета изменения покупательной стоимости денег в рассматриваемом периоде.

РЕАЛЬНАЯ СУММА ДЕНЕЖНЫХ СРЕДСТВ - оценка размеров денежных активов с учетом изменения уровня покупательной стоимости денег в рассматриваемом периоде, вызванного инфляцией.

НОМИНАЛЬНАЯ ПРОЦЕНТНАЯ СТАВКА - ставка процента, устанавливаемая без учета изменения по-: купательной стоимости денег в связи с инфляцией (или общая процентная ставка, в которой не элиминирована ее инфляционная составляющая).

РЕАЛЬНАЯ ПРОЦЕНТНАЯ СТАВКА - ставка процента, устанавливаемая с учетом изменения покупательной стоимости денег в рассматриваемом периоде в связи с инфляцией.

ИНФЛЯЦИОННАЯ ПРЕМИЯ — дополнительный доход, выплачиваемый (или предусмотренный к выплате) инвестору с целью возмещения финансовых потерь от обесценения денег в связи с инфляцией. Уровень этого дохода обычно приравнивается к темпу инфляции.

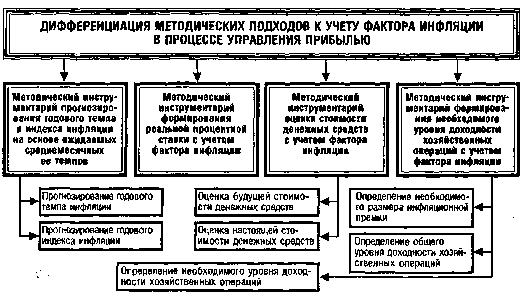
С учетом рассмотренных базовых понятий формируется конкретный методический инструментарий, позволяющий учесть фактор инфляции в процессе управления прибылью предприятия. Этот методический инструментарий дифференцируется в разрезе следующих основных вычислений (рис. 4.7.).

I. Методический инструментарий прогнозирования годового темпа и индекса инфляции основывается на ожидаемых среднемесячных ее темпах. Такая информация содержится в публикуемых прогнозах экономического и социального развития страны на предстоящий период. Результаты прогнозирования служат основой последующего учета фактора инфляции в хозяйственной деятельности предприятия.

где ТИг — прогнозируемый годовой темп инфляции, выраженный десятичной дробью; ТИм—ожидаемый среднемесячный темп инфляции в предстоящем периоде, выраженный десятичной дробью.

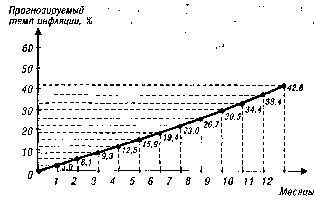
Пример: Необходимо определить годовой темп инфляции, если в соответствии с прогнозом экономического и социального развития страны (или собственными прогнозными расчетами) ожидаемый среднемесячный темп инфляции определен в размере 3%. Подставляя это значение в формулу, получим: Прогнозируемый годовой темп инфляции составит: (1 + 0,003)¹² -1 = 1,4258 - 1 = 0,4258 или 42,58%. По указанной формуле может быть рассчитан не только прогнозируемый годовой темп инфляции, но и значение этого показателя на конец любого месяца предстоящего года. Это может быть проиллюстрировано графически исходя из условия рассмотренного примера (рис. 4.8.).

Рисунок 4.7. Систематизация основных методических подходов к учету фактора инфляции в процессе управления прибылью предприятия. 1. При прогнозировании годового темпа инфляции используется следующая формула: ТИГ= (1 + ТИЧ)'2 - I ,

Рисунок 4.8 Результаты расчета темпа инфляции (в %) с начала предстоящего года исходя из ожидаемого среднемесячного ее темпа в размере 3%. 2. При прогнозировании годового индекса инфляции используются следующие формулы:

ИИ_Г =1 + ти<sub>г

ШИ</sub>^ИИ' ⁼ (1 ⁺ ТИм)¹² .

где ИИГ—прогнозируемый годовой индекс инфляции, выраженный десятичной дробью; ТИГ —прогнозируемый годовой темп инфляции, выраженный десятичной дробью (рассчитанный по ранее приведенной формуле); ТИМ — ожидаемый среднемесячный темп инфляции, выраженный десятичной дробью. Пример: Исходя из условий предыдущего примера, необходимо определить прогнозируемый годовой индекс инфляции.

Онравен: 1 + 0,4258 = 1,4258 (или 142,6%); или (1 + 0,03)¹² = 1,4258 (или 142,6%).

II. Методический инструментарий формирования реальной процентной ставки с учетом фактора инфляции

основывается на прогнозируемом номинальном ее уровне на финансовом рынке (результаты такого прогноза отражены обычно в ценах фьючерсных и опционных контрактов, заключаемых на фондовой бирже) и результатах прогноза годовых темпов инфляции. В основе расчета реальной процентной ставки с учетом фактора инфляции лежит Модель Фишера, которая имеет следующий вид:

1 -ТИ ^р_ 1 + ТИ ’

где /_р —реальная процентная ставка (фактическая или прогнозируемая в определенном периоде), выраженная десятичной дробью; /—номинальная процентная ставка (фактическая или прогнозируемая в определенном периоде), выраженная десятичной дробью; ТИ-темп инфляции (фактический или прогнозируемый в определенном периоде), выраженный десятичной дробью.

Пример: Необходимо рассчитать реальную годовую процентную ставку на предстоящий год с учетом следующих данных:

..'. - номинальная годовая процентная ставка по опционным и фьючерсным операциям на фондовой бирже на предстоящий год сложилась в размере 19%; прогнозируемый годовой темп инфляции составляет 7%.

Подставляя эти данные в Модель Фишера получим: реальная годовая процентная ставка

0,19-0,07 1 + 0,07

=0,112

(или 11,2%)

прогнозируется в размере:

III. Методический инструментарий оценки стоимости денежных средств с учетом фактора инфляции позволяет осуществлять расчеты как будущей, так и настоящей их стоимости с соответствующей "инфляционной составляющей". В основе осуществления этих расчетов лежит формируемая реальная процентная ставка.

1. При оценке будущей стоимости денежных средств с учетом фактора инфляции используется следующая формула (представляющая собой модификацию рассмотренной ранее Модели Фишера):

5_Н - Р х [(1 + /_р) х (I + ТИ)]*_;

где Sh — номинальная будущая стоимость вклада (денежных средств), учитывающая фактор инфляции; ; Р— первоначальная сумма вклада;

/р — реальная процентная ставка, выраженная де-* сятичной дробью;

ТИ — прогнозируемый темп инфляции, выраженный десятичной дробью; п — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Пример: Определить номинальную будущую стоимость вклада с учетом фактора инфляции при следующихусловиях:

первоначальная сумма вклада составляет 1000уел. ден. ед.;

реальная годовая процентная ставка, используемая для наращения стоимости вклада, составляет 20%; прогнозируемый годовой темп инфляции составляет 12%;

общий период размещения вклада составляет 3 года при начислении процента один раз в

год.

Подставляя эти показатели в вышеприведенную формулу, получим:

номинальная будущая стоимость вклада, учитывающая фактор инфляции, — =1000 х [(1 + 0,20) х(1 + 0,12)]³ = 2428усл. ден. ед.

2. При оценке настоящей стоимости денежных средств с учетом фактора инфляции используется следующая формула:

С

[(l + /_D)x(l+TH)r

P_rt=-

гд$ Рр — реальная ^{14 р/ v /J} настоящая сумма вклада (денежных средств), учитывающая фактор инфляции; 5"н — ожидаемая номинальная будущая стоимость

вклада (денежных средств); /р — реальная процентная ставка, используемая в процессе дисконтирования стоимости, выраженная десятичной дробью; ТИ — прогнозируемый темп инфляции, выраженный десятичной дробью; и — количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Пример: Необходимо определитьреальную настоящую стоимость денежных средств при следующих условиях:

ожидаемая номинальная будущая стоимость денежных средств составляет 1000 уел. ден. ед. реальная процентная ставка, используемая в процессе дисконтирования стоимости, составляет 20% в год; прогнозируемый годовой темп инфляции составляет 12%;

период дисконтирования составляет 3 года, а его интервал — 1 год.

Подставляя эти показатели в вышеприведенную формулу, получим:

реальная настоящая сумма денежных средств, учитывающая фактор инфляции, =

1000

= -- =412'

f(l+0,20):<(ly.0,12)] уел. ден. единиц.

4. Методический инструментарий формирования необходимого уровня доходности инвестиционных операций с учетом фактора инфляции, с одной стороны, призван обеспечить расчет суммы и уровня "инфляционной премии", а с другой — расчет общего уровня номинального дохода, обеспечивающего возмещение предприятию инфляционных потерь и получение необходимого уровня реальной прибыли.

1. При определении необходимого размера инфляционной премии используется следующая формула:

n_tt=Px ТИ,

где П_и — сумма инфляционной премии в определенном периоде; Р — первоначальная стоимость денежных средств; ТИ — темп инфляции в рассматриваемом периоде, выраженный десятичной дробью.

Пример: Рассчитатьразмер годовой инфляци-1^: > онной премии при следующихусловиях: первоначальная стоимость денежных средств составляет 1000уел. ден. ед.; прогнозируемый годовой темп инфляции составляет 12%.

Подставляя эти значения в формулу, получим: сумма инфляционной премии составляет = = 1000 х 0,12 = 120 уел. ден. ед. (уровень инфляционной премии приравнивается к темпу инфляции).

2. При определении общей суммы необходимого дохода по инвестиционной операции с учетом фактора инфляции используется следующая формула:

Дн = Др + П_и,

где Дн — общая номинальная сумма необходимого дохода по хозяйственной операции с учетом фактора инфляции в рассматриваемом периоде; Др — реальная сумма необходимого дохода по инвестиционной операции в рассматриваемом периоде, исчисленная по простым или сложным процентам с использованием реальной процентной ставки;

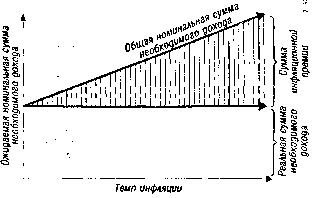
-in П_и — сумма инфляционной премии в рассматриваемом периоде. Зависимость общей суммы необходимого дохода и размера инфляционной премии от темпа инфляции может быть представлена графически (рисунок 4.9).

Рисунок 4.9. Зависимость номинальной суммы необходи-..;и-. - , мого дохода и размера инфляционной премии 4 от темпа инфляции. 3. При определении необходимого уровня доходности хозяйственных операций с учетом фактора инфляции используется следующая формула:

^УД"⁼дГ‘ .

где УДн — необходимый .. ^р уровень доходности хозяйственных операций с

учетом фактора инфляции, выраженный десятичной дробью;

Д_н — общая номинальная сумма необходимого дохода по хозяйственной операции в рассматриваемом периоде.

Др — реальная сумма необходимого дохода по хозяйственной операции в рассматриваемом периоде.

Следует отметить, что прогнозирование темповинфляции представляет собой довольно сложный и трудоемкий вероятностный процесс, в значительной степени подверженный влиянию субъективных факторов.Поэтому в практике управления прибылью может бытьиспользован более простой способ учета фактора инфляции. В этих целях стоимость денежных средств приих последующем наращении или размер необходимого дохода при последующем его дисконтировании пере-считывается заранее из национальной валюты в однуиз "сильных" (т.е. в наименьшей степени подверженных инфляции) свободно конвертируемых валют по курсуна момент проведения расчетов. Процесс наращения илидисконтирования стоимости осуществляется затем пореальной процентной ставке (минимальной реальнойнорме прибыли на капитал). Такой способ оценки настоящей или будущей стоимости необходимого доходапозволяет вообще исключить из ее расчетов факторинфляции внутри страны.

4.3. КОНЦЕПЦИЯ. И МЕТОДИЧЕСКИЙ ИНСТРУМЕНТЛРИЙУЧЕТЛ

ФАКТОРА РИСКА

Риски, сопровождающие хозяйственную деятельность, формируют обширный портфель рисков предприятия, который определяется общим понятием — предпринимательский риск. Его уровень возрастает с расширением объема и диверсификацией хозяйственной деятельности, со стремлением менеджеров повысить уровень доходности операций, с освоением инновационных технологий и инструментов.

Предпринимательский риск оказывает серьезное влияние на многие аспекты хозяйственной деятельности предприятия, однако наиболее значимое его влияние проявляется в двух направлениях: 1) уровень риска оказывает определяющее воздействие на формирование уровня прибыльности хозяйственных операций предприятия — эти два показателя находятся в тесной взаимосвязи и представляют собой единую систему "доходность — риск"; 2) предпринимательский

риск является основной формой генерирования прямой угрозы банкротства предприятия, так как финансовые потери, связанные с этим риском, являются довольно ощутимыми.

Риски, сопровождающие хозяйственную деятельность, являются объективным, постоянно действующим фактором в функционировании любого предприятия и поэтому требуют серьезного внимания со стороны руководства и менеджеров. Учет фактора риска в процессе управления хозяйственной деятельностью предприятия сопровождает подготовку практически всех управленческих решений.

Концепция учета фактора риска состоит в объективной оценке его уровня с целью обеспечения формирования необходимого уровня прибыльности хозяйственных операций и разработки системы мероприятий, минимизирующих его негативные финансовые последствия для хозяйственной деятельности предприятия.

Использование соответствующего методического инструментария учета фактора риска в хозяйственной деятельности предприятия требует предварительного рассмотрения базовых понятий в этой области. Ниже рассматриваются основные базовые понятия, связанные с учетом фактора риска.

РИСК — возможность наступления неблагоприятного события, связанного с различными видами потерь.

ИНДИВИДУАЛЬНЫЙ ХОЗЯЙСТВЕННЫЙ РИСК -

риск, присущий отдельным хозяйственным операциям предприятия, или отдельным финансовым инструментам, используемым им в процессе хозяйственной деятельности.

ПОРТФЕЛЬНЫЙ ХОЗЯЙСТВЕННЫЙ РИСК - общий риск, присущий сформированной совокупности финансовых инструментов инвестирования. Основными видами портфельного риска на предприятии могут выступать: риск фондового портфеля (сформированной совокупности ценных бумаг); риск депозитного портфеля (сформированной совокупности депозитных счетов предприятия в коммерческих банках) и другие.

СИСТЕМАТИЧЕСКИЙ (РЫНОЧНЫЙ) РИСК - риск, связанный с изменением конъюнктуры всего финансового рынка (или отдельных его сегментов) под влиянием макроэкономических факторов. Он возникает для всех участников этого рынка и не может быть устранен ими в индивидуальном порядке.

НЕСИСТЕМАТИЧЕСКИЙ (СПЕЦИФИЧЕСКИЙ) РИСК -совокупная

характеристика внутренних рисков, присущих деятельности конкретных хозяйствующих субъектов (эмитентов ценных бумаг, дебиторов и т.п.).

БЕЗРИСКОВАЯ НОРМА ДОХОДНОСТИ - норма доходности по хозяйственным операциям, по которым отсутствует реальный риск потери капитала или дохода. Этот показатель используется обычно как основа расчета необходимой нормы доходности по хозяйственным операциям с учетом премии за риск.

БЕЗРИСКОВЫЕ ХОЗЯЙСТВЕННЫЕ ОПЕРАЦИИ -

хозяйственные операции, по которым отсутствует реальный риск потери капитала или дохода и гарантировано получение расчетной реальной суммы инввестиционной прибыли.

УРОВЕНЬ РИСКА — показатель, характеризующий вероятность возникновения определенного вида риска и размер возможных финансовых потерь при его реализации.

СООТНОШЕНИЕ УРОВНЯ ДОХОДНОСТИ И РИСКА -одна из основных базовых концепций управления прибылью, определяемая прямой взаимосвязью этих двух показателей. В соответствии с этой концепцией рост уровня доходности хозяйственных операций при прочих равных условиях всегда сопровождается повышением уровня их риска и наоборот. Конкретные количественные соотношения на шкале "доходность — риск" определяются "Ценовой Моделью Капитальных Активов".

ВЕРОЯТНОСТЬ РИСКА — измеритель частоты возможного наступления неблагожелательного случая в процессе хозяйственной деятельности, вызывающего финансовые потери предприятия.

БЕТА-КОЭФФИЦИЕНТ (или бета) — показатель, характеризующий уровень изменчивости курса котировки

отдельного инвестиционного инструмента (ценной бумаги) или их портфеля по отношению к динамике сводного индекса цен всего инвестиционного (фондового) рынка. Бета-коэффициент измеряет уровень как индивидуального, так и портфельного систематического риска. Чем выше значение бета-коэффициента, тем выше уровень систематического и общего риска по конкретному инвестиционному инструменту или их портфелю в целом.

ЦЕНОВАЯ МОДЕЛЬ КАПИТАЛЬНЫХ АКТИВОВ - модель определения необходимого уровня доходности отдельных инвестиционных (фондовых) инструментов с учетом уровня их систематического риска, . измеряемого с помощью бета-коэффициента. Расчетный механизм этой модели учитывает необходимый размер премии за риск.

ПРЕМИЯ ЗА РИСК — дополнительный доход, выплачиваемый (или предусмотренный к выплате) предприятию сверх того уровня, который может быть получен по безрисковым хозяйственным операциям. Этот дополнительный доход должен возрастать про-^л , порционально увеличению уровня систематического риска по конкретному финансовому (фондовому) ; инструменту. Основой определения этой количественной зависимости является график "Линии надежности рынка".

"ЛИНИЯ НАДЕЖНОСТИ РЫНКА" - графический метод определения зависимости между уровнем систематического риска по конкретному фининсовому инструменту (ценной бумаге) и уровнем необходимой доходности по нему (этот график будет приведен и рассмотрен при изложении соответствующего раздела методического инструментария учета фактора риска).

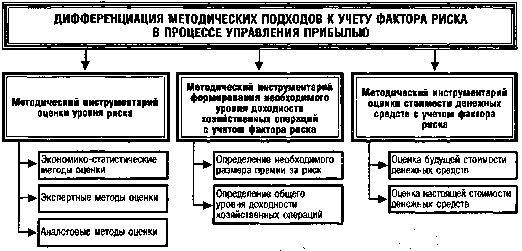
С учетом рассмотренных базовых понятий формируется конкретный методический инструментарий учета фактора риска, позволяющий решать связанные с ним конкретные задачи управления прибылью предприятия. Дифференциация этого методического инструментария отражает следующую систематизацию задач учета фактора риска в процессе хозяйственнойдеятельности (рис. 4.10.).

Рисунок 4.10. Систематизация основных методических подходов к учету фактора риска в процессе управления прибылью предприятия. I. Методический инструментарий оценки уровня риска является наиболее обширным, так как включает в себя разнообразные экономике-статистические,

экспертные, аналоговые методы осуществления такой оценки. Выбор конкретных методов оценки определяется наличием необходимой информационной базы и уровнем квалификации менеджеров.

1. Экономико-статистические методы составляют основу проведения оценки уровня риска. К числу основных расчетных показателей такой оценки относятся:

а) Уровень риска. Он характеризует общий алгоритмоценки этого показателя,

~ „ УР = ВР х РП ,

представленный следующеиформулои: ’

где УР — уровень соответствующего риска;

размер возможных

ВР — вероятность возникновения данного риска; РП — финансовых потерь при реализации данного риска.

В практике использования этого алгоритма размер возможных финансовых потерь выражается обычно абсолютной суммой, а вероятность возникновения риска — одним из коэффициентов измерения этой вероятности (коэффициентом вариации, бета-коэффициентом и др.) Соответственно уровень риска при его расчете по данному алгоритму будет выражен абсолютным показателем, что существенно снижает базу его сравнения при рассмотрении альтернативных вариантов.

б) Дисперсия. Она характеризует степень колеблемостиизучаемого показателя (в

данном случае — ожидаемогодохода от осуществления хозяйственной операции) поотношению к его средней величине. Расчет дисперсииосуществляется по следующей формуле:

и ²

с² = 1(Ъ-Ю XP_t,

1=1

где о² — дисперсия;

і?! — конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой хозяйственной операции; R— среднее ожидаемое значение дохода по рассматриваемой хозяйственной операции;

Pi — возможная частота (вероятность) получения отдельных вариантов ожидаемого дохода по хозяйственной операции п — число наблюдений.

в) Среднеквадратическое (стандартное) отклонение. Этот показатель является одним из наиболее распространенных при оценке уровня индивидуального хозяйственного риска, так же как и дисперсия определяющий степень колеблемости и построенный на ее основе. Он рассчитывается по следующей формуле:

о=^>,-я) хЧ.

где с — среднеквадратическое (стандартное) отклонение; Ri— конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой хозяйственной операции; R — среднее ожидаемое значение дохода по рассматриваемой хозяйственной операции; Pi — возможная частота (вероятность) получения отдельных вариантов ожидаемого дохода по хозяйственной операции; п — число наблюдений.

Пример: Необходимо оценитъуровенъриска по инвестиционной операции по следующим данным: нарассмотрение представлено два альтернативных ' инвестиционныхпроекта (проект "А"ипроект "Б")

.А, . с вероятностью ожидаемых доходов, представленной ¦ в табл. 4.2.

Сравнивая данные по отдельным инвестиционным \ проектам, можно увидеть, что расчетные величины доходов по проекту "А " колеблются в пределах от 200 до 600 уел. ден. ед. при сумме ожидаемых доходов в целом 450 уел. ден. ед. По проекту "Б" сумма ожидаемых доходов в целом также составляет 450 уел. ден. ед., однако их колеблемость осуществляется в диапазоне от 100 до 800 уел. ден. ед. Даже такое простое сопоставление позволяет сделать вывод о том, что риск реализации инвестиционного проекта "А" значительно меньше, чем проекта "Б", где колеблемостьрасчетного дохода выше.

Таблица 4.2. Распределение вероятности ожидаемых доходов по двум инвестиционным проектам

Возможные значения конъюнктуры инвестиционного рынка	Инвестиционный проект "А"	Инвестиционный проект "Б"
Расчетный доход, уел. Аі'іі /'/)_	Значение вероятности	Сумма ожидаемых доходов, уел.	Расчетный доход, уел.	Значение вероятности	Сумма ожидаемых доходов, уел.
Высокая	600	0,25	150	800	0,20	160
Средняя	500	0,50	250	450	0,60	270
Низкая	200	0,25	50	100	0,20	20
В целом	—	1,0	450	—	1,0	450

Более наглядное представление об уровне риска дают результаты расчета среднеквадратического (стандартного) отклонения, представленные в табл. 4.3.

Таблица 4.3. Расчет среднеквадратического (стандартного) отклонения по двум инвестиционным проектам

іі «1 к 3.S «5 &	Возможные значения конъюнктуры инвестиционного рынка	в,	я		[Rt~Rp	Л	(Ri~R)2* *Р,
)(RrRpx. і
3 Р §? «і а, 2 * Sч	Высокая Средняя Низкая	600 500 200	450 450 450	+150 +50 -250	22500 2500 62500	0,25 0,50 0,25	5625 1250 15625	—
В целом	—	450	—	—	1,00	22500	150
	Высокая	800	450	+550	122500	0,20	24500
§4t	Средняя	450	450	0	0	0,60	0	—
P s	Низкая	100	450	-350	122500	0,20	24500	—
8 5"	В целом	—	450	—		1,00	49000	221

Результаты расчета показывают, что средне-квадратическое (стандартное) отклонение по инвестиционному проекту "А" составляет 150, в то время как по инвестиционному проекту "Б " — 221, что свидетельствует о болъшемуровне его риска.

Рассчитанные показатели среднеквадратиче-ского (стандартного) отклонения по рассматриваемым инвестиционным проектам могут быть интерпретированы графически (рис. 4.11.)



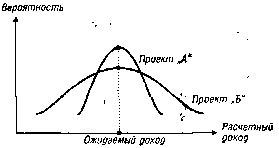
Рисунок 4.11. Распределение вероятности ожидаемого (расчетного) дохода по двум инвестиционным проектам.

Из графика видно, чтораспределение вероятностей проектов "А"и "Б"имеют одинаковую величину расчетного дохода, однако в проекте "А " кривая уже, что свидетельствует о меньшей колеблемости вариантов расчетного дохода относительно средней его величины R, а следовательно и о меньшемуровнериска этого проекта.

г) Коэффициент вариации. Он позволяет определить уровень риска, если показатели среднего ожидаемого дохода от осуществления хозяйственных операций различаются между собой. Расчет коэффициента вариации осуществляется по следующей формуле:

С? ~^=

R ’

где CV— коэффициент вариации;

а — среднеквадратическое (стандартное) отклонение; R — среднее ожидаемое значение дохода по рассматриваемой хозяйственной операции. Пример: Необходимо рассчитать коэффициент вариации по трем инвестиционным проектам при различных значениях среднеквадратического (стандартного) отклонения и среднего ожидаемого значения дохода по ним. Исходные данные ирезулътаты расчета приведены в табл. 4.4. Таблица 4.4. Расчет коэффициента вариации по трем

инвестиционным проектам

Варианты проектов	Среднеквадра тическое (стандартно е)	Средний ожидаемый доход по проекту, R	Коэффициен т вариации,
Проект "А" Проект "Б" Проект ”В"	150 221 318	450 450 600	0,33 0,49 0,53

Результаты расчета показывают, что наименьшее значение коэффициента вариации — по проекту "А", а наибольшее — по проекту "В". Таким образом, хотя ожидаемый доход по проекту "В" на 33% выше, чем по проекту "А"уровенъ

ХІ00

/'600-450

j ’коэффициентом вариации, выше на

450

риска по нему, определяемый V

61%о

Гадз-Мхіоо].

Следовательно, ? ) при сравнении уровней рисков по отдельным

инвестиционным проектам предпочтение при прочих равных условиях следует отдавать тому из них, по которому значение коэффициентов вариации самое низкое (что свидетельствует о наилучшем соотношении доходности и риска).

д) Бета-коэффициент (или бета). Он позволяет оценить индивидуальный или портфельный систематический финансовый риск по отношению к уровню риска финансового рынка в целом. Этот показатель используется обычно для оценки рисков

инвестирования в отдельные ценные бумаги. Расчет этого показателя осуществляется по формуле:



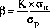
где р —бета-коэффициент;

К —степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом;

о"и — среднеквадратическое (стандартное) отклонение доходности по индивидуальному виду ценных бумаг (или по их портфелю в целом);

с_р —среднеквадратическое (стандартное) отклонение доходности по фондовому рынку в целом.

Уровень риска отдельных ценных бумаг определяется на основе следующих значений бета-коэффициентов:

B = 1 — средний уровень; B > 1 — высокий уровень; B < 1 — низкий уровень.

2. Экспертные методы оценки уровня риска применяются в том случае, если на предприятии отсутствуют необходимые информативные данные для осуществления расчетов экономико-статистическими методами. Эти методы базируются на опросе квалифицированных специалистов (страховых, финансовых, инвестиционных менеджеров соответствующих специализированных организаций) с последующей математической обработкой результатов этого опроса.

В целях получения более развернутой характеристики уровня риска по рассматриваемой операции опрос следует ориентировать на отдельные виды рисков, идентифицированные по данной операции (процентный, валютный и т.п.).

В процессе экспертной оценки каждому эксперту предлагается оценить уровень возможного риска, основываясь на определенной балльной шкале, например: риск отсутствует: 0 баллов;

риск незначительный: 10 баллов;

риск ниже среднего уровня: 30 баллов; риск среднего уровня: 50 баллов;

риск выше среднего уровня: 70 баллов;

МЛ. Бланк

риск высокий: 90 баллов;

риск очень высокий: 100 баллов.

3. Аналоговые методы оценки уровня риска позволяют определить уровень рисков по отдельным наиболее массовым хозяйственным операциям предприятия. При этом для сравнения может быть использован как собственный, так и внешний опыт осуществления таких хозяйственных операций.

II. Методический инструментарий формирования необходимого уровня доходности хозяйственных операций с учетом фактора риска позволяет обеспечить четкую количественную пропорциональность этих двух показателей в процессе управления хозяйственной деятельностью предприятия.

1. При определении необходимого уровня премии за риск используется следующая формула:

где RP_n —уровень премии за риск по конкретному финансовому (фондовому) инструменту; R_n— средняя норма доходности на финансовом

рынке; А_п — безрисковая норма доходности на финансовом рынке; (3 — бета-коэффициент, характеризующий уровень систематического риска по конкретному финансовому (фондовому) инструменту. Пример: Необходимо рассчитать уровень премии за риск по трем видам акций. Исходные данные ирезультатырасчета приведены в табл. 4.5.

Таблица 4.5. Расчет необходимого уровня премии за риск по трем акциям

В арианты акций	Ср едняя норма дох	Безр исковая норма доходности на	ета- коэффиц	Урове нь прем
А кция 1 Акция 2	12 ,0 12,0 12,0	5,0 5,0 5,0	,8 1,0 1,2	5,6 7,0 8,4

Результаты расчета показывают, что уровень премии за риск возрастает пропорционально росту бета-коэффициента, т.е. уровня систематического риска.

2. При определении необходимой суммы премии за риск используется следующая формула:

RP_S = SI у. RP_n ,

где RP_S — сумма премии за риск по конкретному финансовому (фондовому) инструменту в настоящей стоимости; SI—стоимость (котируемая цена) конкретного финансового (фондового) инструмента; RP_n— уровень премии за риск по конкретному финансовому (фондовому) инструменту, выраженный десятичной дробью.

Пример: Исходя из котируемой цены трех акций на фондовом рынке и результатов расчета уровня премии за риск по ним (см. предыдущий пример) определить сумму этой премии по каждой акции. Исход- ные данные и результаты расчета представлены в табл. 4.6.

Таблица 4.6. Расчет необходимой суммы премии за риск по трем акциям

Варианты акций	Котируемая цена акций на фондовом рынке,	Уровень премии за риск	Сумма премии за риск (определенная
Акция 1	100	0,056	5,6 4,9 7,6
Акция 2	70 90	0,070
Акция 3		0,084

3. При определении (необходимого) общего уровня доходности хозяйственной операции с учетом фактора риска используется следующая формула:

RD„ = А_п + RP„ _t

где RD_n — общий уровень доходности го» конкретномуфинансовому (фондовому) инструменту с учетом фактора риска; ,< >¦

А„ — безрисковая норма доходности на финансовом рынке; RP_n — уровень премии за риск по конкретному финансовому (фондовому) инструменту. При определении уровня избыточной доходности (премии за риск) всего портфеля ценных бумаг на единицу его риска используется "коэффициент Шарпа", определяемый по следующей формуле:

_Г RDp — Ап

^Sp ~ g{RD_p-A)’

где ^Л — коэффициент Шарпа, измеряющий избыточ-* /> ную доходность портфеля на единицу риска, характеризуемую среднеквадратическим (стандартным) отклонением этой избыточной доходности; RD_p — общий уровень доходности портфеля; Aw—уровень доходности по безрисковому финансовому инструменту инвестирования; s — среднеквадратическое отклонение избыточной доходности.

Пример: Следует рассчитать необходимый общий уровень доходности по трем видам акций. Исходные данные и резулътатырасчета приведены в табл. 4.7.

Таблица 4.7. Расчет необходимого общего уровня доходности по

трем акциям

Варианты акций	Безрисковая норма доходности на фондовом	Уровень премии за риск, %	Необходимый общий уровень доходности (определенный по
Акция 1 Акция 2 Акция 3	5,0 5,0 5,0	5,6 7,0 8,4	10,612,013,4

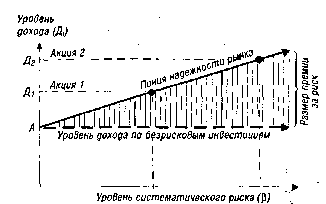
Изложенный выше методический инструментарий формирования необходимого уровня доходности хозяйственных операций с учетом фактора риска построен на "Ценовой Модели Капитальных Активов", разработанной Г. Марковицем и У. Шарпом (за разработку этой Модели они были удостоены в 1990 году Нобелевской премии). Графическую интерпретацию этой Модели составляет график "Линии надежности рынка" (рис. 4.12.)-

Рисунок 4.12. График „Линии надежности рынка". Отдельные точки на "Линии надежности рынка" показывают необходимый уровень доходности по ценной бумаге (с учетом премии за риск) в зависимости от уровня систематического риска по ней, измеряемого бета-коэффициентом. III. Методический инструментарий оценки стоимости денежных средств с учетом фактора риска дает возможность осуществлять расчеты как будущей, так и настоящей их стоимости с обеспечением необходимого уровня премии за риск. 1. При оценке будущей стоимости денежных средств с учетом фактора риска используется следующая формула:

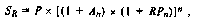
где Sr — будущая стоимость вклада (денежных средств), учитывающая фактор риска; Р — первоначальная сумма вклада;

А„ — безркековая норма доходности на финансовом рынкз, выраженная десятичной дробью; - RP„—уровень премии за риск по конкретному финансовому инструменту, выраженный десятичной дробью; п —количество интервалов, по которым осуществляется каждый конкретный платеж, в общем обусловленном периоде времени.

Пример; Необходимо определить будущую стоимость вклада с учетом фактора риска при следую-i щих условиях:

первоначальная сумма вклада составляет 1000 уел. ден. ед.;

безрисковая норма доходности на финансовомрынке составляет 5%;

уровень премии зариск определен в размере 7%; общий период размещения вклада составляет 3 года при начислении процента один раз в год.

Подставляя эти показатели в вышеприведенную формулу, получим:

будущая стоимость вклада, учитывающая фактор риска = = 1000 х 1(1 + 0,05) х (1 + 0,07)Р = 1418усл. ден. ед.

2. При оценке настоящей стоимости денежных средств с учетом фактора риска используется следующая формула:

Р -

Е0+4і)х(і+ДРв)Р

где PR — настоящая стоимость вклада (денежных средств), учитывающая фактор риска; Sr — ожидаемая будущая стоимость вклада (денежных средств); А_п — безрисковая норма доходности на финансовом рынке, выраженная десятичной дробью; RP„ — уровень премии за риск по конкретному финансовому инструменту, выраженный десятичной дробью; я — количество интервалов, по которым осуществляется каждый конкретный платеж, в общем обусловленном периоде времени.

Пример: Необходимо определить настоящую стоимость денежных средств с учетом фактора риска при следующих условиях: ожидаемая будущая стоимость денежных средств — 1000уел. ден. ед.;

безрисковая норма доходности на финансовом рынке составляет 5%; уровень премии за риск определен в размере 7%; период дисконтирования составляет 3 года, а его интервал — 1 год.

Подставляя эти данные в вышеприведенную формулу, получим: настоящая стоимость денежных средств с учетом фактора писка =

....... 1000 _ял

=-г - 705 1

[(I+0,05)x(l + 0,07)f '

уел. ден. ед.

Проведенный обзор показывает, что методический инструментарий учета фактора риска в управлении прибылью предприятия является довольно обширным и позволяет решать многообразные задачи в этой сфере хозяйственной деятельности. Более глубокое изложение вопросов управления рисками рассматривается в специальных разделах.

Выше был рассмотрен методический инструментарий вычислений наиболее широко используемый в современной практике управления прибылью предприятия. Методический инструментарий расчетов отдельных специальных показателей рассматривается в последующих разделах.



Содержание раздела

---

---

Главная сайта

---