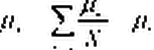Управление риском портфеля на основе анализа ковариаций активов

15.1. Введение.

В этой главе рассматриваются вопросы, связанные с оптимизацией портфеля активов. Изучается влияние корреляции между отдельными парами активов на общий риск портфеля, при этом в качестве меры риска принимается дисперсия (или среднеквадратичное отклонение). Рассказано о том, что такое эффективная диверсификация и как общий риск портфеля, составленного из произвольного количества активов, можно разделить на несистематический (диверсифицируемый) риск и рыночный (недиверсифицируемый) риск. Дано понятие границы эффективности на примере портфеля из двух активов и приведены формулы, которые позволяют выбрать на границе эффективности портфель с минимальным ожидаемым риском и портфель с максимальным отношением ожидаемого дохода к ожидаемому риску. Поставлена задача по оптимизации портфеля из произвольного количества активов с учетом ограничений на состав и веса активов в портфеле (лимитов), и приведен алгоритм поиска решений этой задачи методом Монте-Карло.

15.2. Корреляция активов и риск портфеля.

Результаты решения об инвестировании в тот или иной финансовый инструмент (актив) всегда имеют некоторую неопределенность. В большинстве случаев реально полученный доход от вложения в некий финансовый инструмент не совпадает с ожидаемым доходом по этому инструменту на момент принятия решения об инвестировании, то есть инвестирование - это сфера деятельности, связанная с риском.

Меру рассеяния реально полученных доходов относительно ожидаемого дохода, то есть риск актива, будем характеризовать дисперсией (или среднеквадратичным отклонением) доходов по данному активу.

Рассмотрим случай, когда инвестирование проводится в несколько активов (портфель). Портфель является линейной комбинацией активов, каждый из которых имеет собственное математическое ожидание дохода и дисперсию дохода.



Вспомним формулы для вычисления математического ожидания и дисперсии многомерной случайной величины у, являющейся линейной комбинацией коррелированных случайных величин:

N

у = I ^ak^xk

k=1

N

Му = I ^akMk

k =1

NN

2 2 ^ak^Gk

k=i

+ ²I I ^a,^akP,k^G,^Gk

k=1 i=k + 1

Поэтому для математического ожидания и дисперсии дохода портфеля активов можно использовать следующие формулы:

N

Му = I ^kMk

k=1

NN

+ ²1 I ^wi^wkPk^Gi^Gk

k=1

k=1 i=k+1

где w - веса активов в портфеле.

В отличие от произвольной линейной комбинации случайных

величин, веса активов подчиняются правилу нормирования:

N

I ^wk =¹

k=1

Следовательно:

- математическое ожидание дохода портфеля - это взвешенная сумма математических ожиданий доходов по отдельным активам,

- риск дохода портфеля - это взвешенная сумма ковариаций всех пар активов в портфеле, при этом вес каждой ковариации равен произведению весов соответствующей пары активов, а ковариация актива с самим собой является дисперсией данного актива.

15.3. Понижение риска портфеля. Диверсификация.

Из формулы для дисперсии портфеля активов очевидно, что риск портфеля можно разделить на две группы слагаемых.

223

Слагаемые вида w²k&k, которые характеризуют риск отдельных активов, всегда положительны. Следовательно они могут только увеличивать риск портфеля.

Слагаемые вида w_tw_kp_ika_iG_k, которые характеризуют ковариацию различных пар активов в портфеле, могут быть положительными, равными нулю и отрицательными. Все зависит от величины коэффициента корреляции между активами. Следовательно, эти слагаемые могут уменьшить риск портфеля в целом по сравнению с риском отдельных активов.

Проиллюстрируем этот эффект диверсификации на примере портфеля, состоящего из двух активов. Рассмотрим три случая, в каждом из которых математические ожидания и дисперсии активов одинаковы, а различными являются коэффициенты корреляции между ними:

1) Активы полностью коррелированны

В этом случае коэффициент корреляции между активами равен 1. Следовательно для дисперсии и с.к.о. портфеля получаем

2 22,22,0 ( , \2

^ = ^W1^1 + ^W2^2 + 2^W1^W2^1^2 =К^1 + ^W2^2 ⁾

Gy = ^W1&1 + ^W2&2

Следовательно, с.к.о. портфеля равно средней взвешенной с.к.о. отдельных активов, то есть понижение риска портфеля от диверсификации отсутствует.

2) Активы не коррелированны

Коэффициент корреляции между активами равен 0.

2 2 2, 2 2 ^y = ^W1^1 + ^W2^2

= V wV + w₂V₂²

В этом случае с.к.о. портфеля меньше средней взвешенной с. к. о. отдельных активов, то есть присутствует понижение риска портфеля от диверсификации, однако с.к.о. портфеля больше нуля при любых ненулевых дисперсиях отдельных активов.

3) Активы антикоррелированны

Коэффициент корреляции между активами равен -1.

224

2 2 2. 2 2 о ( Y

Gy = ^W1^G1 + ^W2 ^G 2 ^{- 2w}1^W2^G1^G2 = K^G1 ^{- W}2^G2 ⁾

G_y = |^W1^G1 ^{- w}2^2|

В этом случае эффект диверсификации наиболее значителен, с.к.о. портфеля может быть сведено к нулю соответствующим выбором весов отдельных активов в портфеле, то есть может быть получен безрисковый портфель.

Заметим, что во всех трех случаях математическое ожидание дохода портфеля одинаково и равно jU_y = w₁^₁ + w₂^₂.

Можно сказать, что эффективная диверсификация - это добавление таких активов в портфель, доходы по которым имеют наименьший коэффициент корреляции с активами, уже имеющимися в портфеле.

Рассмотрим теперь портфель, состоящий из большого количества активов N, каждый из которых входит в портфель с одинаковым весом 1/N. В случае более 2-х активов невозможно добиться того, чтобы каждая пара активов имела бы коэффициент корреляции, равный -1. Пусть все активы имеют вообще говоря различные конечные дисперсии и каждая пара активов имеет вообще говоря разные коэффициенты корреляции. Тогда формула для дисперсии портфеля примет вид:

^N 1 ₂ ^{N N} 1

G_y

= Еттг ^Gl + ²VV 772 PikGPk

k=1 ^ t?_г=k+1 n

Преобразуем эту формулу:

₂ 1 n gI N -1 ^{N N}

g~ = —"V —-^y NU N

G_k

N i=k+1 N(N -1)/2

Первая сумма - это средняя дисперсия активов, вторая (удвоенная) сумма - это средняя ковариация всех пар различных активов, следовательно:

1 —2 N -1 —

G =--G_k +---G_k

^y N ^k N

Поэтому, при достаточно большом количестве активов N первым слагаемым можно пренебречь и для дисперсии портфеля можно

написать приближенное выражение G²„ ~ G портфеля приближенно равна средней ковариации активов.

225

_y - „ _ik , то есть дисперсия

Таким образом, общий риск портфеля можно разделить на две части:

- несистематический риск, определяемый средней дисперсией активов, который может быть исключен путем формирования портфеля из большого количества активов (диверсификацией),

- систематический (рыночный) риск, определяемый средней ковариацией пар различных активов, который не может быть исключен путем формирования портфеля из большого количества активов (диверсификацией).

При этом математическое ожидание дохода портфеля равно среднему математическому ожиданию дохода входящих в портфель активов:

КТ

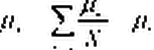
15.4. Граница эффективности.

В предыдущем параграфе было показано, что в случае, когда коэффициент корреляции между активами меньше 1, диверсификация портфеля может улучшить соотношение между ожидаемым доходом и ожидаемым риском. Это связано с тем, что ожидаемый доход портфеля является линейной комбинацией ожидаемых доходов по входящим в портфель активам, а дисперсия портфеля является квадратичной функцией от с.к.о. входящих в портфель активов.

При заданных математических ожиданиях и дисперсиях активов, а также коэффициентах корреляции между различными парами активов, путем оптимизации весов активов в портфеле можно добиться улучшения соотношения между доходом и риском портфеля.

Рассмотрим портфель, состоящий из двух активов, с коэффициентом корреляции между ними равным р = 0.5 :

- 1-й актив

ожидаемый доход /Л₁ = 10%

с.к.о. ожидаемого дохода (риск) и₁ = 15%

- 2-й актив

226

ожидаемый доход ?₂ = 13%

с.к.о. ожидаемого дохода (риск) и₂ = 16%

Ожидаемый доход и среднеквадратичное отклонение портфеля из двух активов вычисляются по формулам:

2 2 2 2 2

Vy = ^W^1 + ^2^2 ^у = ^W1^1 + ^w2^2 + ²P^W1 ^W2^2

Расчетные значения этих величин при различном соотношении весов активов представлены в таблице.

Вес 1-го актива	Вес 2-го актива	С.к.о. портфеля Доход портфеля
wi	W2	°у	Vy
0.0	1.0	16.00	13.00
0.1	0.9	15.21	12.70
0.2	0.8	14.54	12.40
0.3	0.7	14.01	12.10
0.4	0.6	13.64	11.80
0.5	0.5	13.44	11.50
0.6	0.4	13.41	11.20
0.7	0.3	13.56	10.90
0.8	0.2	13.89	10.60
0.9	0.1	14.37	10.30
1.0	0.0	15.00	10.00

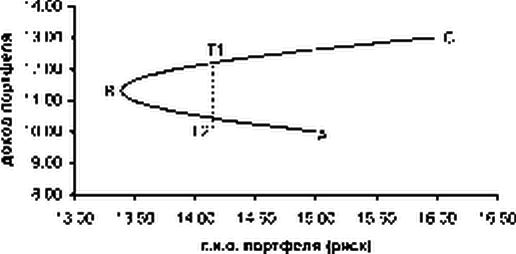
Зависимость ожидаемого дохода портфеля от с.к.о. портфеля (риска) приведена на рисунке

Граница эффективности

227

На линии АВС лежат все возможные комбинации дохода и риска портфеля. Точка А соответствует портфелю, состоящему только из 1-го актива, точка С соответствует портфелю, состоящему только из 2-го актива, точка В соответствует портфелю с наименьшим риском.

Аналитически координаты точки В в случае портфеля из 2-х активов можно найти из следующих соображений. Так как веса активов связаны соотношением w₂ = 1 — w₁, то математическое ожидание и дисперсию портфеля можно представить как функцию только от w₁:

My = ^WlMl + ^{(1 — w}i)^2

= wV + ^{(1 — w}i^{)2 CT}2² + ²P^wi ^{(1 — w}i ^2 Точку с минимальным значением дисперсии (с.к.о.) портфеля можно найти, взяв производную величины о²у по w₁ и приравняв ее к нулю. Решив уравнение относительно w₁ получим:

^w1 =

^G2 P^G1^G2

^G1 + ^G 2 ²P^G1^G 2

Подставив это выражение в формулы для р_у и <j_y, можно

g _y = 13.39%

найти ожидаемый доход и риск портфеля (с.к.о.) в точке В. Для рассмотренного здесь примера получим: wj = 0.56 w₂ = 0.44 р_у = 11.32%

Линия АВС:

- вогнута влево при коэффициенте корреляции р < 1, при этом вогнутость тем сильнее, чем меньше коэффициент корреляции,

- является отрезком прямой, соединяющим точки А и С, при коэффициенте корреляции р = 1.

Верхняя часть линии АВС (линия ВС) является границей эффективности. Линия ВС является эффективной в том смысле, что на ней невозможно повысить доход без повышения риска и снизить риск без снижения дохода (в отличие от линии АВ). Выше линии ВС находятся недостижимо привлекательные комбинации дохода и риска. Ниже линии ВС находятся худшие комбинации дохода и риска, которые могут быть улучшены

228

переходом на линию ВС. Например, переход из точки Т2 в точку Т1 приводит к увеличению дохода портфеля при неизменном уровне риска.

На границе эффективности не существует наилучшего портфеля. Выбор точки на этой линии зависит от инвестиционных предпочтений портфельного менеджера, то есть какую плату, выражаемую в единицах риска, он готов нести за добавочную единицу дохода.

Распространенным методом выбора точки на границе эффективности является выбор такого портфеля, для которого отношение ожидаемого дохода к ожидаемому риску является максимальным. Аналитически в случае портфеля из 2-х активов эту точку можно найти, приравняв к нулю производную по w₁ от функции

= ^WlA + ⁽¹ - ^Wl)^2

°y 4w²i°l + (1 - Wi)V₂² + 2/Ж’, (1 - Wi)<Ji<J₂

Решив полученное уравнение относительно w₁ найдем, что:

^wi =

P2P⁰1° 2 P'1⁰ 2

О1РТ1СТ2 ^- ^°1 ⁾ + ⁽М2Р°1°2 ^- М°2 ⁾

Для рассмотренного здесь примера точка с максимальным отношением дохода к риску:

w₁ = 0.37

о _y = 13.72%

p_v = 11.89%

w₂ = 0.63

15.5. Постановка задачи по оптимизации портфеля.

Под оптимизацией портфеля, состоящего из произвольного количества активов, мы будем понимать поиск таких наборов весов активов, которые обеспечивали бы:

- ожидаемый доход портфеля больший или равный наперед заданному минимальному значению дохода,

- ожидаемый риск портфеля меньший или равный наперед заданному максимальному значению риска.

Следовательно, если предполагаются известными ожидаемые доходы по каждому из активов, ожидаемые дисперсии (с.к.о.) дохода по каждому из активов, ковариации (коэффициенты кор

229

реляции) между каждой парой различных активов, то задача оптимизации портфеля сводится к тому, чтобы найти такие наборы весов активов, которые бы удовлетворяли системе

N

My = Z ^wkMk > Mmn

k=1

NN

+ ²Z ZwwPik°Pk — ^max

k=1 i=k+1

z

k=1

.2 2

a_y

N

Z w =¹

k=1

Будем предполагать, что в составе портфеля в качестве одного из активов могут находиться денежные средства, то есть безрисковый актив, имеющий нулевое ожидание дохода, нулевую дисперсию дохода и нулевой коэффициент корреляции с любым другим активом, поэтому равенство единице суммы весов всех активов является строгим.

Ожидаемый доход портфеля и ожидаемая дисперсия портфеля являются целевыми функциями. Целевые функции определяют задачу которая должна быть решена в процессе оптимизации. В данном случае задачей является максимизировать линейную функцию

M_y при одновременной минимизации квадратичной функции о²у с учетом заданных ограничении.

15.6. Введение ограничений на состав и веса активов в портфеле (лимитов).

В постановке задачи по оптимизации портфеля активов, сделанной в предыдущем параграфе, неявным образом предполагалось, что:

- портфельный менеджер имеет возможность инвестировать в любые активы, обращающиеся на рынке, то есть отсутствуют ограничения на состав активов в портфеле,

- отсутствуют ограничения на вес отдельного актива в портфеле.

Как правило присутствуют оба вида ограничений (лимиты). Дополним задачу оптимизации введением лимитов, то есть будем предполагать, что:

230

- в формулах для целевых функций присутствуют только разрешенные активы,

- вводятся ограничения на вес каждого конкретного актива в портфеле.

Ограничения на вес любого актива будем вводить как сверху, так и снизу. На практике низкое ограничение сверху вводят на потенциально очень доходные, но и очень рискованные активы. Самые низкие ограничения сверху вводят на веса активов, инвестиции в которые с высокой вероятностью могут быть потеряны полностью. В лучшем случае эти активы могут принести доход за пределами горизонта инвестирования. Ограничение сверху не может превышать 1. Ненулевые ограничения снизу вводятся как правило для создания в составе портфеля "подушки безопасности" из низкодоходных, но и низкорискованных активов. Ограничение снизу не может быть меньше 0. Кроме того, и набор ограничений сверху, и набор ограничений снизу имеют свои правила нормирования.

Итак, ограничения на веса активов в портфеле вводятся следующим образом:

W(min)k ^ Wk ^ W(max)k

0 ^ W(min)k < 1 0 < W(max)k ^ 1 N N Z W(min)k ^ 1 k=1 Z W(max)k ^ 1 k=1

15.7. Численное решение задачи оптимизации портфеля с учетом лимитов методом Монте-Карло.

Итак, задачу об оптимизации портфеля активов с учетом лимитов можно сформулировать в виде:

N

My = Z ^wkM_k > Ашп

k=1

NN

+²Z Zww prk°r°k

k=1 i=k+1

Z

k=1

2

max

2 2 ^wk°_k

N

^S = Z ^wk =¹

k=1

231

тивов
W(min)k — Wk — W(max)k
0 — W(min)k < 1	0 < W(max)k — 1
N	N
S(min) = ^ W(min)k — 1	S(max) = ^ W(max)k — 1
k=1	k=1

В этой задаче искомыми величинами являются наборы весов активов {w_k}, удовлетворяющие всем уравнениям и неравенствам. Решить такую задачу оптимизации аналитическими методами достаточно трудно, особенно в случае большого количества активов. Поэтому есть смысл попробовать найти ее решение численно методом Монте-Карло, генерируя случайным образом на компьютере удовлетворяющие ограничениям наборы весов активов и проверяя эти наборы на соответствие целевым функциям.

Разумеется, в конечной последовательности розыгрышей (генераций наборов весов) скорее всего не удастся найти все решения задачи оптимизации. Однако, каждое найденное решение будет удовлетворять всем условиям задачи, то есть портфель, построенный с помощью этого набора весов будет "достаточно оптимальным". Если решений будет несколько, из них можно выбрать то, при котором отношение ожидаемого дохода портфеля к ожидаемому риску будет максимальным.

Алгоритм решения задачи оптимизации

1) Задаем входные данные

1.1) Набор ожидаемых доходов по активам:

^{м К ^k = ^1,-_> ^N

1.2) Набор среднеквадратичных отклонений активов: ^{Ok^},^k = ¹,..., N

1.3) Набор коэффициентов корреляций между различными активами

^{Pik ^}

k = 1,..., N i = k +1,..., N

1.4) Минимально ожидаемый доход портфеля: /л_тт

232

1.5) Максимально ожидаемаый риск портфеля: cr_max

1.6) Набор ограничений снизу на веса активов:

^{W(mm)k }, ^k = ^1,-> ^N

1.7) Набор ограничений сверху на веса активов:

^{W(max)k ^{} k} = ¹>-_> ^N

1.8) Количество розыгрышей (генераций наборов весов): М

1.9) Точность нормирования (малое положительное число): 8

2) Задаем стартовое значение номера текущего розыгрыша m = 0

3) Номер текущего розыгрыша m = m +1

4) Разыгрываем случайным образом набор весов, соответствующий набору ограничений на веса активов

4.1) Задаем начальные минимально возможные значения весов

^Wk = ^W(min)k , ^k = ^1,-_> ^N

4.2) Вычисляем текущую сумму весов

N

^S = 2

k=1

4.3) k = 0

4.4) k = k +1

4.5) Разыгрываем приращение веса к-го актива dW = СЛУЧАЙНОЕ _ ЧИСЛО(0,

МИНИМУМ (1 - S, W(m_ax)k - W ))

4.6) Вычисляем текущий вес к-го актива w_k = w_k + dW

4.7) Вычисляем текущую сумму весов

S=S+dW

4.8) Если k<N, то переходим на шаг 4.4

4.9) Если не соблюдается точность нормирования, то

есть (1 - S) > 8, то переходим на шаг 4.3

233

5) Проверяем, соответствует ли портфель, составленный из полученных на шаге 4 весов, ограничениям на минимально ожидаемый доход и максимально ожидаемый риск портфеля

N

Му = 2 ^WMk > Mmin

к=1

NN

+²22^Wi^WkРгк°г°к

к=1 i=k+1

2

max

2 w,4²

k=1

и„

Если решение соответствует этим неравенствам, то фиксируем его, то есть запоминаем текущий набор весов и соответствующие ему ожидаемый доход, ожидаемый риск, отношение дохода к риску. Текущий розыгрыш за номером т завершен.

6)

7)

Если номер текущего розыгрыша m меньше, чем общее число розыгрышей М, то переходим на шаг 3

После того, как сделаны все розыгрыши (то есть т=М), среди всех найденных решений выбираем то, при котором отношение ожидаемого дохода портфеля к ожидаемому риску портфеля будет максимальным.

Если не было найдено ни одного решения, то необходимо:

- либо увеличить количество розыгрышей,

- либо ослабить ограничения по целевым функциям, то есть уменьшить ожидаемый доход и/или увеличить ожидаемый риск портфеля,

- либо пересмотреть ограничения на веса активов в портфеле в сторону расширения интервалов разрешенных значений весов.

Пример решения задачи оптимизации

Рассмотрим портфель, состоящий из трех активов:

- 1-й актив ожидаемый доход 10%

с.к.о. ожидаемого дохода (риск) 15% отношение доход/риск = 0.67 минимальный вес в портфеле 0 максимальный вес в портфеле 0.50

- 2-й актив ожидаемый доход 13%

с.к.о. ожидаемого дохода (риск) 20% отношение доход/риск = 0.65

234

минимальный вес в портфеле 0 максимальный вес в портфеле 0.50

- 3-й актив ожидаемый доход 18%

с.к.о. ожидаемого дохода (риск) 30% отношение доход/риск = 0.60 минимальный вес в портфеле 0 максимальный вес в портфеле 0.50 Коэффициенты корреляции между активами:

- 1-й и 2-й активы: р₁₂ = 0.5

- 1-й и 3-й активы: р₁₃ =-0.5

- 2-й и 3-й активы: р₂₃ = 0

Зададим минимально ожидаемый доход портфеля 15%, максимальный ожидаемый риск портфеля 18%, количество розыгрышей весов активов 10000.

Тогда решение задачи оптимизации по приведенному в этом параграфе алгоритму с выбором среди полученных решений того, которое обеспечивает максимальное отношение ожидаемого дохода к ожидаемому риску следующее:

- вес 1-го актива w₁ = 0.1141

- вес 2-го актива w₂ = 0.3859

- вес 3-го актива w₃ = 0.5000

- ожидаемый доход портфеля /и_у = 15.16%

- ожидаемый риск портфеля и _y = 16.58%

- отношение доход/риск = 0.91

Мы получили доход портфеля больше среднего арифметического доходов активов (13.67%), риск портфеля меньше среднего арифметического рисков активов (21.67%), и существенно улучшили соотношение дохода и риска по сравнению с этим соотношением для любого отдельного актива. Следует еще раз подчеркнуть, что это решение наверняка не является оптимальным. Более длинные серии розыгрышей вероятно способны его улучшить. Однако, данное решение является "достаточно оптимальным", так как удовлетворяет всем поставленным условиям.



Содержание раздела

---